Automorfismo - Automorphism
En matemáticas , un automorfismo es un isomorfismo de un objeto matemático a sí mismo. Es, en cierto sentido, una simetría del objeto y una forma de mapear el objeto a sí mismo mientras se conserva toda su estructura. El conjunto de todos los automorfismos de un objeto forma un grupo , llamado grupo de automorfismos . Es, en términos generales, el grupo de simetría del objeto.
Definición
En el contexto del álgebra abstracta , un objeto matemático es una estructura algebraica como un grupo , anillo o espacio vectorial . Un automorfismo es simplemente un homomorfismo biyectivo de un objeto consigo mismo. (La definición de homomorfismo depende del tipo de estructura algebraica; ver, por ejemplo, homomorfismo de grupo , homomorfismo de anillo y operador lineal ).
El morfismo de identidad ( mapeo de identidad ) se denomina automorfismo trivial en algunos contextos. Respectivamente, otros automorfismos (no identitarios) se denominan automorfismos no triviales .
La definición exacta de un automorfismo depende del tipo de "objeto matemático" en cuestión y qué, precisamente, constituye un "isomorfismo" de ese objeto. El escenario más general en el que estas palabras tienen significado es una rama abstracta de las matemáticas llamada teoría de categorías . La teoría de categorías se ocupa de objetos abstractos y morfismos entre esos objetos.
En la teoría de categorías, un automorfismo es un endomorfismo (es decir, un morfismo de un objeto a sí mismo) que también es un isomorfismo (en el sentido categórico de la palabra, lo que significa que existe un endomorfismo inverso de derecha e izquierda).
Esta es una definición muy abstracta ya que, en la teoría de categorías, los morfismos no son necesariamente funciones y los objetos no son necesariamente conjuntos. En la mayoría de los entornos concretos, sin embargo, los objetos serán conjuntos con alguna estructura adicional y los morfismos serán funciones que preserven esa estructura.
Grupo de automorfismo
Si los automorfismos de un objeto X forman un conjunto (en lugar de una clase adecuada ), entonces forman un grupo bajo la composición de morfismos . Este grupo se llama el grupo de automorfismos de X .
- Cierre
- La composición de dos automorfismos es otro automorfismo.
- Asociatividad
- Es parte de la definición de una categoría que la composición de los morfismos sea asociativa.
- Identidad
- La identidad es el morfismo identitario de un objeto a sí mismo, que es un automorfismo.
- Inversos
- Por definición, todo isomorfismo tiene un inverso que también es un isomorfismo, y dado que el inverso también es un endomorfismo del mismo objeto, es un automorfismo.
El grupo de automorfismo de un objeto X en una categoría C se denota Aut C ( X ), o simplemente Aut ( X ) si la categoría está clara por el contexto.
Ejemplos de
- En la teoría de conjuntos , una permutación arbitraria de los elementos de un conjunto X es un automorfismo. El grupo de automorfismos de X es también llamado el grupo simétrico en X .
- En aritmética elemental , el conjunto de enteros , Z , considerado como un grupo bajo la suma, tiene un automorfismo no trivial único: la negación. Sin embargo, considerado como un anillo, solo tiene el automorfismo trivial. En términos generales, la negación es un automorfismo de cualquier grupo abeliano , pero no de un anillo o campo.
- Un automorfismo de grupo es un isomorfismo de grupo de un grupo a sí mismo. De manera informal, es una permutación de los elementos del grupo de manera que la estructura permanece sin cambios. Para cada grupo G hay un homomorfismo natural Grupo G → Aut ( G ) cuya imagen es el grupo Inn ( G ) de automorfismos interiores y cuyo núcleo es el centro de G . Por lo tanto, si G tiene un centro trivial , puede integrarse en su propio grupo de automorfismos.
- En álgebra lineal , un endomorfismo de un espacio vectorial V es un operador lineal V → V . Un automorfismo es un operador lineal invertible en V . Cuando el espacio vectorial es de dimensión finita, el grupo de automorfismo de V es el mismo que el grupo lineal general , GL ( V ). (La estructura algebraica de todos los endomorfismos de V es en sí misma un álgebra sobre el mismo campo base que V , cuyos elementos invertibles consisten precisamente en GL ( V )).
- Un automorfismo de campo es un homomorfismo de anillo biyectivo de un campo a sí mismo. En los casos de los números racionales ( Q ) y los números reales ( R ) no hay automorfismos de campo no triviales. Algunos subcampos de R tienen automorfismos de campo no triviales, que sin embargo no se extienden a todo R (porque no pueden preservar la propiedad de un número que tiene una raíz cuadrada en R ). En el caso de los números complejos , C , hay un automorfismo no trivial único que envía R a R : conjugación compleja , pero hay infinitamente ( incontables ) muchos automorfismos "salvajes" (asumiendo el axioma de elección ). Los automorfismos de campo son importantes para la teoría de las extensiones de campo , en particular las extensiones de Galois . En el caso de una extensión de Galois L / K, el subgrupo de todos los automorfismos de L que fijan K puntualmente se denomina grupo de Galois de la extensión.
- El grupo de automorfismos de los cuaterniones ( H ) como anillo son los automorfismos internos, según el teorema de Skolem-Noether : mapas de la forma a ↦ bab -1 . Este grupo es isomorfo a SO (3) , el grupo de rotaciones en el espacio tridimensional.
- El grupo de automorfismo de los octoniones ( O ) es el excepcional grupo de Lie G 2 .
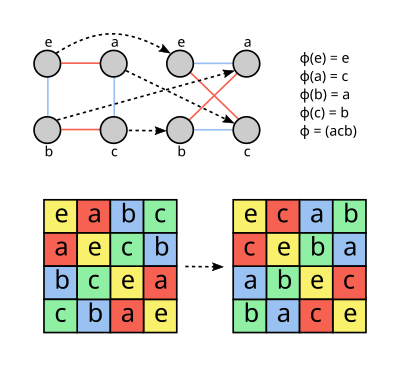
- En teoría de grafos, un automorfismo de un grafo es una permutación de los nodos que conserva los bordes y los no bordes. En particular, si dos nodos están unidos por un borde, también lo están sus imágenes bajo la permutación.
- En geometría , un automorfismo puede denominarse movimiento del espacio. También se utiliza terminología especializada:
- En geometría métrica, un automorfismo es una autoisometría . El grupo de automorfismo también se denomina grupo de isometría .
- En la categoría de superficies de Riemann , un automorfismo es un mapa biholomórfico (también llamado mapa conforme ), de una superficie a sí mismo. Por ejemplo, los automorfismos de la esfera de Riemann son transformaciones de Möbius .
- Un automorfismo de una variedad diferenciable M es un difeomorfismo de M a sí mismo. El grupo de automorfismo a veces se denomina Diff ( M ).
- En topología , los morfismos entre espacios topológicos se denominan mapas continuos , y un automorfismo de un espacio topológico es un homeomorfismo del espacio en sí mismo, o auto-homeomorfismo (ver grupo de homeomorfismo ). En este ejemplo, no es suficiente que un morfismo sea biyectivo para ser un isomorfismo.
Historia
Uno de los primeros automorfismos de grupo (automorfismo de un grupo, no simplemente un grupo de automorfismos de puntos) lo dio el matemático irlandés William Rowan Hamilton en 1856, en su cálculo icosiano , donde descubrió un automorfismo de orden dos, escribiendo:
de modo que esa es una nueva quinta raíz de unidad, conectada con la quinta raíz anterior por relaciones de perfecta reciprocidad.
Automorfismos internos y externos
En algunas categorías, en particular grupos , anillos y álgebras de Lie , es posible separar los automorfismos en dos tipos, llamados automorfismos "internos" y "externos".
En el caso de los grupos, los automorfismos internos son las conjugaciones de los elementos del propio grupo. Para cada elemento a de un grupo G , la conjugación de a es la operación φ a : G → G dada por φ a ( g ) = aga −1 (o a −1 ga ; el uso varía). Se puede comprobar fácilmente que la conjugación de a es un automorfismo de grupo. Los automorfismos internos forman un subgrupo normal de Aut ( G ), denotado por Inn ( G ); esto se llama lema de Goursat .
Los otros automorfismos se denominan automorfismos externos . El grupo de cocientes Aut ( G ) / Inn ( G ) generalmente se denota por Out ( G ); los elementos no triviales son las clases laterales que contienen los automorfismos externos.
La misma definición se aplica a cualquier anillo unital o álgebra donde a es cualquier elemento invertible . Para las álgebras de Lie, la definición es ligeramente diferente.
Ver también
- Antiautomorfismo
- Automorfismo (en rompecabezas de Sudoku)
- Subgrupo característico
- Anillo de endomorfismo
- Automorfismo de Frobenius
- Morfismo
- Automorfismo de órdenes (en teoría de órdenes ).
- Automorfismo que preserva la relación
- Transformada fraccional de Fourier
Referencias
- ^ PJ Pahl, R Damrath (2001). "§7.5.5 Automorfismos" . Fundamentos matemáticos de la ingeniería computacional (traducción de Felix Pahl ed.). Saltador. pag. 376. ISBN 3-540-67995-2.
- ^ Yale, Paul B. (mayo de 1966). "Automorfismos de los números complejos" (PDF) . Revista de Matemáticas . 39 (3): 135-141. doi : 10.2307 / 2689301 . JSTOR 2689301 .
- ^ Lounesto, Pertti (2001), Clifford Algebras and Spinors (2ª ed.), Cambridge University Press, págs. 22-23, ISBN 0-521-00551-5
- ^ Manual de álgebra , 3 , Elsevier , 2003, p. 453
- ^ Sir William Rowan Hamilton (1856). "Memorándum respetando un nuevo Sistema de Raíces de Unidad" (PDF) . Revista filosófica . 12 : 446.


