Matemáticas del Sudoku - Mathematics of Sudoku

Un Sudoku automórfico de 24 pistas con simetría de traslación

Los rompecabezas de Sudoku se pueden estudiar matemáticamente para responder preguntas como "¿Cuántas cuadrículas de Sudoku llenas hay?" , " ¿Cuál es el número mínimo de pistas en un acertijo válido? " Y "¿De qué manera pueden ser simétricas las cuadrículas de Sudoku?" mediante el uso de combinatoria y teoría de grupos .

Los principales resultados son que para el Sudoku clásico el número de cuadrículas llenas es 6.670.903.752.021.072.936.960 (6,67 × 10 ²¹ ), que se reduce a 5,472,730,538 grupos esencialmente diferentes bajo las transformaciones de preservación de validez . Hay 26 tipos de simetría, pero solo se pueden encontrar en aproximadamente el 0,005% de todas las cuadrículas llenas. Un rompecabezas con una solución única debe tener al menos 17 pistas, y hay un rompecabezas que se puede resolver con un máximo de 21 pistas por cada cuadrícula resuelta. El rompecabezas mínimo más grande encontrado hasta ahora tiene 40 pistas.

Se conocen resultados similares para variantes y cuadrículas más pequeñas. No se conocen resultados exactos para Sudokus más grandes que la cuadrícula clásica de 9 × 9, aunque hay estimaciones que se cree que son bastante precisas.

Visión general

El análisis de Sudoku se divide en dos áreas principales:

analizar las propiedades de las rejillas completadas
analizar las propiedades de los rompecabezas completados.

El análisis inicial se centró principalmente en enumerar soluciones, y los resultados aparecieron por primera vez en 2004.

Hay muchas variantes de Sudoku , caracterizadas parcialmente por el tamaño ( N ) y la forma de sus regiones . A menos que se indique lo contrario, la discusión en este artículo asume el Sudoku clásico, es decir, N = 9 (una cuadrícula de 9 × 9 y regiones de 3 × 3). A Sudoku rectangular utiliza regiones rectangulares de fila-columna dimensión R × C . Otras variantes incluyen aquellas con regiones de forma irregular o con restricciones adicionales ( hipercubo ) o diferentes tipos de restricciones ( Samunamupure ).

Las regiones también se denominan bloques o cajas . Una banda es una parte de la cuadrícula que encapsula 3 filas y 3 cajas, y una pila es una parte de la cuadrícula que encapsula 3 columnas y 3 cajas. Un rompecabezas es una cuadrícula parcialmente completada , y los valores iniciales son dados o pistas . Un acertijo adecuado tiene una solución única. Un acertijo mínimo es un acertijo adecuado del que no se puede eliminar ninguna pista sin introducir soluciones adicionales. Consulte el Glosario de Sudoku para obtener más terminología.

La resolución de Sudokus desde el punto de vista de un jugador se ha explorado en el libro de Denis Berthier "La lógica oculta del Sudoku" (2007), que considera estrategias como "cadenas xy ocultas".

Contexto matemático

Se sabe que el problema general de resolver rompecabezas de Sudoku en n ² × n ² cuadrículas de n × n bloques es NP-completo . Para n = 3 (Sudoku clásico), sin embargo, este resultado es de poca relevancia práctica: los algoritmos pueden resolver acertijos en una fracción de segundo debido al pequeño tamaño del problema.

Un rompecabezas se puede expresar como un problema de coloración de gráficos . El objetivo es construir una coloración 9 de un gráfico particular, dada una coloración 9 parcial. El gráfico de Sudoku tiene 81 vértices, un vértice para cada celda. Los vértices están etiquetados con pares ordenados ( x , Y ), donde x y y son enteros entre 1 y 9. En este caso, dos vértices distintos etiquetados por ( x , y ) y ( x ', y ') están unidos por una borde si y solo si :

x = x ′ (misma columna) o,
y = y ′ (misma fila) o,
⌈ x / 3 ⌉ = ⌈ x ′ / 3 ⌉ y ⌈ y / 3 ⌉ = ⌈ y ′ / 3 ⌉ (la misma celda de 3 × 3)

El rompecabezas se completa luego asignando un número entero entre 1 y 9 a cada vértice, de tal manera que los vértices que están unidos por una arista no tengan asignado el mismo número entero.

Una cuadrícula de solución de Sudoku también es un cuadrado latino . Hay significativamente menos cuadrículas de Sudoku que cuadrados latinos porque Sudoku impone la restricción regional adicional.

Sudokus de tablas de grupo

Como en el caso de los cuadrados latinos, las tablas de (suma o) multiplicación ( tablas de Cayley ) de grupos finitos pueden usarse para construir Sudokus y tablas de números relacionadas. Es decir, hay que tener en cuenta los subgrupos y los grupos de cocientes :

Tomemos, por ejemplo, el grupo de pares, agregando cada componente por separado módulo algunos . Al omitir uno de los componentes, de repente nos encontramos (y este mapeo es obviamente compatible con las respectivas adiciones, es decir, es un homomorfismo de grupo ). También se dice que el último es un grupo cociente del primero, porque algunos elementos que alguna vez fueron diferentes se vuelven iguales en el nuevo grupo. Sin embargo, también es un subgrupo, porque simplemente podemos llenar el componente que falta para volver . ${\ Displaystyle \ mathbb {Z} _ {n} \ oplus \ mathbb {Z} _ {n}}$ ${\ Displaystyle n}$ ${\ Displaystyle \ mathbb {Z} _ {n}}$ ${\ Displaystyle 0}$ ${\ Displaystyle \ mathbb {Z} _ {n} \ oplus \ mathbb {Z} _ {n}}$

Bajo esta vista, escribimos el ejemplo, Cuadrícula 1 , para . ${\ Displaystyle n = 3}$

Cada región de Sudoku se ve igual en el segundo componente (es decir, como el subgrupo ), porque estos se agregan independientemente del primero. Por otro lado, los primeros componentes son iguales en cada bloque, y si imaginamos cada bloque como una celda, estos primeros componentes muestran el mismo patrón (es decir, el grupo de cocientes ). Como se describe en el artículo de cuadrados latinos, este es un cuadrado latino de orden . ${\ Displaystyle \ mathbb {Z} _ {3}}$ ${\ Displaystyle \ mathbb {Z} _ {3}}$ ${\ Displaystyle 9}$

Ahora, para producir un Sudoku, permítenos permutar las filas (o equivalentemente las columnas) de tal manera que cada bloque se redistribuya exactamente una vez en cada bloque, por ejemplo, ordenarlos . Esto, por supuesto, conserva la propiedad de la plaza latina. Además, en cada bloque, las líneas tienen un primer componente distinto por construcción y cada línea en un bloque tiene entradas distintas a través del segundo componente, porque los segundos componentes de los bloques originalmente formaban un cuadrado latino de orden (del subgrupo ). Así llegamos a un Sudoku (cambie el nombre de los pares a los números 1 ... 9 si lo desea). Con el ejemplo y la permutación de filas de arriba, llegamos a la Cuadrícula 2 . ${\ Displaystyle 1,4,7,2,5,8,3,6,9}$ ${\ Displaystyle 3}$ ${\ Displaystyle \ mathbb {Z} _ {3}}$

Cuadrícula 1 : la tabla de suma en

{\ Displaystyle \ mathbb {Z} _ {3} \ oplus \ mathbb {Z} _ {3}}

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

Grid 2 - Generando un Sudoku

(0,0)	(0,1)	(0,2)
(1,0)	(1,1)	(1,2)
(2,0)	(2,1)	(2,2)

(1,0)	(1,1)	(1,2)
(2,0)	(2,1)	(2,2)
(0,0)	(0,1)	(0,2)

(2,0)	(2,1)	(2,2)
(0,0)	(0,1)	(0,2)
(1,0)	(1,1)	(1,2)

(0,1)	(0,2)	(0,0)
(1,1)	(1,2)	(1,0)
(2,1)	(2,2)	(2,0)

(1,1)	(1,2)	(1,0)
(2,1)	(2,2)	(2,0)
(0,1)	(0,2)	(0,0)

(2,1)	(2,2)	(2,0)
(0,1)	(0,2)	(0,0)
(1,1)	(1,2)	(1,0)

(0,2)	(0,0)	(0,1)
(1,2)	(1,0)	(1,1)
(2,2)	(2,0)	(2,1)

(1,2)	(1,0)	(1,1)
(2,2)	(2,0)	(2,1)
(0,2)	(0,0)	(0,1)

(2,2)	(2,0)	(2,1)
(0,2)	(0,0)	(0,1)
(1,2)	(1,0)	(1,1)

Para que este método funcione, generalmente no se necesita un producto de dos grupos del mismo tamaño. Una llamada secuencia corta exacta de grupos finitos de tamaño apropiado ya hace el trabajo. Pruebe, por ejemplo, el grupo con cociente y subgrupo . Parece claro (ya a partir de los argumentos de enumeración) que no todos los Sudokus se pueden generar de esta manera. ${\ Displaystyle \ mathbb {Z} _ {4}}$ ${\ Displaystyle \ mathbb {Z} _ {2}}$

Variantes

Un Sudoku se puede interpretar como un mosaico (o cubierta ) de un cuadrado latino con poliominós (las regiones del Sudoku). El clásico Sudoku 9 × 9 está hecho de nonominoes cuadrados . Es posible aplicar las reglas del Sudoku a rompecabezas de otros tamaños, aunque solo los Sudoku N ² × N ² se pueden enlosar con poliominós cuadrados.

Consulte el Glosario de Sudoku para obtener una lista ampliada de variantes.

Regiones rectangulares

Una variante popular está hecha de regiones rectangulares ( bloques o cajas ), por ejemplo, hexominós de 2 × 3 en mosaico en una cuadrícula de 6 × 6. La siguiente notación se utiliza para discutir esta variante:

R × C denota una región rectangular con R filas y C columnas.
La configuración de cuadrícula implícita tiene:
- dimensiones de la cuadrícula N × N , donde N = R × C
- N bloques ( cajas ) de tamaño R × C , dispuestos en una 'superrejilla' C × R
- Bandas C de tamaño R × N , formadas por R bloques adyacentes horizontalmente
- R pilas de tamaño N × C , que constan de C bloques adyacentes verticalmente

Los sudoku con regiones cuadradas N × N son más simétricos que los sudoku rectangulares, ya que cada fila y columna cruza N regiones y comparte N celdas con cada una. El número de bandas y las pilas es también igual a N . El Sudoku "3 × 3" es además único: N es también el número de restricciones de fila-columna-región de la Regla Única (es decir, hay N = 3 tipos de unidades ).

Sudokus de rompecabezas

Un Sudoku cuyas regiones no son (necesariamente) cuadradas o rectangulares se conoce como Jigsaw Sudoku. En particular, un cuadrado N × N donde N es primo solo se puede colocar en mosaico con N -ominós irregulares . Para valores pequeños de N, se ha calculado el número de formas de enlosar el cuadrado (excluidas las simetrías) (secuencia A172477 en la OEIS ). Para N ≥ 4, algunas de estas teselaciones no son compatibles con ningún cuadrado latino; es decir, todos los rompecabezas de Sudoku en un mosaico de este tipo no tienen solución.

Soluciones

La respuesta a la pregunta "¿Cuántas cuadrículas de Sudoku hay?" depende de la definición de cuándo se consideran diferentes soluciones similares.

Sudoku ordinario

Todas las soluciones

Para la enumeración de todas las soluciones posibles, dos soluciones se consideran distintas si alguno de sus valores de celda correspondientes (81) difiere. Se ignoran las relaciones de simetría entre soluciones similares, por ejemplo, las rotaciones de una solución se consideran distintas. Las simetrías juegan un papel importante en la estrategia de enumeración, pero no en el recuento de todas las posibles soluciones.

La primera solución conocida para completar la enumeración fue publicada por QSCGZ (Guenter Stertenbrink) en el grupo de noticias rec.puzzles en 2003, obteniendo 6,670,903,752,021,072,936,960 (6,67 × 10 ²¹ ) soluciones distintas.

En un estudio de 2005, Felgenhauer y Jarvis analizaron las permutaciones de la banda superior utilizadas en soluciones válidas. Una vez que se identificaron las simetrías Band1 y las clases de equivalencia para las soluciones de cuadrícula parcial, se construyeron las terminaciones de las dos bandas inferiores y se contaron para cada clase de equivalencia. Sumando las terminaciones sobre las clases de equivalencia, ponderadas por el tamaño de la clase, da el número total de soluciones como 6,670,903,752,021,072,936,960, lo que confirma el valor obtenido por QSCGZ. Posteriormente, el valor se confirmó varias veces de forma independiente. Posteriormente se desarrolló una segunda técnica de enumeración basada en la generación de bandas que es significativamente menos intensiva desde el punto de vista informático. Esta técnica posterior resultó en la necesidad de aproximadamente 1/97 de la cantidad de ciclos de cálculo que las técnicas originales, pero fue significativamente más complicada de configurar.

Soluciones esencialmente diferentes

Transformaciones que preservan la validez

Dos cuadrículas válidas son esencialmente lo mismo si una se puede derivar de la otra, utilizando la denominada transformación de preservación de validez (VPT) . Estas transformaciones siempre transforman una cuadrícula válida en otra cuadrícula válida. Hay dos tipos principales: permutaciones de símbolos (reetiquetado) y permutaciones de celda (reordenamientos). Son:

Reetiquetado de símbolos (¡9!)
(Una vez que se eliminan todas las posibles combinaciones de reetiquetado, excepto una: por ejemplo, manteniendo la fila superior fija en [123456789], el número de cuadrículas fijas se reduce a 18,383,222,420,692,992. ¡Este valor es 6,670,903,752,021,072,936,960 dividido por 9!)

y reorganizar (barajar):

Permutaciones de banda (¡3!)
Permutaciones de filas dentro de una banda (¡3! × 3! × 3!)
Permutaciones de pila (¡3!)
Permutaciones de columna dentro de una pila (¡3! × 3! × 3!)
Reflexión, transposición y rotación (2)
(Dada una sola transposición o rotación de un cuarto de vuelta junto con las permutaciones anteriores, se puede producir cualquier combinación de reflexiones, transposiciones y rotaciones, por lo que estas operaciones solo contribuyen con un factor de 2)

Estas operaciones definen una relación entre cuadrículas equivalentes. Con respecto a los 81 valores de celda de la cuadrícula, las operaciones de reordenamiento forman un subgrupo del grupo simétrico S ₈₁ , de orden 3! ⁸ × 2 = 3.359.232 Las operaciones de reetiquetado son isomorfas con S ₉ y generan un 9 adicional. = 362,880 cuadrículas equivalentes. La aplicación de estas operaciones en una cuadrícula da como resultado 3! ⁸ × 2 × 9! o 1.218.998.108.160 rejillas esencialmente equivalentes. Sin embargo, hay una pequeña cantidad de sudokus para los cuales las operaciones anteriores generan menos cuadrículas; estos son los sudokus auto-similares o automórficos . Solo alrededor del 0.01% de todas las cuadrículas esencialmente únicas son automórficas, pero contarlas es necesario para evaluar el número exacto de sudokus esencialmente diferentes.

El grupo de simetría del sudoku

La estructura precisa del grupo de simetría del sudoku se puede expresar de forma sucinta utilizando el producto de corona (≀). ¡Las posibles permutaciones de filas (o columnas) forman un grupo isomorfo a S ₃ ≀ S ₃ de orden 3! ⁴ = 1.296. Todo el grupo de reordenamiento se forma dejando que la operación de transposición (isomórfica a C ₂ ) actúe sobre dos copias de ese grupo, una para las permutaciones de fila y otra para las permutaciones de columna. Este es S ₃ ≀ S ₃ ≀ C ₂ , un grupo de orden 1.296 ² × 2 = 3.359.232. Finalmente, las operaciones de reetiquetado se conmutan con las operaciones de reordenamiento, por lo que el grupo completo de sudoku (VPT) es ( S ₃ ≀ S ₃ ≀ C ₂ ) × S ₉ de orden 1.218.998.108.160.

Puntos fijos y lema de Burnside

El conjunto de cuadrículas equivalentes al que se puede llegar utilizando estas operaciones (excluyendo el reetiquetado) forma una órbita de cuadrículas bajo la acción del grupo de reordenamiento . El número de soluciones esencialmente diferentes es entonces el número de órbitas, que se puede calcular utilizando el lema de Burnside . Los puntos fijos de Burnside son cuadrículas que no cambian bajo la operación de reordenamiento o solo se diferencian por el reetiquetado. Para simplificar el cálculo, los elementos del grupo de reordenamiento se clasifican en clases de conjugación , cuyos elementos tienen todos el mismo número de puntos fijos. Resulta que sólo 27 de las 275 clases de conjugación del grupo de reordenamiento tienen puntos fijos; estas clases de conjugación representan los diferentes tipos de simetría (auto-semejanza o automorfismo) que se pueden encontrar en cuadrículas de sudoku completadas. Usando esta técnica, Ed Russell y Frazer Jarvis fueron los primeros en calcular el número de soluciones de sudoku esencialmente diferentes como 5.472.730.538 .

Clases conjugadas del grupo de reordenamiento con puntos fijos ("automorfismos" y su prevalencia)
Nombre o composición	Código	Id de clase	Tamaño de la clase	Ciclos celulares	O	F	Número de rejillas fijas (hasta reetiquetado), por elemento	Número de rejillas fijas, por elemento	Número de rejillas fijas (hasta reetiquetado), toda la clase	Número de rejillas fijas, toda la clase
Identidad	mi	1	1		1	81	18,383,222,420,692,992	6,670,903,752,021,072,936,960	18,383,222,420,692,992	6,670,903,752,021,072,936,960
Mini filas (MR)	ccc	8	dieciséis	27 × 3	3	0	107,495,424	39,007,939,461,120	1,719,926,784	624,127,031,377,920
2 MR, 1 MD	ccc \| C	7	96	27 × 3	3	0	21,233,664	7.705.271.992.320	2,038,431,744	739,706,111,262,720
1 señor, 2 médicos	ccc \| cc	9	192	27 × 3	3	0	4.204.224	1,525,628,805,120	807,211,008	292,920,730,583,040
Mini diagonales (MD)	ccc \| ccc	10	64	27 × 3	3	0	2.508.084	910,133,521,920	160,517,376	58,248,545,402,880
Saltar filas (JR)	C	25	144	27 × 3	3	0	14,837,760	5.384.326.348.800	2,136,637,440	775,342,994,227,200
2 JR, 1 GR	C \| C	28	864	27 × 3	3	0	2,085,120	756,648,345,600	1,801,543,680	653,744,170,598,400
1 JR, 2 GR	C \| cc	30	1,728	27 × 3	3	0	294,912	107,017,666,560	509,607,936	184,926,527,815,680
Filas deslizantes (GR)	C \| ccc	32	1,152	27 × 3	3	0	6.342.480	2.301.559.142.400	7,306,536,960	2.651.396.132.044.800
Filas completas (FR)	C9	27	288	9 × 9	9	0	5.184	1,881,169,920	1,492,992	541,776,936,960
2 FR, 1 WR	C9 \| C	26	1,728	9 × 9	9	0	2.592	940,584,960	4.478.976	1,625,330,810,880
1 FR, 2 WR	C9 \| cc	29	3.456	9 × 9	9	0	1.296	470,292,480	4.478.976	1,625,330,810,880
Filas onduladas (WR)	C9 \| ccc	31	2.304	9 × 9	9	0	648	235,146,240	1,492,992	541,776,936,960
Saltar diagonales (JD)	C \| C	22	5.184	27 × 3	3	0	323,928	117,546,992,640	1,679,242,752	609,363,609,845,760
Columnas rotas (BC)	C \| C9	24	20,736	9 × 9	9	0	288	104,509,440	5.971.968	2,167,107,747,840
Diagonales completas (FD)	C9 \| C9	23	20,736	9 × 9	9	0	162	58,786,560	3.359.232	1.218.998.108.160
Espejo diagonal (DM)	T	37	1.296	36 × 2	2	9	30,258,432	10,980,179,804,160	39,214,927,872	14,230,313,026,191,360
DM + MD	T ccc	40	10,368	3 × 3, 12 × 6	6	0	1.854	672,779,520	19,222,272	6,975,378,063,360
DM + JD	TC	43	93,312	3 × 3, 12 × 6	6	0	288	104,509,440	26,873,856	9,751,984,865,280
Cuarto de vuelta (QT)	T sS	86	69,984	20 × 4	4	1	13,056	4.737.761.280	913,711,104	331,567,485,419,520
Media vuelta (HT)	sS \| sS	79	2,916	40 × 2	2	1	155,492,352	56,425,064,693,760	453,415,698,432	164,535,488,647,004,160
Palos de columna (CS)	S \| sss	134	972	36 × 2	2	9	449,445,888	163,094,923,837,440	436,861,403,136	158,528,265,969,991,680
CS + MC	cS6 \| sss	135	3.888	3 × 3, 12 × 6	6	0	27,648	10.032.906.240	107,495,424	39,007,939,461,120
CS + GR	cS6 \| C6	142	31,104	3 × 3, 12 × 6	6	0	6.480	2,351,462,400	201,553,920	73,139,886,489,600
CS + JR / B2, GR / B13	S6 \| C6	143	15,552	3 × 3, 12 × 6	6	0	1,728	627,056,640	26,873,856	9,751,984,865,280
CS + GR / Band2, JR / B13	cS \| C6	144	15,552	3 × 3, 12 × 6	6	0	3.456	1.254.113.280	53,747,712	19,503,969,730,560
CS + JR	S \| C6	145	7.776	3 × 3, 12 × 6	6	0	13,824	5,016,453,120	107,495,424	39,007,939,461,120
(no trivial)									949,129,933,824	344,420,270,386,053,120
total									18,384,171,550,626,816	6,671,248,172,291,458,990,080

Tenga en cuenta que una cuadrícula puede ser un punto fijo de varias transformaciones simultáneamente; por ejemplo, cualquier cuadrícula que tenga una simetría de cuarto de vuelta también tiene simetría de media vuelta. La combinación de todas las transformaciones que fijan una cuadrícula en particular es el subgrupo estabilizador ("grupo de automorfismo") de esa cuadrícula.

Subgrupos de estabilizadores

Russell ha compilado una lista de 122 clases de conjugación de subgrupos de estabilizadores no triviales "esencialmente diferentes" ("grupos de automorfismo"), junto con una cuadrícula de ejemplo, las clases de conjugación de VPT en el grupo, un conjunto de generadores y el número de cuadrículas esencialmente diferentes. (órbitas) con esa clase de estabilizador. Hasta el isomorfismo hay 26 estructuras de grupos diferentes. Hay 15 tamaños diferentes de grupos de estabilizadores posibles, que se enumeran en la siguiente sección.

Número de cuadrículas esencialmente equivalentes

Cada una de las cuadrículas esencialmente únicas se puede analizar en busca de auto-similitudes ("automorfismos") para evaluar la "deficiencia" en el número de cuadrículas esencialmente equivalentes. Los resultados están resumidos en la tabla que se encuentra abajo. En total, 560,151 de las 5,472,730,538 cuadrículas esencialmente únicas (aproximadamente 1 / 10,000) tienen una forma de auto-similitud (un estabilizador no trivial).

El tamaño de la órbita (es decir, el número de cuadrículas esencialmente equivalentes) se puede calcular utilizando el teorema del estabilizador de órbita : es el tamaño del grupo de simetría del sudoku dividido por el tamaño del grupo estabilizador (o "automorfismo"). Multiplicar el número de cuadrículas esencialmente únicas (el número de órbitas) por el tamaño de la órbita da el número total de cuadrículas con ese tamaño de grupo estabilizador; La suma proporciona una vez más el número total de posibles cuadrículas de sudoku. Las cuadrículas "automórficas" tienen órbitas más pequeñas, por lo que la probabilidad de que una cuadrícula aleatoria tenga una simetría desciende: de aproximadamente 1 en 10.000 para cuadrículas esencialmente diferentes a aproximadamente 1 en 20.000 para todas las cuadrículas.

Número de cuadrículas de sudoku por tamaño de grupo de estabilizadores
Tamaño del grupo estabilizador	No. de cuadrículas esencialmente únicas (número de órbitas)	Cuadrículas equivalentes (tamaño de la órbita), ignorando el reetiquetado	Número de cuadrículas, ignorando el reetiquetado	Cuadrículas equivalentes (tamaño de la órbita), incluido el reetiquetado	Número total de cuadrículas
1	5.472.170.387	3.359.232	18,382,289,873,462,784	1.218.998.108.160	6,670,565,349,282,175,057,920
2	548,449	1,679,616	921.183.715.584	609,499,054,080	334,279,146,711,121,920
3	7.336	1,119,744	8.214.441.984	406,332,702,720	2,980,856,707,153,920
4	2.826	839,808	2,373,297,408	304,749,527,040	861,222,163,415,040
6	1,257	559,872	703,759,104	203,166,351,360	255,380,103,659,520
8	29	419,904	12,177,216	152,374,763,520	4.418.868.142.080
9	42	373,248	15,676,416	135,444,234,240	5,688,657,838,080
12	92	279,936	25,754,112	101,583,175,680	9.345.652.162.560
18	85	186,624	15,863,040	67,722,117,120	5.756.379.955.200
27	2	124,416	248,832	45.148.078.080	90,296,156,160
36	15	93,312	1.399.680	33,861,058,560	507,915,878,400
54	11	62,208	684,288	22,574,039,040	248,314,429,440
72	2	46,656	93,312	16,930,529,280	33,861,058,560
108	3	31,104	93,312	11,287,019,520	33,861,058,560
162	1	20,736	20,736	7.524.679.680	7.524.679.680
648	1	5.184	5.184	1,881,169,920	1,881,169,920
> 1	560,151		932,547,230,208		338,402,738,897,879,040
	5.472.730.538		18,383,222,420,692,992		6,670,903,752,021,072,936,960

Otras variantes

Se han calculado los resultados de la enumeración para muchas variantes de Sudoku: estos se resumen a continuación.

Sudoku con restricciones adicionales

Las siguientes son todas las restricciones del clásico Sudoku 3 × 3 (cuadrícula de 9 × 9). Los nombres de los tipos no se han estandarizado: haga clic en los enlaces de atribución para ver las definiciones.

Escribe	Numero de rejillas	Atribución	Verificado?
Sudoku cuasi-mágico	248,832	Jones, Perkins y Roach	sí
Sudoku mágico	5.971.968	Stertenbrink	sí
Hipercubo	37,739,520	Stertenbrink	sí
3doku	104,015,259,648	Stertenbrink	sí
Sudoku NRC	6.337.174.388.428.800	Brouwer	sí
Sudoku X	55,613,393,399,531,520	Russell	sí
Grupos disjuntos	201,105,135,151,764,480	Russell	sí

Sudoku con regiones rectangulares

En la tabla, las dimensiones de los bloques son las de las regiones (por ejemplo, 3 × 3 en el Sudoku normal). La columna "Rel Err" indica cómo se compara una aproximación simple basada en los recuentos de bandas calculados (que se detallan en las secciones siguientes) con el recuento de cuadrícula real: es una subestimación en todos los casos evaluados hasta ahora. Los números para cuadrículas de bloques cuadrados ( n ² × n ² ) se enumeran en (secuencia A107739 en la OEIS ), y los números para 2 × n bloques (2 n × 2 n cuadrículas) se enumeran en (secuencia A291187 en la OEIS ) .

De manera similar a los cuadrados latinos , el número de cuadrículas de sudoku se puede reducir notando que hay una correspondencia uno a uno con una forma parcialmente estandarizada, en la que el primer bloque tiene las etiquetas canónicas y tanto la fila superior como la columna más a la izquierda están ordenadas (tanto como lo permitan las reglas, es decir, dentro de los bloques y las propias pilas / bandas). Para una cuadrícula con bloques, cada cuadrícula reducida corresponde a ${\ Displaystyle R \ times C}$

{\ Displaystyle (RC)! \ times (R!) ^ {C-1} (C-1)! \ times (C!) ^ {R-1} (R-1)! = (RC-1)! \ cdot R! ^ {C} \ cdot C! ^ {R}}

cuadrículas totales, que es 9! × 72 ² o 1.881.169.920 para el Sudoku 3 × 3 normal. Esta reducción es siempre uno a uno, a diferencia de la acción del conjunto completo de transformaciones que preservan la validez ('simetrías Sudoku') que se analizan a continuación.

Dimensiones		Número de cuadrículas completas				Est. error (vea abajo)	Fracción de Cuadrados latinos
Red	Bloques	Exacto	Magnitud	Atribución	Verificado?	Est. error (vea abajo)	Fracción de Cuadrados latinos
4 × 4	2 × 2	288	2.8800 × 10 ²	varios	sí	−11,1%	0,5 × 10 ⁰
6 × 6	2 × 3	28,200,960	2.8201 × 10 ⁷	Pettersen	sí	−5,88%	3,5 × 10 ⁻²
8 × 8	2 × 4	29,136,487,207,403,520	2.9136 × 10 ¹⁶	Russell	sí	−1,91%	2,7 × 10 ⁻⁴
9 × 9	3 × 3	6,670,903,752,021,072,936,960	6.6709 × 10 ²¹	Stertenbrink	sí	−0,207%	1,2 × 10 ⁻⁶
10 × 10	2 × 5	1.903.816.047.972.624.930.994.913.280.000	1,9038 × 10 ³⁰	Pettersen	sí	−0,375%	1,9 × 10 ⁻⁷
12 × 12	3 × 4	81,171,437,193,104,932,746,936,103,027,318,645,818,654,720,000	8.1171 × 10 ⁴⁶	Pettersen / Plata	No	−0,132%	desconocido
12 × 12	2 × 6	38,296,278,920,738,107,863,746,324,732,012,492,486,187,417,600,000	3.8296 × 10 ⁴⁹	Pettersen	No	−0,238%	desconocido
15 × 15	3 × 5	desconocido	est. 3.5086 × 10 ⁸⁴	Plata	No	n / A	desconocido
16 × 16	4 × 4	desconocido	est. 5.9584 × 10 ⁹⁸	Plata	No	n / A	desconocido
20 × 20	4 × 5	desconocido	est. 3,1764 × 10 ¹⁷⁵	Plata	No	n / A	desconocido
25 × 25	5 × 5	desconocido	est. 4.3648 × 10 ³⁰⁸	Plata / Pettersen	No	n / A	desconocido

Un Sudoku resuelto seguirá siendo válido bajo las acciones de las transformaciones que preservan la validez (ver también Jarvis). Contando cuidadosamente el número de cuadrículas invariantes para cada transformación, se puede calcular el número de cuadrículas de Sudoku esencialmente diferentes (ver arriba). Se han aplicado métodos similares a las cuadrículas de sudoku de otras dimensiones; Los resultados están resumidos en la tabla que se encuentra abajo. Para cuadrículas de bloques cuadrados (secuencia A109741 en la OEIS ), la transformación de transposición puede o no estar incluida (ver más abajo) en el grupo VPT (simetría). El número de cuadrículas esencialmente diferentes se puede estimar dividiendo el número total de cuadrículas (conocidas o estimadas) por el tamaño del grupo VPT (que se calcula fácilmente), que esencialmente asume que el número de sudokus automórficos es insignificante. Los números para 2 × n bloques (2 n × 2 n cuadrículas) se enumeran en (secuencia A291188 en la OEIS ).

Dimensiones		Grupo VPT			Número de cuadrículas esencialmente diferentes	Referencia
Red	Bloques	T	Tamaño	Conj. clases (sin reetiquetado)	Número de cuadrículas esencialmente diferentes	Referencia
4 × 4	2 × 2	sí	128 × 4!		2
4 × 4	2 × 2	no	64 × 4!		3
6 × 6	2 × 3	no	¡3.456 × 6!	90	49	Jarvis / Russell, Pettersen
8 × 8	2 × 4	no	4.423.368 × 8!	400	1,673,187	Russell, Pettersen
9 × 9	3 × 3	sí	¡3.359.232 × 9!	275	5.472.730.538	Jarvis / Russell, Pettersen
9 × 9	3 × 3	no	1.679.616 × 9!	484	10,945,437,157	Jarvis / Russell, Pettersen
10 × 10	2 × 5	no	110.592.000 × 10!	1260	4.743.933.602.050.718	Pettersen / Russell
16 × 16	4 × 4	sí	(¡4!) ¡ ¹⁰ × 2 × 16!		est. 2.2458 × 10 ⁷¹	(estimación explicada en texto)
16 × 16	4 × 4	no	(¡4!) ¡ ¹⁰ × 16!		est. 4.4916 × 10 ⁷¹	(estimación explicada en texto)

Método de estimación

El método de Kevin Kilfoil (generalizado por Pettersen) se puede utilizar para estimar el número de cuadrículas completadas utilizando el número de posibles bandas y pilas completadas. El método afirma que las restricciones de fila y columna del Sudoku son, en primera aproximación, condicionalmente independientes dada la restricción de caja. Esto le da a la fórmula Kilfoil-Silver-Pettersen :

{\ displaystyle {\ mbox {Número de cuadrículas RC × RC con cuadros R × C}} \ simeq {\ frac {(b_ {R, C}) ^ {C} \ times (b_ {C, R}) ^ { R}} {(RC)! ^ {RC}}}}

donde es el número de maneras de llenar un R × RC banda de R horizontalmente adyacente R × C cajas (de forma equivalente, es el número de maneras de llenar un RC × C pila de C adyacentes verticalmente R × C cajas), y el denominador ( RC )! ^RC es el número de formas de llenar la cuadrícula mientras se satisfacen solo las restricciones de la caja. ${\ Displaystyle b_ {R, C}}$ ${\ Displaystyle b_ {C, R}}$

Como explica Pettersen: "Así es como: Sea $X$ el espacio de las cuadrículas construidas por bandas de sudoku legales, pero sin prestar atención a si las columnas siguen las reglas del Sudoku. El tamaño de $X$ es . Sea $Y$ también el conjunto de cuadrículas construidas por pilas legales sin atención puesta en las filas, $#Y$ es entonces . Las cuadrículas nxm-sudoku son entonces la intersección de $X$ e $Y.$ Un aleatorio y son idénticas en un cuadro dado con probabilidad , y bajo el supuesto que estas probabilidades son independientes para cada casilla, llegamos a la estimación anterior ". ${\ Displaystyle (nm) \ times (nm)}$ ${\ Displaystyle b (n, m) ^ {m}}$ ${\ Displaystyle b (m, n) ^ {n}}$ ${\ Displaystyle x (\ in X)}$ ${\ Displaystyle y (\ in Y)}$ ${\ Displaystyle (nm)!}$

Esta estimación ha demostrado tener una precisión de aproximadamente 0,2% para la cuadrícula clásica de 9 × 9, y dentro del 1% para cuadrículas más grandes para las que se conocen valores exactos (consulte la tabla anterior).

Numero de bandas

Se conocen fórmulas exactas para el número de bandas posibles en una cuadrícula de sudoku llena con bloques de tamaño R × C : ${\ Displaystyle b_ {R, C}}$

Dimensiones		Numero de bandas	Atribución	Verificado?
Banda	Bloques	Numero de bandas	Atribución	Verificado?
2 × 2 C	2 × C	${\ Displaystyle b_ {2, C} = (2C)! (C!) ^ {2}}$	(resultado obvio)	sí
3 × 3 C	3 × C	${\ displaystyle b_ {3, C} = (3C)! (C!) ^ {6} \ sum _ {k = 0} ^ {C} {C \ elige k} ^ {3}}$ donde la suma se conoce como el ^número $C$ ^th Franel (secuencia A000172 en la OEIS )	Pettersen	sí
4 × 4 C	4 × C	${\ Displaystyle b_ {4, C} = (4C)! (C!) ^ {12} \ sum _ {a, b, c} {\ left ({\ frac {C! ^ {2}} {a! b! c!}} \ cdot \ sum _ {k_ {12}, k_ {13}, k_ {14}, \ encima de k_ {23}, k_ {24}, k_ {34}} {{a \ elija k_ {12}} {b \ elija k_ {13}} {c \ elija k_ {14}} {c \ elija k_ {23}} {b \ elija k_ {24}} {a \ elija k_ {34}}} \ right) ^ {2}}}$ dónde: el sumando exterior se toma sobre todo una , b , c de tal manera que 0≤ un , b , c y un + b + c = 2 C . el sumando interno se toma sobre todo k ₁₂ , k ₁₃ , k ₁₄ , k ₂₃ , k ₂₄ , k ₃₄ ≥ 0 tal que k ₁₂ , k ₃₄ ≤ a y k ₁₃ , k ₂₄ ≤ b y k ₁₄ , k ₂₃ ≤ c y k ₁₂ + k ₁₃ + k ₁₄ = a - k ₁₂ + k ₂₃ + k ₂₄ = segundo - k ₁₃ + c - k ₂₃ + k ₃₄ = do - k ₁₄ + segundo - k ₂₄ + a - k ₃₄ = C La suma externa corresponde a una división de la banda en dos "subbandas" de 2 casillas cada una; los números de una , b y c de describir la división y ser del mismo para ambas sub-bandas, por lo que el sumandos puede ser cuadrado. Las variables de división se describen como: " a es el número de símbolos en la fila 1 y 2 en los primeros cuadros (es decir, símbolos que están en la fila 1 en el cuadro 1 y la fila 2 en el cuadro 2 O en la fila 1 en el cuadro 2 y la fila 2 en el cuadro 1). Entonces también será el número de símbolos en las filas 3 y 4 en los dos primeros cuadros, así como el número de símbolos en las filas 1 y 2 en los dos últimos cuadros, y el número de símbolos en las filas 3 y 4 en las dos primeras casillas. b es el número de símbolos en las filas 1 y 3 en las dos primeras casillas, junto con otras combinaciones como para la variable a . c es la cantidad de símbolos en las filas 1 y 4 en las dos primeras casillas ". Los recuentos de suma interiores el número de subbandas para un determinado una , b , c especificación: "Entre los unos símbolos que se encuentran en la fila 1 y 2 en la caja 1 y 2, k ₁₂ recuentos de cómo muchos de los que se encuentran en la fila 1 en la casilla 1 (y por lo tanto también en la fila 2 en el cuadro 2). En general, para i < j , entre los símbolos de la fila i y j en los dos primeros cuadros, k _ij indica cuántos de ellos están en la fila i en el cuadro 1 y la fila j en el recuadro 2. "	Pettersen	sí

A continuación se enumeran varios recuentos de bandas conocidos. El algoritmo de Petersen, implementado y mejorado por Silver, divide la banda en subbandas, que luego se agrupan en clases de equivalencia; es actualmente la técnica más rápida conocida para la evaluación exacta de estos b _{R, C} .

Dimensiones		Numero de bandas	Atribución	Verificado?
Banda	Bloques	Numero de bandas	Atribución	Verificado?
3 × 6	3 × 2	6! × 2! ⁶ × 10 = 460800.	Pettersen (fórmula)
3 × 9	3 × 3	9! × 3! ⁶ × 56 = 9! × 2612736 = 948109639680 ≈9.4811 × 10 ¹¹ (44 clases de equivalencia)	Varios
3 × 12	3 × 4	12! × 4! ⁶ × 346 = 31672366418991513600 ≈3.1672 × 10 ¹⁹	Stertenbrink	sí
3 × 15	3 × 5	¡15! × 5! ⁶ × 2252 ≈8.7934 × 10 ²⁷	Pettersen (fórmula)
(Los valores más grandes de 3 × C se pueden calcular fácilmente usando la fórmula dada arriba)
4 × 8	4 × 2	8! × 2! ¹² × 5016 = 828396011520 ≈8.2840 × 10 ¹¹
4 × 12	4 × 3	12! × 3! ¹² × 2180544 = 2273614462643364849254400 ≈2.2736 × 10 ²⁴	Pettersen	sí
4 × 16	4 × 4	¡dieciséis! × 4! ¹² × 1273431960 ≈9.7304 × 10 ³⁸	Plata	sí
4 × 20	4 × 5	20! × 5! ¹² × 879491145024 ≈1.9078 × 10 ⁵⁵	Russell	sí
4 × 24	4 × 6	24! × 6! ¹² × 677542845061056 ≈8.1589 × 10 ⁷²	Russell	sí
4 × 28	4 × 7	28! × 7! ¹² × 563690747238465024 ≈4.6169 × 10 ⁹¹	Russell	sí
(Silver ha realizado cálculos de hasta 4 × 100, pero no se enumeran aquí)
5 × 10	5 × 2	10! × 2! ²⁰ × 364867776 ≈1.3883 × 10 ²¹ (355 clases de equivalencia)		No
5 × 15	5 × 3	¡15! × 3! ²⁰ × 324408987992064 ≈1,5510 × 10 ⁴²	Plata	Sí ^{mismo autor, método diferente}
5 × 20	5 × 4	20! × 4! ²⁰ × 518910423730214314176 ≈5.0751 × 10 ⁶⁶	Plata	Sí ^{mismo autor, método diferente}
5 × 25	5 × 5	25! × 5! ²⁰ × 1165037550432885119709241344 ≈6,9280 × 10 ⁹³	Pettersen / Plata	No
5 × 30	5 × 6	30! × 6! ²⁰ × 3261734691836217181002772823310336 ≈1.2127 × 10 ¹²³	Pettersen / Plata	No
5 × 35	5 × 7	35! × 7! ²⁰ × 10664509989209199533282539525535793414144 ≈1,2325 × 10 ¹⁵⁴	Pettersen / Plata	No
5 × 40	5 × 8	40! × 8! ²⁰ × 39119312409010825966116046645368393936122855616 ≈4.1157 × 10 ¹⁸⁶	Pettersen / Plata	No
5 × 45	5 × 9	45! × 9! ²⁰ × 156805448016006165940259131378329076911634037242834944 ≈2,9406 × 10 ²²⁰	Pettersen / Plata	No
5 × 50	5 × 10	50! × 10! ²⁰ × 674431748701227492664421138490224315931126734765581948747776 ≈3,2157 × 10 ²⁵⁵	Pettersen / Plata	No

6 × 12	6 × 2	12! × 2! ³⁰ × 9480675056071680 = 4876139207527966044188061990912000 ≈4.8761 × 10 ³³	Pettersen	No

Rompecabezas

Número mínimo de datos

Los sudokus ordinarios ( acertijos adecuados ) tienen una solución única. Un Sudoku mínimo es un Sudoku del que no se puede quitar ninguna pista, lo que lo convierte en un Sudoku adecuado. Diferentes Sudokus mínimos pueden tener un número diferente de pistas. En esta sección se analiza el número mínimo de datos para los acertijos adecuados.

Sudoku ordinario

Un Sudoku con 17 pistas.

Un Sudoku con 17 pistas y simetría diagonal.

Un Sudoku con 18 pistas y simetría ortogonal.

Un Sudoku automórfico con 24 pistas y simetría geométrica completa.

Un Sudoku con 19 pistas y simetría ortogonal bidireccional.

Se han encontrado muchos Sudokus con 17 pistas, aunque encontrarlos no es una tarea trivial. Un artículo de Gary McGuire, Bastian Tugemann y Gilles Civario, publicado el 1 de enero de 2012, explica cómo se demostró mediante una búsqueda exhaustiva por computadora que el número mínimo de pistas en cualquier Sudoku adecuado es 17, y esto se confirmó de forma independiente en septiembre de 2013. Ed Russell proporcionó algunos rompecabezas de 17 pistas con simetría diagonal, después de una búsqueda a través de transformaciones de equivalencia de la base de datos de Gordon Royle de rompecabezas de 17 pistas. Se han encontrado sudoku con 18 pistas con simetría rotacional de 180 °, y otros con simetría ortogonal, aunque no se sabe si este número de pistas es mínimo en ambos casos. Se han encontrado rompecabezas de Sudoku con 19 pistas con simetría ortogonal bidireccional, y nuevamente se desconoce si este número de pistas es mínimo para este caso.

Se sabe que existe un Sudoku con 24 pistas, simetría diedro (simetría en ambos ejes ortogonales, simetría rotacional de 90 °, simetría rotacional de 180 ° y simetría diagonal), y también es automórfica . Nuevamente aquí, no se sabe si este número de pistas es mínimo para esta clase de Sudoku. Se cree que la menor cantidad de pistas en un Sudoku con simetría diagonal bidireccional es 18, y en al menos un caso, dicho Sudoku también exhibe automorfismo .

Entre las 5.472.730.538 cuadrículas de soluciones esencialmente diferentes , solo 4 no tienen un rompecabezas de 20 pistas; esas 4 cuadrículas tienen un rompecabezas de 21 pistas.

Sudokus de otros tamaños

Sudoku 4 × 4 (2 × 2): La menor cantidad de pistas en cualquier Sudoku 4 × 4 es 4, de los cuales hay 13 rompecabezas no equivalentes. (El número total de Sudokus mínimos no equivalentes de este tamaño es 36).
Sudoku 6 × 6 (2 × 3): La menor cantidad de pistas es 8.
Sudoku 8 × 8 (2 × 4): La menor cantidad de pistas es 14.
Sudoku 10 × 10 (2 × 5): Se ha creado al menos un rompecabezas con 22 pistas. No se sabe si es la menor cantidad posible.
Sudoku 12 × 12 (2 × 6): Se ha creado al menos un rompecabezas con 32 pistas. No se sabe si es la menor cantidad posible.
Sudoku 12 × 12 (3 × 4): Se ha creado al menos un rompecabezas con 30 pistas. No se sabe si es la menor cantidad posible.
Sudoku 15 × 15 (3 × 5): Se ha creado al menos un rompecabezas con 48 pistas. No se sabe si es la menor cantidad posible.
Sudoku 16 × 16 (4 × 4): Se ha creado al menos un rompecabezas con 55 pistas. No se sabe si es la menor cantidad posible.
Sudoku 25 × 25 (5 × 5): Se ha creado un rompecabezas con 151 pistas. No se sabe si es la menor cantidad posible.

Sudoku con restricciones adicionales

Grupos disjuntos: 11 pistas

Las restricciones adicionales (aquí, en Sudokus 3 × 3) conducen a un número mínimo de pistas menor.

Grupos disjuntos: Glenn Fowler ha demostrado algunos acertijos de 12 pistas. Más tarde, también se encontraron acertijos de 11 pistas. No se sabe si esto es lo mejor posible.
Hypercube: Guenter Stertenbrink ha demostrado varios acertijos de 8 pistas. Esto es lo mejor posible.
Sudoku mágico: Guenter Stertenbrink ha proporcionado un ejemplo de 7 pistas. No se sabe si esto es lo mejor posible.
Sudoku Anti-Knight: un ejemplo de 8 pistas ha sido proporcionado por el usuario de Reddit u / _ryokousha. Esto es lo mejor posible.
Sudoku X: Ruud van der Werf ha recopilado una lista de 7193 acertijos de 12 pistas. No se sabe si esto es lo mejor posible.
Sudoku NRC: Andries Brouwer ha proporcionado un ejemplo de 11 pistas. No se sabe si esto es lo mejor posible.
2-Sudoku cuasi-mágico: Tony Forbes ha proporcionado un ejemplo de 4 pistas. Se sospecha que esto es lo mejor posible.

Sudoku con regiones irregulares

Los rompecabezas "Du-sum-oh" (también conocido como "lugar del número de geometría") reemplazan las regiones 3 × 3 (o R × C ) del Sudoku con formas irregulares de un tamaño fijo. Bob Harris ha demostrado que siempre es posible crear ( N - 1) -clue du-sum-ohs en una cuadrícula N × N , y ha construido varios ejemplos. Johan de Ruiter ha demostrado que para cualquier N > 3 existen embaldosados polyomino que no se pueden convertir en un rompecabezas Sudoku con N formas irregulares de tamaño N .

Lugar del número de suma ("Sudoku asesino")

En el lugar de la suma numérica (Samunampure), se aplican las limitaciones habituales de no repetir el valor en ninguna fila, columna o región; Además, existen regiones adicionales ("jaulas") de varios tamaños y formas que no pueden contener repeticiones, con pistas que proporcionan la suma de dígitos dentro de la jaula (por ejemplo, una jaula de 4 celdas con suma 10 debe constar de valores 1,2,3 , 4 en algún orden). La cobertura de celda mínima conocida es de 18 celdas proporcionadas por Philip Newman, y se conjetura que es la menor cantidad posible (un ejemplo de 17 celdas implicaría un sudoku clásico de 17 pistas actualmente desconocido). El número mínimo de jaulas conocido es 7, también proporcionado por Philip Newman; no se sabe si es la menor cantidad posible.

Una variante en el sitio web de Miyuki Misawa reemplaza sumas con relaciones: las pistas son símbolos = , < y > que muestran los valores relativos de (algunas pero no todas) sumas de regiones adyacentes. Ella demuestra un ejemplo con solo ocho relaciones. No se sabe si esto es lo mejor posible.

Número máximo de datos

Un Sudoku mínimo con 40 pistas.

Se cree que la mayor cantidad de pistas para un Sudoku mínimo son 40, de las cuales solo se conocen dos. Si se elimina alguna pista de cualquiera de estos Sudokus, el rompecabezas tendría más de una solución (y por lo tanto no sería un Sudoku adecuado). En el trabajo para encontrar estos Sudokus, se catalogaron otros acertijos de alta pista, incluidos más de 6.500.000.000 de rompecabezas mínimos con 36 pistas. También se encontraron alrededor de 2600 Sudokus mínimos con 39 pistas.

Si se elimina el requisito de la unicidad de la solución, se sabe que existen pseudo-acertijos mínimos de 41 pistas, pero se pueden completar en más de una cuadrícula de soluciones. La eliminación de cualquier pista aumenta el número de finalizaciones y, desde esta perspectiva, ninguna de las 41 pistas es redundante. Con un poco más de la mitad de la cuadrícula llena de datos (41 de 81 celdas), la unicidad de la restricción de la solución aún domina sobre la restricción de mínima .

En cuanto a la mayor cantidad de pistas posibles en un Sudoku, si bien aún no representa una solución única, es cuatro menos que una cuadrícula completa (77). Si faltan dos instancias de dos números cada una y las celdas que deben ocupar son las esquinas de un rectángulo ortogonal, y exactamente dos de estas celdas están dentro de una región, hay dos formas en que se pueden sumar los últimos dígitos (dos soluciones).

Número de rompecabezas mínimos

No se conoce con precisión el número de Sudokus mínimos (Sudokus en los que no se puede eliminar ninguna pista sin perder la unicidad de la solución). Sin embargo, las técnicas estadísticas combinadas con un generador ( 'Estadísticas no sesgadas de un CSP - Un generador de sesgo controlado' ), muestran que hay aproximadamente (con un error relativo del 0.065%):

3.10 × 10 ³⁷ rompecabezas mínimos,
2.55 × 10 ²⁵ rompecabezas mínimos no esencialmente equivalentes.

Otros autores utilizaron métodos más rápidos y calcularon estadísticas de distribución precisas adicionales.

Restricciones de la geometría de la pista

Una variedad de posiciones de pistas insuficientes para un Sudoku adecuado.

Sudoku con un rectángulo vacío de 30 celdas (5 x 6). (22 pistas)

Sudoku con nueve grupos vacíos. (22 pistas)

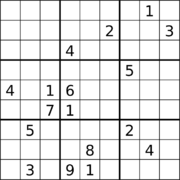
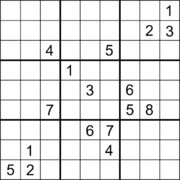
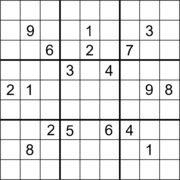
Se ha conjeturado que ningún Sudoku adecuado puede tener pistas limitadas al rango de posiciones en el espacio libre de la primera imagen de arriba. Se cree que el "agujero" ortogonal rectangular más grande (región sin pistas) en un Sudoku adecuado es un rectángulo de 30 celdas (un área rectangular de 5 × 6). Un ejemplo es un Sudoku con 22 pistas (segunda imagen). Se cree que el mayor número total de grupos vacíos (filas, columnas y cuadros) en un Sudoku es nueve. Un ejemplo es un Sudoku con 3 filas vacías, 3 columnas vacías y 3 casillas vacías (tercera imagen).

Sudokus automórficos

Una cuadrícula de Sudoku es automórfica si se puede transformar de una manera que conduzca a la cuadrícula original, cuando esa misma transformación no conduciría de otra manera a la cuadrícula original. Un ejemplo de una cuadrícula que es automórfica sería una cuadrícula que se puede rotar 180 grados dando como resultado una nueva cuadrícula donde los nuevos valores de celda son una permutación de la cuadrícula original. Los Sudokus automórficos son acertijos de Sudoku que se resuelven en una cuadrícula automórfica. A continuación se muestran dos ejemplos de Sudokus automórficos y una cuadrícula automórfica.

Un sudoku automórfico con 18 pistas (simetría diagonal bidireccional)

Un sudoku automórfico con 24 pistas (simetría diagonal bidireccional y simetría traslacional)

La cuadrícula de soluciones "más canónica" (648 automorfismos)

Número de cuadrículas esencialmente diferentes en cada
recuento de automorfismo
automatiza morfismos	No rejillas	automatiza morfismos	No rejillas
1	5472170387	18	85
2	548449	27	2
3	7336	36	15
4	2826	54	11
6	1257	72	2
8	29	108	3
9	42	162	1
12	92	648	1

En los dos primeros ejemplos, observe que si el Sudoku se gira 180 grados y las pistas se vuelven a etiquetar con la permutación (123456789) -> (987654321), vuelve al mismo Sudoku. Expresado de otra manera, estos Sudokus tienen la propiedad de que cada par de pistas rotacionales de 180 grados (a, b) sigue la regla (a) + (b) = 10.

Dado que estos Sudokus son automórficos, sus cuadrículas de soluciones también son automórficas. Además, cada celda que se resuelve tiene un socio simétrico que se resuelve con la misma técnica (y el par tomaría la forma a + b = 10). Observe que en el segundo ejemplo, el Sudoku también exhibe simetría de traslación (o repetición); las pistas se agrupan en grupos, con las pistas en cada grupo ordenadas secuencialmente (es decir, n, n + 1, n + 2 y n + 3).

La tercera imagen es la cuadrícula de solución más canónica . Esta cuadrícula tiene 648 automorfismos y contribuye a todos ~6.67 × 10 ²¹ cuadrículas de solución por un factor de 1/648 en comparación con cualquier cuadrícula no automórfica.

En estos ejemplos, los automorfismos son fáciles de identificar, pero en general el automorfismo no siempre es obvio. La tabla de la derecha muestra el número de cuadrículas de solución de Sudoku esencialmente diferentes para todos los automorfismos existentes.

Detalles de enumerar cuadrículas distintas (9 × 9)

Se desarrolló una técnica de enumeración basada en la generación de bandas que es significativamente menos intensiva desde el punto de vista informático. La estrategia comienza analizando las permutaciones de la banda superior utilizadas en soluciones válidas. Una vez que se identifican las simetrías Band1 y la clase de equivalencia para las soluciones parciales, se construyen las terminaciones de las dos bandas inferiores y se cuentan para cada clase de equivalencia.

Contando las permutaciones de la banda superior

1	2	3
4	5	6
7	8	9

El algoritmo Band1 procede de la siguiente manera:

Elija un etiquetado canónico de los dígitos asignando valores para B1 (consulte la cuadrícula) y calcule el resto de las permutaciones de Band1 relativas a B1.
Calcule las permutaciones de B2 dividiendo los valores de la celda B1 entre los tripletes de la fila B2 . A partir de las combinaciones de tripletes, calcule las permutaciones B2. Hay k = 0..3 formas de elegir:

Valores de B1 r11 para B2 r22, el resto debe ir a r16,

Valores de B1 r12 para B2 r23, el resto debe ir a r16,

Valores de B1 r13 para B2 r21, el resto debe ir a r16, es decir

{\ displaystyle {\ mbox {N combinaciones para B2}} = \ sum _ {k = 0} ^ {3} {{3 \ choose k} ^ {3}}}

(Esta expresión puede generalizarse a cualquier variante de banda de caja R × 3. (Pettersen). Por lo tanto, B2 aporta 56 × 6 ³ permutaciones.

Las opciones para los tripletes B3 están determinadas por filas por los tripletes de las filas B1 B2. B3 siempre aporta 6 ³ permutaciones.

¡Las permutaciones para Band1 son $9! \times 56 \times 6 6 = 9! \times 2612736 \approx 9,48 \times 1011$ .

Detalles de permutación Band1

Etiquetas de triplete rBR (caja / fila)

r	1	1
r	1	2
r	1	3

r	2	1
r	2	2
r	2	3

r	3	1
r	3	2
r	3	3

Las permutaciones de B1 son el número de formas de volver a etiquetar los 9 dígitos, ¡9! = 362880. Contar las permutaciones de B2 es más complicado, porque las opciones de B2 dependen de los valores de B1. (Esta es una representación visual de la expresión dada anteriormente). El cálculo condicional necesita una rama (subcálculo) para cada alternativa. Afortunadamente, solo hay 4 casos para el triplete B2 superior (r21): contiene 0, 1, 2 o 3 de los dígitos del triplete de la fila central B1 (r12). Una vez que se hace esta elección de la fila superior de B2, el resto de las combinaciones de B2 se arreglan. Las etiquetas del triplete de la fila Band1 se muestran a la derecha.

(Nota: las combinaciones condicionales se vuelven cada vez más difíciles a medida que el cálculo avanza a través de la cuadrícula. En este punto, el impacto es mínimo).

Caso 0 Trillizos de células coincidentes

1	2	3
4	5	6
7	8	9

7	8	9
1	2	3
4	5	6

4	5	6
7	8	9
1	2	3

Caso 0: Sin superposición. Las opciones para los trillizos se pueden determinar por eliminación.

r21 no puede ser r11 o r12, por lo que debe ser = r13; r31 debe ser = r12 etc.

El diagrama del Caso 0 muestra esta configuración, donde las celdas rosadas son valores de triplete que se pueden organizar en cualquier orden dentro del triplete. ¡Cada triplete tiene 3! = 6 permutaciones. Los 6 tripletes aportan 6 ⁶ permutaciones.

Caso 3: Coincidencia de 3 dígitos: triplete r21 = r12. Se aplica la misma lógica que en el caso 0, pero con un uso de triplete diferente. El triplete r22 debe ser = r13, etc. El número de permutaciones es nuevamente 6 ⁶ (Felgenhauer / Jarvis). Llame a los casos 0 y 3 el caso de coincidencia pura .

Coincidencia del caso 1: opciones de celdas de triplete

1	2	3
4	5	6
7	8	9

3	3	2
1	3	2
1	2	1

3	2	1
3	2	1
3	2	1

Caso 1: 1 coincidencia para r21 de r12

En el diagrama del Caso 1, las celdas B1 muestran valores canónicos, que están codificados por colores para mostrar su distribución por filas en tripletes B2. Los colores reflejan la distribución, pero no la ubicación ni los valores. Para este caso: el triplete de la fila superior B2 (r21) tiene 1 valor del triplete del medio B1, ahora se pueden deducir los otros colorantes. Por ejemplo, la coloración del triplete de la fila inferior B2 (r23) es forzada por r21: los otros 2 valores intermedios de B1 deben ir a la parte inferior, etc. Complete el número de opciones B2 para cada color, 3..1, comenzando en la parte superior izquierda. La codificación de colores B3 se omite ya que las opciones B3 están determinadas por filas por B1, B2. ¡B3 siempre aporta 3! permutaciones por triplete de fila, o 6 ³ para el bloque.

Para B2, los valores de triplete pueden aparecer en cualquier posición, ¡así que un 3! todavía se aplica el factor de permutación, para cada triplete. Sin embargo, dado que algunos de los valores se emparejaron en relación con su origen, el uso de los recuentos de opciones sin procesar sobrecontaría el número de permutaciones, debido a la intercambiabilidad dentro del emparejamiento. Los recuentos de opciones deben dividirse por el tamaño permutado de su agrupación (2), ¡aquí 2! = 2 (Ver ) El par en cada fila cancela los 2 para los recuentos de la opción B2, dejando una contribución de B2 de $3$ $3$ $\times 6$ $3$ . La contribución combinada B2 × B3 es $3$ $3$ $\times 6$ $6$ . ${\ Displaystyle \ color {Blue} {n \ Choose k}}$

Coincidencia del caso 2: opciones de celdas de triplete

1	2	3
4	5	6
7	8	9

3	2	3
2	1	3
2	1	1

3	2	1
3	2	1
3	2	1

Caso 2: 2 coincidencias para r21 desde r12. Se aplica la misma lógica que en el caso 1, pero con las agrupaciones de columnas de recuento de la opción B2 invertidas. El caso 3 también aporta 3 ³ × 6 ⁶ permutaciones.

¡Sumando los 4 casos para Band1 B1..B3 da $9! \times 2 \times (3 3 + 1) \times 6 6 = 9! 56 \times 6 6$ permutaciones.

Simetrías Band1 y clases de equivalencia

Las simetrías se utilizan para reducir el esfuerzo computacional para enumerar las permutaciones de Band1. Una simetría es una operación que conserva la calidad de un objeto. Para una cuadrícula de Sudoku, una simetría es una transformación cuyo resultado también es una cuadrícula válida. Las siguientes simetrías se aplican de forma independiente para la banda superior:

Los valores del bloque B1 se pueden volver a etiquetar, dando 9! permutaciones
Los bloques B1..3 pueden intercambiarse, con 3! = 6 permutaciones
Las filas 1..3 pueden intercambiarse, con 3! = 6 permutaciones
Dentro de cada bloque, las 3 columnas se pueden intercambiar, dando 3! ³ = 6 ³ permutaciones.

¡Combinadas, las simetrías dan 9! × 6 ⁵ = 362880 × 7776 permutaciones equivalentes para cada solución de Band1.

Una simetría define una relación de equivalencia , aquí, entre las soluciones, y divide las soluciones en un conjunto de clases de equivalencia . Las simetrías de fila, columna y bloque de Band1 dividen las permutaciones en (no menos de) 336 (56 × 6) clases de equivalencia con (hasta) 6 ⁵ permutaciones en cada una, y 9! permutaciones de reetiquetado para cada clase. (Se aplican advertencias mínimas / máximas ya que es posible que algunas permutaciones no produzcan elementos distintos debido al reetiquetado). ${\ Displaystyle 56 \ times 6 ^ {6}}$

Dado que la solución para cualquier miembro de una clase de equivalencia se puede generar a partir de la solución de cualquier otro miembro, solo necesitamos enumerar las soluciones para un solo miembro para enumerar todas las soluciones de todas las clases. Dejar

sb: ser una permutación válida de la banda superior
Sb = [sb]: ser una clase de equivalencia, relativa a sb y alguna relación de equivalencia
Sb.z = | Sb | : el tamaño de Sb, sea el número de elementos sb (permutaciones) en [sb]
Sb.n: sea el número de completaciones de Band2,3 para (cualquier) sb en Sb
{Sb}: sea el conjunto de todas las clases de equivalencia de Sb en relación con la relación de equivalencia
{Sb} .z = | {Sb} | : sea el número de clases de equivalencia

El número total de soluciones N es entonces:

N =Sb.z × Sb.n

Solución y conteo de simetría de permutación.

Las simetrías Band1 (arriba) son simetrías de permutación de soluciones definidas de modo que una solución permutada también sea una solución. Con el fin de enumerar soluciones, se puede usar una simetría de conteo para completar la cuadrícula para definir clases de equivalencia de banda que produzcan un número mínimo de clases.

El recuento de simetría divide las permutaciones Band1 válidas en clases que imponen las mismas restricciones de finalización en las bandas inferiores; todos los miembros de una clase de equivalencia de simetría de recuento de bandas deben tener el mismo número de terminaciones de cuadrícula, ya que las restricciones de terminación son equivalentes. Las restricciones de simetría de recuento se identifican mediante los tripletes de la columna Band1 (un conjunto de valores de columna, sin orden de elementos implícito). Utilizando la simetría de conteo de bandas, se estableció un conjunto generador mínimo de 44 clases de equivalencia.

(1) Ejemplo de Band1

1	2	3
4	5	6
7	8	9

5	8	6
9	1	7
4	3	2

7	4	9
8	2	3
5	1	6

(2) Tríos de columnas

1	2	3
4	5	6
7	8	9

4	1	2
5	3	6
9	8	7

5	1	3
7	2	6
8	4	9

(3) Trillizos de Col ordenados

1	2	3
4	5	6
7	8	9

1	3	5
2	6	7
4	9	8

1	2	4
3	6	5
8	7	9

La siguiente secuencia demuestra el mapeo de una configuración de banda a una clase de equivalencia de simetría de conteo. Comience con una configuración de banda válida (1). Construya tripletes de columnas ordenando los valores de las columnas dentro de cada columna. Esta no es una banda de Sudoku válida, pero impone las mismas restricciones en las bandas inferiores que en el ejemplo (2). Construya un ID de clase de equivalencia a partir de los valores del triplete de columnas B2, B3. Utilice intercambios de columnas y recuadros para lograr la identificación lexicográfica más baja. La última figura muestra el orden de columnas y recuadros para el ID: 124 369 578 138 267 459. Todas las permutaciones Band1 con este ID de simetría de conteo tendrán el mismo número de terminaciones de cuadrícula que el ejemplo original. Se puede utilizar una extensión de este proceso para construir las clases de equivalencia de simetría de conteo de bandas más grandes posibles (3).

Tenga en cuenta que, si bien los tripletes de columna se utilizan para construir e identificar las clases de equivalencia, los miembros de la clase en sí son las permutaciones Band1 válidas: el tamaño de la clase (Sb.z) refleja las permutaciones de tripletes de columna compatibles con los requisitos de solución de una regla . La simetría de conteo es una propiedad de finalización y se aplica solo a una cuadrícula parcial (banda o pila). La simetría de la solución para preservar las soluciones se puede aplicar a cuadrículas parciales (bandas, pilas) o soluciones de cuadrícula completa. Por último, tenga en cuenta que la simetría de conteo es más restrictiva que la simple igualdad de conteo de finalización numérica: dos bandas (distintas) pertenecen a la misma clase de equivalencia de simetría de conteo solo si imponen restricciones de finalización equivalentes.

Detalles de la reducción de la banda 1

Las simetrías agrupan objetos similares en clases de equivalencia . Es necesario distinguir dos números para las clases de equivalencia y las simetrías de banda como se usa aquí, un tercero:

el número de clases de equivalencia ({Sb} .n).
la cardinalidad , tamaño o número de elementos en una clase de equivalencia, que puede variar según la clase (Sb.z)
el número de finalizaciones de Band2,3 compatibles con un miembro de una clase de equivalencia de Band1 (Sb.n)

Las simetrías Band1 (6 ⁵ ) dividen las permutaciones válidas de Band1 (56 × 6 ⁶ ) en (no menos de) 336 (56 × 6) clases de equivalencia con (hasta) permutaciones cada una. Las advertencias de no menor que y hasta máximo son necesarias, ya que algunas combinaciones de las transformaciones pueden no producir resultados distintos, cuando se requiere el reetiquetado (ver más abajo). En consecuencia, algunas clases de equivalencia pueden contener menos de 6 ⁵ permutaciones distintas y es posible que no se alcance el número mínimo teórico de clases. ${\ Displaystyle 6 ^ {5}}$

Cada una de las permutaciones Band1 válidas se puede expandir (completar) en un número específico de soluciones con las permutaciones Band2,3. En virtud de su similitud, cada miembro de una clase de equivalencia tendrá el mismo número de terminaciones. En consecuencia, solo necesitamos construir las soluciones para un miembro de cada clase de equivalencia y luego multiplicar el número de soluciones por el tamaño de la clase de equivalencia. Aún nos queda la tarea de identificar y calcular el tamaño de cada clase de equivalencia. Un mayor progreso requiere la aplicación diestra de técnicas computacionales para catalogar (clasificar y contar) las permutaciones en clases de equivalencia.

Felgenhauer / Jarvis catalogaron las permutaciones de Band1 utilizando ID ordenados lexicográficos basados en los dígitos ordenados de los bloques B2,3. El bloque 1 utiliza una asignación de dígitos canónicos y no es necesario para una identificación única. La identificación y vinculación de la clase de equivalencia utiliza la identificación más baja dentro de la clase.

La aplicación de las permutaciones de simetría (2 × 6 ² ) B2,3 produce 36288 (28 × 6 ⁴ ) clases de equivalencia, cada una de tamaño 72. Dado que el tamaño es fijo, el cálculo solo necesita encontrar los 36288 ID de clase de equivalencia. (Nota: en este caso, para cualquier permutación de Band1, la aplicación de estas permutaciones para lograr la ID más baja proporciona un índice a la clase de equivalencia asociada).

La aplicación del resto de las simetrías de bloque, columna y fila proporcionó una mayor reducción, es decir, la asignación de los 36288 ID en menos clases de equivalencia más grandes. Cuando el etiquetado canónico de B1 se pierde a través de una transformación, el resultado se vuelve a etiquetar al uso canónico de B1 y luego se cataloga con este ID. Este enfoque generó 416 clases de equivalencia, algo menos efectivo que el límite mínimo teórico de 336 para una reducción total. La aplicación de patrones de simetría de conteo para pares de dígitos duplicados logró una reducción a 174 y luego a 71 clases de equivalencia. La introducción de clases de equivalencia basadas en la simetría de conteo de bandas (posterior a Felgenhauer / Jarvis de Russell) redujo las clases de equivalencia a un conjunto generador mínimo de 44.

La diversidad de la ~2.6 × 10 ⁶ , 56 × 6 ⁶ Las permutaciones de Band1 se pueden reducir a un conjunto de 44 clases de equivalencia de Band1. Cada una de las 44 clases de equivalencia se puede expandir a millones de soluciones completas distintas, pero todo el espacio de la solución tiene un origen común en estas 44. Las 44 clases de equivalencia también juegan un papel central en otros enfoques de enumeración, y la especulación volverá a la características de las 44 clases cuando se exploren más adelante las propiedades del rompecabezas.

Finalización y resultados de la banda 2-3

La enumeración de las soluciones de Sudoku se divide en una etapa de configuración inicial y luego en dos bucles anidados. Inicialmente, todas las permutaciones válidas de Band1 se agrupan en clases de equivalencia, cada una de las cuales impone una restricción común en las terminaciones de Band2,3. Para cada una de las clases de equivalencia de Band1, se deben enumerar todas las posibles soluciones de Band2,3. Un bucle Band1 externo itera sobre las 44 clases de equivalencia. En el bucle interno, se encuentran y se cuentan todas las terminaciones de banda inferior para cada una de las clases de equivalencia de Band1.

El cálculo necesario para la búsqueda de la solución de banda inferior se puede minimizar mediante el mismo tipo de aplicación de simetría que se utiliza para Band1. ¡Hay 6! (720) permutaciones para los 6 valores en la columna 1 de Band2,3. La aplicación de las permutaciones de la banda inferior (2) y la fila dentro de la banda (6 × 6) crea 10 clases de equivalencia de tamaño 72. En este punto, al completar 10 conjuntos de soluciones para las 48 celdas restantes con un descenso recursivo, el algoritmo de retroceso es factible con 2 PC de clase GHz, por lo que no se requiere una mayor simplificación para llevar a cabo la enumeración. Con este enfoque, se ha demostrado que el número de formas de completar una cuadrícula de Sudoku en blanco es 6,670,903,752,021,072,936,960 (6,67 × 10 ²¹ ).

El resultado, como confirmó Russell, también contiene la distribución de los recuentos de soluciones para las 44 clases de equivalencia. Los valores listados son antes de la aplicación del 9! factor para el etiquetado y los dos 72 factores (72 ² = 5184) para cada una de las permutaciones Stack 2,3 y Band2,3. El número de terminaciones para cada clase es consistentemente del orden de 100.000.000, mientras que el número de permutaciones de Band1 cubiertas por cada clase varía sin embargo de 4 a 3240. Dentro de este amplio rango de tamaño, hay claramente dos grupos. Clasificadas por tamaño, las 33 clases inferiores promedian ~ 400 permutaciones / clase, mientras que las 11 superiores promedian ~ 2100. Aún no se ha examinado la disparidad en la coherencia entre las distribuciones por tamaño y número de terminaciones o la separación en dos grupos por tamaño.

Ver también

Explosión combinatoria (con resumen del recuento de cuadrículas de Sudoku en comparación con cuadrados latinos)
Enlaces de baile
Glosario de Sudoku
Sudokian
Código sudoku

Referencias

Otras lecturas

Rosenhouse, Jason ; Taalman, Laura (2011). Tomando el Sudoku en serio: las matemáticas detrás del rompecabezas de lápiz más popular del mundo . Prensa de la Universidad de Oxford.

enlaces externos

El algoritmo de mapa de diferencias de V. Elser también resuelve Sudoku
Sudoku Puzzle: un ejercicio de programación de restricciones y Visual Prolog 7 por Carsten Kehler Holst (en Visual Prolog )
Sudoku Squares and Chromatic Polynomials de Herzberg y Murty, trata los rompecabezas de Sudoku como problemas de coloración de vértices en la teoría de grafos .

Languages

In other projects

Matemáticas del Sudoku - Mathematics of Sudoku

Visión general

Contexto matemático

Sudokus de tablas de grupo

Variantes

Regiones rectangulares

Sudokus de rompecabezas

Soluciones

Sudoku ordinario

Todas las soluciones

Soluciones esencialmente diferentes

Transformaciones que preservan la validez

El grupo de simetría del sudoku

Puntos fijos y lema de Burnside

Subgrupos de estabilizadores

Número de cuadrículas esencialmente equivalentes

Otras variantes

Sudoku con restricciones adicionales

Sudoku con regiones rectangulares

Método de estimación

Numero de bandas

Rompecabezas

Número mínimo de datos

Sudoku ordinario

Sudokus de otros tamaños

Sudoku con restricciones adicionales

Sudoku con regiones irregulares

Lugar del número de suma ("Sudoku asesino")

Número máximo de datos

Número de rompecabezas mínimos

Restricciones de la geometría de la pista

Sudokus automórficos

Detalles de enumerar cuadrículas distintas (9 × 9)

Contando las permutaciones de la banda superior

Detalles de permutación Band1

Simetrías Band1 y clases de equivalencia

Solución y conteo de simetría de permutación.

Detalles de la reducción de la banda 1

Finalización y resultados de la banda 2-3

Ver también

Referencias

Otras lecturas

enlaces externos