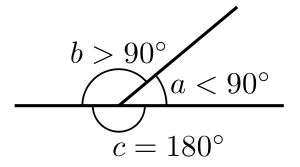Ángulo - Angle
En la geometría euclidiana , un ángulo es la figura formada por dos rayos , llamados lados del ángulo, que comparten un punto final común, llamado vértice del ángulo. Los ángulos formados por dos rayos se encuentran en el plano que contiene los rayos. Los ángulos también se forman por la intersección de dos planos. Estos se llaman ángulos diedros . Dos curvas que se cruzan definen también un ángulo, que es el ángulo de las tangentes en el punto de intersección. Por ejemplo, el ángulo esférico formado por dos grandes círculos en una esfera es igual al ángulo diedro entre los planos que contienen los grandes círculos.
Ángulo también se usa para designar la medida de un ángulo o de una rotación . Esta medida es la relación entre la longitud de un arco circular y su radio . En el caso de un ángulo geométrico, el arco está centrado en el vértice y delimitado por los lados. En el caso de una rotación, el arco está centrado en el centro de la rotación y delimitado por cualquier otro punto y su imagen por la rotación.
Historia y etimología
La palabra ángulo proviene de la palabra latina angulus , que significa "esquina"; las palabras afines son el griego ἀγκύλος (ankylοs) , que significa "torcido, curvado", y la palabra inglesa " tobillo ". Ambos están conectados con el proto-indoeuropeo de la raíz * ank- , que significa "doblar" o "arco".
Euclides define un ángulo plano como la inclinación entre sí, en un plano, de dos líneas que se encuentran y no son rectas entre sí. Según Proclus , un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemus , quien consideraba un ángulo como una desviación de una línea recta ; el segundo por Carpo de Antioquía , quien lo consideró como el intervalo o espacio entre las líneas que se cruzan; Euclides adoptó el tercer concepto.
Identificando ángulos
En expresiones matemáticas , es común usar letras griegas ( α , β , γ , θ , φ ,...) Como variables que denotan el tamaño de algún ángulo (para evitar confusión con su otro significado, el símbolo π generalmente no se usa para este propósito). También se utilizan letras romanas minúsculas ( a , b , c ,...), Así como letras romanas mayúsculas en el contexto de los polígonos . Consulte las figuras de este artículo para ver ejemplos.
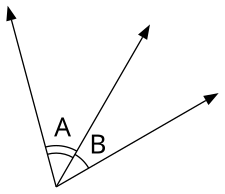
En las figuras geométricas, los ángulos también pueden identificarse mediante las etiquetas adheridas a los tres puntos que los definen. Por ejemplo, el ángulo en el vértice A encerrado por los rayos AB y AC (es decir, las líneas del punto A al punto B y del punto A al punto C) se denota ∠BAC (en Unicode U + 2220 ∠ ANGLE ) o . Cuando no exista riesgo de confusión, el ángulo a veces puede denominarse simplemente por su vértice (en este caso, "ángulo A").
Potencialmente, un ángulo denotado como, digamos, ∠BAC, podría referirse a cualquiera de los cuatro ángulos: el ángulo en sentido horario de B a C, el ángulo en sentido antihorario de B a C, el ángulo en sentido horario de C a B, o el ángulo en sentido antihorario de C a B, donde la dirección en la que se mide el ángulo determina su signo (consulte Ángulos positivos y negativos ). Sin embargo, en muchas situaciones geométricas, es obvio por el contexto que se refiere al ángulo positivo menor o igual a 180 grados, en cuyo caso no surge ninguna ambigüedad. De lo contrario, se puede adoptar una convención para que ∠BAC siempre se refiera al ángulo en sentido antihorario (positivo) de B a C, y ∠CAB al ángulo en sentido contrario a las agujas del reloj (positivo) de C a B.
Tipos de ángulos
Ángulos individuales
Existe una terminología común para los ángulos, cuya medida siempre es no negativa (ver § Ángulos positivos y negativos ):
- Un ángulo igual a 0 ° o no girado se llama ángulo cero.
- Un ángulo más pequeño que un ángulo recto (menos de 90 °) se llama ángulo agudo ("agudo" significa " agudo ").
- Un ángulo igual a 1/4 girar (90 ° o π/2radianes) se llama ángulo recto . Se dice que dos líneas que forman un ángulo recto son normales , ortogonales o perpendiculares .
- Un ángulo más grande que un ángulo recto y más pequeño que un ángulo recto (entre 90 ° y 180 °) se llama ángulo obtuso ("obtuso" significa "romo").
- Un ángulo igual a 1/2 giro (180 ° o π radianes) se llama ángulo recto .
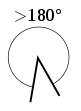
- Un ángulo mayor que un ángulo recto pero menos de 1 vuelta (entre 180 ° y 360 °) se denomina ángulo reflejo .
- Un ángulo igual a 1 vuelta (360 ° o 2 pi radianes) se llama un ángulo completo , ángulo completo , ángulo redondo o una Perigon .
- Un ángulo que no es múltiplo de un ángulo recto se llama ángulo oblicuo .
Los nombres, intervalos y unidades de medida se muestran en la siguiente tabla:
| Nombre | cero | agudo | ángulo recto | obtuso | derecho | reflejo | perigon | |||
| Unidad | Intervalo | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| girar | 0 turno | (0, 1/4) girar | 1/4 girar | (1/4, 1/2) girar | 1/2 girar | (1/2, 1 turno | 1 turno | |||
| radián | 0 rad | (0, 1/2π ) rad | 1/2π rad | (1/2π , π ) rad | π rad | ( π , 2 π ) rad | 2 π rad | |||
| la licenciatura | 0 ° | (0, 90) ° | 90 ° | (90, 180) ° | 180 ° | (180, 360) ° | 360 ° | |||
| vamos | 0 g | (0, 100) g | 100 g | (100, 200) g | 200 g | (200, 400) g | 400 g | |||
Pares de ángulos de equivalencia
- Se dice que los ángulos que tienen la misma medida (es decir, la misma magnitud) son iguales o congruentes . Un ángulo se define por su medida y no depende de las longitudes de los lados del ángulo (por ejemplo, todos los ángulos rectos tienen la misma medida).
- Dos ángulos que comparten lados terminales, pero que difieren en tamaño por un múltiplo entero de una vuelta, se denominan ángulos coterminales .
- Un ángulo de referencia es la versión aguda de cualquier ángulo determinado restando o sumando repetidamente un ángulo recto (1/2girar, 180 °, o π radianes), según sea necesario, hasta que la magnitud del resultado sea un ángulo agudo, un valor entre 0 y1/4 girar, 90 °, o π/2radianes. Por ejemplo, un ángulo de 30 grados tiene un ángulo de referencia de 30 grados y un ángulo de 150 grados también tiene un ángulo de referencia de 30 grados (180-150). Un ángulo de 750 grados tiene un ángulo de referencia de 30 grados (750–720).
Pares de ángulos verticales y adyacentes

Cuando dos líneas rectas se cruzan en un punto, se forman cuatro ángulos. Por pares, estos ángulos se nombran de acuerdo con su ubicación entre sí.
- Un par de ángulos opuestos entre sí, formados por dos líneas rectas que se cruzan y que forman una forma similar a una "X", se denominan ángulos verticales o ángulos opuestos o ángulos verticalmente opuestos . Se abrevian como vert. opp. ∠s .
- La igualdad de ángulos verticalmente opuestos se llama teorema del ángulo vertical . Eudemo de Rodas atribuyó la prueba a Tales de Mileto . La proposición mostró que dado que ambos de un par de ángulos verticales son suplementarios a ambos ángulos adyacentes, los ángulos verticales son iguales en medida. Según una nota histórica, cuando Tales visitó Egipto, observó que cada vez que los egipcios trazaban dos líneas que se cruzaban, medían los ángulos verticales para asegurarse de que fueran iguales. Thales concluyó que se podría probar que todos los ángulos verticales son iguales si se aceptaran algunas nociones generales como:
- Todos los ángulos rectos son iguales.
- Iguales sumados a iguales son iguales.
- Los iguales restados de los iguales son iguales.
- Cuando dos ángulos adyacentes forman una línea recta, son suplementarios. Por lo tanto, si asumimos que la medida del ángulo A es igual a x , entonces la medida del ángulo C sería 180 ° - x . De manera similar, la medida del ángulo D sería 180 ° - x . Tanto el ángulo C como el ángulo D tienen medidas iguales a 180 ° - x y son congruentes. Desde ángulo B es complementario a ambos ángulos C y D , cualquiera de estas medidas de los ángulos se pueden usar para determinar la medida del ángulo B . Usando la medida del ángulo C o del ángulo D , encontramos que la medida del ángulo B es 180 ° - (180 ° - x ) = 180 ° - 180 ° + x = x . Por lo tanto, tanto el ángulo A como el ángulo B tienen medidas iguales ax y son iguales en medida.
- Ángulos adyacentes , a menudo abreviados como adj. ∠s , son ángulos que comparten un vértice y una arista comunes pero no comparten ningún punto interior. En otras palabras, son ángulos que están uno al lado del otro, o adyacentes, compartiendo un "brazo". Los ángulos adyacentes que suman un ángulo recto, un ángulo recto o un ángulo completo son especiales y se denominan respectivamente ángulos complementarios , suplementarios y explementarios (ver § Combinación de pares de ángulos a continuación).
Una transversal es una línea que cruza un par de líneas (a menudo paralelas) y está asociada con ángulos alternos internos , ángulos correspondientes , ángulos internos y ángulos externos .
Combinando pares de ángulos
Tres pares de ángulos especiales involucran la suma de ángulos:
- Los ángulos complementarios son pares de ángulos cuyas medidas suman un ángulo recto (1/4 girar, 90 °, o π/2radianes). Si los dos ángulos complementarios son adyacentes, sus lados no compartidos forman un ángulo recto. En geometría euclidiana, los dos ángulos agudos de un triángulo rectángulo son complementarios, porque la suma de los ángulos internos de un triángulo es 180 grados, y el ángulo recto en sí representa 90 grados.
- El adjetivo complementario proviene del latín complemento , asociado al verbo complere , "llenar". Un ángulo agudo se "rellena" con su complemento para formar un ángulo recto.
- La diferencia entre un ángulo y un ángulo recto se denomina complemento del ángulo.
- Si los ángulos A y B son complementarios, se mantienen las siguientes relaciones:
- (La tangente de un ángulo es igual a la cotangente de su complemento y su secante es igual a la cosecante de su complemento).
- El prefijo " co- " en los nombres de algunas proporciones trigonométricas se refiere a la palabra "complementaria".
- Dos ángulos que suman un ángulo recto (1/2giro, 180 ° o π radianes) se denominan ángulos suplementarios .
- Si los dos ángulos suplementarios son adyacentes (es decir, tienen un vértice común y comparten solo un lado), sus lados no compartidos forman una línea recta . Estos ángulos se denominan par de ángulos lineales . Sin embargo, los ángulos suplementarios no tienen que estar en la misma línea y pueden separarse en el espacio. Por ejemplo, los ángulos adyacentes de un paralelogramo son suplementarios y los ángulos opuestos de un cuadrilátero cíclico (uno cuyos vértices caen todos en un solo círculo) son suplementarios.
- Si un punto P es exterior a un círculo con centro O, y si las rectas tangentes de P tocan el círculo en los puntos T y Q, entonces ∠TPQ y ∠TOQ son suplementarios.
- Los senos de los ángulos suplementarios son iguales. Sus cosenos y tangentes (a menos que no estén definidos) son iguales en magnitud pero tienen signos opuestos.
- En geometría euclidiana, cualquier suma de dos ángulos en un triángulo es suplementaria al tercero, porque la suma de los ángulos internos de un triángulo es un ángulo recto.
- Dos ángulos que suman un ángulo completo (1 vuelta, 360 ° o 2 π radianes) se denominan ángulos explementarios o ángulos conjugados .
- La diferencia entre un ángulo y un ángulo completo se denomina el complemento del ángulo o conjugado de un ángulo.
- Un ángulo que es parte de un polígono simple se llama ángulo interior si se encuentra en el interior de ese polígono simple. Un polígono cóncavo simple tiene al menos un ángulo interior que es un ángulo reflejo.
- En geometría euclidiana , las medidas de los ángulos interiores de un triángulo suman π radianes, 180 ° o1/2girar; las medidas de los ángulos interiores de un cuadrilátero convexo simple suman 2 π radianes, 360 ° o 1 vuelta. En general, las medidas de los ángulos interiores de un polígono convexo simple con n lados suman ( n - 2) π radianes, o ( n - 2) 180 grados, ( n - 2) 2 ángulos rectos o ( n - 2)1/2 girar.
- El suplemento de un ángulo interior se denomina ángulo exterior , es decir, un ángulo interior y un ángulo exterior forman un par lineal de ángulos . Hay dos ángulos exteriores en cada vértice del polígono, cada uno determinado al extender uno de los dos lados del polígono que se encuentran en el vértice; estos dos ángulos son verticales y, por tanto, son iguales. Un ángulo exterior mide la cantidad de rotación que uno tiene que hacer en un vértice para trazar el polígono. Si el ángulo interior correspondiente es un ángulo reflejo, el ángulo exterior debe considerarse negativo . Incluso en un polígono no simple, puede ser posible definir el ángulo exterior, pero uno tendrá que elegir una orientación del plano (o superficie ) para decidir el signo de la medida del ángulo exterior.
- En geometría euclidiana, la suma de los ángulos exteriores de un polígono convexo simple, si solo se supone uno de los dos ángulos exteriores en cada vértice, será una vuelta completa (360 °). El ángulo exterior aquí podría llamarse un ángulo exterior suplementario . Los ángulos exteriores se utilizan comúnmente en los programas de Logo Turtle al dibujar polígonos regulares.
- En un triángulo , las bisectrices de dos ángulos exteriores y la bisectriz del otro ángulo interior son concurrentes (se encuentran en un solo punto).
- En un triángulo, tres puntos de intersección, cada uno de una bisectriz de ángulo externo con el lado extendido opuesto , son colineales .
- En un triángulo, tres puntos de intersección, dos de ellos entre una bisectriz de ángulo interior y el lado opuesto, y el tercero entre la otra bisectriz de ángulo exterior y el lado opuesto extendido, son colineales.
- Algunos autores usan el nombre de ángulo exterior de un polígono simple para referirse simplemente al ángulo exterior del complemento (¡ no al complemento!) Del ángulo interior. Esto entra en conflicto con el uso anterior.
- El ángulo entre dos planos (como dos caras adyacentes de un poliedro ) se llama ángulo diedro . Puede definirse como el ángulo agudo entre dos líneas normales a los planos.
- El ángulo entre un plano y una línea recta que se cruza es igual a noventa grados menos el ángulo entre la línea que se cruza y la línea que pasa por el punto de intersección y es normal al plano.
Medición de ángulos
El tamaño de un ángulo geométrico generalmente se caracteriza por la magnitud de la rotación más pequeña que asigna uno de los rayos al otro. Se dice que los ángulos que tienen el mismo tamaño son iguales o congruentes o iguales en medida .
En algunos contextos, como identificar un punto en un círculo o describir la orientación de un objeto en dos dimensiones con respecto a una orientación de referencia, los ángulos que difieren en un múltiplo exacto de una vuelta completa son efectivamente equivalentes. En otros contextos, como identificar un punto en una curva en espiral o describir la rotación acumulativa de un objeto en dos dimensiones en relación con una orientación de referencia, los ángulos que difieren en un múltiplo distinto de cero de una vuelta completa no son equivalentes.
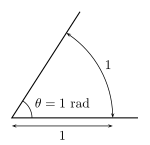
Para medir un ángulo θ , se dibuja un arco circular centrado en el vértice del ángulo, por ejemplo, con un compás . La razón de la longitud s del arco por el radio r del círculo es el número de radianes en el ángulo. Convencionalmente, en matemáticas y en el SI , el radián se trata como si fuera igual al valor adimensional 1.
El ángulo expresado en otra unidad angular se puede obtener multiplicando el ángulo por una constante de conversión adecuada de la forma k/2 π, donde k es la medida de un giro completo expresado en la unidad elegida (por ejemplo, k = 360 ° para grados o 400 grad para gradianes ):
El valor de θ así definido es independiente del tamaño del círculo: si se cambia la longitud del radio, la longitud del arco cambia en la misma proporción, por lo que la relación s / r no se modifica.
En particular, la medida del ángulo en radianes también se puede interpretar como la longitud del arco de su círculo unitario correspondiente:
Postulado de la suma de ángulos
El postulado de la suma de ángulos establece que si B está en el interior del ángulo AOC, entonces
La medida del ángulo AOC es la suma de la medida del ángulo AOB y la medida del ángulo BOC.
Unidades
A lo largo de la historia, los ángulos se han medido en muchas unidades diferentes . Estas se conocen como unidades angulares , siendo las unidades más contemporáneas el grado (°), el radianes (rad) y el gradian (grad), aunque muchas otras se han utilizado a lo largo de la historia .
Los ángulos expresados en radianes son adimensionales para el análisis dimensional .
La mayoría de las unidades de medida angular se definen de modo que un giro (es decir, un círculo completo) sea igual an unidades, para algún número entero n . Las dos excepciones son el radianes (y sus submúltiplos decimales) y la parte de diámetro.
Un radianes es el ángulo subtendido por un arco de un círculo que tiene la misma longitud que el radio del círculo. El radianes es la cantidad derivada de medición angular en el sistema SI . Por definición, no tiene dimensiones , aunque puede especificarse como rad para evitar ambigüedades. Los ángulos medidos en grados se muestran con el símbolo °. Las subdivisiones del grado son minuto (símbolo ′, 1 ′ = 1/60 °) y segundo {símbolo ″, 1 ″ = 1/3600 °}. Un ángulo de 360 ° corresponde al ángulo subtendido por un círculo completo y es igual a 2 π radianes, o 400 gradianes.
Otras unidades utilizadas para representar ángulos se enumeran en la siguiente tabla. Estas unidades se definen de manera que el número de vueltas equivale a un círculo completo.
| nombre | número en un turno | Ángulo de rotación | descripción |
|---|---|---|---|
| Girar | 1 | 360 ° | El giro , también ciclo , círculo completo , revolución y rotación , es movimiento circular completo o medida (como para volver al mismo punto) con círculo o elipse. Un giro se abrevia τ , cyc , rev o rot dependiendo de la aplicación. El símbolo τ también se puede usar como una constante matemática para representar 2 π radianes. |
| Múltiplos de π | 2 | 180 ° | La unidad de múltiplos de π (MUL π ) se implementa en la calculadora científica RPN WP 43S . Consulte también: operaciones recomendadas por IEEE 754 |
| Cuadrante | 4 | 90 ° | Un cuadrante es un1/4 giro y también conocido como ángulo recto . El cuadrante es la unidad utilizada en Elementos de Euclides . En alemán, el símbolo ∟ se ha utilizado para indicar un cuadrante. Es la unidad utilizada en Elementos de Euclides . 1 quad = 90 ° =π/2 rad = 1/4 giro = 100 grad. |
| Sextante | 6 | 60 ° | El sextante era la unidad utilizada por los babilonios . El grado, minuto de arco y segundo de arco son subunidades sexagesimales de la unidad babilónica. Es especialmente fácil de construir con regla y brújula. Es el ángulo del triángulo equilátero o es1/6 girar. 1 unidad babilónica = 60 ° = π / 3 rad ≈ 1.047197551 rad. |
| Radián | 2 π | 57 ° 17 ′ | El radián está determinado por la circunferencia de un círculo que tiene la misma longitud que el radio del círculo ( n = 2 π = 6.283 ...). Es el ángulo subtendido por un arco de un círculo que tiene la misma longitud que el radio del círculo. El símbolo de radianes es rad . Un turno es 2 π radianes y un radianes es180 °/π, o alrededor de 57,2958 grados. En los textos matemáticos, los ángulos a menudo se tratan como adimensionales con el radianes igual a uno, lo que hace que la unidad rad se omita a menudo. El radianes se utiliza en prácticamente todo el trabajo matemático más allá de la geometría práctica simple, debido, por ejemplo, a las propiedades agradables y "naturales" que muestran las funciones trigonométricas cuando sus argumentos están en radianes. El radianes es la unidad (derivada) de medida angular en el SI , que también trata el ángulo como adimensional. |
| Hexacontade | 60 | 6 ° | La hexacontade es una unidad utilizada por Eratosthenes . Es igual a 6 °, por lo que un giro completo se dividió en 60 hexacontades. |
| Grado binario | 256 | 1 ° 33'45 " | El grado binario , también conocido como radián binario (o brad ). El grado binario se usa en computación para que un ángulo se pueda representar de manera eficiente en un solo byte (aunque con precisión limitada). Otras medidas de ángulo utilizadas en computación pueden basarse en dividir un giro completo en 2 n partes iguales para otros valores de n .
Está 1/256 de una vuelta. |
| La licenciatura | 360 | 1 ° | Una ventaja de esta antigua subunidad sexagesimal es que muchos ángulos comunes en geometría simple se miden como un número entero de grados. Las fracciones de un grado pueden escribirse en notación decimal normal (por ejemplo, 3,5 ° para tres grados y medio), pero las subunidades sexagesimales "minuto" y "segundo" del sistema "grado-minuto-segundo" también se utilizan, especialmente para coordenadas geográficas y en astronomía y balística ( n = 360) El grado , denotado por un pequeño círculo superíndice (°), es 1/360 de vuelta, por lo que una vuelta es 360 °. En el caso de grados para la fórmula dada anteriormente, un grado de n = 360 ° unidades se obtiene estableciendo k =360 °/2 π. |
| Grad | 400 | 0 ° 54 ′ | El graduado , también llamado grado , gradian o gon . un ángulo recto equivale a 100 grados. Es una subunidad decimal del cuadrante. Un kilómetro históricamente se define como un centi -grad de arco a lo largo de un meridiano de la Tierra, por lo que el kilómetro es el análogo de decimal a la sexagesimal milla náutica ( n = 400). El graduado se utiliza principalmente en triangulación y levantamientos continentales . |
| Minuto de arco | 21,600 | 0 ° 1 ′ | El minuto de arco (o MOA , minuto de arco , o simplemente minuto ) es1/60de un grado. Una milla náutica se definió históricamente como un minuto de arco a lo largo de un gran círculo de la Tierra ( n = 21.600). El minuto de arco es1/60 de un grado = 1/21,600girar. Se denota por un solo primo (′). Por ejemplo, 3 ° 30 ′ es igual a 3 × 60 + 30 = 210 minutos o 3 + 30/60= 3,5 grados. A veces también se usa un formato mixto con fracciones decimales, por ejemplo, 3 ° 5.72 ′ = 3 + 5.72/60grados. Una milla náutica se definió históricamente como un minuto de arco a lo largo de un gran círculo de la Tierra. |
| Segundo de arco | 1.296.000 | 0 ° 0′1 ″ | El segundo de arco (o segundo de arco , o simplemente segundos ) es1/60 de un minuto de arco y 1/3600de un grado ( n = 1.296.000). El segundo de arco (o segundo de arco , o simplemente segundos ) es1/60 de un minuto de arco y 1/3600de un grado. Se denota con un número primo doble (″). Por ejemplo, 3 ° 7 ′ 30 ″ es igual a 3 +7/60 + 30/3600 grados o 3,125 grados. |
Otros descriptores
- Ángulo horario ( n = 24): El ángulo horario astronómico es1/24 girar. Dado que este sistema permite medir objetos que realizan un ciclo una vez al día (como la posición relativa de las estrellas), las subunidades sexagesimales se denominan minuto de tiempo y segundo de tiempo . Estos son distintos y 15 veces más grandes que los minutos y segundos de arco. 1 hora = 15 ° =π/12 rad = 1/6 quad = 1/24 turn = 16+2/3 graduado
- (Brújula) punto o viento ( n = 32): El punto , utilizado en la navegación , es1/32de una vuelta. 1 punto =1/8de un ángulo recto = 11,25 ° = 12,5 grad. Cada punto se subdivide en cuatro cuartos de punto, de modo que 1 turno equivale a 128 cuartos de punto.
- Pechus ( n = 144-180): El pechus era una unidad babilónica igual a aproximadamente 2 ° o 2+1/2°.
- Tau , el número de radianes en una vuelta (1 vuelta = τ rad), τ = 2 π .
- Chi, una antigua medida de ángulos china.
- Parte de diámetro ( n = 376,99 ...): La parte de diámetro (utilizada ocasionalmente en matemáticas islámicas) es1/60radián. Una "parte de diámetro" es aproximadamente 0,95493 °. Hay alrededor de 376.991 piezas de diámetro por vuelta.
- Millirradian y definiciones derivadas: El verdadero miliradian se define como una milésima de radianes, lo que significa que una rotación de un giro equivaldría exactamente a 2000π mil (o aproximadamente 6283,185 mil), y casi todas las miras de alcance para armas de fuego están calibradas según esta definición. Además, hay otras tres definiciones derivadas utilizadas para artillería y navegación que son aproximadamente iguales a un milirradiano. Según estas otras tres definiciones, una vuelta equivale exactamente a 6000, 6300 o 6400 mils, lo que equivale a abarcar el rango de 0,05625 a 0,06 grados (3,375 a 3,6 minutos). En comparación, el milirradiano verdadero es aproximadamente 0.05729578 grados (3.43775 minutos). Un " mil de la OTAN " se define como1/6400de un círculo. Al igual que con el milirradiano verdadero, cada una de las otras definiciones explota la propiedad útil de las subtensiones de mil, es decir, que el valor de un milirradiano es aproximadamente igual al ángulo subtendido por un ancho de 1 metro visto desde 1 km de distancia (2 π/6400 = 0.0009817… ≈ 1/1000).
- Akhnam y zam. En la antigua Arabia, un turno se subdividía en 32 Akhnam y cada akhnam se subdividía en 7 zam, de modo que un turno es 224 zam.
Ángulos positivos y negativos
Aunque la definición de la medida de un ángulo no apoya el concepto de ángulo negativo, con frecuencia es útil imponer una convención que permita que los valores angulares positivos y negativos representen orientaciones y / o rotaciones en direcciones opuestas con respecto a alguna referencia.
En un sistema de coordenadas cartesiano bidimensional , un ángulo se define típicamente por sus dos lados, con su vértice en el origen. El lado inicial está en el eje x positivo , mientras que el otro lado o lado terminal está definido por la medida del lado inicial en radianes, grados o vueltas. Con ángulos positivos que representan rotaciones hacia el eje y positivo y ángulos negativos que representan rotaciones hacia el eje y negativo . Cuando las coordenadas cartesianas están representadas por la posición estándar , definida por el eje x hacia la derecha y el eje y hacia arriba, las rotaciones positivas son en sentido antihorario y las rotaciones negativas son en sentido horario .
En muchos contextos, un ángulo de - θ es efectivamente equivalente a un ángulo de "una vuelta completa menos θ ". Por ejemplo, una orientación representada como -45 ° es efectivamente equivalente a una orientación representada como 360 ° - 45 ° o 315 °. Aunque la posición final es la misma, una rotación física (movimiento) de -45 ° no es lo mismo que una rotación de 315 ° (por ejemplo, la rotación de una persona sosteniendo una escoba descansando sobre un piso polvoriento dejaría huellas visualmente diferentes de regiones barridas en el suelo).
En la geometría tridimensional, "en el sentido de las agujas del reloj" y "en el sentido contrario a las agujas del reloj" no tienen un significado absoluto, por lo que la dirección de los ángulos positivos y negativos debe definirse en relación con alguna referencia, que suele ser un vector que pasa por el vértice del ángulo y es perpendicular al plano en donde se encuentran los rayos del ángulo.
En la navegación , los rumbos o acimut se miden con respecto al norte. Por convención, visto desde arriba, los ángulos de orientación son positivos en el sentido de las agujas del reloj, por lo que una orientación de 45 ° corresponde a una orientación noreste. Los rumbos negativos no se utilizan en la navegación, por lo que una orientación noroeste corresponde a un rumbo de 315 °.
Formas alternativas de medir el tamaño de un ángulo
Hay varias alternativas para medir el tamaño de un ángulo por el ángulo de rotación. La pendiente o gradiente es igual a la tangente del ángulo, o algunas veces (raramente) al seno ; un gradiente a menudo se expresa como un porcentaje. Para valores muy pequeños (menos del 5%), la pendiente de una pendiente es aproximadamente la medida del ángulo en radianes.
En geometría racional, la extensión entre dos líneas se define como el cuadrado del seno del ángulo entre las líneas. Como el seno de un ángulo y el seno de su ángulo suplementario son iguales, cualquier ángulo de rotación que asigne una de las líneas a la otra conduce al mismo valor para la extensión entre las líneas.
Aproximaciones astronómicas
Los astrónomos miden la separación angular de los objetos en grados desde su punto de observación.
- 0.5 ° es aproximadamente el ancho del sol o la luna.
- 1 ° es aproximadamente el ancho de un dedo meñique con el brazo extendido.
- 10 ° es aproximadamente el ancho de un puño cerrado con el brazo extendido.
- 20 ° es aproximadamente el ancho de un palmo con el brazo extendido.
Estas mediciones dependen claramente de la sujeto individual, y la de arriba deben ser tratados como áspera regla general sólo aproximaciones.
En astronomía , la ascensión recta y la declinación generalmente se miden en unidades angulares, expresadas en términos de tiempo, sobre la base de un día de 24 horas.
| Unidad | Símbolo | La licenciatura | Radianes | Circulo | Otro |
|---|---|---|---|---|---|
| Hora | h | 15 ° | π ⁄ 12 | 1 ⁄ 24 | |
| Minuto | metro | 0 ° 15 ' | π ⁄ 720 | 1 ⁄ 1.440 | 1 ⁄ 60 hora |
| Segundo | s | 0 ° 0'15 " | π ⁄ 43200 | 1 ⁄ 86,400 | 1 ⁄ 60 minuto |
Medidas que no son unidades angulares
No todas las medidas de ángulos son unidades angulares, para una medida angular, es definitorio que se cumple el postulado de la suma de ángulos .
Algunas medidas de ángulos donde el postulado de la suma de ángulos no se cumple incluyen:
Ángulos entre curvas
El ángulo entre una línea y una curva (ángulo mixto) o entre dos curvas que se cruzan (ángulo curvilíneo) se define como el ángulo entre las tangentes en el punto de intersección. Se han dado varios nombres (ahora raramente, si alguna vez se usan) a casos particulares: - anficírtico (gr. Ἀμφί , en ambos lados, κυρτός, convexo) o cissoidal (gr. Κισσός, ivy), biconvexo; xystroidal o sistroidal (del gr. ξυστρίς, una herramienta para raspar), cóncavo-convexo; anficoélico (del gr. κοίλη, un hueco) o angulus lunularis , bicóncavo.
Ángulos de bisección y trisección
Los antiguos matemáticos griegos sabían cómo bisecar un ángulo (dividirlo en dos ángulos de igual medida) usando solo un compás y una regla , pero solo podían trisecar ciertos ángulos. En 1837, Pierre Wantzel demostró que para la mayoría de los ángulos esta construcción no se puede realizar.
Producto escalar y generalizaciones
En el espacio euclidiano , el ángulo θ entre dos vectores euclidianas u y v se relaciona con su producto escalar y sus longitudes por la fórmula
Esta fórmula proporciona un método sencillo para encontrar el ángulo entre dos planos (o superficies curvas) de sus vectores normales y entre líneas oblicuas de sus ecuaciones vectoriales.
Producto Interno
Para definir ángulos en un espacio de producto interno real abstracto , reemplazamos el producto escalar euclidiano ( · ) por el producto interno , es decir
En un espacio de producto interno complejo , la expresión del coseno anterior puede dar valores no reales, por lo que se reemplaza con
o, más comúnmente, usando el valor absoluto, con
La última definición ignora la dirección de los vectores y, por lo tanto, describe el ángulo entre los subespacios unidimensionales y abarcados por los vectores y en consecuencia.
Ángulos entre subespacios
La definición del ángulo entre subespacios unidimensionales y dada por
en un espacio de Hilbert se puede extender a subespacios de cualquier dimensión finita. Dados dos subespacios , con , esto conduce a una definición de ángulos llamados ángulos canónicos o principales entre subespacios.
Ángulos en geometría riemanniana
En la geometría de Riemann , el tensor métrico se usa para definir el ángulo entre dos tangentes . Donde U y V son vectores tangentes y g ij son los componentes del tensor métrico G ,
Ángulo hiperbólico
Un ángulo hiperbólico es un argumento de una función hiperbólica al igual que el ángulo circular es el argumento de una función circular . La comparación se puede visualizar como el tamaño de las aberturas de un sector hiperbólico y un sector circular ya que las áreas de estos sectores corresponden a las magnitudes de los ángulos en cada caso. A diferencia del ángulo circular, el ángulo hiperbólico no tiene límites. Cuando las funciones circulares e hiperbólicas se ven como series infinitas en su argumento de ángulo, las circulares son simplemente formas de series alternas de las funciones hiperbólicas. Este tejido de los dos tipos de ángulo y función fue explicado por Leonhard Euler en Introducción al análisis del infinito .
Ángulos en geografía y astronomía
En geografía , la ubicación de cualquier punto de la Tierra se puede identificar mediante un sistema de coordenadas geográficas . Este sistema especifica la latitud y longitud de cualquier ubicación en términos de ángulos subtendidos en el centro de la Tierra, usando el ecuador y (generalmente) el meridiano de Greenwich como referencias.
En astronomía , un punto dado en la esfera celeste (es decir, la posición aparente de un objeto astronómico) se puede identificar usando cualquiera de varios sistemas de coordenadas astronómicas , donde las referencias varían según el sistema particular. Los astrónomos miden la separación angular de dos estrellas imaginando dos líneas a través del centro de la Tierra , cada una cruzando una de las estrellas. El ángulo entre esas líneas se puede medir y es la separación angular entre las dos estrellas.
Tanto en geografía como en astronomía, una dirección de observación se puede especificar en términos de un ángulo vertical , como la altitud / elevación con respecto al horizonte , así como el acimut con respecto al norte .
Los astrónomos también miden el tamaño aparente de los objetos como un diámetro angular . Por ejemplo, la luna llena tiene un diámetro angular de aproximadamente 0,5 °, cuando se ve desde la Tierra. Se podría decir: "El diámetro de la Luna subtiende un ángulo de medio grado". La fórmula de ángulo pequeño se puede utilizar para convertir dicha medida angular en una relación distancia / tamaño.
Ver también
- Instrumento de medición de ángulos
- Estadísticas angulares ( media , desviación estándar )
- Bisectriz
- Aceleración angular
- Diámetro angular
- Velocidad angular
- Argumento (análisis complejo)
- Aspecto astrológico
- Ángulo central
- Problema del ángulo del reloj
- Grados decimales
- Ángulo diedro
- Teorema del ángulo exterior
- Ángulo dorado
- Gran distancia circular
- Ángulo inscrito
- Ángulo irracional
- Fase (ondas)
- Transportador
- Ángulo sólido
- Ángulo esférico
- Ángulo trascendente
- Trisección
- Ángulo cenital
Notas
Referencias
Bibliografía
- Henderson, David W .; Taimina, Daina (2005), Experimentar la geometría / euclidiana y no euclidiana con la historia (3ª ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7
- Heiberg, Johan Ludvig (1908), Heath, TL (ed.), Euclid , The Thirteen Books of Euclid's Elements, 1 , Cambridge : Cambridge University Press.
- Sidorov, LA (2001) [1994], "Angle" , Encyclopedia of Mathematics , EMS Press
- Jacobs, Harold R. (1974), Geometría , WH Freeman, págs. 97, 255, ISBN 978-0-7167-0456-0
- Slocum, Jonathan (2007), Léxico indoeuropeo preliminar - Datos de Pokorny PIE , Departamento de investigación de la Universidad de Texas: centro de investigación lingüística , consultado el 2 de febrero de 2010
- Shute, William G .; Shirk, William W .; Porter, George F. (1960), Geometría plana y sólida , American Book Company, págs. 25-27
- Wong, Tak-wah; Wong, Ming-sim (2009), "Angles in Intersecting and Parallel Lines", New Century Mathematics , 1B (1 ed.), Hong Kong: Oxford University Press, págs. 161-163, ISBN 978-0-19-800177-5
Este artículo incorpora texto de una publicación que ahora es de dominio público : Chisholm, Hugh, ed. (1911), " Angle ", Encyclopædia Britannica , 2 (11ª ed.), Cambridge University Press, pág. 14
enlaces externos
- , Encyclopædia Britannica , 2 (9ª ed.), 1878, págs. 29-30




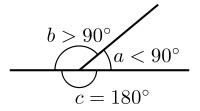

![{\ Displaystyle {\ begin {alineado} & \ sin ^ {2} A + \ sin ^ {2} B = 1 && \ cos ^ {2} A + \ cos ^ {2} B = 1 \\ [3pt] & \ tan A = \ cot B && \ sec A = \ csc B \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)