Polígono regular - Regular polygon

Conjunto de n-gons regulares convexos
Polígonos regulares
Aristas y vértices	norte
Símbolo de Schläfli	{ n }
Diagrama de Coxeter-Dynkin
Grupo de simetría	D n , orden 2n
Polígono dual	Auto-dual
Área (con longitud lateral, s )	${\ Displaystyle A = {\ tfrac {1} {4}} ns ^ {2} \ cot \ left ({\ frac {\ pi} {n}} \ right)}$
Ángulo interno	${\ Displaystyle (n-2) \ times {\ frac {180 ^ {\ circ}} {n}}}$
Suma de ángulos internos	${\ Displaystyle \ left (n-2 \ right) \ times 180 ^ {\ circ}}$
Diámetro del círculo inscrito	${\ Displaystyle d _ {\ text {IC}} = s \ cot \ left ({\ frac {\ pi} {n}} \ right)}$
Diámetro del círculo circunscrito	${\ Displaystyle d _ {\ text {OC}} = s \ csc \ left ({\ frac {\ pi} {n}} \ right)}$
Propiedades	Convexo , cíclico , equilátero , isogonal , isotoxal

En geometría euclidiana , un polígono regular es un polígono que es equiangular (todos los ángulos son iguales en medida) y equilátero (todos los lados tienen la misma longitud). Los polígonos regulares pueden ser convexos o en estrella . En el límite , una secuencia de polígonos regulares con un número creciente de lados se aproxima a un círculo , si el perímetro o área es fijo, o un apeirogon regular (efectivamente una línea recta ), si la longitud del borde es fija.

Propiedades generales

Polígonos regulares convexos y en estrella con 3 a 12 vértices etiquetados con sus símbolos de Schläfli

Estas propiedades se aplican a todos los polígonos regulares, ya sean convexos o en estrella .

Un polígono regular de n lados tiene una simetría rotacional de orden n .

Todos los vértices de un polígono regular se encuentran en un círculo común (el círculo circunscrito ); es decir, son puntos concíclicos . Es decir, un polígono regular es un polígono cíclico .

Junto con la propiedad de los lados de igual longitud, esto implica que cada polígono regular también tiene un círculo inscrito o incircle que es tangente a cada lado en el punto medio. Por tanto, un polígono regular es un polígono tangencial .

Se puede construir un polígono regular de n lados con compás y regla no graduada si y solo si los factores primos impares de n son primos de Fermat distintos . Ver polígono construible .

Simetría

El grupo de simetría de un polígono regular de n lados es el grupo diedro D _n (de orden 2 n ): D ₂ , D ₃ , D ₄ , ... Consiste en las rotaciones en C _n , junto con la simetría de reflexión en n ejes que pasan por el centro. Si n es par, la mitad de estos ejes pasa por dos vértices opuestos y la otra mitad por el punto medio de los lados opuestos. Si n es impar, todos los ejes pasan por un vértice y el punto medio del lado opuesto.

Polígonos convexos regulares

Todos los polígonos simples regulares (un polígono simple es uno que no se cruza en ninguna parte) son convexos. Los que tienen el mismo número de lados también son similares .

Un polígono regular convexo de n lados se denota por su símbolo de Schläfli { n }. Para n <3, tenemos dos casos degenerados :

Monogon {1}

Degenerado en el espacio ordinario . (La mayoría de las autoridades no consideran el monogon como un verdadero polígono, en parte debido a esto, y también porque las fórmulas siguientes no funcionan, y su estructura no es la de ningún polígono abstracto ).

Digon {2}; un "segmento de doble línea"

Degenerado en el espacio ordinario . (Algunas autoridades no consideran el digón como un verdadero polígono debido a esto).

En determinados contextos todos los polígonos considerados serán regulares. En tales circunstancias, se acostumbra eliminar el prefijo regular. Por ejemplo, todas las caras de los poliedros uniformes deben ser regulares y las caras se describirán simplemente como triángulo, cuadrado, pentágono, etc.

Anglos

Para un n -gon convexo regular , cada ángulo interior tiene una medida de:

${\ Displaystyle {\ frac {180 (n-2)} {n}}}$ grados;

${\ Displaystyle {\ frac {(n-2) \ pi} {n}}}$radianes; o

${\ Displaystyle {\ frac {(n-2)} {2n}}}$vueltas completas ,

y cada ángulo exterior (es decir, suplementario al ángulo interior) tiene una medida de grados, con la suma de los ángulos exteriores igual a 360 grados o 2π radianes o una vuelta completa. ${\ Displaystyle {\ tfrac {360} {n}}}$

Cuando n se acerca al infinito, el ángulo interno se acerca a 180 grados. Para un polígono regular con 10,000 lados (un miriagón ), el ángulo interno es 179.964 °. A medida que aumenta el número de lados, el ángulo interno puede acercarse mucho a 180 ° y la forma del polígono se acerca a la de un círculo. Sin embargo, el polígono nunca puede convertirse en un círculo. El valor del ángulo interno nunca puede llegar a ser exactamente igual a 180 °, ya que la circunferencia se convertiría efectivamente en una línea recta. Por esta razón, un círculo no es un polígono con un número infinito de lados.

Diagonales

Para n > 2, el número de diagonales es ; es decir, 0, 2, 5, 9, ..., para un triángulo, cuadrado, pentágono, hexágono, .... Las diagonales dividen el polígono en 1, 4, 11, 24, ... piezas OEIS :  A007678 . ${\ Displaystyle {\ tfrac {1} {2}} n (n-3)}$

Para un n -gon regular inscrito en un círculo de radio unitario, el producto de las distancias desde un vértice dado a todos los demás vértices (incluidos los vértices adyacentes y los vértices conectados por una diagonal) es igual a n .

Puntos en el plano

Para un n -gon regular simple con circunradio R y distancias d _i desde un punto arbitrario en el plano a los vértices, tenemos

${\ Displaystyle {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} d_ {i} ^ {4} + 3R ^ {4} = \ left ({\ frac {1} { n}} \ sum _ {i = 1} ^ {n} d_ {i} ^ {2} + R ^ {2} \ right) ^ {2}.}$

Para potencias superiores de distancias desde un punto arbitrario en el plano hasta los vértices de un -gon regular , si ${\ Displaystyle d_ {i}}$${\ Displaystyle n}$

${\ Displaystyle S_ {n} ^ {(2m)} = {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} d_ {i} ^ {2m}}$,

luego

${\ Displaystyle S_ {n} ^ {(2m)} = \ left (S_ {n} ^ {(2)} \ right) ^ {m} + \ sum _ {k = 1} ^ {\ left \ lfloor { \ frac {m} {2}} \ right \ rfloor} {\ binom {m} {2k}} {\ binom {2k} {k}} R ^ {2k} \ left (S_ {n} ^ {(2 )} - R ^ {2} \ right) ^ {k} \ left (S_ {n} ^ {(2)} \ right) ^ {m-2k}}$,

y

${\ Displaystyle S_ {n} ^ {(2m)} = \ left (S_ {n} ^ {(2)} \ right) ^ {m} + \ sum _ {k = 1} ^ {\ left \ lfloor { \ frac {m} {2}} \ right \ rfloor} {\ frac {1} {2 ^ {k}}} {\ binom {m} {2k}} {\ binom {2k} {k}} \ left (S_ {n} ^ {(4)} - \ left (S_ {n} ^ {(2)} \ right) ^ {2} \ right) ^ {k} \ left (S_ {n} ^ {(2 )} \ right) ^ {m-2k}}$,

donde es un número entero positivo menor que . ${\ Displaystyle m}$${\ Displaystyle n}$

Si es la distancia desde un punto arbitrario en el plano al centroide de un -gon regular con circunradio , entonces ${\ Displaystyle L}$${\ Displaystyle n}$${\ Displaystyle R}$

${\ Displaystyle \ sum _ {i = 1} ^ {n} d_ {i} ^ {2m} = n \ left (\ left (R ^ {2} + L ^ {2} \ right) ^ {m} + \ sum _ {k = 1} ^ {\ left \ lfloor {\ frac {m} {2}} \ right \ rfloor} {\ binom {m} {2k}} {\ binom {2k} {k}} R ^ {2k} L ^ {2k} \ left (R ^ {2} + L ^ {2} \ right) ^ {m-2k} \ right)}$,

donde = 1, 2,… ,. ${\ Displaystyle m}$${\ Displaystyle n-1}$

Puntos interiores

Para un n -gon regular , la suma de las distancias perpendiculares desde cualquier punto interior a los n lados es n veces la apotema (la apotema es la distancia desde el centro a cualquier lado). Ésta es una generalización del teorema de Viviani para el caso n = 3.

Circumradius

Pentágono regular ( n = 5) con lado s , circunradio R y apotema a

Gráficos de lado ,  s ; apotema ,  a ; y área ,  A de polígonos regulares de n lados y circunradio 1, con la base ,  b de un rectángulo con la misma área . La línea verde muestra el caso n = 6 .

La circunferencia circunscrita R desde el centro de un polígono regular a uno de los vértices se relaciona con la longitud del lado s o a la apotema una por

${\ Displaystyle R = {\ frac {s} {2 \ sin \ left ({\ frac {\ pi} {n}} \ right)}} = {\ frac {a} {\ cos \ left ({\ frac {\ pi} {n}} \ derecha)}}}$

Para polígonos construibles , existen expresiones algebraicas para estas relaciones; ver Polígono bicéntrico # Polígonos regulares .

La suma de las perpendiculares desde los vértices de un n -gon regular hasta cualquier línea tangente al circunferencial es igual a n veces el circunradio.

La suma de las distancias al cuadrado desde los vértices de un n -gon regular hasta cualquier punto de su circunferencia es igual a 2 nR ² donde R es la circunferencia.

La suma de las distancias al cuadrado desde los puntos medios de los lados de un n -gon regular hasta cualquier punto de la circunferencia es 2 nR ² -1/4ns ² , donde s es la longitud del lado y R es el circunradio.

Si son las distancias desde los vértices de un -gon regular hasta cualquier punto de su circunferencia, entonces ${\ Displaystyle d_ {i}}$${\ Displaystyle n}$

${\ Displaystyle 3 \ left (\ sum _ {i = 1} ^ {n} d_ {i} ^ {2} \ right) ^ {2} = 2n \ sum _ {i = 1} ^ {n} d_ { i} ^ {4}}$.

Disecciones

Coxeter afirma que cada zonogon (un gon de 2 m cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en o${\ Displaystyle {\ tbinom {n} {2}}}$1/2m ( m - 1) paralelogramos. Estos mosaicos están contenidos como subconjuntos de vértices, aristas y caras en proyecciones ortogonales m -cubos . En particular, esto es cierto para los polígonos regulares con muchos lados iguales, en cuyo caso los paralelogramos son todos rombos. La lista OEIS :  A006245 da el número de soluciones para polígonos más pequeños.

Disecciones de ejemplo para polígonos regulares de lados pares seleccionados

2 m	6	8	10	12	14	dieciséis	18	20	24	30	40	50
Imagen
Rombos	3	6	10	15	21	28	36	45	66	105	190	300

Zona

El área A de un polígono convexo regular de n lados que tiene lados s , circunradio R , apotema a y perímetro p está dado por

${\ Displaystyle A = {\ tfrac {1} {2}} nsa = {\ tfrac {1} {2}} pa = {\ tfrac {1} {4}} ns ^ {2} \ cot \ left ({ \ tfrac {\ pi} {n}} \ right) = na ^ {2} \ tan \ left ({\ tfrac {\ pi} {n}} \ right) = {\ tfrac {1} {2}} nR ^ {2} \ sin \ left ({\ tfrac {2 \ pi} {n}} \ right)}$

Para polígonos regulares con lado s = 1, circunradio R = 1 o apotema a = 1, esto produce la siguiente tabla: (Tenga en cuenta que dado${\ Displaystyle \ cot x \ rightarrow 1 / x}$${\ displaystyle x \ rightarrow 0}$ que as , el área cuando tiende a as crece). ${\ Displaystyle s = 1}$${\ Displaystyle n ^ {2} / 4 \ pi}$${\ Displaystyle n}$

Numero de lados	Área cuando el lado s = 1		Área cuando circunradio R = 1			Área cuando apotema a = 1
	Exacto	Aproximación	Exacto	Aproximación	Relativo al área de circunferencia	Exacto	Aproximación	Relativo al área del círculo
norte	${\ Displaystyle {\ tfrac {n} {4}} \ cot \ left ({\ tfrac {\ pi} {n}} \ right)}$		${\ Displaystyle {\ tfrac {n} {2}} \ sin \ left ({\ tfrac {2 \ pi} {n}} \ right)}$		${\ Displaystyle {\ tfrac {n} {2 \ pi}} \ sin \ left ({\ tfrac {2 \ pi} {n}} \ right)}$	${\ Displaystyle n \ tan \ left ({\ tfrac {\ pi} {n}} \ right)}$		${\ Displaystyle {\ tfrac {n} {\ pi}} \ tan \ left ({\ tfrac {\ pi} {n}} \ right)}$
3	${\ Displaystyle {\ tfrac {\ sqrt {3}} {4}}}$	0,433012702	${\ Displaystyle {\ tfrac {3 {\ sqrt {3}}} {4}}}$	1.299038105	0,4134966714	${\ Displaystyle 3 {\ sqrt {3}}}$	5.196152424	1,653986686
4	1	1.000000000	2	2.000000000	0,6366197722	4	4.000000000	1.273239544
5	${\ Displaystyle {\ tfrac {1} {4}} {\ sqrt {25 + 10 {\ sqrt {5}}}}}$	1.720477401	${\ Displaystyle {\ tfrac {5} {4}} {\ sqrt {{\ tfrac {1} {2}} \ left (5 + {\ sqrt {5}} \ right)}}}$	2.377641291	0,7568267288	${\ Displaystyle 5 {\ sqrt {5-2 {\ sqrt {5}}}}}$	3.632712640	1.156328347
6	${\ Displaystyle {\ tfrac {3 {\ sqrt {3}}} {2}}}$	2.598076211	${\ Displaystyle {\ tfrac {3 {\ sqrt {3}}} {2}}}$	2.598076211	0,8269933428	${\ Displaystyle 2 {\ sqrt {3}}}$	3.464101616	1.102657791
7		3.633912444		2.736410189	0.8710264157		3.371022333	1.073029735
8	${\ Displaystyle 2 + 2 {\ sqrt {2}}}$	4.828427125	${\ Displaystyle 2 {\ sqrt {2}}}$	2.828427125	0.9003163160	${\ Displaystyle 8 \ left ({\ sqrt {2}} - 1 \ right)}$	3.313708500	1.054786175
9		6.181824194		2.892544244	0,9207254290		3.275732109	1.042697914
10	${\ Displaystyle {\ tfrac {5} {2}} {\ sqrt {5 + 2 {\ sqrt {5}}}}}$	7.694208843	${\ Displaystyle {\ tfrac {5} {2}} {\ sqrt {{\ tfrac {1} {2}} \ left (5 - {\ sqrt {5}} \ right)}}}$	2.938926262	0,9354892840	${\ Displaystyle 2 {\ sqrt {25-10 {\ sqrt {5}}}}}$	3.249196963	1.034251515
11		9.365639907		2.973524496	0,9465022440		3.229891423	1.028106371
12	${\ Displaystyle 6 + 3 {\ sqrt {3}}}$	11.19615242	3	3.000000000	0,9549296586	${\ Displaystyle 12 \ left (2 - {\ sqrt {3}} \ right)}$	3.215390309	1.023490523
13		13.18576833		3.020700617	0.9615188694		3.204212220	1.019932427
14		15.33450194		3.037186175	0,9667663859		3.195408642	1.017130161
15		17.64236291		3.050524822	0,9710122088		3.188348426	1.014882824
dieciséis		20.10935797	${\ Displaystyle 4 {\ sqrt {2 - {\ sqrt {2}}}}}$	3.061467460	0,9744953584		3.182597878	1.013052368
17		22.73549190		3.070554163	0,9773877456		3.177850752	1.011541311
18		25.52076819		3.078181290	0.9798155361		3.173885653	1.010279181
19		28.46518943		3.084644958	0,9818729854		3.170539238	1.009213984
20		31.56875757		3.090169944	0,9836316430		3.167688806	1.008306663
100		795.5128988		3.139525977	0,9993421565		3.142626605	1.000329117
1000		79577.20975		3.141571983	0,9999934200		3.141602989	1,000003290
10,000		7957746.893		3.141592448	0,9999999345		3.141592757	1.000000033
1.000.000		79577471545		3.141592654	1.000000000		3.141592654	1.000000000

Comparación de tamaños de polígonos regulares con la misma longitud de borde, de tres a sesenta lados. El tamaño aumenta sin límite a medida que el número de lados se acerca al infinito.

De todas n -gons con un perímetro dado, el que tiene la mayor superficie es regular.

Polígono construible

Algunos polígonos regulares son fáciles de construir con brújula y regla ; otros polígonos regulares no se pueden construir en absoluto. Los antiguos matemáticos griegos sabían cómo construir un polígono regular con 3, 4 o 5 lados, y sabían cómo construir un polígono regular con el doble de lados de un polígono regular dado. Esto llevó a la pregunta planteada ser: ¿es posible construir todos los regulares n -gons con regla y compás? Si no es así, ¿qué n- gones son construibles y cuáles no?

Carl Friedrich Gauss demostró la constructibilidad del 17-gon regular en 1796. Cinco años más tarde, desarrolló la teoría de los períodos gaussianos en sus Disquisitiones Arithmeticae . Esta teoría le permitió formular una condición suficiente para la constructibilidad de polígonos regulares:

Se puede construir un n -gon regular con compás y regla si n es el producto de una potencia de 2 y cualquier número de números primos de Fermat distintos (incluido ninguno).

(Un número primo de Fermat es un número primo de la forma ) Gauss declaró sin pruebas que esta condición también era necesaria , pero nunca publicó su prueba. Pierre Wantzel dio una prueba completa de la necesidad en 1837. El resultado se conoce como el teorema de Gauss-Wantzel . ${\ Displaystyle 2 ^ {(2 ^ {n})} + 1.}$

De manera equivalente, un n -gon regular es construible si y solo si el coseno de su ángulo común es un número construible , es decir, puede escribirse en términos de las cuatro operaciones aritméticas básicas y la extracción de raíces cuadradas.

Polígonos de sesgo regulares

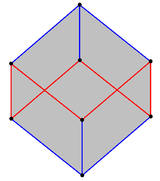El cubo contiene un hexágono regular inclinado , visto como 6 bordes rojos en zig-zag entre dos planos perpendiculares al eje diagonal del cubo.

Los bordes laterales en zig-zag de una n - antiprisma representan un sesgo 2 regular de n -gon, como se muestra en este antiprisma 17-gonal.

Un polígono sesgado regular en el espacio tridimensional puede verse como trayectorias no planas que zigzaguean entre dos planos paralelos, definidos como los bordes laterales de un antiprisma uniforme . Todos los bordes y ángulos internos son iguales.

Los sólidos platónicos ( tetraedro , cubo , octaedro , dodecaedro e icosaedro ) tienen polígonos de Petrie, que se ven en rojo aquí, con lados 4, 6, 6, 10 y 10 respectivamente.

De manera más general, los polígonos de sesgo regulares se pueden definir en n- espacio. Los ejemplos incluyen los polígonos de Petrie , caminos poligonales de bordes que dividen un politopo regular en dos mitades y se ven como un polígono regular en proyección ortogonal.

En el límite infinito, los polígonos de sesgo regulares se convierten en simétricos de sesgo .

Polígonos de estrella regulares

Polígonos de estrella regulares

2 <2q <p, mcd (p, q) = 1 {5/2} {7/2} {7/3} ...
Símbolo de Schläfli	{p / q}
Vértices y aristas	pag
Densidad	q
Diagrama de Coxeter
Grupo de simetría	Diedro (D p )
Polígono dual	Auto-dual
Ángulo interno ( grados )	${\ Displaystyle {\ frac {180 (p-2q)} {p}}}$

Un polígono regular no convexo es un polígono en estrella regular . El ejemplo más común es el pentagrama , que tiene los mismos vértices que un pentágono , pero conecta vértices alternos.

Para un polígono de estrellas de n lados, el símbolo de Schläfli se modifica para indicar la densidad o "estrellado" m del polígono, como { n / m }. Si m es 2, por ejemplo, entonces se une cada segundo punto. Si m es 3, entonces se une uno de cada tres puntos. El límite del polígono gira alrededor del centro m veces.

Las estrellas regulares (no degeneradas) de hasta 12 lados son:

• Pentagrama : {5/2}
• Heptagrama : {7/2} y {7/3}
• Octagrama : {8/3}
• Eneagrama - {9/2} y {9/4}
• Decagramo - {10/3}
• Hendecagram : {11/2}, {11/3}, {11/4} y {11/5}
• Dodecagrama : {12/5}

m y n debe ser primos entre sí , o la figura degenerará.

Las estrellas regulares degeneradas de hasta 12 lados son:

• Tetragón - {4/2}
• Hexágonos: {6/2}, {6/3}
• Octágonos: {8/2}, {8/4}
• Eneagon - {9/3}
• Decágonos: {10/2}, {10/4} y {10/5}
• Dodecágonos: {12/2}, {12/3}, {12/4} y {12/6}

Dos interpretaciones de {6/2}

Grünbaum {6/2} o 2 {3}	Coxeter 2 {3} o {6} [2 {3}] {6}
Hexágono de doble herida	Hexagrama como compuesto de dos triángulos

Dependiendo de la derivación precisa del símbolo Schläfli, las opiniones difieren en cuanto a la naturaleza de la figura degenerada. Por ejemplo, {6/2} puede tratarse de dos formas:

• Durante gran parte del siglo XX (ver, por ejemplo, Coxeter (1948) ), comúnmente hemos tomado / 2 para indicar unir cada vértice de un convexo {6} a sus vecinos cercanos a dos pasos de distancia, para obtener el compuesto regular de dos triángulos. o hexagrama .
  Coxeter aclara este compuesto regular con una notación {kp} [k {p}] {kp} para el compuesto {p / k}, por lo que el hexagrama se representa como {6} [2 {3}] {6}. De manera más compacta, Coxeter también escribe 2 {n / 2}, como 2 {3} para un hexagrama compuesto como alternancia de polígonos regulares de lados pares, con cursiva en el factor principal para diferenciarlo de la interpretación coincidente.
• Muchos geómetras modernos, como Grünbaum (2003), consideran esto incorrecto. Toman / 2 para indicar que se mueven dos lugares alrededor de {6} en cada paso, obteniendo un triángulo de "doble herida" que tiene dos vértices superpuestos en cada punto de esquina y dos bordes a lo largo de cada segmento de línea. Esto no solo encaja mejor con las teorías modernas de los politopos abstractos , sino que también copia más fielmente la forma en que Poinsot (1809) creó sus polígonos estelares, tomando un solo tramo de alambre y doblándolo en puntos sucesivos a través del mismo ángulo. hasta que la figura se cerró.

Dualidad de polígonos regulares

Todos los polígonos regulares son auto-duales para la congruencia, y para n impares son auto-duales para la identidad.

Además, las figuras de estrellas regulares (compuestos), al estar compuestas por polígonos regulares, también son auto-duales.

Polígonos regulares como caras de poliedros

Un poliedro uniforme tiene polígonos regulares como caras, de modo que por cada dos vértices hay un mapeo de isometría uno en el otro (tal como lo hay para un polígono regular).

Un poliedro cuasirregular es un poliedro uniforme que tiene solo dos tipos de caras alternadas alrededor de cada vértice.

Un poliedro regular es un poliedro uniforme que tiene un solo tipo de cara.

Los poliedros convexos restantes (no uniformes) con caras regulares se conocen como sólidos de Johnson .

Un poliedro que tiene triángulos regulares como caras se llama deltaedro .

Ver también

• Mosaicos euclidianos por polígonos regulares convexos
• Sólido platónico
• Apeirogon : un polígono de lados infinitos también puede ser regular, {∞}.
• Lista de politopos y compuestos regulares
• Polígono equilátero
• Círculo de Carlyle

Notas

Referencias

• Coxeter, HSM (1948). "Politopos regulares". Methuen y Co. Cite journal requiere |journal=( ayuda )
• Grünbaum, B .; ¿Son tus poliedros iguales a mis poliedros ?, Discretos y comput. geom: el festschrift de Goodman-Pollack , Ed. Aronov y col., Springer (2003), págs. 461–488.
• Poinsot, L .; Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9 (1810), págs. 16–48.

enlaces externos

• Weisstein, Eric W. "Polígono regular" . MathWorld .
• Descripción del polígono regular con animación interactiva
• Circunferencia de un polígono regular con animación interactiva
• Área de un polígono regular Tres fórmulas diferentes, con animación interactiva
• Construcciones de artistas del Renacimiento de polígonos regulares en Convergence