Teorema fundamental de la teoría de Galois - Fundamental theorem of Galois theory

En matemáticas , el teorema fundamental de la teoría de Galois es un resultado que describe la estructura de ciertos tipos de extensiones de campo en relación a grupos . Évariste Galois lo demostró en su desarrollo de la teoría de Galois .

En su forma más básica, el teorema afirma que dada una extensión de campo E / F que es finita y Galois , existe una correspondencia uno a uno entre sus campos intermedios y subgrupos de su grupo de Galois . ( Los campos intermedios son campos K que satisfacen F ⊆ K ⊆ E ; también se denominan subextensiones de E / F ).

Descripción explícita de la correspondencia

Para extensiones finitas, la correspondencia se puede describir explícitamente como sigue.

• Para cualquier subgrupo H de Gal ( E / F ), el correspondiente campo fijo , denotado E ^H , es el conjunto de los elementos de E que están fijados por cada automorphism en H .
• Para cualquier campo intermedio K de E / F , el subgrupo correspondiente es Aut ( E / K ), es decir, el conjunto de esos automorfismos en Gal ( E / F ) que fijan cada elemento de K .

El teorema fundamental dice que esta correspondencia es una correspondencia uno a uno si (y solo si) E / F es una extensión de Galois . Por ejemplo, el campo superior E corresponde al subgrupo trivial de Gal ( E / F ), y el campo base F corresponde a todo el grupo Gal ( E / F ).

La notación Gal ( E / F ) solo se usa para extensiones de Galois . Si E / F es Galois, entonces Gal ( E / F ) = Aut ( E / F ). Si E / F no es Galois, entonces la "correspondencia" da sólo un mapa inyectivo (pero no sobreyectivo ) de a , y un mapa sobreyectivo (pero no inyectivo) en la dirección inversa. En particular, si E / F no es Galois, entonces F no es el campo fijo de ningún subgrupo de Aut ( E / F ). ${\ Displaystyle \ {{\ text {subgrupos de Aut}} (E / F) \}}$${\ Displaystyle \ {{\ text {subcampos de}} E / F \}}$

Propiedades de la correspondencia

La correspondencia tiene las siguientes propiedades útiles.

• Es inclusión-reversión . La inclusión de subgrupos H ₁ ⊆ H _{2 se} cumple si y solo si se cumple la inclusión de los campos E ^{H ₁} ⊇ E ^{H ₂} .
• Los grados de extensión están relacionados con órdenes de grupos, de una manera consistente con la propiedad de inversión de inclusión. Específicamente, si H es un subgrupo de Gal ( E / F ), entonces | H | = [ E : E ^H ] y | Gal ( E / F ) | / | H | = [ E ^H : F ].
• El campo E ^H es una extensión normal de F (o, de manera equivalente, extensión de Galois, ya que cualquier subextensión de una extensión separable es separable) si y solo si H es un subgrupo normal de Gal ( E / F ). En este caso, la restricción de los elementos de Gal ( E / F ) a E ^H induce un isomorfismo entre Gal ( E ^H / F ) y el grupo cociente Gal ( E / F ) / H .

Ejemplo 1

Considere el campo

${\ Displaystyle K = \ mathbb {Q} \ left ({\ sqrt {2}}, {\ sqrt {3}} \ right) = \ left [\ mathbb {Q} ({\ sqrt {2}}) \ derecha] \! ({\ sqrt {3}}).}$

Dado que K se construye a partir del campo base al unir √ 2 , luego √ 3 , cada elemento de K se puede escribir como: ${\ Displaystyle \ mathbb {Q}}$

${\ Displaystyle (a + b {\ sqrt {2}}) + (do + d {\ sqrt {2}}) {\ sqrt {3}}, \ qquad a, b, c, d \ in \ mathbb { Q}.}$

Su grupo de Galois comprende los automorfismos de K que fijan a . Estos automorfismos deben enviar √ 2 a √ 2 o - √ 2 , y enviar √ 3 a √ 3 o - √ 3 , ya que permutan las raíces de cualquier polinomio irreducible. Suponga que f intercambia √ 2 y - √ 2 , entonces ${\ Displaystyle G = {\ text {Gal}} (K / \ mathbb {Q})}$

${\ Displaystyle f \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (ab {\ sqrt {2 }}) + (cd {\ sqrt {2}}) {\ sqrt {3}} = ab {\ sqrt {2}} + c {\ sqrt {3}} - d {\ sqrt {6}},}$

y g intercambios √ 3 y - √ 3 , por lo

${\ Displaystyle g \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (a + b {\ sqrt {2}}) - (c + d {\ sqrt {2}}) {\ sqrt {3}} = a + b {\ sqrt {2}} - c {\ sqrt {3}} - d {\ sqrt {6}}.}$

Se trata claramente de automorfismos de K , respetando su suma y multiplicación. También está el automorfismo de identidad e que fija cada elemento, y la composición de f y g que cambia los signos en ambos radicales:

${\ Displaystyle (fg) \ left ((a + b {\ sqrt {2}}) + (c + d {\ sqrt {2}}) {\ sqrt {3}} \ right) = (ab {\ sqrt {2}}) - (cd {\ sqrt {2}}) {\ sqrt {3}} = ab {\ sqrt {2}} - c {\ sqrt {3}} + d {\ sqrt {6}} .}$

Dado que el orden del grupo de Galois es igual al grado de extensión del campo , no puede haber más automorfismos: ${\ Displaystyle | G | = [K: \ mathbb {Q}] = 4}$

${\ Displaystyle G = \ left \ {1, f, g, fg \ right \},}$

que es isomorfo a los cuatro grupos de Klein . Sus cinco subgrupos corresponden a los campos intermedios entre la base y la extensión K . ${\ Displaystyle \ mathbb {Q}}$

• El subgrupo trivial {1} corresponde a todo el campo de extensión K .
• Todo el grupo G corresponde al campo base ${\ Displaystyle \ mathbb {Q}.}$
• El subgrupo {1, f } corresponde al subcampo ya que f fija √ 3 . ${\ Displaystyle \ mathbb {Q} ({\ sqrt {3}}),}$
• El subgrupo {1, g } corresponde al subcampo ya que g fija √ 2 . ${\ Displaystyle \ mathbb {Q} ({\ sqrt {2}}),}$
• El subgrupo {1, fg } corresponde al subcampo ya que fg fija √ 6 . ${\ Displaystyle \ mathbb {Q} ({\ sqrt {6}}),}$

Ejemplo 2

El siguiente es el caso más simple en el que el grupo de Galois no es abeliano.

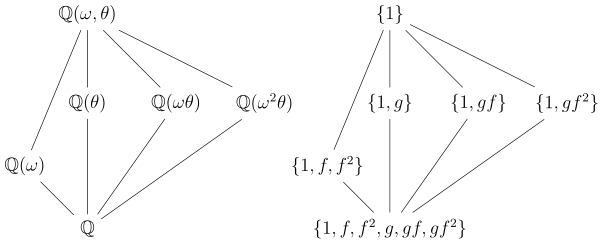
Considere el campo de división K del polinomio irreducible sobre ; es decir, donde θ es una raíz cúbica de 2 y ω es una raíz cúbica de 1 (pero no 1 en sí). Si consideramos K dentro de los números complejos, podemos tomar la raíz cúbica real de 2, y dado que ω tiene un polinomio mínimo , la extensión tiene grado: ${\ displaystyle x ^ {3} -2}$${\ Displaystyle \ mathbb {Q}}$${\ Displaystyle K = \ mathbb {Q} (\ theta, \ omega)}$${\ Displaystyle \ theta = {\ sqrt [{3}] {2}}}$${\ Displaystyle \ omega = - {\ tfrac {1} {2}} + i {\ tfrac {\ sqrt {3}} {2}}.}$${\ Displaystyle x ^ {2} + x + 1}$${\ Displaystyle \ mathbb {Q} \ subconjunto K}$

${\ Displaystyle [\, K: \ mathbb {Q} \,] = [\, K: \ mathbb {Q} [\, \ theta \,] \,] \ cdot [\, \ mathbb {Q} [\ , \ theta \,]: \ mathbb {Q} \,] = 2 \ cdot 3 = 6}$ ,

con -basis como en el ejemplo anterior. Por lo tanto, el grupo de Galois tiene seis elementos, determinados por permutaciones de las tres raíces de : ${\ Displaystyle \ mathbb {Q}}$${\ Displaystyle \ {1, \ theta, \ theta ^ {2}, \ omega, \ omega \ theta, \ omega \ theta ^ {2} \}}$${\ Displaystyle G = {\ text {Gal}} (K / \ mathbb {Q})}$${\ displaystyle x ^ {3} -2}$

${\ Displaystyle \ alpha _ {1} = \ theta, \ \ alpha _ {2} = \ omega \ theta, \ \ alpha _ {3} = \ omega ^ {2} \ theta.}$

¡Ya que solo hay 3! = 6 de tales permutaciones, G debe ser isomorfo al grupo simétrico de todas las permutaciones de tres objetos. El grupo puede ser generada por dos automorfismos f y g definidas por:

${\ Displaystyle f (\ theta) = \ omega \ theta, \ quad f (\ omega) = \ omega,}$

${\ Displaystyle g (\ theta) = \ theta, \ quad g (\ omega) = \ omega ^ {2},}$

y obedecer las relaciones . Su efecto como permutaciones de decir (en la notación ciclo ): . Además, g puede considerarse como el mapeo de conjugación complejo . ${\ Displaystyle G = \ left \ {1, f, f ^ {2}, g, gf, gf ^ {2} \ right \}}$${\ Displaystyle f ^ {3} = g ^ {2} = (gf) ^ {2} = 1}$${\ Displaystyle \ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3}}$${\ Displaystyle f = (123), g = (23)}$

Los subgrupos de G y los subcampos correspondientes son los siguientes:

• Como siempre, el grupo trivial {1} ​​corresponde a todo el campo K , mientras que todo el grupo G al campo base . ${\ Displaystyle \ mathbb {Q}}$
• El subgrupo único de orden 3, corresponde al subcampo de grado dos, ya que el subgrupo tiene índice dos en G : ie . Además, este subgrupo es normal, por lo que el subcampo es normal , siendo el campo de división de . Su grupo de Galois sobre el campo base es el grupo del cociente , donde [ g ] denota la clase lateral de g módulo H ; es decir, su único automorfismo no trivial es la conjugación compleja g . ${\ Displaystyle H = \ {1, f, f ^ {2} \}}$${\ Displaystyle \ mathbb {Q} (\ omega)}$${\ Displaystyle [\ mathbb {Q} (\ omega): \ mathbb {Q}] = {\ tfrac {| G |} {| H |}} = 2}$${\ Displaystyle \ mathbb {Q}}$${\ Displaystyle x ^ {2} + x + 1}$ ${\ Displaystyle G / H = \ {[1], [g] \}}$
• Hay tres subgrupos de orden 2, y que corresponden respectivamente a los subcampos Estos subcampos tienen grado 3 más desde los subgrupos tienen índice 3 en G . Los subgrupos son no normales en G , por lo que los subcampos son no Galois o normales sobre . De hecho, cada subcampo contiene solo una de las raíces , por lo que ninguna tiene automorfismos no triviales. ${\ Displaystyle \ {1, g \}, \ {1, gf \}}$${\ Displaystyle \ {1, gf ^ {2} \},}$${\ Displaystyle \ mathbb {Q} (\ theta), \ mathbb {Q} (\ omega \ theta), \ mathbb {Q} (\ omega ^ {2} \ theta).}$${\ Displaystyle \ mathbb {Q}}$ ${\ Displaystyle \ mathbb {Q}}$${\ Displaystyle \ alpha _ {1}, \ alpha _ {2}, \ alpha _ {3}}$

Ejemplo 3

Sea el campo de funciones racionales en el λ indeterminado , y considere el grupo de automorfismos: ${\ Displaystyle E = \ mathbb {Q} (\ lambda)}$

${\ Displaystyle G = \ left \ {\ lambda, {\ frac {1} {1- \ lambda}}, {\ frac {\ lambda -1} {\ lambda}}, {\ frac {1} {\ lambda }}, {\ frac {\ lambda} {\ lambda -1}}, 1- \ lambda \ right \} \ subset \ mathrm {Aut} (E);}$

aquí denotamos un automorfismo por su valor , de modo que . Este grupo es isomorfo a (ver: seis relaciones cruzadas ). Sea el campo fijo de , de modo que . ${\ Displaystyle \ phi: E \ a E}$${\ Displaystyle \ phi (\ lambda)}$${\ Displaystyle f (\ lambda) \ mapsto f (\ phi (\ lambda))}$${\ Displaystyle S_ {3}}$${\ Displaystyle F}$${\ Displaystyle G}$${\ Displaystyle {\ rm {Gal}} (E / F) = G}$

Si es un subgrupo de , entonces los coeficientes del polinomio ${\ Displaystyle H}$${\ Displaystyle G}$

${\ Displaystyle P (T): = \ prod _ {h \ in H} (Th) \ in E [T]}$

generar el campo fijo de . La correspondencia de Galois implica que cada subcampo de puede construirse de esta manera. Por ejemplo, para , el campo fijo es y si entonces el campo fijo es . El campo fijo de es el campo base donde j es la j -invariante escrita en términos de la función lambda modular : ${\ Displaystyle H}$${\ Displaystyle E / F}$${\ Displaystyle H = \ {\ lambda, 1- \ lambda \}}$${\ Displaystyle \ mathbb {Q} (\ lambda (1- \ lambda))}$${\ Displaystyle H = \ {\ lambda, {\ tfrac {1} {\ lambda}} \}}$${\ Displaystyle \ mathbb {Q} (\ lambda + {\ tfrac {1} {\ lambda}})}$${\ Displaystyle G}$${\ Displaystyle F = \ mathbb {Q} (j),}$

${\ displaystyle j = {\ frac {256 (1- \ lambda (1- \ lambda)) ^ {3}} {(\ lambda (1- \ lambda)) ^ {2}}} = {\ frac {256 (1- \ lambda + \ lambda ^ {2}) ^ {3}} {\ lambda ^ {2} (1- \ lambda) ^ {2}}} \.}$

Se pueden construir ejemplos similares para cada uno de los grupos de simetría de los sólidos platónicos, ya que estos también tienen acciones fieles en la línea proyectiva y en adelante . ${\ Displaystyle \ mathbb {P} ^ {1} (\ mathbb {C})}$${\ Displaystyle \ mathbb {C} (x)}$

Aplicaciones

El teorema clasifica los campos intermedios de E / F en términos de teoría de grupos . Esta traducción entre campos intermedios y subgrupos es clave para demostrar que la ecuación quíntica general no se puede resolver mediante radicales (ver el teorema de Abel-Ruffini ). Primero se determinan los grupos de Galois de extensiones de radicales (extensiones de la forma F (α) donde α es una raíz n -ésima de algún elemento de F ), y luego se usa el teorema fundamental para demostrar que las extensiones con solución corresponden a grupos con solución .

Teorías como la teoría de Kummer y la teoría de campos de clases se basan en el teorema fundamental.

Caso infinito

Dada una extensión algebraica infinita, todavía podemos definirla como Galois si es normal y separable. El problema que uno encuentra en el caso infinito es que la biyección en el teorema fundamental no se cumple ya que generalmente obtenemos demasiados subgrupos. Más precisamente, si tomamos cada subgrupo, en general podemos encontrar dos subgrupos diferentes que fijan el mismo campo intermedio. Por lo tanto, modificamos esto introduciendo una topología en el grupo de Galois.

Sea una extensión de Galois (posible infinito) y sea ​​el grupo de Galois de la extensión. Dejar ${\ Displaystyle E / F}$${\ Displaystyle G = {\ text {Gal}} (E / F)}$

ser el conjunto de los grupos de Galois de todas las extensiones intermedias finitas de Galois. Tenga en cuenta que para todos podemos definir los mapas por . A continuación, definir el Krull Topología de ser más débil topología de tal manera que para todos los mapas son continuas, donde dotamos a cada uno con la topología discreta. Expresado de manera diferente como un límite inverso de grupos topológicos (donde nuevamente cada uno está dotado de la topología discreta). Esto hace un grupo lucrativo (de hecho, cada grupo lucrativo se puede realizar como el grupo Galois de una extensión de Galois, ver por ejemplo). Tenga en cuenta que cuando es finito, la topología de Krull es la topología discreta. ${\ Displaystyle i \ in I}$${\ Displaystyle \ varphi _ {i}: G \ rightarrow G_ {i}}$${\ Displaystyle \ sigma \ mapsto \ sigma _ {| L_ {i}}}$${\ Displaystyle G}$${\ Displaystyle i \ in I}$${\ Displaystyle \ varphi _ {i}: G \ rightarrow G_ {i}}$${\ Displaystyle G_ {i}}$${\ Displaystyle G \ cong \ varprojlim G_ {i}}$${\ Displaystyle G_ {i}}$${\ Displaystyle G}$${\ Displaystyle E / F}$

Ahora que hemos definido una topología en el grupo de Galois, podemos reformular el teorema fundamental de la extensión infinita de Galois.

Deje designar el conjunto de toda la extensión finita campo intermedio de y dejar denotar el conjunto de todos los subgrupos cerrados de estar dotados de la topología de Krull. Entonces existe una biyección entre y dada por el mapa ${\ Displaystyle {\ mathcal {F}}}$${\ Displaystyle E / F}$${\ Displaystyle {\ mathcal {C}}}$${\ Displaystyle G = {\ text {Gal}} (E / F)}$${\ Displaystyle {\ mathcal {F}}}$${\ Displaystyle {\ mathcal {C}}}$

$${\ Displaystyle \ Phi: {\ mathcal {F}} (E / F) \ rightarrow {\ mathcal {C}} (G)}$$

definido por y el mapa ${\ displaystyle L \ mapsto {\ text {Gal}} (E / L)}$

$${\ Displaystyle \ Gamma: {\ mathcal {C}} (G) \ rightarrow {\ mathcal {F}} (E / F)}$$

definido por . Una cosa importante que hay que comprobar es que es un mapa bien definido, es decir, que es un subgrupo cerrado de para todos los intermedios. Para una prueba, ver por ejemplo ${\ Displaystyle N \ mapsto {\ text {Fix}} _ {E} (N): = \ {a \ in E ~ | ~ \ sigma (a) = a {\ text {para todos}} \ sigma \ in NORTE\}}$${\ Displaystyle \ Phi}$${\ Displaystyle \ Phi (L)}$${\ Displaystyle G}$

Referencias

enlaces externos

• Medios relacionados con el teorema fundamental de la teoría de Galois en Wikimedia Commons