Teoría de Galois - Galois theory

El diagrama de celosía de Q se une a las raíces cuadradas positivas de 2 y 3, sus subcampos y los grupos de Galois.

En matemáticas , la teoría de Galois , originalmente introducida por Évariste Galois , proporciona una conexión entre la teoría de campos y la teoría de grupos . Esta conexión, el teorema fundamental de la teoría de Galois , permite reducir ciertos problemas de la teoría de campos a la teoría de grupos, lo que los hace más simples y fáciles de entender.

Galois introdujo el tema para estudiar raíces de polinomios . Esto le permitió caracterizar las ecuaciones polinomiales que se pueden resolver mediante radicales en términos de propiedades del grupo de permutación de sus raíces; una ecuación se puede resolver mediante radicales si sus raíces pueden expresarse mediante una fórmula que incluya solo números enteros , n- ésima raíz y cuatro operaciones aritméticas básicas . Esto generaliza ampliamente el teorema de Abel-Ruffini , que afirma que un polinomio general de grado al menos cinco no puede resolverse mediante radicales.

La teoría de Galois se ha utilizado para resolver problemas clásicos, incluida la demostración de que dos problemas de la antigüedad no se pueden resolver como se indicaron ( duplicar el cubo y trisecar el ángulo ), y caracterizar los polígonos regulares que son construibles (esta caracterización fue dada previamente por Gauss , pero todas las pruebas conocidas de que esta caracterización es completa requieren la teoría de Galois).

El trabajo de Galois fue publicado catorce años después de su muerte por Joseph Liouville . La teoría tardó más en hacerse popular entre los matemáticos y en ser bien entendida.

La teoría de Galois se ha generalizado a las conexiones de Galois y la teoría de Galois de Grothendieck .

Aplicación a problemas clásicos

El nacimiento y desarrollo de la teoría de Galois fue causado por la siguiente pregunta, que fue una de las principales cuestiones matemáticas abiertas hasta principios del siglo XIX:

¿Existe una fórmula para las raíces de una ecuación polinomial de quinto (o superior) grado en términos de los coeficientes del polinomio, utilizando solo las operaciones algebraicas habituales (suma, resta, multiplicación, división) y la aplicación de radicales (raíces cuadradas, raíces cúbicas, etc.)?

El teorema de Abel-Ruffini proporciona un contraejemplo que demuestra que existen ecuaciones polinómicas para las que no puede existir tal fórmula. La teoría de Galois proporciona una respuesta mucho más completa a esta pregunta, al explicar por qué es posible resolver algunas ecuaciones, incluidas todas las de grado cuatro o inferior, de la manera anterior, y por qué no es posible para la mayoría de las ecuaciones de grado cinco. o mas alto. Además, proporciona un medio para determinar si una ecuación particular se puede resolver que sea conceptualmente clara y se exprese fácilmente como un algoritmo .

La teoría de Galois también da una idea clara de las cuestiones relativas a los problemas en la construcción de la brújula y la regla . Da una caracterización elegante de las proporciones de longitudes que se pueden construir con este método. Usando esto, se vuelve relativamente fácil responder a problemas clásicos de geometría como

1. ¿Qué polígonos regulares son construibles ?
2. ¿Por qué no es posible trisecar todos los ángulos con un compás y una regla ?
3. ¿Por qué no es posible duplicar el cubo con el mismo método?

Historia

Prehistoria

La teoría de Galois se originó en el estudio de funciones simétricas : los coeficientes de un polinomio mónico son (hasta el signo) los polinomios simétricos elementales en las raíces. Por ejemplo, ( x - a ) ( x - b ) = x ² - ( a + b ) x + ab , donde 1, a + b y ab son los polinomios elementales de grado 0, 1 y 2 en dos variables.

Esto fue formalizado por primera vez por el matemático francés del siglo XVI François Viète , en las fórmulas de Viète , para el caso de las raíces reales positivas. En opinión del matemático británico del siglo XVIII Charles Hutton , la expresión de los coeficientes de un polinomio en términos de raíces (no solo para raíces positivas) fue entendida por primera vez por el matemático francés del siglo XVII Albert Girard ; Hutton escribe:

... [Girard fue] la primera persona que entendió la doctrina general de la formación de los coeficientes de las potencias a partir de la suma de las raíces y sus productos. Fue el primero en descubrir las reglas para sumar las potencias de las raíces de cualquier ecuación.

En este sentido, el discriminante es una función simétrica en las raíces que refleja las propiedades de las raíces: es cero si y solo si el polinomio tiene una raíz múltiple, y para polinomios cuadráticos y cúbicos es positivo si y solo si todas las raíces son real y distinta, y negativa si y solo si hay un par de raíces conjugadas complejas distintas. Ver Discriminante: Naturaleza de las raíces para más detalles.

El cúbico fue resuelto en parte por primera vez por el matemático italiano del siglo XV al XVI Scipione del Ferro , quien sin embargo no publicó sus resultados; este método, sin embargo, solo resolvió un tipo de ecuación cúbica. Esta solución fue redescubierta de forma independiente en 1535 por Niccolò Fontana Tartaglia , quien la compartió con Gerolamo Cardano y le pidió que no la publicara. Cardano luego extendió esto a muchos otros casos, usando argumentos similares; vea más detalles en el método de Cardano . Tras el descubrimiento de la obra de del Ferro, sintió que el método de Tartaglia ya no era secreto, por lo que publicó su solución en su Ars Magna de 1545 . Su alumno Lodovico Ferrari resolvió el polinomio cuártico; su solución también se incluyó en Ars Magna. En este libro, sin embargo, Cardano no proporcionó una "fórmula general" para la solución de una ecuación cúbica, ya que no tenía números complejos a su disposición, ni la notación algebraica para poder describir una ecuación cúbica general. Con el beneficio de la notación moderna y los números complejos, las fórmulas de este libro funcionan en el caso general, pero Cardano no lo sabía. Fue Rafael Bombelli quien logró entender cómo trabajar con números complejos para resolver todas las formas de ecuación cúbica.

Un paso más fue el artículo de 1770 Réflexions sur la résolution algébrique des équations del matemático franco-italiano Joseph Louis Lagrange , en su método de los solventes de Lagrange , donde analizó la solución de Cardano y Ferrari de cúbicos y cuárticos considerándolos en términos de permutaciones de las raíces, que produjeron un polinomio auxiliar de menor grado, proporcionando una comprensión unificada de las soluciones y sentando las bases para la teoría de grupos y la teoría de Galois. Sin embargo, lo más importante es que no consideró la composición de las permutaciones. El método de Lagrange no se extendió a ecuaciones quínticas o superiores, porque el resolutivo tenía mayor grado.

Paolo Ruffini en 1799 casi demostró que la quíntica no tenía soluciones generales por parte de los radicales , cuya idea clave era utilizar grupos de permutación , no solo una permutación única. Su solución contenía una brecha, que Cauchy consideró menor, aunque no se corrigió hasta el trabajo del matemático noruego Niels Henrik Abel , quien publicó una demostración en 1824, estableciendo así el teorema de Abel-Ruffini .

Si bien Ruffini y Abel establecieron que la quintica general no se podía resolver, se pueden resolver algunas quínticas particulares , como x ⁵ - 1 = 0 , y el criterio preciso por el cual una quintica dada o un polinomio superior podría determinarse como soluble o no. Fue dado por Évariste Galois , quien demostró que si un polinomio era o no soluble era equivalente a si el grupo de permutación de sus raíces - en términos modernos, su grupo de Galois - tenía una cierta estructura - en términos modernos, si o no era un grupo solucionable . Este grupo siempre se pudo resolver para polinomios de grado cuatro o menos, pero no siempre lo fue para polinomios de grado cinco y mayores, lo que explica por qué no existe una solución general en grados superiores.

Los escritos de Galois

Un retrato de Évariste Galois de unos 15 años

En 1830 Galois (a la edad de 18 años) presentó a la Academia de Ciencias de París una memoria sobre su teoría de la solubilidad por radicales; El artículo de Galois fue finalmente rechazado en 1831 por ser demasiado esquemático y por dar una condición en términos de las raíces de la ecuación en lugar de sus coeficientes. Galois luego murió en un duelo en 1832, y su artículo, " Mémoire sur les conditions de résolubilité des équations par radicaux ", permaneció inédito hasta 1846 cuando fue publicado por Joseph Liouville acompañado de algunas de sus propias explicaciones. Antes de esta publicación, Liouville anunció el resultado de Galois a la Academia en un discurso que pronunció el 4 de julio de 1843. Según Allan Clark, la caracterización de Galois "reemplaza dramáticamente el trabajo de Abel y Ruffini".

Secuelas

La teoría de Galois fue notoriamente difícil de entender para sus contemporáneos, especialmente en el nivel en que pudieron expandirla. Por ejemplo, en su comentario de 1846, Liouville perdió por completo el núcleo de la teoría de grupos del método de Galois. Joseph Alfred Serret, que asistió a algunas de las charlas de Liouville, incluyó la teoría de Galois en su 1866 (tercera edición) de su libro de texto Cours d'algèbre supérieure . La alumna de Serret, Camille Jordan , tuvo una comprensión aún mejor reflejada en su libro de 1870 Traité des substitutions et des équations algébriques . Fuera de Francia, la teoría de Galois permaneció más oscura durante un período más largo. En Gran Bretaña, Cayley no logró captar su profundidad y los populares libros de texto de álgebra británicos ni siquiera mencionaron la teoría de Galois hasta mucho después del cambio de siglo. En Alemania, los escritos de Kronecker se centraron más en el resultado de Abel. Dedekind escribió poco sobre la teoría de Galois, pero dio una conferencia sobre ella en Gotinga en 1858, mostrando una muy buena comprensión. Los libros de Eugen Netto de la década de 1880, basados ​​en el Traité de Jordan , hicieron que la teoría de Galois fuera accesible a una audiencia alemana y estadounidense más amplia, al igual que el libro de texto de álgebra de 1895 de Heinrich Martin Weber .

Enfoque de grupo de permutación

Dado un polinomio, puede ser que algunas de las raíces estén conectadas por varias ecuaciones algebraicas . Por ejemplo, puede ser que para dos de las raíces, digamos A y B , A ² + 5 B ³ = 7 . La idea central de la teoría de Galois es considerar las permutaciones (o reordenamientos) de las raíces de modo que cualquier ecuación algebraica satisfecha por las raíces todavía se satisfaga después de que las raíces hayan sido permutadas. Originalmente, la teoría se había desarrollado para ecuaciones algebraicas cuyos coeficientes son números racionales . Se extiende naturalmente a ecuaciones con coeficientes en cualquier campo , pero esto no se considerará en los ejemplos simples a continuación.

Estas permutaciones juntas forman un grupo de permutación , también llamado grupo de Galois del polinomio, que se describe explícitamente en los siguientes ejemplos.

Ecuación cuadrática

Considere la ecuación cuadrática

${\ displaystyle x ^ {2} -4x + 1 = 0.}$

Al usar la fórmula cuadrática , encontramos que las dos raíces son

${\ Displaystyle {\ begin {alineado} A & = 2 + {\ sqrt {3}}, \\ B & = 2 - {\ sqrt {3}}. \ end {alineado}}}$

Ejemplos de ecuaciones algebraicas satisfechas por A y B incluyen

${\ Displaystyle A + B = 4,}$

y

${\ Displaystyle AB = 1.}$

Si intercambiamos A y B en cualquiera de las dos últimas ecuaciones obtenemos otro enunciado verdadero. Por ejemplo, la ecuación A + B = 4 se convierte en B + A = 4 . En términos más generales, es cierto que esto es válido para todas las posibles relaciones algebraicas entre A y B , de manera que todos los coeficientes son racionales ; es decir, en cualquier relación de este tipo, intercambiar A y B produce otra relación verdadera. Esto resulta de la teoría de polinomios simétricos , que, en este caso, pueden ser reemplazados por manipulaciones de fórmulas que involucran el teorema del binomio .

Uno podría objetar que A y B están relacionados por la ecuación algebraica A - B - 2 √ 3 = 0 , que no permanece verdadera cuando A y B se intercambian. Sin embargo, esta relación no se considera aquí, porque tiene el coeficiente −2 √ 3 que no es racional .

Llegamos a la conclusión de que el grupo de Galois del polinomio x ² - 4 x + 1 se compone de dos permutaciones: la identidad de permutación que deja A y B sin tocar, y la transposición de permutación que intercambia A y B . Es un grupo cíclico de orden dos, y por lo tanto isomorfo a Z / 2 Z .

Una discusión similar se aplica a cualquier polinomio cuadrático ax ² + bx + c , donde a , b y c son números racionales.

• Si el polinomio tiene raíces racionales, por ejemplo x ² - 4 x + 4 = ( x - 2) ² , o x ² - 3 x + 2 = ( x - 2) ( x - 1) , entonces el grupo de Galois es trivial ; es decir, contiene solo la permutación de identidad. En este ejemplo, si A = 2 y B = 1, entonces A - B = 1 ya no es cierto cuando A y B se intercambian.
• Si tiene dos raíces irracionales , por ejemplo x ² - 2 , entonces el grupo de Galois contiene dos permutaciones, como en el ejemplo anterior.

Ecuación cuartica

Considere el polinomio

${\ displaystyle x ^ {4} -10x ^ {2} +1,}$

que también se puede escribir como

${\ Displaystyle \ left (x ^ {2} -5 \ right) ^ {2} -24.}$

Deseamos describir el grupo de Galois de este polinomio, nuevamente sobre el campo de los números racionales . El polinomio tiene cuatro raíces:

${\ Displaystyle {\ begin {alineado} A & = {\ sqrt {2}} + {\ sqrt {3}}, \\ B & = {\ sqrt {2}} - {\ sqrt {3}}, \\ C & = - {\ sqrt {2}} + {\ sqrt {3}}, \\ D & = - {\ sqrt {2}} - {\ sqrt {3}}. \ end {alineado}}}$

Hay 24 formas posibles de permutar estas cuatro raíces, pero no todas estas permutaciones son miembros del grupo de Galois. Los miembros del grupo de Galois deben preservar cualquier ecuación algebraica con coeficientes racionales que involucran A , B , C y D .

Entre estas ecuaciones, tenemos:

${\ displaystyle {\ begin {alineado} AB & = - 1 \\ AC & = 1 \\ A + D & = 0 \ end {alineado}}}$

De ello se deduce que, si φ es una permutación que pertenece al grupo de Galois, debemos tener:

${\ Displaystyle {\ begin {alineado} \ varphi (B) & = {\ frac {-1} {\ varphi (A)}}, \\\ varphi (C) & = {\ frac {1} {\ varphi (A)}}, \\\ varphi (D) & = - \ varphi (A). \ End {alineado}}}$

Esto implica que la permutación está bien definida por la imagen de A , y que el grupo de Galois tiene 4 elementos, que son:

( A , B , C , D ) → ( A , B , C , D )

( A , B , C , D ) → ( B , A , D , C )

( A , B , C , D ) → ( C , D , A , B )

( A , B , C , D ) → ( D , C , B , A )

Esto implica que el grupo de Galois es isomorfo al grupo de cuatro de Klein .

Enfoque moderno por teoría de campo

En el enfoque moderno, se empieza con una extensión de cuerpos L / K (leen " L sobre K "), y examina el grupo de automorfismos de L que fijan K . Consulte el artículo sobre los grupos de Galois para obtener más explicaciones y ejemplos.

La conexión entre los dos enfoques es la siguiente. Los coeficientes del polinomio en cuestión deben ser elegidos entre el campo base de K . El campo superior L debe ser el campo obtenido al unir las raíces del polinomio en cuestión al campo base. Cualquier permutación de las raíces que respete las ecuaciones algebraicas descritas anteriormente da lugar a un automorfismo de L / K y viceversa.

En el primer ejemplo anterior, estábamos estudiando la extensión Q ( √ 3 ) / Q , donde Q es el campo de los números racionales y Q ( √ 3 ) es el campo obtenido de Q al unir √ 3 . En el segundo ejemplo, estábamos estudiando la extensión Q ( A , B , C , D ) / Q .

Hay varias ventajas del enfoque moderno sobre el enfoque de grupo de permutación.

• Permite una declaración mucho más simple del teorema fundamental de la teoría de Galois .
• El uso de campos base distintos de Q es crucial en muchas áreas de las matemáticas. Por ejemplo, en la teoría algebraica de números , a menudo se aplica la teoría de Galois utilizando campos numéricos , campos finitos o campos locales como campo base.
• Permite a uno estudiar más fácilmente extensiones infinitas. De nuevo, esto es importante en la teoría de números algebraica, donde por ejemplo, uno a menudo discute el grupo de Galois absoluto de Q , definido para ser el grupo de Galois de K / Q , donde K es una clausura algebraica de Q .
• Permite considerar extensiones inseparables . Este problema no surge en el marco clásico, ya que siempre se asumió implícitamente que la aritmética tenía lugar en la característica cero, pero la característica distinta de cero surge con frecuencia en la teoría de números y en la geometría algebraica .
• Elimina la dependencia bastante artificial de perseguir raíces de polinomios. Es decir, diferentes polinomios pueden producir los mismos campos de extensión y el enfoque moderno reconoce la conexión entre estos polinomios.

Grupos solubles y solución por radicales

La noción de grupo soluble en la teoría de grupos permite determinar si un polinomio se puede resolver en radicales, dependiendo de si su grupo de Galois tiene la propiedad de solubilidad. En esencia, cada extensión de campo L / K corresponde a un grupo de factores en una serie de composición del grupo de Galois. Si un grupo de factores en la serie de composición es cíclico de orden n , y si en la extensión de campo correspondiente L / K el campo K ya contiene una raíz primitiva n -ésima de la unidad , entonces es una extensión radical y los elementos de L pueden entonces ser expresado usando el n º raíz de algún elemento de K .

Si todos los grupos de factores en su serie de composición son cíclicos, el grupo de Galois se llama solucionable , y todos los elementos del campo correspondiente se pueden encontrar extrayendo raíces, productos y sumas de elementos del campo base (generalmente Q ) repetidamente . .

Uno de los grandes triunfos de la Teoría de Galois fue la demostración de que por cada n > 4 , existen polinomios de grado n que no se pueden resolver por radicales (esto fue probado de forma independiente, utilizando un método similar, por Niels Henrik Abel unos años antes, y es el teorema de Abel-Ruffini ), y una forma sistemática de probar si un polinomio específico se puede resolver mediante radicales. El teorema de Abel-Ruffini resulta del hecho de que para n > 4 el grupo simétrico S _n contiene un subgrupo normal simple , no cíclico , a saber, el grupo alterno A _n .

Un ejemplo quíntico no resoluble

Para el polinomio f ( x ) = x ⁵ - x - 1 , la única raíz real x = 1.1673 ... es algebraica, pero no se puede expresar en términos de radicales. Las otras cuatro raíces son números complejos .

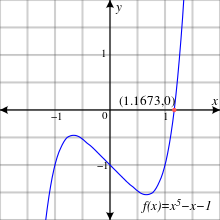
Van der Waerden cita el polinomio f ( x ) = x ⁵ - x - 1 . Según el teorema de la raíz racional, esto no tiene ceros racionales. Tampoco tiene factores lineales módulo 2 o 3.

El grupo de Galois de f ( x ) módulo 2 es cíclico de orden 6, porque f ( x ) módulo 2 se factoriza en polinomios de órdenes 2 y 3, ( x ² + x + 1) ( x ³ + x ² + 1) .

f ( x ) módulo 3 no tiene factor lineal o cuadrático y, por tanto, es irreducible. Por tanto, su grupo de Galois módulo 3 contiene un elemento de orden 5.

Se sabe que un grupo de Galois módulo a primo es isomorfo a un subgrupo del grupo de Galois sobre los racionales. Un grupo de permutación en 5 objetos con elementos de órdenes 6 y 5 debe ser el grupo simétrico S ₅ , que es por lo tanto el grupo de Galois de f ( x ) . Este es uno de los ejemplos más simples de un polinomio quíntico no soluble. Según Serge Lang , a Emil Artin le gustaba este ejemplo.

Problema de Galois inverso

El problema de Galois inverso es encontrar una extensión de campo con un grupo de Galois dado.

Mientras uno no especifique también el campo de tierra , el problema no es muy difícil y todos los grupos finitos ocurren como grupos de Galois. Para mostrar esto, se puede proceder de la siguiente manera. Elija un campo K y un grupo finito G . El teorema de Cayley dice que G es (hasta isomorfismo) un subgrupo del grupo simétrico S en los elementos de G . Elija indeterminados { x _α } , uno para cada elemento α de G , y colóquelos junto a K para obtener el campo F = K ({ x _α }) . Dentro de F está el campo L de funciones racionales simétricas en { x _α } . El grupo de Galois de F / L es S , por un resultado básico de Emil Artin. G actúa sobre F por la restricción de acción de S . Si el campo fijo de esta acción es M , entonces, por el teorema fundamental de la teoría de Galois , el grupo de Galois de F / M es G .

Por otro lado, es un problema abierto si cada grupo finito es el grupo de Galois de una extensión de campo del campo Q de los números racionales. Igor Shafarevich demostró que todo grupo finito solucionable es el grupo de Galois de alguna extensión de Q . Varias personas han resuelto el problema inverso de Galois para grupos simples no abelianos seleccionados . Se ha demostrado la existencia de soluciones para todos excepto posiblemente uno ( grupo de Mathieu M ₂₃ ) de los 26 grupos simples esporádicos. Incluso hay un polinomio con coeficientes integrales cuyo grupo de Galois es el grupo Monster .

Extensiones inseparables

En la forma mencionada anteriormente, incluyendo en particular el teorema fundamental de la teoría de Galois , la teoría solo considera extensiones de Galois, que son en particular separables. Las extensiones de campo generales se pueden dividir en una extensión de campo separable, seguida de una extensión de campo puramente inseparable . Para una extensión puramente inseparable F / K , hay una teoría de Galois donde el grupo de Galois se sustituye por el espacio vectorial de las derivaciones , , es decir, K - endomorfismos lineales de F que satisfacen la regla de Leibniz. En esta correspondencia, se asigna un campo E intermedio . A la inversa, se asigna un subespacio que satisface las condiciones adicionales apropiadas . Bajo el supuesto , Jacobson (1944) mostró que esto establece una correspondencia uno a uno. La condición impuesta por Jacobson ha sido eliminada por Brantner & Waldron (2020) , al dar una correspondencia utilizando nociones de geometría algebraica derivada . ${\ Displaystyle Der_ {K} (F, F)}$${\ Displaystyle Der_ {E} (F, F) \ subset Der_ {K} (F, F)}$ ${\ Displaystyle V \ subconjunto Der_ {K} (F, F)}$${\ Displaystyle \ {x \ en F, f (x) = 0 \ \ forall f \ in V \}}$${\ Displaystyle F ^ {p} \ subconjunto K}$

Ver también

• Grupo Galois para más ejemplos
• Teorema fundamental de la teoría de Galois
• Teoría diferencial de Galois para una teoría de ecuaciones diferenciales de Galois
• Teoría de Galois de Grothendieck para una vasta generalización de la teoría de Galois
• Teoría topológica de Galois

Notas

Referencias

• Artin, Emil (1998) [1944]. Teoría de Galois . Dover. ISBN 0-486-62342-4.
• Bewersdorff, Jörg (2006). Teoría de Galois para principiantes: una perspectiva histórica . La biblioteca matemática estudiantil. 35 . Sociedad Matemática Estadounidense. doi : 10.1090 / stml / 035 . ISBN 0-8218-3817-2.
• Brantner, Lukas; Waldron, Joe (2020), Teoría de Galois puramente inseparable I: El teorema fundamental , arXiv : 2010.15707
• Cardano, Gerolamo (1545). Artis Magnæ (PDF) (en latín).
• Edwards, Harold M. (1984). Teoría de Galois . Springer-Verlag. ISBN 0-387-90980-X. (El artículo original de Galois, con amplios antecedentes y comentarios).
• Funkhouser, H. Gray (1930). "Una breve descripción de la historia de las funciones simétricas de raíces de ecuaciones". American Mathematical Monthly . 37 (7): 357–365. doi : 10.2307 / 2299273 . JSTOR  2299273 .
• "Teoría de Galois" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Jacobson, Nathan (1944), "Teoría de Galois de campos puramente inseparables del exponente uno", Amer. J. Math. , 66 : 645–648, doi : 10.2307 / 2371772 , JSTOR  2371772
• Jacobson, Nathan (1985). Álgebra básica I (2ª ed.). WH Freeman. ISBN 0-7167-1480-9. (El capítulo 4 ofrece una introducción al enfoque de la teoría de campo de la teoría de Galois).
• Janelidze, G .; Borceux, Francis (2001). Teorías de Galois . Prensa de la Universidad de Cambridge . ISBN 978-0-521-80309-0.(Este libro presenta al lector la teoría de Galois de Grothendieck y algunas generalizaciones que conducen a los grupoides de Galois ).
• Lang, Serge (1994). Teoría algebraica de números . Berlín, Nueva York: Springer-Verlag . ISBN 978-0-387-94225-4.
• Postnikov, MM (2004). Fundamentos de la teoría de Galois . Publicaciones de Dover. ISBN 0-486-43518-0.
• Rotman, Joseph (1998). Teoría de Galois (2ª ed.). Saltador. ISBN 0-387-98541-7.
• Völklein, Helmut (1996). Grupos como grupos de Galois: una introducción . Prensa de la Universidad de Cambridge . ISBN 978-0-521-56280-5.
• van der Waerden, Bartel Leendert (1931). Moderne Algebra (en alemán). Berlín: Springer.. Traducción al inglés (de la 2ª edición revisada): Álgebra moderna . Nueva York: Frederick Ungar. 1949. (Más tarde reeditado en inglés por Springer bajo el título "Álgebra").

enlaces externos

• La definición del diccionario de la teoría de Galois en Wikcionario
• Medios relacionados con la teoría de Galois en Wikimedia Commons