Proceso gaussiano - Gaussian process

En teoría de probabilidad y estadística , un proceso gaussiano es un proceso estocástico (una colección de variables aleatorias indexadas por tiempo o espacio), de modo que cada colección finita de esas variables aleatorias tiene una distribución normal multivariante , es decir, cada combinación lineal finita de ellas es normalmente repartido. La distribución de un proceso gaussiano es la distribución conjunta de todas esas (infinitas) variables aleatorias y, como tal, es una distribución sobre funciones con un dominio continuo, por ejemplo, tiempo o espacio.

El concepto de procesos gaussianos lleva el nombre de Carl Friedrich Gauss porque se basa en la noción de distribución gaussiana ( distribución normal ). Los procesos gaussianos pueden verse como una generalización de dimensiones infinitas de distribuciones normales multivariadas.

Los procesos gaussianos son útiles en el modelado estadístico , beneficiándose de las propiedades heredadas de la distribución normal. Por ejemplo, si un proceso aleatorio se modela como un proceso gaussiano, las distribuciones de varias cantidades derivadas se pueden obtener explícitamente. Tales cantidades incluyen el valor promedio del proceso en un rango de tiempos y el error al estimar el promedio usando valores de muestra en un pequeño conjunto de tiempos. Si bien los modelos exactos a menudo escalan mal a medida que aumenta la cantidad de datos, se han desarrollado múltiples métodos de aproximación que a menudo conservan una buena precisión al tiempo que reducen drásticamente el tiempo de cálculo.

Definición

Un proceso estocástico continuo en el tiempo es gaussiano si y solo si para cada conjunto finito de índices en el conjunto de índices${\ Displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$ ${\ Displaystyle t_ {1}, \ ldots, t_ {k}}$${\ Displaystyle T}$

${\ Displaystyle \ mathbf {X} _ {t_ {1}, \ ldots, t_ {k}} = (X_ {t_ {1}}, \ ldots, X_ {t_ {k}})}$

es una variable aleatoria gaussiana multivariante . Eso es lo mismo que decir que cada combinación lineal de tiene una distribución normal univariante (o gaussiana). ${\ Displaystyle (X_ {t_ {1}}, \ ldots, X_ {t_ {k}})}$

Utilizando funciones características de variables aleatorias, la propiedad gaussiana se puede formular de la siguiente manera: es gaussiana si y solo si, para cada conjunto finito de índices , hay valores reales , de modo que la siguiente igualdad se cumple para todos${\ Displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$${\ Displaystyle t_ {1}, \ ldots, t_ {k}}$${\ Displaystyle \ sigma _ {\ ell j}}$${\ Displaystyle \ mu _ {\ ell}}$${\ Displaystyle \ sigma _ {jj}> 0}$${\ Displaystyle s_ {1}, s_ {2}, \ ldots, s_ {k} \ in \ mathbb {R}}$

${\ Displaystyle \ operatorname {E} \ left (\ exp \ left (i \ \ sum _ {\ ell = 1} ^ {k} s _ {\ ell} \ \ mathbf {X} _ {t _ {\ ell}} \ right) \ right) = \ exp \ left (- {\ frac {1} {2}} \, \ sum _ {\ ell, j} \ sigma _ {\ ell j} s _ {\ ell} s_ {j } + i \ sum _ {\ ell} \ mu _ {\ ell} s _ {\ ell} \ right)}$.

donde denota la unidad imaginaria tal que . ${\ Displaystyle i}$${\ Displaystyle i ^ {2} = - 1}$

Se puede demostrar que los números y son las covarianzas y medias de las variables en el proceso. ${\ Displaystyle \ sigma _ {\ ell j}}$${\ Displaystyle \ mu _ {\ ell}}$

Diferencia

La varianza de un proceso gaussiano es finita en cualquier momento , formalmente ${\ Displaystyle t}$

${\ Displaystyle \ operatorname {var} [X (t)] = \ operatorname {E} [| X (t) - \ operatorname {E} [X (t)] | ^ {2}] <\ infty \ quad { \ text {para todos}} t \ in T}$.

Estacionariedad

Para los procesos estocásticos generales, la estacionariedad en sentido estricto implica una estacionariedad en sentido amplio, pero no todos los procesos estocásticos estacionarios en sentido amplio son estacionarios en sentido estricto. Sin embargo, para un proceso estocástico gaussiano, los dos conceptos son equivalentes.

Un proceso estocástico gaussiano es estacionario en sentido estricto si, y solo si, es estacionario en sentido amplio.

Ejemplo

Hay una representación explícita de los procesos gaussianos estacionarios. Un ejemplo simple de esta representación es

${\ Displaystyle X_ {t} = \ cos (en) \ xi _ {1} + \ sin (en) \ xi _ {2}}$

donde y son variables aleatorias independientes con la distribución normal estándar . ${\ Displaystyle \ xi _ {1}}$${\ Displaystyle \ xi _ {2}}$

Funciones de covarianza

Un hecho clave de los procesos gaussianos es que pueden definirse completamente mediante sus estadísticas de segundo orden. Por lo tanto, si se supone que un proceso gaussiano tiene una media de cero, definir la función de covarianza define completamente el comportamiento del proceso. Es importante destacar que la definición no negativa de esta función permite su descomposición espectral utilizando la expansión Karhunen-Loève . Los aspectos básicos que se pueden definir a través de la función de covarianza son la estacionariedad , isotropía , suavidad y periodicidad del proceso .

La estacionariedad se refiere al comportamiento del proceso con respecto a la separación de dos puntos cualesquiera y . Si el proceso es estacionario, depende de su separación, mientras que si no es estacionario, depende de la posición real de los puntos y . Por ejemplo, el caso especial de un proceso de Ornstein-Uhlenbeck , un proceso de movimiento browniano , es estacionario. ${\ Displaystyle x}$${\ Displaystyle x '}$${\ Displaystyle x-x '}$${\ Displaystyle x}$${\ Displaystyle x '}$

Si el proceso depende solo de la distancia euclidiana (no la dirección) entre y , entonces el proceso se considera isotrópico. Un proceso que es simultáneamente estacionario e isotrópico se considera homogéneo ; en la práctica, estas propiedades reflejan las diferencias (o más bien la falta de ellas) en el comportamiento del proceso dada la ubicación del observador. ${\ Displaystyle | x-x '|}$${\ Displaystyle x}$${\ Displaystyle x '}$

En última instancia, los procesos gaussianos se traducen en la adopción de priores en funciones y la suavidad de estos priores puede ser inducida por la función de covarianza. Si esperamos que para "cerca-por" puntos de entrada y sus puntos de salida correspondientes y para ser "cerca-by" también, entonces la suposición de continuidad está presente. Si deseamos permitir un desplazamiento significativo, entonces podríamos elegir una función de covarianza más aproximada. Ejemplos extremos del comportamiento son la función de covarianza de Ornstein-Uhlenbeck y el cuadrado exponencial donde el primero nunca es diferenciable y el segundo infinitamente diferenciable. ${\ Displaystyle x}$${\ Displaystyle x '}$${\ Displaystyle y}$${\ Displaystyle y '}$

La periodicidad se refiere a inducir patrones periódicos dentro del comportamiento del proceso. Formalmente, esto se logra mapeando la entrada a un vector bidimensional . ${\ Displaystyle x}$${\ Displaystyle u (x) = \ left (\ cos (x), \ sin (x) \ right)}$

Funciones de covarianza habituales

El efecto de elegir diferentes núcleos en la distribución de funciones previa del proceso gaussiano. La izquierda es un núcleo exponencial al cuadrado. El medio es browniano. La derecha es cuadrática.

Hay una serie de funciones de covarianza comunes:

• Constante: ${\ Displaystyle K _ {\ operatorname {C}} (x, x ') = C}$
• Lineal: ${\ Displaystyle K _ {\ operatorname {L}} (x, x ') = x ^ {T} x'}$
• ruido gaussiano blanco: ${\ Displaystyle K _ {\ operatorname {GN}} (x, x ') = \ sigma ^ {2} \ delta _ {x, x'}}$
• Exponencial al cuadrado: ${\ Displaystyle K _ {\ operatorname {SE}} (x, x ') = \ exp {\ Big (} - {\ frac {| d | ^ {2}} {2 \ ell ^ {2}}} {\ Grande )}}$
• Ornstein – Uhlenbeck: ${\ Displaystyle K _ {\ operatorname {OU}} (x, x ') = \ exp \ left (- {\ frac {| d |} {\ ell}} \ right)}$
• Materia: ${\ Displaystyle K _ {\ operatorname {Matern}} (x, x ') = {\ frac {2 ^ {1- \ nu}} {\ Gamma (\ nu)}} {\ Big (} {\ frac {{ \ sqrt {2 \ nu}} | d |} {\ ell}} {\ Big)} ^ {\ nu} K _ {\ nu} {\ Big (} {\ frac {{\ sqrt {2 \ nu}} | d |} {\ ell}} {\ Big)}}$
• Periódico: ${\ Displaystyle K _ {\ operatorname {P}} (x, x ') = \ exp \ left (- {\ frac {2 \ sin ^ {2} \ left ({\ frac {d} {2}} \ right )} {\ ell ^ {2}}} \ right)}$
• Cuadrática racional: ${\ Displaystyle K _ {\ operatorname {RQ}} (x, x ') = (1+ | d | ^ {2}) ^ {- \ alpha}, \ quad \ alpha \ geq 0}$

Aquí . El parámetro es la escala de longitud característica del proceso (prácticamente, "qué tan cerca" deben estar dos puntos y deben influirse entre sí de manera significativa), es el delta de Kronecker y la desviación estándar de las fluctuaciones del ruido. Además, es la función de orden de Bessel modificada y es la función gamma evaluada en . Es importante destacar que una función de covarianza complicada se puede definir como una combinación lineal de otras funciones de covarianza más simples para incorporar diferentes conocimientos sobre el conjunto de datos en cuestión. ${\ Displaystyle d = x-x '}$${\ Displaystyle \ ell}$${\ Displaystyle x}$${\ Displaystyle x '}$${\ Displaystyle \ delta}$${\ Displaystyle \ sigma}$${\ Displaystyle K _ {\ nu}}$${\ Displaystyle \ nu}$${\ Displaystyle \ Gamma (\ nu)}$${\ Displaystyle \ nu}$

Claramente, los resultados inferenciales dependen de los valores de los hiperparámetros (por ejemplo, y ) que definen el comportamiento del modelo. Una opción popular para es proporcionar estimaciones máximas a posteriori (MAP) de la misma con algunas elegidas a priori. Si el a priori es casi uniforme, esto equivale a maximizar la probabilidad marginal del proceso; la marginación se realiza sobre los valores de proceso observados . Este enfoque también se conoce como máxima verosimilitud II , maximización de evidencia o Bayes empírico . ${\ Displaystyle \ theta}$${\ Displaystyle \ ell}$${\ Displaystyle \ sigma}$${\ Displaystyle \ theta}$${\ Displaystyle y}$

Continuidad

Para un proceso gaussiano, la continuidad en la probabilidad es equivalente a la continuidad del cuadrado medio , y la continuidad con la probabilidad uno es equivalente a la continuidad de la muestra . Esto último implica, pero no implica, continuidad en la probabilidad. La continuidad en la probabilidad se mantiene si y solo si la media y la autocovarianza son funciones continuas. Por el contrario, la continuidad de la muestra fue un desafío incluso para los procesos gaussianos estacionarios (como probablemente señaló primero Andrey Kolmogorov ), y más desafiante para los procesos más generales. Como es habitual, por un proceso continuo de muestra se entiende un proceso que admite una modificación continua de muestra .

Caja estacionaria

Para un proceso gaussiano estacionario, algunas condiciones en su espectro son suficientes para la continuidad de la muestra, pero no son necesarias. Una condición necesaria y suficiente, a veces llamada teorema de Dudley-Fernique, involucra la función definida por ${\ Displaystyle X = (X_ {t}) _ {t \ in \ mathbb {R}},}$${\ Displaystyle \ sigma}$

${\ Displaystyle \ sigma (h) = {\ sqrt {\ mathbb {E} {\ big (} X (t + h) -X (t) {\ big)} ^ {2}}}}$

(el lado derecho no depende de debido a la estacionariedad). La continuidad de en probabilidad es equivalente a la continuidad de en Cuando la convergencia de a (as ) es demasiado lenta, la continuidad de la muestra de puede fallar. La convergencia de las siguientes integrales importa: ${\ Displaystyle t}$${\ Displaystyle X}$${\ Displaystyle \ sigma}$${\ Displaystyle 0.}$${\ Displaystyle \ sigma (h)}$${\ Displaystyle 0}$${\ Displaystyle h \ to 0}$${\ Displaystyle X}$

${\ Displaystyle I (\ sigma) = \ int _ {0} ^ {1} {\ frac {\ sigma (h)} {h {\ sqrt {\ log (1 / h)}}}} \, dh = \ int _ {0} ^ {\ infty} 2 \ sigma (\ mathbb {e} ^ {- x ^ {2}}) \, dx,}$

estas dos integrales son iguales de acuerdo con la integración por sustitución. El primer integrando no necesita estar acotado ya que, por lo tanto, la integral puede converger ( ) o divergir ( ). Tomando, por ejemplo, para grande , es decir, para pequeño, se obtiene cuándo y cuándo. En estos dos casos, la función aumenta, pero generalmente no es así. Además, la condición ${\ Displaystyle h = \ mathbb {e} ^ {- x ^ {2}},}$ ${\ Displaystyle \ textstyle x = {\ sqrt {\ log (1 / h)}}.}$${\ Displaystyle h \ to 0+,}$${\ Displaystyle I (\ sigma) <\ infty}$${\ Displaystyle I (\ sigma) = \ infty}$${\ Displaystyle \ sigma (\ mathbb {e} ^ {- x ^ {2}}) = {\ tfrac {1} {x ^ {a}}}}$${\ Displaystyle x,}$${\ Displaystyle \ sigma (h) = (\ log (1 / h)) ^ {- a / 2}}$${\ Displaystyle h,}$${\ Displaystyle I (\ sigma) <\ infty}$${\ Displaystyle a> 1,}$${\ Displaystyle I (\ sigma) = \ infty}$${\ Displaystyle 0 <a \ leq 1.}$${\ Displaystyle \ sigma}$${\ Displaystyle [0, \ infty),}$

${\ Displaystyle (*)}$   existe tal que es monótono en${\ Displaystyle \ varepsilon> 0}$${\ Displaystyle \ sigma}$${\ displaystyle [0, \ varepsilon]}$

no se sigue de la continuidad de y las relaciones evidentes (para todos ) y${\ Displaystyle \ sigma}$${\ Displaystyle \ sigma (h) \ geq 0}$${\ Displaystyle h}$${\ Displaystyle \ sigma (0) = 0.}$

Teorema 1.   Sea continuo y satisfaga Entonces la condición es necesaria y suficiente para la continuidad muestral de${\ Displaystyle \ sigma}$${\ Displaystyle (*).}$${\ Displaystyle I (\ sigma) <\ infty}$${\ Displaystyle X.}$

Algo de historia. La suficiencia fue anunciada por Xavier Fernique en 1964, pero la primera prueba fue publicada por Richard M. Dudley en 1967. La necesidad fue demostrada por Michael B. Marcus y Lawrence Shepp en 1970.

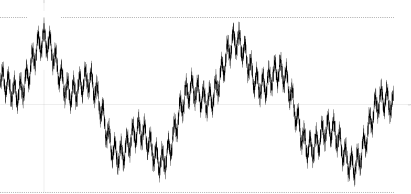
Existen muestras de procesos continuos que violan la condición Un ejemplo encontrado por Marcus y Shepp es una serie lacunar aleatoria de Fourier${\ Displaystyle X}$${\ Displaystyle I (\ sigma) = \ infty;}$${\ Displaystyle (*).}$

${\ Displaystyle X_ {t} = \ sum _ {n = 1} ^ {\ infty} c_ {n} (\ xi _ {n} \ cos \ lambda _ {n} t + \ eta _ {n} \ sin \ lambda _ {n} t),}$

donde son variables aleatorias independientes con distribución normal estándar ; las frecuencias son una secuencia de rápido crecimiento; y los coeficientes satisfacen La última relación implica de dónde es casi seguro, lo que asegura la convergencia uniforme de la serie de Fourier casi seguramente, y la continuidad muestral de${\ Displaystyle \ xi _ {1}, \ eta _ {1}, \ xi _ {2}, \ eta _ {2}, \ dots}$${\ Displaystyle 0 <\ lambda _ {1} <\ lambda _ {2} <\ dots}$${\ Displaystyle c_ {n}> 0}$${\ Displaystyle \ textstyle \ sum _ {n} c_ {n} <\ infty.}$${\ Displaystyle \ textstyle \ mathbb {E} \ sum _ {n} c_ {n} (| \ xi _ {n} | + | \ eta _ {n} |) = \ sum _ {n} c_ {n} \ mathbb {E} (| \ xi _ {n} | + | \ eta _ {n} |) = {\ text {const}} \ cdot \ sum _ {n} c_ {n} <\ infty,}$${\ Displaystyle \ sum _ {n} c_ {n} (| \ xi _ {n} | + | \ eta _ {n} |) <\ infty}$${\ Displaystyle X.}$

Autocorrelación de una serie lacunar aleatoria de Fourier

Su función de autocovariación

${\ Displaystyle \ mathbb {E} X_ {t} X_ {t + h} = \ sum _ {n = 1} ^ {\ infty} c_ {n} ^ {2} \ cos \ lambda _ {n} h}$

no es monótono en ninguna parte (ver la imagen), así como la función correspondiente ${\ Displaystyle \ sigma,}$

${\ Displaystyle \ sigma (h) = {\ sqrt {2 \ mathbb {E} X_ {t} X_ {t} -2 \ mathbb {E} X_ {t} X_ {t + h}}} = 2 {\ sqrt {\ sum _ {n = 1} ^ {\ infty} c_ {n} ^ {2} \ sin ^ {2} {\ frac {\ lambda _ {n} h} {2}}}}.}$

El movimiento browniano como integral de los procesos gaussianos

Un proceso de Wiener (también conocido como movimiento browniano) es la integral de un proceso gaussiano generalizado de ruido blanco . No es estacionario , pero tiene incrementos estacionarios.

El proceso de Ornstein-Uhlenbeck es un proceso gaussiano estacionario .

El puente browniano es (como el proceso de Ornstein-Uhlenbeck) un ejemplo de un proceso gaussiano cuyos incrementos no son independientes .

El movimiento browniano fraccional es un proceso gaussiano cuya función de covarianza es una generalización de la del proceso de Wiener.

Ley cero-uno de Driscoll

La ley cero-uno de Driscoll es un resultado que caracteriza las funciones de muestra generadas por un proceso gaussiano.

Sea un proceso gaussiano de media cero con función de covarianza definida no negativa . Sea un espacio de Hilbert del núcleo en reproducción con un núcleo definido positivo . ${\ Displaystyle f}$${\ Displaystyle \ left \ {X_ {t}; t \ in T \ right \}}$${\ Displaystyle K}$${\ Displaystyle {\ mathcal {H}} (R)}$${\ Displaystyle R}$

Luego

${\ Displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] <\ infty}$,

donde y son las matrices de covarianza de todos los posibles pares de puntos, implica ${\ Displaystyle K_ {n}}$${\ Displaystyle R_ {n}}$${\ Displaystyle n}$

${\ Displaystyle \ Pr [f \ in {\ mathcal {H}} (R)] = 1}$.

Y lo que es más,

${\ Displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] = \ infty}$

implica

${\ Displaystyle \ Pr [f \ in {\ mathcal {H}} (R)] = 0}$.

Esto tiene implicaciones significativas cuando , como ${\ Displaystyle K = R}$

${\ Displaystyle \ lim _ {n \ to \ infty} \ operatorname {tr} [R_ {n} R_ {n} ^ {- 1}] = \ lim _ {n \ to \ infty} \ operatorname {tr} [ I] = \ lim _ {n \ to \ infty} n = \ infty}$.

Como tal, casi todas las rutas de muestra de un proceso gaussiano de media cero con un núcleo definido positivo estarán fuera del espacio de Hilbert . ${\ Displaystyle K}$${\ Displaystyle {\ mathcal {H}} (K)}$

Procesos gaussianos linealmente restringidos

Para muchas aplicaciones de interés, ya se proporciona algún conocimiento preexistente sobre el sistema en cuestión. Considérese, por ejemplo, el caso en el que la salida del proceso gaussiano corresponde a un campo magnético; aquí, el campo magnético real está limitado por las ecuaciones de Maxwell y sería deseable una forma de incorporar esta restricción en el formalismo del proceso gaussiano, ya que esto probablemente mejoraría la precisión del algoritmo.

Ya existe un método sobre cómo incorporar restricciones lineales en los procesos gaussianos:

Considere la función de salida (con valor vectorial) que se sabe que obedece a la restricción lineal ( es decir, es un operador lineal) ${\ Displaystyle f (x)}$${\ Displaystyle {\ mathcal {F}} _ {X}}$

${\ Displaystyle {\ mathcal {F}} _ {X} (f (x)) = 0.}$

Entonces la restricción puede cumplirse eligiendo , donde se modela como un proceso gaussiano, y encontrando st ${\ Displaystyle {\ mathcal {F}} _ {X}}$${\ Displaystyle f (x) = {\ mathcal {G}} _ {X} (g (x))}$${\ Displaystyle g (x) \ sim {\ mathcal {GP}} (\ mu _ {g}, K_ {g})}$${\ Displaystyle {\ mathcal {G}} _ {X}}$

${\ Displaystyle {\ mathcal {F}} _ {X} ({\ mathcal {G}} _ {X} (g)) = 0 \ qquad \ forall g.}$

Dado y utilizando el hecho de que los procesos gaussianos están cerrados bajo transformaciones lineales, el proceso gaussiano para obedecer la restricción se convierte en ${\ Displaystyle {\ mathcal {G}} _ {X}}$${\ Displaystyle f}$${\ Displaystyle {\ mathcal {F}} _ {X}}$

${\ Displaystyle f (x) = {\ mathcal {G}} _ {X} g \ sim {\ mathcal {GP}} ({\ mathcal {G}} _ {X} \ mu _ {g}, {\ mathcal {G}} _ {X} K_ {g} {\ mathcal {G}} _ {X '} ^ {T}).}$

Por lo tanto, las restricciones lineales se pueden codificar en la función de covarianza y media de un proceso gaussiano.

Aplicaciones

Un ejemplo de regresión del proceso gaussiano (predicción) en comparación con otros modelos de regresión.

Se puede utilizar un proceso gaussiano como distribución de probabilidad previa sobre funciones en la inferencia bayesiana . Dado cualquier conjunto de N puntos en el dominio deseado de sus funciones, tome una Gaussiana multivariante cuyo parámetro de matriz de covarianza sea ​​la matriz de Gram de sus N puntos con algún kernel deseado , y una muestra de esa Gaussiana. Para la solución del problema de predicción de múltiples salidas, se desarrolló la regresión del proceso gaussiano para la función con valores vectoriales. En este método, se construye una covarianza 'grande', que describe las correlaciones entre todas las variables de entrada y salida tomadas en N puntos en el dominio deseado. Este enfoque se elaboró ​​en detalle para los procesos gaussianos con valores matriciales y se generalizó a procesos con 'colas más pesadas' como los procesos t de Student .

La inferencia de valores continuos con un proceso gaussiano previo se conoce como regresión del proceso gaussiano o kriging ; extender la regresión del proceso gaussiano a múltiples variables objetivo se conoce como cokriging . Los procesos gaussianos son, por tanto, útiles como una poderosa herramienta de interpolación multivariante no lineal .

Los procesos gaussianos también se pueden utilizar en el contexto de modelos mixtos de expertos, por ejemplo. El fundamento fundamental de tal marco de aprendizaje consiste en la suposición de que un mapeo dado no puede ser capturado bien por un solo modelo de proceso gaussiano. En cambio, el espacio de observación se divide en subconjuntos, cada uno de los cuales se caracteriza por una función de mapeo diferente; cada uno de estos se aprende a través de un componente de proceso gaussiano diferente en la mezcla postulada.

Predicción del proceso gaussiano o Kriging

Regresión del proceso gaussiano (predicción) con un núcleo exponencial al cuadrado. El gráfico de la izquierda se extrae de la distribución de funciones anterior. El medio se extrae de la parte posterior. La derecha es la predicción media con una desviación estándar sombreada.

Cuando se trata de un problema de regresión de proceso gaussiano general (Kriging), se supone que para un proceso gaussiano observado en coordenadas , el vector de valores es solo una muestra de una distribución gaussiana multivariada de dimensión igual al número de coordenadas observadas . Por lo tanto, bajo el supuesto de una distribución de media cero , donde es la matriz de covarianza entre todos los pares posibles para un conjunto dado de hiperparámetros θ . Como tal, la probabilidad marginal logarítmica es: ${\ Displaystyle f}$${\ Displaystyle x}$${\ Displaystyle f (x)}$${\ Displaystyle n}$${\ Displaystyle f (x ') \ sim N (0, K (\ theta, x, x'))}$${\ Displaystyle K (\ theta, x, x ')}$${\ Displaystyle (x, x ')}$

${\ Displaystyle \ log p (f (x ') \ mid \ theta, x) = - {\ frac {1} {2}} f (x) ^ {T} K (\ theta, x, x') ^ {-1} f (x ') - {\ frac {1} {2}} \ log \ det (K (\ theta, x, x')) - {\ frac {n} {2}} \ log 2 \Pi }$

y maximizar esta probabilidad marginal hacia θ proporciona la especificación completa del proceso gaussiano f . En este punto, se puede notar brevemente que el primer término corresponde a un término de penalización por la falla de un modelo de ajustar los valores observados y el segundo término a un término de penalización que aumenta proporcionalmente a la complejidad de un modelo. Habiendo especificado θ , hacer predicciones sobre valores no observados en las coordenadas x * es entonces solo una cuestión de extraer muestras de la distribución predictiva donde la estimación media posterior A se define como ${\ Displaystyle f (x ^ {*})}$${\ Displaystyle p (y ^ {*} \ mid x ^ {*}, f (x), x) = N (y ^ {*} \ mid A, B)}$

${\ Displaystyle A = K (\ theta, x ^ {*}, x) K (\ theta, x, x ') ^ {- 1} f (x)}$

y la estimación de la varianza posterior B se define como:

${\ Displaystyle B = K (\ theta, x ^ {*}, x ^ {*}) - K (\ theta, x ^ {*}, x) K (\ theta, x, x ') ^ {- 1 } K (\ theta, x ^ {*}, x) ^ {T}}$

donde es la covarianza entre la nueva coordenada de estimación x * y todas las demás coordenadas observadas x para un vector de hiperparámetro dado θ , y se definen como antes y es la varianza en el punto x * según lo dicta θ . Es importante señalar que prácticamente la estimación media posterior (la "estimación puntual") es solo una combinación lineal de las observaciones ; de manera similar, la varianza de es realmente independiente de las observaciones . Un cuello de botella conocido en la predicción de procesos gaussianos es que la complejidad computacional de la evaluación de inferencia y verosimilitud es cúbica en el número de puntos | x |, y como tal puede volverse inviable para conjuntos de datos más grandes. Los trabajos en procesos gaussianos dispersos, que generalmente se basan en la idea de construir un conjunto representativo para el proceso dado f , tratan de eludir este problema. El método kriging se puede utilizar en el nivel latente de un modelo de efectos mixtos no lineal para una predicción funcional espacial: esta técnica se llama kriging latente. ${\ Displaystyle K (\ theta, x ^ {*}, x)}$${\ Displaystyle K (\ theta, x, x ')}$${\ Displaystyle f (x)}$${\ Displaystyle K (\ theta, x ^ {*}, x ^ {*})}$${\ Displaystyle f (x ^ {*})}$${\ Displaystyle f (x)}$${\ Displaystyle f (x ^ {*})}$${\ Displaystyle f (x)}$

Redes neuronales bayesianas como procesos gaussianos

Las redes neuronales bayesianas son un tipo particular de red bayesiana que resulta de tratar probabilísticamente los modelos de redes neuronales artificiales y el aprendizaje profundo , y asignar una distribución previa a sus parámetros . La computación en redes neuronales artificiales generalmente se organiza en capas secuenciales de neuronas artificiales . La cantidad de neuronas en una capa se denomina ancho de capa. A medida que el ancho de la capa crece, muchas redes neuronales bayesianas se reducen a un proceso gaussiano con un núcleo compositivo de forma cerrada . Este proceso gaussiano se denomina proceso gaussiano de red neuronal (NNGP). Permite que las predicciones de las redes neuronales bayesianas se evalúen de manera más eficiente y proporciona una herramienta analítica para comprender los modelos de aprendizaje profundo .

Problemas computacionales

En aplicaciones prácticas, los modelos de proceso gaussianos a menudo se evalúan en una cuadrícula que conduce a distribuciones normales multivariadas. El uso de estos modelos para la predicción o la estimación de parámetros utilizando la máxima verosimilitud requiere evaluar una densidad gaussiana multivariante, que implica calcular el determinante y la inversa de la matriz de covarianza. Ambas operaciones tienen una complejidad computacional cúbica, lo que significa que incluso para cuadrículas de tamaños modestos, ambas operaciones pueden tener un costo computacional prohibitivo. Este inconveniente condujo al desarrollo de múltiples métodos de aproximación .

Ver también

• Estadísticas lineales de Bayes
• Interpretación bayesiana de regularización
• Kriging
• Campo libre gaussiano
• Proceso de Gauss-Markov
• Kriging mejorado con gradiente (GEK)
• Proceso t de Student

Referencias

enlaces externos

• El sitio web de procesos gaussianos, incluido el texto de los procesos gaussianos para el aprendizaje automático de Rasmussen y Williams
• Una suave introducción a los procesos gaussianos
• Una revisión de los campos aleatorios gaussianos y las funciones de correlación
• Aprendizaje por refuerzo eficiente mediante procesos gaussianos

Software

• GPML: una caja de herramientas integral de Matlab para regresión y clasificación GP
• STK: una pequeña caja de herramientas (Matlab / Octave) para modelado de Kriging y GP
• Módulo Kriging en el marco UQLab (Matlab)
• Función Matlab / Octave para campos gaussianos estacionarios
• Yelp MOE: un motor de optimización de caja negra que utiliza el proceso de aprendizaje gaussiano
• ooDACE : una caja de herramientas flexible de Kriging Matlab orientada a objetos.
• GPstuff: caja de herramientas de proceso gaussiano para Matlab y Octave
• GPy: un marco de procesos gaussianos en Python
• GSTools: una caja de herramientas geoestadísticas, que incluye la regresión del proceso gaussiano, escrita en Python
• Demostración interactiva de regresión del proceso gaussiano
• Biblioteca básica de procesos gaussianos escrita en C ++ 11
• scikit-learn : una biblioteca de aprendizaje automático para Python que incluye regresión y clasificación de procesos gaussianos
• [1] - El kit de herramientas Kriging (KriKit) se desarrolla en el Instituto de Biociencias y Geociencias 1 (IBG-1) de Forschungszentrum Jülich (FZJ)

Tutoriales en vídeo

• Conceptos básicos del proceso gaussiano por David MacKay
• Aprendiendo con procesos gaussianos por Carl Edward Rasmussen
• Inferencia bayesiana y procesos gaussianos por Carl Edward Rasmussen