Grupo simétrico afín - Affine symmetric group

Los grupos simétricos afines son una familia de estructuras matemáticas que describen las simetrías de la recta numérica y el mosaico triangular regular del plano, así como objetos relacionados de dimensiones superiores. Cada uno es una extensión infinita de un grupo simétrico finito , el grupo de permutaciones (reordenamientos) de un conjunto finito. Además de su descripción geométrica, los grupos simétricos afines pueden definirse como conjuntos de permutaciones de los enteros (..., −2, −1, 0, 1, 2, ...) que son periódicos en cierto sentido, o en términos puramente algebraicos como un grupo con ciertos generadores y relaciones . Estas diferentes definiciones permiten la extensión de muchas propiedades importantes de los grupos simétricos finitos al escenario infinito, y se estudian como parte de los campos de la combinatoria y la teoría de la representación .

Definiciones

El grupo simétrico afín puede definirse de manera equivalente como un grupo abstracto por generadores y relaciones, o en términos de modelos geométricos y combinatorios concretos.

Definición algebraica

Una forma de definir grupos es por generadores y relaciones . En este tipo de definición, los generadores son un subconjunto de elementos de grupo que, cuando se combinan, producen todos los demás elementos. Las relaciones de la definición son un sistema de ecuaciones satisfechas por aquellos elementos que implican todas las otras ecuaciones que satisfacen. De esta manera, el grupo simétrico afín es generado por un conjunto ${\ Displaystyle {\ widetilde {S}} _ {n}}$

de n elementos que satisfacen las siguientes relaciones: cuando , ${\ Displaystyle n \ geq 3}$

1. ${\ Displaystyle s_ {i} ^ {2} = 1}$(los generadores son involuciones ),
2. ${\ Displaystyle s_ {i} s_ {j} = s_ {j} s_ {i}}$si j no es uno de , lo que indica que para estos pares de generadores, la operación de grupo es conmutativa , y${\ Displaystyle i-1, i, i + 1}$
3. ${\ Displaystyle s_ {i} s_ {i + 1} s_ {i} = s_ {i + 1} s_ {i} s_ {i + 1}}$.

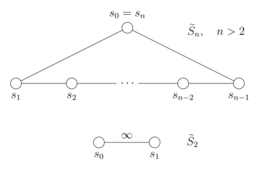
En las relaciones anteriores, los índices se toman módulo n , por lo que la tercera relación incluye como caso particular . (La segunda y tercera relación se denominan a veces relaciones trenzadas .) Cuando , el grupo simétrico afín es el grupo diedro infinito generado por dos elementos sujetos únicamente a las relaciones . ${\ Displaystyle s_ {0} s_ {n-1} s_ {0} = s_ {n-1} s_ {0} s_ {n-1}}$${\ Displaystyle n = 2}$${\ Displaystyle {\ widetilde {S}} _ {2}}$${\ Displaystyle s_ {0}, s_ {1}}$${\ Displaystyle s_ {0} ^ {2} = s_ {1} ^ {2} = 1}$

Estas relaciones se pueden reescribir en la forma especial que define los grupos Coxeter , por lo que los grupos simétricos afines son grupos Coxeter, con el como sus conjuntos generadores Coxeter. Para , el diagrama de Coxeter-Dynkin de es el ciclo n , mientras que para consiste en dos nodos unidos por un borde etiquetado . En estos diagramas, los vértices representan los generadores, que para los grupos de Coxeter deben ser involuciones. Los bordes del ciclo corresponden a las relaciones entre pares de generadores consecutivos, mientras que la ausencia de un borde entre otros pares de generadores indica que se conmutan. ${\ Displaystyle s_ {i}}$${\ Displaystyle n \ geq 3}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle n = 2}$${\ Displaystyle \ infty}$

Definición geométrica

En el espacio euclidiano con coordenadas , el conjunto V de puntos para los cuales forma un (hiper) plano , un subespacio ( n - 1) dimensional. Por cada par de elementos distintos i y j de y cada entero k , el conjunto de puntos en V que satisfacen forma un ( n - 2) subespacio dimensional dentro de V , y hay una única reflexión de V que corrige este subespacio. Entonces, el grupo simétrico afín se puede realizar geométricamente como una colección de mapas de V a sí mismo, las composiciones de estos reflejos. ${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle (x_ {1}, \ ldots, x_ {n})}$${\ Displaystyle x_ {1} + x_ {2} + \ ldots + x_ {n} = 0}$${\ Displaystyle \ {1, \ ldots, n \}}$${\ Displaystyle x_ {i} -x_ {j} = k}$

Dentro de V , el subconjunto de puntos con coordenadas enteras forma el enrejado de raíz de tipo A , Λ . Es el conjunto de todos los vectores enteros tales que . Cada reflejo conserva esta celosía, por lo que la celosía es preservada por todo el grupo. De hecho, se puede definir como el grupo de transformaciones rígidas de V que conservan el retículo Λ . ${\ Displaystyle (a_ {1}, \ ldots, a_ {n})}$${\ Displaystyle a_ {1} + \ ldots + a_ {n} = 0}$${\ Displaystyle {\ widetilde {S}} _ {n}}$

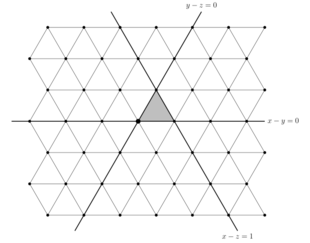
Los subespacios fijos de estos reflejos dividen a V en simples congruentes , llamados nichos . La situación cuando se muestra en la figura; en este caso, la celosía de la raíz es una celosía triangular, con líneas reflectantes que la dividen en nichos de triángulos equiláteros. Sin embargo, para dimensiones más altas, los nichos no son simples simples. ${\ Displaystyle n = 3}$

Para traducir entre las definiciones geométrica y algebraica, arregle un nicho y considere los n hiperplanos que forman su límite. Los reflejos a través de estos hiperplanos limítrofes pueden identificarse con los generadores Coxeter. En particular, hay un hueco único (la alcoba fundamental ) que consta de puntos de tal manera que , que está limitada por los hiperplanos , , ..., y , se ilustra en el caso . Porque , uno puede identificar la reflexión a través del generador Coxeter , y también identificar la reflexión a través del generador . ${\ Displaystyle (x_ {1}, \ ldots, x_ {n})}$${\ Displaystyle x_ {1} \ geq x_ {2} \ geq \ dots \ geq x_ {n} \ geq x_ {1} -1}$${\ Displaystyle x_ {1} -x_ {2} = 0}$${\ Displaystyle x_ {2} -x_ {3} = 0}$${\ Displaystyle x_ {1} -x_ {n} = 1}$${\ Displaystyle n = 3}$${\ Displaystyle i = 1, \ ldots, n-1}$${\ Displaystyle x_ {i} -x_ {i + 1} = 0}$${\ Displaystyle s_ {i}}$${\ Displaystyle x_ {1} -x_ {n} = 1}$${\ Displaystyle s_ {0} = s_ {n}}$

Definición combinatoria

Los elementos del grupo simétrico afín pueden realizarse como un grupo de permutaciones periódicas de los números enteros. En particular, digamos que una función es una permutación afín si ${\ Displaystyle u \ dos puntos \ mathbb {Z} \ to \ mathbb {Z}}$

• es una biyección (cada número entero aparece como el valor de exactamente uno ),${\ Displaystyle u (x)}$${\ Displaystyle x}$
• ${\ Displaystyle u (x + n) = u (x) + n}$para todos los enteros x (la función es equivariante con desplazamiento por ), y${\ Displaystyle n}$
• ${\ Displaystyle u (1) + u (2) + \ ldots + u (n) = 1 + 2 + \ ldots + n}$, el número triangular .${\ Displaystyle n}$

Para cada permutación afín, y más generalmente cada biyección equivariante de desplazamiento, los números deben ser todos módulo n distintos . Una permutación afín está determinada de forma única por su notación de ventana , porque todos los demás valores de se pueden encontrar cambiando estos valores. Por lo tanto, las permutaciones afines también se pueden identificar con tuplas de números enteros que contienen un elemento de cada clase de congruencia módulo ny suma a . ${\ Displaystyle u (1), \ ldots, u (n)}$ ${\ Displaystyle [u (1), \ ldots, u (n)]}$${\ Displaystyle u}$${\ Displaystyle [u (1), \ ldots, u (n)]}$${\ Displaystyle 1 + 2 + \ ldots + n}$

Para traducir entre las definiciones combinatoria y algebraica, uno puede identificar el generador de Coxeter con la permutación afín que tiene notación de ventana , y también identificar el generador con la permutación afín . De manera más general, cada reflejo (es decir, un conjugado de uno de los generadores de Coxeter) se puede describir de manera única de la siguiente manera: para enteros distintos i , j en y un entero arbitrario k , asigna i a j - kn , asigna j a i + kn , y correcciones de todas las entradas no congruente con i o j modulo n . (En términos de la definición geométrica, esto corresponde a la reflexión a través del plano . La correspondencia entre las representaciones geométrica y combinatoria para otros elementos se discute en § Conexión entre las definiciones geométrica y combinatoria ). ${\ Displaystyle i = 1, \ ldots, n-1}$${\ Displaystyle s_ {i}}$${\ Displaystyle [1,2, \ ldots, i-1, i + 1, i, i + 2, \ ldots, n]}$${\ Displaystyle s_ {0} = s_ {n}}$${\ Displaystyle [0,2,3, \ ldots, n-2, n-1, n + 1]}$${\ Displaystyle \ {1, \ ldots, n \}}$${\ Displaystyle x_ {i} -x_ {j} = k}$

Representación como matrices

Se pueden representar permutaciones afines como matrices de permutaciones periódicas infinitas . Si es una permutación afín, se coloca la entrada 1 en la posición de la cuadrícula infinita para cada entero i , y todas las demás entradas son iguales a 0. Como u es una biyección, la matriz resultante contiene exactamente un 1 en cada fila y columna. La condición de periodicidad en el mapa u asegura que la entrada en la posición sea ​​igual a la entrada en la posición para cada par de números enteros . Por ejemplo, una parte de la matriz para la permutación afín se muestra en la figura, con las convenciones de que los 1 se reemplazan por •, los 0 se omiten, los números de filas aumentan de arriba a abajo, los números de columnas aumentan de izquierda a derecha y el límite del cuadro que consta de filas y columnas 1, 2, 3 se dibuja. ${\ Displaystyle u: \ mathbb {Z} \ to \ mathbb {Z}}$${\ Displaystyle (i, u (i))}$${\ Displaystyle \ mathbb {Z} \ times \ mathbb {Z}}$${\ Displaystyle (a, b)}$${\ Displaystyle (a + n, b + n)}$${\ Displaystyle (a, b)}$${\ displaystyle [2,0,4] \ in {\ widetilde {S}} _ {3}}$

Relación con el grupo simétrico finito

El grupo simétrico afín contiene el grupo simétrico finito de permutaciones en elementos como un subgrupo y un grupo cociente . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle n}$

Como subgrupo

Hay una forma canónica de elegir un subgrupo que sea isomorfo al grupo simétrico finito . En términos de la definición algebraica, este es el subgrupo de generado por (excluyendo la reflexión simple ). Geométricamente, esto corresponde al subgrupo de transformaciones que fijan el origen, mientras que combinatoriamente corresponde a las notaciones de ventana para las cuales (es decir, en las que la notación de ventana es la notación de una línea de una permutación finita). ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle s_ {1}, \ ldots, s_ {n-1}}$${\ Displaystyle s_ {0} = s_ {n}}$${\ Displaystyle \ {u (1), \ ldots, u (n) \} = \ {1,2, \ ldots, n \}}$

Si es la ventana de notación de un elemento de esta copia de la norma , su acción sobre el hiperplano V en está dada por permutación de las coordenadas: . (En este artículo, la acción geométrica de permutaciones y permutaciones afines está a la derecha, por lo que, si u y v son dos permutaciones afines, la acción de los rayos UV en un punto se da mediante la aplicación primero u , luego aplicando v .) ${\ Displaystyle u = [u (1), u (2), \ ldots, u (n)]}$${\ Displaystyle S_ {n} \ subconjunto {\ widetilde {S}} _ {n}}$${\ Displaystyle \ mathbb {R} ^ {n}}$${\ Displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n}) \ cdot u = (x_ {u (1)}, x_ {u (2)}, \ ldots, x_ {u ( norte)})}$

También hay muchas copias no estándar de contenido en . Una construcción geométrica consiste en elegir cualquier punto a en Λ (es decir, un vector entero cuyas coordenadas suman 0); el subgrupo de isometrías que fijan a es isomorfo . La construcción combinatoria análoga consiste en elegir cualquier subconjunto A de que contenga un elemento de cada clase de conjugación módulo n y cuyos elementos sumen ; el subgrupo de permutaciones afines que estabilizan A es isomorfo a . ${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {a}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle \ mathbb {Z}}$${\ Displaystyle 1 + 2 + \ ldots + n}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {A}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$

Como cociente

Hay un mapa simple (técnicamente, un homomorfismo de grupo sobreyectivo ) π desde el grupo simétrico finito . En términos de la definición combinatoria, una permutación afín se puede asignar a una permutación reduciendo las entradas de ventana módulo n a elementos de , dejando la notación de una línea de una permutación. La imagen de una permutación afín u se denomina permutación subyacente de u . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle \ {1,2, \ ldots, n \}}$${\ Displaystyle \ pi (u)}$

El mapa π envía el generador de Coxeter a la permutación cuya notación de una línea y notación de ciclo son y , respectivamente. En términos de los generadores de Coxeter de , esto se puede escribir como${\ Displaystyle s_ {0} = [0,2,3,4, \ ldots, n-2, n-1, n + 1]}$${\ Displaystyle [n, 2,3,4, \ ldots, n-2, n-1,1]}$${\ Displaystyle (1 \; n)}$${\ Displaystyle S_ {n}}$${\ Displaystyle \ pi (s_ {0}) = s_ {1} s_ {2} \ cdots s_ {n-2} s_ {n-1} s_ {n-2} \ cdots s_ {2} s_ {1} .}$

El núcleo de π es, por definición, el conjunto de permutaciones afines cuya permutación subyacente es la identidad . Las notaciones de ventana de tales permutaciones afines tienen la forma , donde es un vector entero tal que , es decir, donde . Geométricamente, este núcleo consta de las traslaciones , es decir, las isometrías que desplazan todo el espacio V sin rotarlo ni reflejarlo. En un abuso de notación , el símbolo Λ se usa en este artículo para estos tres conjuntos (vectores enteros en V , permutaciones afines con permutación subyacente de la identidad y traducciones); en los tres entornos, la operación de grupo natural convierte Λ en un grupo abeliano , generado libremente por los n - 1 vectores . ${\ Displaystyle [1-a_ {1} \ cdot n, 2-a_ {2} \ cdot n, \ ldots, n-a_ {n} \ cdot n]}$${\ Displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n})}$${\ Displaystyle a_ {1} + a_ {2} + \ ldots + a_ {n} = 0}$${\ Displaystyle (a_ {1}, \ ldots, a_ {n}) \ in \ Lambda}$${\ Displaystyle \ {(1, -1,0, \ ldots, 0), (0,1, -1, \ ldots, 0), \ ldots, (0, \ ldots, 0,1, -1) \ }}$

La relación entre el núcleo, el grupo simétrico afín y la imagen de π puede expresarse mediante la secuencia corta exacta . Aquí está el núcleo, un grupo abeliano libre con n - 1 generadores. ${\ Displaystyle 0 \ to \ mathbb {Z} ^ {n-1} \ to {\ widetilde {S}} _ {n} \ mathop {\ overset {\ pi} {\ to}} S_ {n} \ to 0}$${\ Displaystyle \ mathbb {Z} ^ {n-1} \ cong \ Lambda}$

Conexión entre las definiciones geométrica y combinatoria

El grupo simétrico afín tiene Λ como un subgrupo normal , y es isomorfo al producto semidirecto${\ Displaystyle {\ widetilde {S}} _ {n}}$

de este subgrupo con el grupo simétrico finito , donde la acción de sobre Λ es por permutación de coordenadas. En consecuencia, cada elemento u de tiene una realización única como un producto donde hay una permutación en la copia estándar de in y es una traducción en . ${\ Displaystyle S_ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle u = r \ cdot t}$${\ Displaystyle r}$${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle t}$${\ Displaystyle \ Lambda}$

Este punto de vista permite una traducción directa entre las definiciones combinatoria y geométrica de : si se escribe dónde y luego la permutación afín

u corresponde al movimiento rígido de V definido por ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle [u (1), \ ldots, u (n)] = [r_ {1} -a_ {1} \ cdot n, \ ldots, r_ {n} -a_ {n} \ cdot n]}$${\ Displaystyle r = [r_ {1}, \ ldots, r_ {n}] = \ pi (u)}$${\ Displaystyle (a_ {1}, a_ {2}, \ ldots, a_ {n}) \ in \ Lambda}$

$${\ Displaystyle (x_ {1}, \ ldots, x_ {n}) \ cdot u = \ left (x_ {r (1)} + a_ {1}, \ ldots, x_ {r (n)} + a_ { n} \ derecha).}$$

Además, como con todo grupo afín de Coxeter, el grupo simétrico afín actúa transitiva y libremente sobre el conjunto de alcobas: para cada dos alcobas, un elemento de grupo único lleva una alcoba a la otra. Por lo tanto, al hacer una elección arbitraria de alcoba , se puede colocar el grupo en correspondencia uno a uno con las alcobas: el

elemento de identidad corresponde a , y todos los demás elementos del grupo g corresponden a la alcoba que es la imagen de debajo de la acción. de g . Esta identificación para se ilustra a la derecha. ${\ Displaystyle A_ {0}}$${\ Displaystyle A_ {0}}$${\ Displaystyle A = A_ {0} \ cdot g}$${\ Displaystyle A_ {0}}$${\ Displaystyle {\ widetilde {S}} _ {3}}$

Ejemplo: n = 2

El grupo simétrico afín actúa sobre la línea V en el plano euclidiano. Los reflejos son a través de las líneas discontinuas. Los vectores del enrejado de la raíz Λ están marcados.${\ Displaystyle {\ widetilde {S}} _ {2}}$

Algebraicamente, es el

grupo diedro infinito , generado por dos generadores sujetos a las relaciones . Todos los demás elementos del grupo se pueden escribir como un producto alterno de copias de y . ${\ Displaystyle {\ widetilde {S}} _ {2}}$${\ Displaystyle s_ {0}, s_ {1}}$${\ Displaystyle s_ {0} ^ {2} = s_ {1} ^ {2} = 1}$${\ Displaystyle s_ {0}}$${\ Displaystyle s_ {1}}$

Combinatoriamente, la permutación afín tiene notación de ventana , correspondiente a la biyección para cada entero

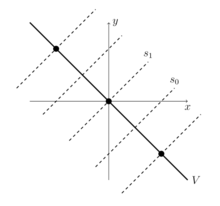
k . La permutación afín tiene notación de ventana , correspondiente a la biyección para cada entero k . Otros elementos tienen las siguientes notaciones de ventana: ${\ Displaystyle s_ {1}}$${\ Displaystyle [2,1]}$${\ Displaystyle 2k \ mapsto 2k-1,2k-1 \ mapsto 2k}$${\ Displaystyle s_ {0}}$${\ Displaystyle [0,3]}$${\ Displaystyle 2k \ mapsto 2k + 1,2k + 1 \ mapsto 2k}$

• ${\ Displaystyle \ overbrace {s_ {0} s_ {1} \ cdots s_ {0} s_ {1}} ^ {2k \, {\ text {factores}}} = [1 + 2k, 2-2k],}$
• ${\ Displaystyle \ overbrace {s_ {1} s_ {0} \ cdots s_ {1} s_ {0}} ^ {2k \, {\ text {factores}}} = [1-2k, 2 + 2k],}$
• ${\ Displaystyle \ overbrace {s_ {0} s_ {1} \ cdots s_ {0}} ^ {2k + 1 \, {\ text {factores}}} = [2 + 2k, 1-2k],}$
• ${\ Displaystyle \ overbrace {s_ {1} s_ {0} \ cdots s_ {1}} ^ {2k + 1 \, {\ text {factores}}} = [2-2 (k + 1), 1 + 2 (k + 1)].}$

Geométricamente, el espacio V es la recta con ecuación en el plano euclidiano . El enrejado de la raíz dentro de

V consta de esos pares para la integral a . El generador de Coxeter actúa sobre V por reflexión a través de la línea (es decir, a través del origen); el generador actúa sobre V por reflexión a través de la línea (es decir, a través del punto . Es natural identificar la línea V con la línea real , enviando el punto al número real 2 x . Con esta identificación, la red raíz consiste en de los enteros pares, el hueco fundamental es el intervalo [0, 1] , el elemento actúa por traslación por k para cualquier entero k , y la reflexión se refleja a través del punto - k para cualquier entero k . ${\ Displaystyle x + y = 0}$${\ Displaystyle \ mathbb {R} ^ {2}}$${\ Displaystyle (a, -a)}$${\ Displaystyle s_ {1}}$${\ Displaystyle x = y}$${\ Displaystyle s_ {0}}$${\ Displaystyle x = y + 1}$${\ Displaystyle \ left ({\ tfrac {1} {2}}, - {\ tfrac {1} {2}} \ right)}$${\ Displaystyle \ mathbb {R} ^ {1}}$${\ Displaystyle (x, -x)}$${\ Displaystyle (s_ {1} s_ {0}) ^ {k}}$${\ Displaystyle s_ {1} (s_ {0} s_ {1}) ^ {k}}$

Estadísticas de permutación y patrones de permutación

Muchas estadísticas de permutación y otras características de la combinatoria de permutaciones finitas pueden extenderse al caso afín.

Descensos, longitud e inversiones

La longitud de un elemento

g de un Coxeter grupo G es el menor número k tal que g se puede escribir como un producto de k generadores de Coxeter de G . ${\ Displaystyle \ ell (g)}$${\ Displaystyle g = s_ {i_ {1}} \ cdots s_ {i_ {k}}}$

Geométricamente, la longitud de un elemento g en es el número de reflejar hiperplanos que separan y , donde es la alcoba fundamental (el simplex delimitada por los hiperplanos reflectantes de los generadores de Coxeter ). (De hecho, lo mismo es cierto para cualquier grupo afín de Coxeter). ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle A_ {0}}$${\ Displaystyle A_ {0} \ cdot g}$${\ Displaystyle A_ {0}}$${\ Displaystyle s_ {0}, s_ {1}, \ ldots, s_ {n-1}}$

Combinatoriamente, la longitud de una permutación afín se codifica en términos de una noción apropiada de inversiones . En particular, uno tiene por una permutación afín u que

$${\ Displaystyle \ ell (u) = \ # \ left \ {(i, j) \ colon i \ in \ {1, \ ldots, n \}, i <j, {\ text {y}} u (i )> u (j) \ right \}.}$$

Alternativamente, es el número de clases de equivalencia de pares tal que y bajo la relación de equivalencia si para algún entero k . ${\ Displaystyle (i, j) \ in \ mathbb {Z} \ times \ mathbb {Z}}$${\ Displaystyle i <j}$${\ Displaystyle u (i)> u (j)}$${\ Displaystyle (i, j) \ equiv (i ', j')}$${\ Displaystyle (i-i ', j-j') = (kn, kn)}$

La función generadora de la longitud en es ${\ Displaystyle {\ widetilde {S}} _ {n}}$

$${\ Displaystyle \ sum _ {g \ in {\ widetilde {S}} _ {n}} q ^ {\ ell (g)} = {\ frac {1-q ^ {n}} {(1-q) ^ {n}}}.}$$

De manera similar, se puede definir un análogo afín de descensos en permutaciones: digamos que una permutación afín u tiene un descenso en la posición i si . (Por periodicidad,

u tiene un descenso en la posición i si y solo si tiene un descenso en la posición para todos los enteros k ). ${\ Displaystyle u (i)> u (i + 1)}$${\ Displaystyle i + kn}$

Algebraicamente, los descensos corresponden a los descensos rectos en el sentido de grupos de Coxeter; es decir, i es un descenso de u si y solo si . Los descensos a la izquierda (es decir, aquellos índices

i tales que son los descensos de la permutación afín inversa ; de manera equivalente, son los valores i tales que i aparece antes que i - 1 en la secuencia . ${\ Displaystyle \ ell (u \ cdot s_ {i}) <\ ell (u)}$${\ Displaystyle \ ell (s_ {i} \ cdot u) <\ ell (u)}$${\ Displaystyle u ^ {- 1}}$ ${\ Displaystyle \ ldots, u (-2), u (-1), u (0), u (1), u (2), \ ldots}$

Geométricamente, i es un descenso de u si y solo si el hiperplano fijo de separa los nichos y . ${\ Displaystyle s_ {i}}$${\ Displaystyle A_ {0}}$${\ Displaystyle A_ {0} \ cdot u}$

Debido a que solo hay un número finito de posibilidades para el número de descensos de una permutación afín, pero infinitas permutaciones afines, no es posible formar ingenuamente una función generadora para permutaciones afines por número de descensos (un análogo afín de los polinomios eulerianos ). Una posible resolución es considerar descensos afines (equivalentemente, descensos cíclicos) en el grupo simétrico finito . Otro es considerar simultáneamente la longitud y el número de descensos de una permutación afín. La función generadora de estas estadísticas simultáneamente para todo

n es ${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$

$${\ Displaystyle \ sum _ {n \ geq 1} {\ frac {x ^ {n}} {1-q ^ {n}}} \ sum _ {w \ in {\ widetilde {S}} _ {n} } t ^ {\ operatorname {des} (w)} q ^ {\ ell (w)} = \ left [{\ frac {x \ cdot {\ frac {\ partial} {\ partial {x}}} \ log (\ exp (x; q))} {1-t \ exp (x; q)}} \ right] _ {x \ mapsto x {\ frac {1-t} {1-q}}}}$$

donde des ( w ) es el número de descensos de la permutación afín w y es la función q -exponencial . ${\ Displaystyle \ exp (x; q) = \ sum _ {n \ geq 0} {\ frac {x ^ {n} (1-q) ^ {n}} {(1-q) (1-q ^ {2}) \ cdots (1-q ^ {n})}}}$

Tipo de ciclo y longitud de reflexión

Cualquier biyección divide los enteros en una lista (posiblemente infinita) de ciclos (posiblemente infinitos): para cada entero

i , el ciclo que contiene i es la secuencia donde la exponenciación representa la composición funcional. Por ejemplo, la permutación afín con notación de ventana contiene los dos ciclos infinitos y también infinitos ciclos finitos para cada uno . Los ciclos de una permutación afín corresponden a los ciclos de la permutación subyacente de una manera obvia: en el ejemplo anterior, con la permutación subyacente , el primer ciclo infinito corresponde al ciclo (1), el segundo corresponde al ciclo (45) y el todos los ciclos finitos corresponden al ciclo (23). ${\ Displaystyle u: \ mathbb {Z} \ to \ mathbb {Z}}$${\ Displaystyle (\ ldots, u ^ {- 2} (i), u ^ {- 1} (i), i, u (i), u ^ {2} (i), \ ldots)}$${\ Displaystyle {\ widetilde {S}} _ {5}}$${\ displaystyle [6,3,2,0,4]}$${\ Displaystyle (\ ldots, -9, -4,1,6,11, \ ldots)}$${\ Displaystyle (\ ldots, 10,9,5,4,0, -1, -5 \ ldots)}$${\ Displaystyle (5k + 2,5k + 3)}$${\ Displaystyle k \ in \ mathbb {Z}}$${\ displaystyle [1,3,2,5,4] = (1) (23) (45)}$

Para una permutación afín u , las siguientes condiciones son equivalentes: todos los ciclos de u son finitos, u tiene un orden finito y la acción geométrica de u en el espacio V tiene al menos un punto fijo.

La longitud de

reflexión de un elemento u de es el número más pequeño k tal que existen reflexiones tales que . (En el grupo simétrico, las reflexiones son transposiciones, y la longitud de reflexión de una permutación es u , donde es el número de ciclos de u .) En ( Lewis et al.2019 ), se demostró la siguiente fórmula para la longitud de reflexión de una permutación afín u : para cada ciclo de u , defina el peso como el entero k tal que las entradas consecutivas módulo n congruentes difieran exactamente en kn . (Por ejemplo, en la permutación anterior, el primer ciclo infinito tiene peso 1 y el segundo ciclo infinito tiene peso -1; todos los ciclos finitos tienen peso 0). Forme una tupla de pesos de ciclo de u (el conteo se traduce del mismo ciclo por múltiplos de n solo una vez), y defina la nulidad como el tamaño de la partición de conjunto más pequeña de esta tupla de modo que cada parte sume 0. (En el ejemplo anterior, la tupla es y la nulidad es 2, ya que uno puede tomar la partición .) Entonces la longitud de reflexión de u es ${\ Displaystyle \ ell _ {R} (u)}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle r_ {1}, \ ldots, r_ {k}}$${\ Displaystyle u = r_ {1} \ cdots r_ {k}}$${\ Displaystyle nc (u)}$${\ Displaystyle c (u)}$${\ displaystyle [5,2,0,3]}$ ${\ Displaystyle \ nu (u)}$${\ displaystyle (1, -1,0)}$${\ displaystyle (1, -1), (0)}$

$${\ Displaystyle \ ell _ {R} (u) = n-2 \ nu (u) + c (\ pi (u)),}$$

donde es la permutación subyacente de u . ${\ Displaystyle \ pi (u)}$

Para cada permutación afín u , hay una opción del subgrupo W de tal manera que , y de la forma estándar implica este producto semidirecto, uno tiene . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle W \ cong S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n} = W \ ltimes \ Lambda}$${\ Displaystyle u = w \ cdot t}$${\ Displaystyle \ ell _ {R} (u) = \ ell _ {R} (w) + \ ell _ {R} (t)}$

Elementos totalmente conmutativos y evitación de patrones

Una palabra reducida para un elemento g de un grupo Coxeter es una tupla de generadores Coxeter de longitud mínima posible tal que . El elemento

g se denomina totalmente conmutativo si se puede transformar cualquier palabra reducida en cualquier otra intercambiando secuencialmente pares de factores que conmutan. Por ejemplo, en el grupo simétrico finito , el elemento es completamente conmutativo, ya que sus dos palabras reducidas y se pueden conectar intercambiando factores de conmutación, pero no es completamente conmutativo porque no hay forma de llegar a la palabra reducida a partir de la palabra reducida por conmutaciones. ${\ Displaystyle (s_ {i_ {1}}, \ ldots, s_ {i _ {\ ell (g)}})}$${\ Displaystyle g = s_ {i_ {1}} \ cdots s_ {i _ {\ ell (g)}}}$${\ Displaystyle S_ {4}}$${\ Displaystyle 2143 = (12) (34)}$${\ Displaystyle (s_ {1}, s_ {3})}$${\ Displaystyle (s_ {3}, s_ {1})}$${\ Displaystyle 3214 = (13) (2) (4)}$${\ Displaystyle (s_ {2}, s_ {1}, s_ {2})}$${\ Displaystyle (s_ {1}, s_ {2}, s_ {1})}$

Billey, Jockusch y Stanley (1993) demostraron que en el grupo simétrico finito , una permutación es completamente conmutativa si y solo si evita el

patrón de permutación 321, es decir, si y solo si su notación de una línea no contiene decrecientes de tres términos. subsecuencia. En ( Green 2002 ), este resultado se extendió a las permutaciones afines: una permutación afín u es completamente conmutativa si y solo si no existen enteros tales que . ${\ Displaystyle S_ {n}}$${\ Displaystyle i <j <k}$${\ Displaystyle u (i)> u (j)> u (k)}$

El número de permutaciones afines que evitan un solo patrón p es finito si y solo si p evita el patrón 321, por lo que en particular hay infinitas permutaciones afines totalmente conmutativas. Estos fueron enumerados por longitud en ( Hanusa & Jones 2010 ).

Subgrupos parabólicos y otras estructuras

Los subgrupos parabólicos de y sus representantes de clases laterales ofrecen una rica estructura combinatoria. Otros aspectos del grupo simétrico afín, como su orden de Bruhat y la teoría de la representación, también pueden entenderse mediante modelos combinatorios. ${\ Displaystyle {\ widetilde {S}} _ {n}}$

Subgrupos parabólicos, representantes de coset

Diagrama de ábaco de la permutación afín [−5, 0, 6, 9].

Un

subgrupo parabólico estándar de un grupo Coxeter es un subgrupo generado por un subconjunto de su grupo electrógeno Coxeter. Los subgrupos parabólicos máximos son aquellos que provienen de omitir un solo generador Coxeter. En , todos los subgrupos parabólicos máximos son isomorfos al grupo simétrico finito . El subgrupo generado por el subconjunto consiste en aquellas permutaciones afines que estabilizan el intervalo , es decir, que mapean cada elemento de este intervalo a otro elemento del intervalo. ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle \ {s_ {0}, \ ldots, s_ {n-1} \} \ smallsetminus \ {s_ {i} \}}$${\ Displaystyle [i + 1, i + n]}$

Los subgrupos parabólicos no máximos de son todos isomorfos a subgrupos parabólicos de , es decir, a un subgrupo de Young para algunos enteros positivos con suma n . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle S_ {n}}$ ${\ Displaystyle S_ {a_ {1}} \ times \ cdots \ times S_ {a_ {k}}}$${\ Displaystyle a_ {1}, \ ldots, a_ {k}}$

Para un elemento fijo i de , dejar que sea el subconjunto propio máxima de generadores de Coxeter omitiendo , y dejar que denote el subgrupo parabólico generada por J . Cada coset tiene un elemento único de longitud mínima. La colección de tales representantes, denotada , consta de las siguientes permutaciones afines: ${\ Displaystyle \ {0, \ ldots, n-1 \}}$${\ Displaystyle J = \ {s_ {0}, \ ldots, s_ {n-1} \} \ smallsetminus \ {s_ {i} \}}$${\ Displaystyle s_ {i}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {J}}$ ${\ Displaystyle g \ cdot ({\ widetilde {S}} _ {n}) _ {J}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) ^ {J}}$

En el caso particular de que , por lo que es la copia estándar de inside , los elementos de pueden naturalmente estar representados por diagramas de ábaco : los números enteros están dispuestos en una franja infinita de ancho n , aumentando secuencialmente a lo largo de filas y luego de arriba a abajo; los enteros están encerrados en un círculo si se encuentran directamente encima de una de las entradas de ventana del representante de la clase lateral mínima. Por ejemplo, el representante de la clase lateral mínima está representado por el diagrama del ábaco a la derecha. Para calcular la longitud del representante del diagrama del ábaco, se suma el número de números sin círculo que son más pequeños que la última entrada encerrada en un círculo en cada columna. (En el ejemplo que se muestra, esto da .) ${\ Displaystyle J = \ {s_ {1}, \ ldots, s_ {n-1} \}}$${\ Displaystyle ({\ widetilde {S}} _ {n}) _ {J} \ cong S_ {n}}$${\ Displaystyle S_ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ displaystyle ({\ widetilde {S}} _ {n}) ^ {J} \ cong {\ widetilde {S}} _ {n} / S_ {n}}$${\ Displaystyle u = [- 5,0,6,9]}$${\ Displaystyle 5 + 3 + 0 + 1 = 9}$

Otros modelos combinatorios de representantes de clase lateral de longitud mínima para se pueden dar en términos de particiones centrales ( particiones enteras en las que ninguna longitud de gancho es divisible por n ) o particiones limitadas (particiones enteras en las que ninguna parte es mayor que n - 1 ). Bajo estas correspondencias, se puede demostrar que el orden de Bruhat débil en es isomorfo a un cierto subposet del enrejado de Young . ${\ displaystyle {\ widetilde {S}} _ {n} / S_ {n}}$${\ displaystyle {\ widetilde {S}} _ {n} / S_ {n}}$

Orden de Bruhat

El orden de Bruhat en tiene la siguiente realización combinatoria. Si u es una permutación afín y i y j son números enteros, definir para ser el número de enteros un tal que y . (Por ejemplo, con , uno tiene : los tres valores relevantes son , que son respectivamente mapeados por u a 1, 2 y 4.) Luego, para dos permutaciones afines u , v , uno tiene eso en orden de Bruhat si y solo si para todos los enteros i , j . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle u [i, j]}$${\ Displaystyle a \ leq i}$${\ Displaystyle u (a) \ geq j}$${\ Displaystyle u = [2,0,4] \ in {\ widetilde {S}} _ {3}}$${\ Displaystyle u [3,1] = 3}$${\ Displaystyle a = 0,1,3}$${\ Displaystyle u \ leq v}$${\ Displaystyle u [i, j] \ leq v [i, j]}$

Teoría de la representación y una correspondencia afín de Robinson-Schensted

En el grupo simétrico finito, la correspondencia de Robinson-Schensted da una biyección entre el grupo y los pares de cuadros de Young estándar de la misma forma. Esta biyección juega un papel central en la combinatoria y la teoría de la representación del grupo simétrico . Por ejemplo, en el lenguaje de la teoría de Kazhdan-Lusztig , dos permutaciones se encuentran en la misma celda izquierda si y solo si sus imágenes bajo Robinson-Schensted tienen el mismo cuadro Q , y en la misma celda derecha si y solo si sus imágenes tienen el mismo cuadro. mismo cuadro P . En ( Shi 1986 ), J.-Y. Shi mostró que las celdas de la izquierda para están indexadas por tabloides , y en ( Shi 1991 ) dio un algoritmo para calcular el tabloide análogo al cuadro P para una permutación afín. En ( Chmutov, Pylyavskyy & Yudovina 2018 ), los autores ampliaron el trabajo de Shi para dar un mapa biyectivo entre y triples que consta de dos tabloides de la misma forma y un vector entero cuyas entradas satisfacen ciertas desigualdades. Su procedimiento utiliza la representación matricial de permutaciones afines y generaliza la construcción de sombras de Viennot (1977) . ${\ Displaystyle (P, Q)}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle (P, Q, \ rho)}$

Realizaciones inversas

En algunas situaciones, uno puede desear considerar la acción del grupo simétrico afín sobre o sobre nichos que es inversa a la dada anteriormente. Describimos estas realizaciones alternativas ahora. ${\ Displaystyle \ mathbb {Z}}$

En la acción combinatoria de on , el generador actúa cambiando los valores i e i + 1 . En la acción inversa, cambia las entradas en las posiciones i e i + 1 . Del mismo modo, la acción de una reflexión general será la de cambiar las entradas en las posiciones j - kn y i + kn para cada k , la fijación de todas las entradas en las posiciones no congruente con i o j modulo n . (En el grupo simétrico finito , la distinción análoga es entre las formas activa y pasiva de una permutación). ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle \ mathbb {Z}}$${\ Displaystyle s_ {i}}$ ${\ Displaystyle S_ {n}}$

En la acción geométrica de , el generador actúa sobre un nicho A reflejándolo a través de uno de los planos delimitadores del nicho fundamental A ₀ . En la acción inversa, en cambio, refleja A a través de uno de sus propios planos delimitadores. Desde esta perspectiva, una palabra reducidas corresponde a un pie hueco en el espacio teselado V . ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle s_ {i}}$

Relación con otros objetos matemáticos

El grupo simétrico afín está estrechamente relacionado con una variedad de otros objetos matemáticos.

Patrones de malabarismo

En ( Ehrenborg y Readdy 1996 ), se da una correspondencia entre permutaciones afines y patrones de malabarismo codificados en una versión de la notación de intercambio de sitios . Aquí, un patrón de malabarismo del período n es una secuencia de números enteros no negativos (con ciertas restricciones) que captura el comportamiento de las pelotas lanzadas por un malabarista, donde el número indica el tiempo que el i- ésimo lanzamiento pasa en el aire (equivalentemente, el altura del lanzamiento). El número b de bolas en el patrón es el promedio . La correspondencia de Ehrenborg-Readdy asocia a cada patrón de malabarismo del período n la función definida por ${\ Displaystyle (a_ {1}, \ ldots, a_ {n})}$${\ Displaystyle a_ {i}}$${\ Displaystyle b = {\ frac {a_ {1} + \ ldots + a_ {n}} {n}}}$${\ Displaystyle {\ bf {a}} = (a_ {1}, \ ldots, a_ {n})}$${\ Displaystyle w _ {\ bf {a}} \ colon \ mathbb {Z} \ to \ mathbb {Z}}$

donde los índices de la secuencia a se toman módulo n . Entonces hay una permutación afín en y, además, toda permutación afín surge de un patrón de malabarismo de esta manera. Bajo esta biyección, la longitud de la permutación afín está codificada por una estadística natural en el patrón de malabarismo: uno tiene ${\ Displaystyle w _ {\ bf {a}}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$ donde es el número de cruces (hasta la periodicidad) en el diagrama de arco de a . Esto permite una prueba elemental de la función generadora de permutaciones afines por longitud. ${\ Displaystyle \ operatorname {cruz} ({\ bf {a}})}$

Por ejemplo, el patrón de malabarismo 441 (ilustrado a la derecha) tiene y . Por tanto, corresponde a la permutación afín . El patrón de malabarismo tiene cuatro cruces y la permutación afín tiene longitud . ${\ Displaystyle n = 3}$${\ Displaystyle b = {\ frac {4 + 4 + 1} {3}} = 3}$${\ Displaystyle w_ {441} = [1 + 4-3,2 + 4-3,3 + 1-3] = [2,3,1]}$${\ Displaystyle \ ell (w_ {441}) = (3-1) \ cdot 3-4 = 2}$

Se pueden utilizar técnicas similares para derivar la función generadora de los representantes de las clases laterales mínimas por longitud. ${\ displaystyle {\ widetilde {S}} _ {n} / S_ {n}}$

Grupos de reflexión complejos

En un espacio de producto interno real de dimensión finita , una reflexión es una transformación lineal que fija un hiperplano lineal puntualmente y niega el vector ortogonal al plano. Esta noción puede extenderse a espacios vectoriales sobre otros campos . En particular, en un espacio de producto interno complejo, un reflejo es una transformación unitaria T de orden finito que fija un hiperplano. Esto implica que los vectores ortogonales al hiperplano son vectores propios de T , y el valor propio asociado es una raíz de unidad compleja . Un grupo de reflexión complejo es un grupo finito de transformaciones lineales en un espacio vectorial complejo generado por reflexiones.

Los grupos de reflexión complejos fueron clasificados por completo por Shephard y Todd (1954) : cada grupo de reflexión complejo es isomorfo a un producto de grupos de reflexión complejos irreductibles, y cada irreducible pertenece a una familia infinita (donde

m , p y n son números enteros positivos tal que p divide m ) o es uno de los otros 34 ejemplos (los llamados "excepcionales"). El grupo es el grupo simétrico generalizado : algebraicamente, es el producto de corona del grupo cíclico con el grupo simétrico . Concretamente, los elementos del grupo pueden estar representados por matrices monomiales (matrices que tienen una entrada distinta de cero en cada fila y columna) cuyas entradas distintas de cero son todas las raíces m ésimas de la unidad. Los grupos son subgrupos de y, en particular, el grupo consta de aquellas matrices en las que el producto de las entradas distintas de cero es igual a 1. ${\ Displaystyle G (m, p, n)}$${\ Displaystyle G (m, 1, n)}$ ${\ Displaystyle (\ mathbb {Z} / m \ mathbb {Z}) \ wr S_ {n}}$ ${\ Displaystyle \ mathbb {Z} / m \ mathbb {Z}}$${\ Displaystyle S_ {n}}$${\ Displaystyle G (m, p, n)}$${\ Displaystyle G (m, 1, n)}$${\ Displaystyle G (m, m, n)}$

En ( Shi 2002 ), Shi mostró que el grupo simétrico afín es una cobertura genérica de la familia , en el siguiente sentido: para cada entero positivo

m , hay una sobreyección de a , y estos mapas son compatibles con las sobreyecciones naturales cuando ese provienen de elevar cada entrada a la m / p ésima potencia. Además, estas proyecciones respetan la estructura del grupo de reflexión, en el sentido de que la imagen de cada reflexión en bajo es un reflejo en ; y de manera similar cuando la imagen del elemento Coxeter estándar en es un elemento Coxeter en . ${\ Displaystyle \ left \ {G (m, m, n) \ colon m \ geq 1 \ right \}}$${\ Displaystyle \ pi _ {m}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle G (m, m, n)}$${\ Displaystyle G (m, m, n) \ twoheadrightarrow G (p, p, n)}$${\ Displaystyle p \ mid m}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle \ pi _ {m}}$${\ Displaystyle G (m, m, n)}$${\ Displaystyle m> 1}$ ${\ Displaystyle s_ {0} \ cdot s_ {1} \ cdots s_ {n-1}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle G (m, m, n)}$

Álgebras de mentiras afines

Cada grupo afín de Coxeter está asociado a un álgebra de Lie afín , un cierto

álgebra no asociativa de dimensión infinita con propiedades teóricas de representación inusualmente agradables. En esta asociación, el grupo Coxeter surge como un grupo de simetrías del espacio raíz del álgebra de Lie (el dual de la subálgebra de Cartan). En la clasificación de álgebras de Lie afines, la asociada a es de tipo (sin torcer) , con matriz de Cartan para y ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle A_ {n-1} ^ {(1)}}$ ${\ displaystyle {\ begin {bmatrix} 2 y -2 \\ - 2 y 2 \ end {bmatrix}}}$${\ Displaystyle n = 2}$

$${\ displaystyle {\ begin {bmatrix} 2 & -1 & 0 & \ cdots & 0 & -1 \\ - 1 & 2 & -1 & \ cdots & 0 & 0 \\ 0 & -1 & 2 & \ cdots & 0 & 0 \\\ vdots & \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & 0 & 0 & \ cdots & 2 & -1 \\ - 1 & 0 & 0 & \ cdots & -1 & 2 \ end {bmatrix}}}$$

(una matriz circulante ) para . ${\ Displaystyle n> 2}$

Como otras álgebras de Kac-Moody , las

álgebras de Lie afines satisfacen la fórmula de caracteres de Weyl-Kac , que expresa los caracteres del álgebra en términos de sus pesos más altos . En el caso de las álgebras de Lie afines, las identidades resultantes son equivalentes a las identidades de Macdonald . En particular, para el álgebra de tipo afín de Lie , asociada al grupo simétrico afín , la identidad de Macdonald correspondiente es equivalente al producto triple de Jacobi . ${\ Displaystyle A_ {1} ^ {(1)}}$${\ Displaystyle {\ widetilde {S}} _ {2}}$

Grupo simétrico afín extendido

El grupo simétrico afín es un subgrupo del grupo simétrico afín extendido . El grupo extendido es isomorfo al producto de la corona . Sus elementos son

permutaciones afines extendidas : biyecciones tales que para todos los enteros x . A diferencia del grupo simétrico afín, el grupo simétrico afín extendido no es un grupo Coxeter. Sin embargo, tiene un grupo electrógeno natural que extiende el grupo electrógeno Coxeter para : el operador de turno cuya notación de ventana es genera el grupo extendido con los reflejos simples, sujeto a las relaciones adicionales . ${\ Displaystyle \ mathbb {Z} \ wr S_ {n}}$${\ Displaystyle u \ dos puntos \ mathbb {Z} \ to \ mathbb {Z}}$${\ Displaystyle u (x + n) = u (x) + n}$${\ Displaystyle {\ widetilde {S}} _ {n}}$ ${\ Displaystyle \ tau}$${\ Displaystyle \ tau = [2,3, \ ldots, n, n + 1]}$${\ Displaystyle \ tau s_ {i} \ tau ^ {- 1} = s_ {i + 1}}$

Combinatoria de otros grupos afines de Coxeter

La acción geométrica del grupo simétrico afín lo ubica naturalmente en la familia de

grupos Coxeter afines , todos los cuales tienen una acción geométrica similar. La descripción combinatoria de los también puede extenderse a muchos de estos grupos: en Eriksson y Eriksson (1998) , se da una descripción axiomática de ciertos grupos de permutación que actúan sobre (los "grupos de George", en honor a George Lusztig ), y Se muestra que son exactamente los grupos de Coxeter "clásicos" de tipos finitos y afines A, B, C y D. Por tanto, las interpretaciones combinatorias de descensos, inversiones, etc., se trasladan en estos casos. Los modelos de ábaco de representantes de clase lateral de longitud mínima para cocientes parabólicos también se han extendido a este contexto. ${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle {\ widetilde {S}} _ {n}}$${\ Displaystyle \ mathbb {Z}}$

Notas

Este artículo fue adaptado de la siguiente fuente bajo una licencia CC BY 4.0 ( 2021 ) ( informes de los revisores ): Joel Brewster Lewis (21 de abril de 2021). "Grupo simétrico afín" (PDF) . WikiJournal of Science . 4 (1): 3. doi : 10.15347 / WJS / 2021.003 . ISSN  2470-6345 . Wikidata  Q100400684 .

Referencias

• Beazley, Elizabeth; Nichols, Margaret; Park, Min Hae; Shi, XiaoLin; Youcis, Alexander (2015), "Proyecciones biyectivas sobre cocientes parabólicos de grupos de Weyl afines", J. Algebr. Peine. , 41 (4): 911–948, doi : 10.1007 / s10801-014-0559-9
• Berg, Chris; Jones, Brant; Vazirani, Monica (2009), "Una biyección en particiones centrales y un cociente parabólico del grupo simétrico afín", J. Combin. Teoría Ser. A , 116 (8): 1344–1360, arXiv : 0804.1380 , doi : 10.1016 / j.jcta.2009.03.013 , S2CID  3032099
• Billey, Sara C .; Jockusch, William; Stanley, Richard P. (1993), "Algunas propiedades combinatorias de los polinomios de Schubert", J. Algebr. Peine. , 2 (4): 345–374, doi : 10.1023 / A: 1022419800503
• Björner, Anders ; Brenti, Francesco (1996), "Permutaciones afines de tipo A", Electron. J. Combin. , 3 (2): R18, doi : 10.37236 / 1276
• Björner, Anders ; Brenti, Francesco (2005), Combinatoria de grupos Coxeter , Springer, ISBN 978-3540-442387
• Cameron, Peter J. (1994), Combinatoria: temas, técnicas, algoritmos , Cambridge University Press, ISBN 978-0-521-45761-3
• Chmutov, Michael; Pylyavskyy, Pavlo; Yudovina, Elena (2018), "Construcción matriz-bola de correspondencia afín Robinson-Schensted", Selecta Math. , Serie nueva, 24 (2): 667–750, arXiv : 1511.05861 , doi : 10.1007 / s00029-018-0402-6 , S2CID  119086049
• Clark, Eric; Ehrenborg, Richard (2011), "Excedances of affine permutations", Advances in Applied Mathematics , 46 (1-4): 175-191, doi : 10.1016 / j.aam.2009.12.006
• Crites, Andrew (2010), "Enumeración de la evitación de patrones para permutaciones afines", Electron. J. Combin. , 17 (1): R127, arXiv : 1002.1933 , doi : 10.37236 / 399
• Ehrenborg, Richard ; Readdy, Margaret (1996), "Malabares y aplicaciones a q -análogos", Matemáticas discretas. , 157 (1–3): 107–125, CiteSeerX  10.1.1.8.6684 , doi : 10.1016 / S0012-365X (96) 83010-X
• Eriksson, Henrik; Eriksson, Kimmo (1998), "Grupos de Weyl afines como permutaciones infinitas", Electron. J. Combin. , 5 : R18, doi : 10.37236 / 1356
• Green, RM (2002), "Sobre 321: evitar permutaciones en grupos de Weyl afines", J. Algebr. Peine. , 15 (3): 241–252, doi : 10.1023 / A: 1015012524524
• Hanusa, Christopher RH; Jones, Brant C. (2010), "La enumeración de permutaciones afines totalmente conmutativas", Eur. J. Comb. , 31 (5): 1342-1359, arXiv : 0907.0709 , doi : 10.1016 / j.ejc.2009.11.010 , S2CID  789357
• Hanusa, Christopher RH; Jones, Brant C. (2012), "Modelos de ábaco para cocientes parabólicos de grupos de Weyl afines", J. Algebra , 361 : 134-162, doi : 10.1016 / j.jalgebra.2012.03.029
• Humphreys, James E. (1990), Grupos de reflexión y grupos Coxeter , Cambridge University Press, ISBN 0-521-37510-X
• Kac, Victor G. (1990), Álgebras de Lie de dimensión infinita (3a ed.), Cambridge University Press, ISBN 0-521-46693-8
• Knutson, Allen ; Lam, Thomas; Speyer, David E. (2013), "Variedades de Positroides: malabares y geometría", Compos. Matemáticas. , 149 (10): 1710–1752, doi : 10.1112 / S0010437X13007240
• Lam, Thomas (2015), "La forma de un elemento del grupo Weyl afín al azar y particiones centrales aleatorias", Ann. Probab. , 43 (4): 1643–1662, doi : 10.1214 / 14-AOP915
• Lapointe, Luc; Morse, Jennifer (2005), "Cuadros en núcleos, palabras reducidas para permutaciones afines y expansiones -Schur",

J. Combin. Teoría Ser. A , 112 (1): 44–81, doi : 10.1016 / j.jcta.2005.01.003 , S2CID 161241${\ Displaystyle k + 1}$${\ Displaystyle k}$ 

Lewis, Joel Brewster (2020), "Una nota sobre la acción de Hurwitz sobre factorizaciones de reflexión de elementos de Coxeter en grupos de reflexión complejos", Electron. J. Combin. , 27 (2): P2.54, arXiv : 2001.08238 , doi : 10.37236 / 9351

Lewis, Joel Brewster; McCammond, Jon; Petersen, T. Kyle; Schwer, Petra (2019), "Calcular la longitud de la reflexión en un grupo afín de Coxeter", Trans. Amer. Matemáticas. Soc. , 371 (6): 4097–4127, doi : 10.1090 / tran / 7472

Petersen, T.Kyle (2015), Números eulerianos , Textos avanzados Birkhäuser Basler Lehrbücher, Birkhauser, doi : 10.1007 / 978-1-4939-3091-3 , ISBN 978-1-4939-3090-6

Polster, Burkard (2003), Las matemáticas del malabarismo , Springer, ISBN 0-387-95513-5

Reiner, Victor (1995), "La distribución de descensos y longitud en un grupo Coxeter", Electron. J. Combin. , 2 : R25, doi : 10.37236 / 1219

Shephard, GC ; Todd, JA (1954), "Grupos de reflexión unitarios finitos", Canad. J. Math. , 6 : 274–304, doi : 10.4153 / CJM-1954-028-3

Shi, Jian-Yi (1986), células Kazhdan-Lusztig de ciertos grupos Weyl afines , Lecture Notes in Mathematics, 1179 , Springer, ISBN 3-540-16439-1

Shi, Jian-Yi (1991), "El algoritmo generalizado de Robinson-Schensted en el grupo afín de Weyl de tipo A _{n −1} ", J. Algebra , 139 (2): 364–394, CiteSeerX  10.1.1.551.3094 , doi : 10.1016 / 0021-8693 (91) 90300-W

Shi, Jian-Yi (2002), "Ciertos grupos de reflexión imprimitiva y sus versiones genéricas", Trans. Amer. Matemáticas. Soc. , 354 (5): 2115–2129, doi : 10.1090 / S0002-9947-02-02941-0

Stembridge, John (1996), "Sobre los elementos totalmente conmutativos de los grupos Coxeter", J. Algebr. Peine. , 5 (4): 353–385, doi : 10.1007 / BF00193185

Viennot, G. (1977), "Une forme géométrique de la correspondance de Robinson-Schensted", en Foata, Dominique (ed.), Combinatoire et représentation du groupe symétrique , Lecture Notes in Mathematics, 579 , Springer, págs. 29– 58, doi : 10.1007 / BFb0090011 , ISBN 978-3-540-08143-2