Racional diádico - Dyadic rational

Racionales diádicos en el intervalo de 0 a 1

En matemáticas, un racional diádico o racional binario es un número que se puede expresar como una fracción cuyo denominador es una potencia de dos . Por ejemplo, 1/2, 3/2 y 3/8 son racionales diádicos, pero 1/3 no lo es. Estos números son importantes en informática porque son los únicos con representaciones binarias finitas . Los racionales diádicos también tienen aplicaciones en pesos y medidas, firmas de compás musicales y educación matemática temprana. Pueden aproximarse con precisión a cualquier número real .

La suma, diferencia o producto de dos números racionales diádicos cualesquiera es otro número racional diádico, dado por una fórmula simple. Sin embargo, la división de un número racional diádico por otro no siempre produce un resultado racional diádico. Matemáticamente, esto significa que los números racionales diádicos forman un anillo , que se encuentra entre el anillo de los números enteros y el campo de los números racionales . Este anillo se puede denotar . ${\ Displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}]}$

En matemáticas avanzadas, los números racionales diádicas son fundamentales para las construcciones de la electroválvula diádico , la función de signo de interrogación de Minkowski , Daubechies ondas , grupo de Thompson , Prüfer-2 grupos , números surreales , y los números de fusibles . Estos números son orden-isomorfos a los números racionales; forman un subsistema de números 2-ádicos así como de los reales, y pueden representar las partes fraccionarias de números 2-ádicos. Se han utilizado funciones desde números naturales hasta racionales diádicos para formalizar el análisis matemático en matemáticas inversas .

Aplicaciones

En la medida

Pesas de cocina que miden fracciones diádicas de una libra desde 2 lb hasta 1/64 lb (1/4 oz)

Muchos sistemas tradicionales de pesos y medidas se basan en la idea de dividir a la mitad repetidamente, lo que produce racionales diádicos al medir cantidades fraccionarias de unidades. La pulgada se subdivide habitualmente en racionales diádicos en lugar de utilizar una subdivisión decimal. Las divisiones habituales del galón en medio galón, cuarto de galón , pintas y tazas también son diádicas. Los antiguos egipcios usaban racionales diádicos en la medición, con denominadores de hasta 64. De manera similar, los sistemas de pesos de la civilización del valle del Indo se basan en su mayor parte en reducciones a la mitad repetidas; antropóloga Heather M.-L. Miller escribe que "la reducción a la mitad es una operación relativamente simple con balances de vigas, que es probablemente la razón por la que tantos sistemas de peso de este período de tiempo usaban sistemas binarios".

En informática

Los racionales diádicos son fundamentales para la informática como un tipo de número fraccionario que muchas computadoras pueden manipular directamente. En particular, como tipo de datos utilizado por las computadoras, los números de punto flotante a menudo se definen como números enteros multiplicados por potencias positivas o negativas de dos. Los números que se pueden representar con precisión en un formato de punto flotante, como los tipos de datos de punto flotante IEEE , se denominan números representables. Para la mayoría de las representaciones de punto flotante, los números representables son un subconjunto de los racionales diádicos. Lo mismo ocurre con los tipos de datos de punto fijo , que también utilizan poderes de dos implícitamente en la mayoría de los casos. Debido a la simplicidad de la computación con racionales diádicos, también se utilizan para la computación real exacta usando aritmética de intervalos , y son fundamentales para algunos modelos teóricos de números computables .

La generación de una variable aleatoria a partir de bits aleatorios, en un período de tiempo fijo, solo es posible cuando la variable tiene un número finito de resultados cuyas probabilidades son todos números racionales diádicos. Para las variables aleatorias cuyas probabilidades no son diádicas, es necesario aproximar sus probabilidades mediante racionales diádicas o utilizar un proceso de generación aleatoria cuyo tiempo sea en sí mismo aleatorio e ilimitado.

En musica

Cinco barras de Igor Stravinski 's La consagración de la primavera
mostrando los compases³
₁₆, ²
₁₆, ³
₁₆, y ²
₈

Las firmas de tiempo en la notación musical occidental se escriben tradicionalmente en una forma que se asemeja a las fracciones (por ejemplo:²
₂, ⁴
₄, o ⁶
₈), aunque la línea horizontal del pentagrama musical que separa el número superior e inferior suele omitirse cuando se escribe la firma por separado de su pentagrama. Como fracciones, generalmente son diádicas, aunque también se han utilizado firmas de tiempo no diádicas . El valor numérico de la firma, interpretado como una fracción, describe la longitud de un compás como una fracción de una nota entera . Su numerador describe el número de tiempos por compás y el denominador describe la duración de cada tiempo.

En educación matemática

En las teorías del desarrollo infantil del concepto de fracción basadas en el trabajo de Jean Piaget , los números fraccionarios que surgen de la reducción a la mitad y la reducción repetida a la mitad se encuentran entre las primeras formas de fracciones en desarrollarse. Esta etapa de desarrollo del concepto de fracciones se ha denominado "reducción a la mitad algorítmica". La suma y resta de estos números se puede realizar en pasos que solo implican duplicar, dividir por la mitad, sumar y restar números enteros. Por el contrario, la suma y resta de fracciones más generales implica la multiplicación y factorización de números enteros para alcanzar un denominador común. Por lo tanto, las fracciones diádicas pueden ser más fáciles de calcular para los estudiantes que las fracciones más generales.

Definiciones y aritmética

Los números diádicos son los números racionales que resultan de dividir un número entero por una potencia de dos . Un número racional en términos más simples es un racional diádico cuando es una potencia de dos. Otra forma equivalente de definir los racionales diádicos es que son los números reales que tienen una representación binaria de terminación . ${\ Displaystyle p / q}$${\ Displaystyle q}$

La suma , resta y multiplicación de dos racionales diádicos cualesquiera produce otro racional diádico, de acuerdo con las siguientes fórmulas:

${\ Displaystyle {\ begin {alineado} {\ frac {a} {2 ^ {b}}} + {\ frac {c} {2 ^ {d}}} & = {\ frac {2 ^ {d- \ min (b, d)} a + 2 ^ {b- \ min (b, d)} c} {2 ^ {\ max (b, d)}}} \\ [6px] {\ frac {a} { 2 ^ {b}}} - {\ frac {c} {2 ^ {d}}} & = {\ frac {2 ^ {d- \ min (b, d)} a-2 ^ {b- \ min (b, d)} c} {2 ^ {\ max (b, d)}}} \\ [6px] {\ frac {a} {2 ^ {b}}} \ cdot {\ frac {c} { 2 ^ {d}}} & = {\ frac {ac} {2 ^ {b + d}}} \ end {alineado}}}$

Sin embargo, el resultado de dividir un racional diádico por otro no es necesariamente un racional diádico. Por ejemplo, 1 y 3 son números racionales diádicos, pero 1/3 no lo es.

Propiedades adicionales

Aproximaciones racionales diádicas a la raíz cuadrada de 2 ( ), que se obtienen redondeando al múltiplo entero más pequeño más cercano de para La altura de la región rosa por encima de cada aproximación es su error.${\ Displaystyle {\ sqrt {2}} \ approx 1.4142}$${\ Displaystyle 1/2 ^ {i}}$${\ Displaystyle i = 0,1,2, \ puntos}$

Números reales sin aproximaciones racionales diádicas inusualmente precisas. Los círculos rojos rodean los números que se aproximan dentro del error por . Para los números en el conjunto fractal de Cantor fuera de los círculos, todas las aproximaciones racionales diádicas tienen errores mayores.${\ displaystyle {\ tfrac {1} {6}} / 2 ^ {i}}$${\ Displaystyle n / 2 ^ {i}}$

Todo entero y todo medio entero es un racional diádico. Ambos cumplen con la definición de ser un número entero dividido por una potencia de dos: cada número entero es un número entero dividido por uno (la potencia cero de dos), y cada medio entero es un número entero dividido por dos.

Cada número real puede aproximarse de manera arbitraria y cercana mediante racionales diádicos. En particular, para un número real , considere los racionales diádicos de la forma , donde puede ser cualquier número entero y denota la función de piso que redondea su argumento a un número entero. Estos números se aproximan desde abajo hasta dentro de un error de , que puede hacerse arbitrariamente pequeño eligiendo ser arbitrariamente grande. Para un subconjunto fractal de los números reales, este límite de error está dentro de un factor constante de óptimo: para estos números, no existe una aproximación con un error menor que una constante . La existencia de aproximaciones diádicas precisas se puede expresar diciendo que el conjunto de todos los racionales diádicos es un denso en la línea real . Más fuertemente, este conjunto es uniformemente denso, en el sentido de que los racionales diádicos con denominador están uniformemente espaciados en la línea real. ${\ Displaystyle x}$${\ textstyle \ lfloor 2 ^ {i} x \ rfloor / 2 ^ {i}}$${\ Displaystyle i}$${\ Displaystyle \ lfloor \ dots \ rfloor}$${\ Displaystyle x}$${\ Displaystyle 1/2 ^ {i}}$${\ Displaystyle i}$${\ Displaystyle n / 2 ^ {i}}$${\ Displaystyle 1/2 ^ {i}}$${\ Displaystyle 2 ^ {i}}$

Los racionales diádicos son precisamente aquellos números que poseen expansiones binarias finitas . Sus expansiones binarias no son únicas; hay una representación finita y una infinita de cada racional diádico diferente de 0 (ignorando los ceros terminales). Por ejemplo, 0.11 ₂ = 0.10111 ... ₂ , dando dos representaciones diferentes para 3/4. Los racionales diádicos son los únicos números cuyas expansiones binarias no son únicas.

En matemáticas avanzadas

Estructura algebraica

Debido a que están cerrados bajo suma, resta y multiplicación, pero no división, los racionales diádicos son un anillo pero no un campo . El anillo de los racionales diádicos se puede denotar , lo que significa que se puede generar evaluando polinomios con coeficientes enteros, en el argumento 1/2. Como anillo, los racionales diádicos son un subanillo de los números racionales y un subanillo de los enteros. Algebraicamente, este anillo es la localización de los enteros con respecto al conjunto de potencias de dos . ${\ Displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}]}$

Además de formar un subanillo de los números reales , los números racionales diádicos forman un subanillo de los números 2-ádicos , un sistema de números que se puede definir a partir de representaciones binarias que son finitas a la derecha del punto binario pero que pueden extenderse infinitamente. muy a la izquierda. Los números 2-ádicos incluyen todos los números racionales, no solo los racionales diádicos. Incrustar los racionales diádicos en los números 2-ádicos no cambia la aritmética de los racionales diádicos, pero les da una estructura topológica diferente a la que tienen como subanillo de los números reales. Como lo hacen en los reales, los racionales diádicos forman un subconjunto denso de los números 2-ádicos, y son el conjunto de números 2-ádicos con expansiones binarias finitas. Cada número 2-ádico se puede descomponer en la suma de un número entero 2-ádico y un racional diádico; en este sentido, los racionales diádicos pueden representar las partes fraccionarias de números 2-ádicos, pero esta descomposición no es única.

La suma de los racionales diádicos módulo 1 (el grupo cociente de los racionales diádicos por los números enteros) forma el grupo 2 de Prüfer . ${\ Displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}] / \ mathbb {Z}}$

Solenoide diádico

Considerar solo las operaciones de suma y resta de los racionales diádicos les da la estructura de un grupo abeliano aditivo . La dualidad de Pontryagin es un método para comprender los grupos abelianos mediante la construcción de grupos duales, cuyos elementos son caracteres del grupo original, homomorfismos de grupo al grupo multiplicativo de los números complejos , con la multiplicación puntual como la operación de grupo dual. El grupo dual de los racionales diádicos aditivos, así construido, también puede verse como un grupo topológico . Se llama solenoide diádico y es isomorfo al producto topológico de los números reales y los números 2-ádicos, coorientado por la inserción diagonal de los racionales diádicos en este producto. Es un ejemplo de un protorus , un solenoide y un continuo indecomponible .

Funciones con racionales diádicos como puntos distinguidos

La función de signo de interrogación de Minkowski asigna números racionales a racionales diádicos

A Daubechies Wavelet , mostrando puntos de no-uniformidad en racionales diádicas

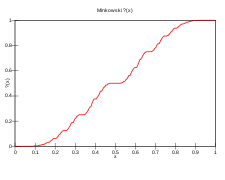
Debido a que son un subconjunto denso de los números reales, los racionales diádicos, con su orden numérico, forman un orden denso . Al igual que con dos órdenes lineales densos contables ilimitados, según el teorema de isomorfismo de Cantor , los racionales diádicos son orden-isomorfos a los números racionales. En este caso, la función del signo de interrogación de Minkowski proporciona una biyección que preserva el orden entre el conjunto de todos los números racionales y el conjunto de los racionales diádicos.

Los racionales diádicos juegan un papel clave en el análisis de las ondas de Daubechies , como el conjunto de puntos donde la función de escala de estas ondas no es uniforme. De manera similar, los racionales diádicos parametrizan las discontinuidades en el límite entre puntos estables e inestables en el espacio de parámetros del mapa de Hénon .

El conjunto de homeomorfismos lineales por partes desde el intervalo unitario hasta sí mismo que tienen pendientes de potencia de 2 y puntos de corte diádico-racionales forma un grupo bajo la operación de composición de funciones . Este es el grupo de Thompson , el primer ejemplo conocido de un grupo simple infinito pero presentado de manera finita . El mismo grupo también puede ser representado por una acción sobre árboles binarios enraizados, o por una acción sobre los racionales diádicos dentro del intervalo unitario.

Otras construcciones relacionadas

En matemáticas inversas , una forma de construir los números reales es representarlos como funciones de números unarios a racionales diádicos, donde el valor de una de estas funciones para el argumento es un racional diádico con denominador que se aproxima al número real dado. Definir números reales de esta manera permite probar muchos de los resultados básicos del análisis matemático dentro de una teoría restringida de aritmética de segundo orden llamada "análisis factible" (BTFA). ${\ Displaystyle i}$${\ Displaystyle 2 ^ {i}}$

Los números surrealistas son generados por un principio de construcción iterado que comienza generando todos los racionales diádicos finitos, y luego continúa creando nuevos y extraños tipos de infinitos, infinitesimales y otros números. Este sistema numérico es fundamental para la teoría de juegos combinatorios , y los racionales diádicos surgen naturalmente en esta teoría como el conjunto de valores de ciertos juegos combinatorios.

Los números fusibles son un subconjunto de los racionales diádicos, el cierre del conjunto bajo la operación , restringido a pares con . Están bien ordenados , con un tipo de orden igual al número épsilon . Para cada entero, el número fusible más pequeño que es mayor que tiene la forma . La existencia de para cada uno no se puede probar en la aritmética de Peano , y crece tan rápidamente en función de eso porque (en la notación de flecha hacia arriba de Knuth para números grandes) ya es mayor que . ${\ Displaystyle \ {0 \}}$${\ displaystyle x, y \ mapsto (x + y + 1) / 2}$${\ Displaystyle x, y}$${\ Displaystyle | xy | <1}$ ${\ Displaystyle \ varepsilon _ {0}}$${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle n + 1/2 ^ {k}}$${\ Displaystyle k}$${\ Displaystyle n}$${\ Displaystyle k}$${\ Displaystyle n}$${\ Displaystyle n = 3}$${\ Displaystyle 2 \ uparrow ^ {9} 16}$

Referencias