Sintaxis y símbolos de APL - APL syntax and symbols
El lenguaje de programación APL se distingue por ser simbólico en lugar de léxico : sus primitivas se indican mediante símbolos , no palabras. Estos símbolos se diseñaron originalmente como una notación matemática para describir algoritmos. Los programadores de APL a menudo asignan nombres informales cuando discuten funciones y operadores (por ejemplo, producto para × /), pero las funciones centrales y los operadores proporcionados por el lenguaje se indican mediante símbolos no textuales.
Funciones monádicas y diádicas
La mayoría de los símbolos denotan funciones u operadores . Una función monádica toma como argumento el resultado de evaluar todo a su derecha. (Moderado de la forma habitual entre paréntesis.) Una función diádica tiene otro argumento, el primer elemento de datos a su izquierda. Muchos símbolos denotan funciones tanto monádicas como diádicas, interpretadas según el uso. Por ejemplo, ⌊3.2 da 3, el número entero más grande que no está por encima del argumento, y 3⌊2 da 2, el menor de los dos argumentos.
Funciones y operadores
APL usa el término operador en el sentido de Heaviside como moderador de una función en oposición al uso de algún otro lenguaje de programación del mismo término como algo que opera sobre datos, ref. operador relacional y operadores en general . Otros lenguajes de programación a veces también usan este término de manera intercambiable con función , sin embargo, ambos términos se usan en APL de manera más precisa. Las primeras definiciones de los símbolos APL eran muy específicas sobre cómo se categorizaban los símbolos. Por ejemplo, el operador reduce se indica con una barra inclinada y reduce una matriz a lo largo de un eje interponiendo su función operando . Un ejemplo de reducir :
×/2 3 4 24 |
<< Resultados equivalentes en APL >> << Reducir operador / usado a la izquierda |
2×3×4 24 |
En el caso anterior, el operador de reducción o barra modera la función de multiplicación . La expresión × / 2 3 4 se evalúa como un resultado escalar (solo 1 elemento) mediante la reducción de una matriz por multiplicación. El caso anterior está simplificado, imagina multiplicar (sumar, restar o dividir) más que unos pocos números juntos. (A partir de un vector, × / devuelve el producto de todos sus elementos).
1 0 1\45 67 45 0 67 |
<< Resultados opuestos en APL >> << Expandir la función diádica \ usada a la izquierda Replicar la función diádica / usada a la derecha >> |
1 0 1/45 0 67 45 67 |
Los ejemplos de funciones diádicas anteriores [ejemplos de izquierda y derecha] (usando el mismo símbolo / , ejemplo de la derecha) demuestran cómo los valores booleanos (0 y 1) pueden usarse como argumentos izquierdos para las funciones \ expandir y / replicar para producir resultados exactamente opuestos. En el lado izquierdo, el vector de 2 elementos {45 67} se expande donde ocurren los 0 booleanos para dar como resultado un vector de 3 elementos {45 0 67}; observe cómo APL insertó un 0 en el vector. Por el contrario, ocurre exactamente lo contrario en el lado derecho, donde un vector de 3 elementos se convierte en solo 2 elementos; 0s booleanos eliminan elementos usando la función dyadic / slash . Los símbolos APL también operan en listas (vector) de elementos que utilizan tipos de datos distintos a los numéricos, por ejemplo, un vector de 2 elementos de cadenas de caracteres {"Apples" "Oranges"} podría sustituirse por el vector numérico {45 67} anterior.
Reglas de sintaxis
En APL no existe una jerarquía de precedencia para funciones u operadores. APL no sigue la precedencia de operador habitual de otros lenguajes de programación; por ejemplo, ×no vincula sus operandos más "estrechamente" que +. En lugar de la precedencia del operador, APL define una noción de alcance .
El alcance de una función determina sus argumentos . Las funciones tienen un alcance derecho largo : es decir, toman como argumentos correctos todo lo que está a su derecha. Una función diádica tiene un alcance izquierdo corto : toma como argumentos de la izquierda el primer dato a su izquierda. Por ejemplo, (la columna más a la izquierda a continuación es el código de programa real de una sesión de usuario de APL , sangrado = entrada real del usuario , sin sangría = resultado devuelto por el intérprete de APL ):
1 ÷ 2 ⌊ 3 × 4 - 5
¯0.3333333333
1 ÷ 2 ⌊ 3 × ¯1
¯0.3333333333
1 ÷ 2 ⌊ ¯3
¯0.3333333333
1 ÷ ¯3
¯0.3333333333
|
<< Primera nota: no hay paréntesis y Paso 2) 3 veces -1 = -3. |
Un operador puede tener operandos de función o datos y evaluar una función diádica o monádica. Los operadores tienen un largo alcance izquierdo. Un operador toma como su operando izquierdo la función más larga a su izquierda. Por ejemplo:
∘.=/⍳¨3 3 1 0 0 0 1 0 0 0 1
|
Subanálisis atómico o fragmentado de APL ( explicación completa ): La diéresis ¨ o mini punto doble significa repetir o sobre cada uno o realizar cada uno por separado para que se repita iota (en términos humanos, es decir, al revés, el intérprete de APL lee 3 3 sobre cada iota de uso), de manera concisa: iota para cada 3 . |
El operando izquierdo para el operador over-each¨ es la función índice.. La función derivada ⍳¨ se usa monádicamente y toma como su operando derecho el vector 3 3. El alcance izquierdo de cada uno es terminado por el operador de reducción , denotado por la barra diagonal . Su operando izquierdo es la expresión de función a su izquierda: el producto externo de la función igual . El resultado de ∘. = / Es una función monádica. Con el alcance derecho largo habitual de una función, toma como argumento derecho el resultado de ⍳¨3 3. Así
(⍳3)(⍳3)
1 2 3 1 2 3
(⍳3)∘.=⍳3
1 0 0
0 1 0
0 0 1
⍳¨3 3
1 2 3 1 2 3
∘.=/⍳¨3 3
1 0 0
0 1 0
0 0 1
|
La matriz de unos y ceros producida de forma similar por Las matrices de identidad son útiles para resolver determinantes de matrices , grupos de ecuaciones lineales y regresión múltiple . |
im ← ∘.=⍨∘⍳
im 3
1 0 0
0 1 0
0 0 1
|
Algunos intérpretes APL apoyan el componer operador ∘ y el viaje operador ⍨ . El primero ∘ pega funciones juntas de modo que foo∘bar , por ejemplo, podría ser una función hipotética que aplica la función definida foo al resultado de la función definida bar ; foo y bar pueden representar cualquier función existente. En los casos en los que una función diádica se modera mediante conmutación y luego se usa de manera monádica, su argumento derecho se toma también como su argumento izquierdo. Por lo tanto, una función derivada o compuesta (llamada im a la izquierda) se usa en la sesión de usuario de APL para devolver una matriz de identidad de 9 elementos usando su argumento , parámetro u operando derecho = 3. |
Letters←"ABCDE"
Letters
ABCDE
⍴Letters
5
FindIt←"CABS"
FindIt
CABS
⍴FindIt
4
Letters ⍳ FindIt
3 1 2 6
|
Ejemplo de uso de APL para indexar ⍳ o buscar (o no encontrar) elementos en un vector de caracteres : Primero, a la variable Letters se le asigna un vector de 5 elementos, en este caso, letras del alfabeto. La forma ⍴ o la longitud del vector de caracteres de Letters es 5. FindIt variable se le asigna qué buscar en letras y su longitud es de 4 caracteres. 1 2 3 4 5 << posiciones vectoriales o números de índice en letras A la izquierda, la función diádica iota busca a través de su argumento izquierdo (Letras) la cadena de búsqueda (argumento derecho de iota, FindIt). Iota encuentra letra "C" en la posición 3 en Letras, se encuentra "A" en la posición 1, y "B" en la posición 2. Iota no no encontró letra "S" en cualquier lugar de la variable Letters, por lo que devuelve el número 6, que es 1 mayor que la longitud de Letters. Iota encontró letras "CABINA" (3 1 2). Iota no encontró correctamente "S" (6). |
Funciones monádicas
| Nombre (s) | Notación | Significado | Punto de código Unicode |
|---|---|---|---|
| Rodar |
?B
|
Un entero seleccionado al azar de los primeros B enteros | U + 003F ? |
| Techo |
⌈B
|
Mínimo entero mayor o igual que B | U + 2308 ⌈ |
| Suelo |
⌊B
|
Mayor número entero menor o igual que B | U + 230A ⌊ |
| Forma, Rho |
⍴B
|
Número de componentes en cada dimensión de B | U + 2374 ⍴ |
| No , Tilde |
∼B
|
Lógico: ∼1 es 0, ∼0 es 1 | U + 223C ∼ |
| Valor absoluto |
∣B
|
Magnitud de B | U + 2223 ∣ |
| Generador de índices, Iota |
⍳B
|
Vector de los primeros B enteros | U + 2373 ⍳ |
| Exponencial |
⋆B
|
e a la potencia B | U + 22C6 ⋆ |
| Negación |
−B
|
Cambia el signo de B | U + 2212 - |
| Conjugado |
+B
|
El conjugado complejo de B (los números reales se devuelven sin cambios) | U + 002B + |
| Signum |
×B
|
¯1 si B <0; 0 si B = 0; 1 si B > 0 | U + 00D7 × |
| Recíproco |
÷B
|
1 dividido por B | U + 00F7 ÷ |
| Ravel, Catenate, Laminado |
,B
|
Transforma B en un vector | U + 002C , |
| Matriz inversa , división cuádruple monádica |
⌹B
|
Inversa de la matriz B | U + 2339 ⌹ |
| Pi veces |
○B
|
Multiplicar por π | U + 25CB ○ |
| Logaritmo |
⍟B
|
Logaritmo natural de B | U + 235F ⍟ |
| Inversión |
⌽B
|
Invertir elementos de B a lo largo del último eje | U + 233D ⌽ |
| Inversión |
⊖B
|
Invertir elementos de B a lo largo del primer eje | U + 2296 ⊖ |
| Subir de nivel |
⍋B
|
Índices de B que ordenarán B en orden ascendente | U + 234B ⍋ |
| Degradar de categoría |
⍒B
|
Índices de B que ordenarán B en orden descendente | U + 2352 ⍒ |
| Ejecutar |
⍎B
|
Ejecuta una expresión APL | U + 234E ⍎ |
| Formato monádico |
⍕B
|
Una representación de carácter de B | U + 2355 ⍕ |
| Transposición monádica |
⍉B
|
Invertir los ejes de B | U + 2349 ⍉ |
| Factorial |
!B
|
Producto de enteros 1 a B | U + 0021 ! |
Funciones diádicas
| Nombre (s) | Notación | Significado | Punto de código Unicode |
|---|---|---|---|
| Agregar |
A+B
|
Suma de A y B | U + 002B + |
| Sustraer |
A−B
|
A menos B | U + 2212 - |
| Multiplicar |
A×B
|
A multiplicado por B | U + 00D7 × |
| Dividir |
A÷B
|
A dividido por B | U + 00F7 ÷ |
| Exponenciación |
A⋆B
|
A elevado a la potencia B | U + 22C6 ⋆ |
| Circulo |
A○B
|
Funciones trigonométricas de B seleccionadas por A
A=1: sin(B) A=5: sinh(B) A=2: cos(B) A=6: cosh(B) A=3: tan(B) A=7: tanh(B) Los negativos producen la inversa de las funciones respectivas |
U + 25CB ○ |
| Negociar |
A?B
|
A enteros distintos seleccionados al azar de los primeros B enteros | U + 003F ? |
| Membresía, Epsilon |
A∈B
|
1 para elementos de A presentes en B ; 0 donde no. | U + 2208 ∈ |
| Find, Epsilon Underbar |
A⍷B
|
1 para el punto de partida de la matriz A de varios elementos presente en B ; 0 donde no. | U + 2377 ⍷ |
| Máximo , techo |
A⌈B
|
El mayor valor de A o B | U + 2308 ⌈ |
| Mínimo , Piso |
A⌊B
|
El valor más pequeño de A o B | U + 230A ⌊ |
| Remodelación, Dyadic Rho |
A⍴B
|
Matriz de forma A con datos B | U + 2374 ⍴ |
| Llevar |
A↑B
|
Seleccione el primer (o último) elemento A de B según × A | U + 2191 ↑ |
| Soltar |
A↓B
|
Eliminar el primer (o último) elemento A de B de acuerdo con × A | U + 2193 ↓ |
| Descodificar |
A⊥B
|
Valor de un polinomio cuyos coeficientes son B en A | U + 22A5 ⊥ |
| Codificar |
A⊤B
|
Base: una representación del valor de B | U + 22A4 ⊤ |
| Residuo |
A∣B
|
B módulo A | U + 2223 ∣ |
| Cadena |
A,B
|
Elementos de B añadidos a los elementos de A | U + 002C , |
| Expansión, barra invertida diádica |
A\B
|
Inserte ceros (o espacios en blanco) en B correspondientes a ceros en A | U + 005C \ |
| Compresión, barra diádica |
A/B
|
Seleccione los elementos en B correspondientes a los de A | U + 002F / |
| Índice de, Dyadic Iota |
A⍳B
|
La ubicación (índice) de B en A ; si no se encuentra
1+⍴A |
U + 2373 ⍳ |
| División de matriz, división cuádruple diádica |
A⌹B
|
Solución al sistema de ecuaciones lineales , regresión múltiple A x = B | U + 2339 ⌹ |
| Rotación |
A⌽B
|
Los elementos de B se rotan en posiciones A | U + 233D ⌽ |
| Rotación |
A⊖B
|
Los elementos de B se rotan en posiciones A a lo largo del primer eje | U + 2296 ⊖ |
| Logaritmo |
A⍟B
|
Logaritmo de B en base A | U + 235F ⍟ |
| Formato diádico |
A⍕B
|
Formatee B en una matriz de caracteres de acuerdo con A | U + 2355 ⍕ |
| Transposición general |
A⍉B
|
Los ejes de B están ordenados por A | U + 2349 ⍉ |
| Combinaciones |
A!B
|
Número de combinaciones de B tomadas A a la vez | U + 0021 ! |
| Diéresis, Dieresis, Doble punto |
A¨B
|
Sobre cada uno, o realizar cada uno por separado; B = en estos; A = operación a realizar o usar (p. Ej., Iota) | U + 00A8 ¨ |
| Menos que |
A < B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 003C < |
| Menor o igual |
A≤B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 2264 ≤ |
| Igual |
A=B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 003D = |
| Mayor que o igual |
A≥B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 2265 ≥ |
| Mas grande que |
A>B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 003E > |
| No es igual |
A≠B
|
Comparación: 1 si es verdadero, 0 si es falso | U + 2260 ≠ |
| O |
A∨B
|
Lógica booleana: 0 (falso) si tanto A como B = 0 , 1 en caso contrario. Alt: 1 (verdadero) si A o B = 1 (verdadero) | U + 2228 ∨ |
| Y |
A∧B
|
Lógica booleana: 1 (verdadero) si tanto A como B = 1 , 0 (falso) en caso contrario | U + 2227 ∧ |
| Ni |
A⍱B
|
Lógica booleana: 1 si tanto A como B son 0, de lo contrario 0. Alt: ~ ∨ = no O | U + 2371 ⍱ |
| Nand |
A⍲B
|
Lógica booleana: 0 si tanto A como B son 1, de lo contrario 1. Alt: ~ ∧ = no Y | U + 2372 ⍲ |
| Izquierda |
A⊣B
|
A | U + 22A3 ⊣ |
| Derecha |
A⊢B
|
B | U + 22A2 ⊢ |
Operadores e indicador de ejes
| Nombre (s) | Símbolo | Ejemplo | Significado (de ejemplo) | Secuencia de puntos de código Unicode |
|---|---|---|---|---|
| Reducir (último eje), barra | / |
+/B
|
Suma en B | U + 002F / |
| Reducir (primer eje) | ⌿ |
+⌿B
|
Suma B | U + 233F ⌿ |
| Escaneo (último eje), barra invertida | \ |
+\B
|
Suma corriente a través de B | U + 005C \ |
| Escaneo (primer eje) | ⍀ |
+⍀B
|
Corriendo suma hacia abajo B | U + 2340 ⍀ |
| Producto Interno | . |
A+.×B
|
Producto matricial de A y B | U + 002E . |
| Producto exterior | ∘. |
A∘.×B
|
Producto externo de A y B | U + 2218 ∘ , U + 002E . |
Notas: Los operadores de reducción y exploración esperan una función diádica a su izquierda, formando una función compuesta monádica aplicada al vector de su derecha.
El operador de producto "." espera una función diádica tanto a su izquierda como a su derecha, formando una función compuesta diádica aplicada a los vectores de su izquierda y derecha. Si la función a la izquierda del punto es "∘" (que significa nulo), entonces la función compuesta es un producto externo; de lo contrario, es un producto interno. Un producto interno destinado a la multiplicación de matrices convencional usa las funciones + y ×, reemplazándolas con otras funciones diádicas puede resultar en operaciones alternativas útiles.
Algunas funciones pueden ir seguidas de un indicador de eje entre corchetes (cuadrados), es decir, aparece entre una función y una matriz y no debe confundirse con subíndices de matriz escritos después de una matriz. Por ejemplo, dada la función ⌽ (inversión) y una matriz bidimensional, la función opera por defecto a lo largo del último eje, pero esto se puede cambiar usando un indicador de eje:
A←4 3⍴⍳12
A
1 2 3
4 5 6
7 8 9
10 11 12
⌽A
3 2 1
6 5 4
9 8 7
12 11 10
⌽[1]A
10 11 12
7 8 9
4 5 6
1 2 3
⊖⌽A
12 11 10
9 8 7
6 5 4
3 2 1
⍉A
1 4 7 10
2 5 8 11
3 6 9 12
|
A ahora se refleja o se invierte a lo largo de su eje vertical como indica visualmente el símbolo ⌽ . A ahora se refleja utilizando el indicador de eje [1] o el modificador de primera dimensión . El resultado es que la variable A se ha reflejado en el eje horizontal, en lugar de verticalmente. A ahora se refleja tanto verticalmente ⊖ como horizontalmente ⌽ . A se transpone ⍉ a una matriz de 3 filas por 4 columnas, de modo que las filas y columnas se intercambian, como el símbolo ⍉ representa visualmente. Compare el resultado aquí con la matriz original almacenada en A, la matriz superior. Estos tipos de transformaciones de datos son útiles en el análisis de series de tiempo y coordenadas espaciales , solo dos ejemplos, existen más . |
Como caso particular, si la función "," de catenados diádicos va seguida de un indicador de eje (o un modificador de eje a un símbolo / función), se puede utilizar para laminar (interponer) dos matrices dependiendo de si el indicador de eje es menor que o mayor que el origen del índice (origen del índice = 1 en la ilustración siguiente):
B←1 2 3 4
C←5 6 7 8
B,C
1 2 3 4 5 6 7 8
B,[0.5]C
1 2 3 4
5 6 7 8
B,[1.5]C
1 5
2 6
3 7
4 8
|
A la izquierda, a la variable 'B' se le asigna primero un vector de 4 números enteros consecutivos (por ejemplo, ⍳4 ). |
Matrices anidadas
Las matrices son estructuras que tienen elementos agrupados linealmente como vectores o en forma de tabla como matrices , y dimensiones más altas (3D o al cubo, 4D o al cubo a lo largo del tiempo , etc.). Las matrices que contienen tanto caracteres como números se denominan matrices mixtas . Las estructuras de matriz que contienen elementos que también son matrices se denominan matrices anidadas .
| Sesión de usuario con intérprete de APL | Explicación |
|---|---|
X←4 5⍴⍳20
X
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
X[2;2]
7
⎕IO
1
X[1;1]
1
|
El elemento X [2; 2] en la fila 2 - la columna 2 actualmente es un número entero = 7 . Origen del índice inicial Valor ⎕IO = 1 . Por tanto, el primer elemento de la matriz X o X [1; 1] = 1 . |
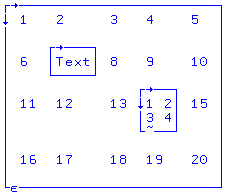
X[2;2]←⊂"Text"
X[3;4]←⊂(2 2⍴⍳4)
X
1 2 3 4 5
6 Text 8 9 10
11 12 13 1 2 15
3 4
16 17 18 19 20
|
Elemento en X [fila 2; col 2] se cambia (de 7) a un vector anidado "Texto" usando la función enclose ⊂ . Elemento en X [fila 3; col 4], antes entero 14, ahora se convierte en una matriz 2x2 mini encerrada o anidada 4 de 4 enteros consecutivos. Dado que X contiene números , texto y elementos anidados , es una matriz mixta y anidada . |
Control de flujo
Un usuario puede definir funciones personalizadas que, al igual que las variables, se identifican por su nombre en lugar de por un símbolo no textual. El encabezado de la función define si una función personalizada es niladica (sin argumentos), monádica (un argumento a la derecha) o diádica (argumentos a la izquierda y a la derecha), el nombre local del resultado (a la izquierda de la flecha ← asignar ) y si tiene cualquier variable local (cada una separada por punto y coma ';').
| Función niladica PI o π (pi) | Función monádica CIRCLEAREA | Función diádica SEGMENTAREA, con variables locales |
|---|---|---|
∇ RESULT←PI
RESULT←○1
∇
|
∇ AREA←CIRCLEAREA RADIUS
AREA←PI×RADIUS⋆2
∇
|
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS
AREA←FRACTION×CA
∇
|
Si las funciones con el mismo identificador pero diferente adicción son distintas está definido por la implementación. Si se permite, entonces una función CURVEAREA podría definirse dos veces para reemplazar tanto la CIRCLEAREA monádica como la SEGMENTAREA diádica anterior, con la función monádica o diádica seleccionada por el contexto en el que se hizo referencia.
Las funciones diádicas personalizadas generalmente se pueden aplicar a parámetros con las mismas convenciones que las funciones integradas, es decir, los arreglos deben tener el mismo número de elementos o uno de ellos debe tener un solo elemento extendido. Hay excepciones a esto, por ejemplo, una función para convertir moneda británica pre-decimal a dólares esperaría tomar un parámetro con exactamente tres elementos que representan libras, chelines y peniques.
Dentro de un programa o una función personalizada, el control puede transferirse condicionalmente a una declaración identificada por un número de línea o una etiqueta explícita; si el objetivo es 0 (cero), esto finaliza el programa o vuelve al llamador de una función. La forma más común usa la función de compresión APL, como en la plantilla (condición) / objetivo que tiene el efecto de evaluar la condición en 0 (falso) o 1 (verdadero) y luego usarla para enmascarar el objetivo (si la condición es falso se ignora, si es verdadero se deja solo para que se transfiera el control).
Por lo tanto, la función SEGMENTAREA puede modificarse para abortar (justo debajo), devolviendo cero si los parámetros (DEGREES y RADIUS a continuación) tienen un signo diferente :
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN ⍝ local variables denoted by semicolon(;)
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS ⍝ this APL code statement calls user function CIRCLEAREA, defined up above.
SIGN←(×DEGREES)≠×RADIUS ⍝ << APL logic TEST/determine whether DEGREES and RADIUS do NOT (≠ used) have same SIGN 1-yes different(≠), 0-no(same sign)
AREA←0 ⍝ default value of AREA set = zero
→SIGN/0 ⍝ branching(here, exiting) occurs when SIGN=1 while SIGN=0 does NOT branch to 0. Branching to 0 exits function.
AREA←FRACTION×CA
∇
La función anterior SEGMENTAREA funciona como se esperaba si los parámetros son escalares o matrices de un solo elemento , pero no si son matrices de elementos múltiples, ya que la condición termina basándose en un solo elemento de la matriz SIGN; por otro lado, el usuario La función podría modificarse para manejar correctamente los argumentos vectorizados. La operación a veces puede ser impredecible ya que APL define que las computadoras con capacidades de procesamiento de vectores deben paralelizar y pueden reordenar las operaciones de matriz en la medida de lo posible; por lo tanto, pruebe y depure funciones de usuario, particularmente si se usarán con argumentos vectoriales o incluso matriciales. Esto afecta no solo la aplicación explícita de una función personalizada a las matrices, sino también su uso en cualquier lugar donde una función diádica pueda usarse razonablemente, como en la generación de una tabla de resultados:
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0 0 0
0 0 0
0 0 0
0 0 0
Una forma más concisa y, a veces, mejor, de formular una función es evitar transferencias explícitas de control, en lugar de utilizar expresiones que evalúen correctamente en todas las condiciones o en las esperadas. A veces es correcto dejar que una función falle cuando uno o ambos argumentos de entrada son incorrectos , precisamente para que el usuario sepa que uno o ambos argumentos utilizados eran incorrectos. Lo siguiente es más conciso que la función SEGMENTAREA anterior. Lo siguiente es importante , maneja correctamente los argumentos vectorizados:
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS
SIGN←(×DEGREES)≠×RADIUS
AREA←FRACTION×CA×~SIGN ⍝ this APL statement is more complex, as a one-liner - but it solves vectorized arguments: a tradeoff - complexity vs. branching
∇
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0.785398163 0 12.5663706
1.57079633 0 25.1327412
2.35619449 0 37.6991118
0 ¯3.14159265 0
Evitar las transferencias explícitas de control también llamados ramificación, si no han sido revisados o cuidadosamente controlado - puede promover el uso de una excesiva complejidad forros uno , verdaderamente "mal entendido y expresiones complejas" y una "escritura exclusiva" estilo, que tiene poco hecho a APL querer por influyentes comentaristas como Edsger Dijkstra . Sin embargo, a la inversa, los modismos de APL pueden ser divertidos, educativos y útiles, si se usan con comentarios útiles ⍝ , por ejemplo, incluyendo la fuente y el significado y la función del idioma (s). Aquí hay una lista de modismos APL , una lista de modismos IBM APL2 aquí y una biblioteca de modismos APL finlandesa aquí .
Diverso
| Nombre (s) | Símbolo | Ejemplo | Significado (de ejemplo) | Punto de código Unicode |
|---|---|---|---|---|
| Alto menos | ¯ |
¯3
|
Denota un número negativo | U + 00AF ¯ |
| Lámpara, comentario | ⍝ |
⍝This is a comment
|
Todo a la derecha de ⍝ denota un comentario | U + 235D ⍝ |
| Flecha derecha, rama, ir a | → |
→This_Label
|
→ This_Label envía la ejecución de APL a This_Label: | U + 2192 → |
| Asignar, Flecha izquierda, Establecer en | ← |
B←A
|
B ← A establece los valores y la forma de B para que coincidan con A | U + 2190 ← |
La mayoría de las implementaciones de APL admiten una serie de variables y funciones del sistema, generalmente precedidas por el carácter ⎕ (quad) y o ")" ( gancho = cerrar paréntesis). Particularmente importante y ampliamente implementada es la variable ⎕IO ( Origen del índice ), ya que mientras que el IBM APL original basaba sus matrices en 1, algunas variantes más nuevas las basan en cero:
| Sesión de usuario con intérprete de APL | Descripción |
|---|---|
X←⍳12
X
1 2 3 4 5 6 7 8 9 10 11 12
⎕IO
1
X[1]
1
|
X conjunto = al vector de 12 enteros consecutivos. Origen del índice inicial Valor valueIO = 1 . Por lo tanto, la primera posición en el vector X o X [1] = 1 por vector de valores de iota { 1 2 3 4 5 ...}. |
⎕IO←0
X[1]
2
X[0]
1
|
Origen del índice ⎕IO ahora cambió a 0. Por lo tanto, la 'primera posición de índice' en el vector X cambia de 1 a 0. En consecuencia, X [1] luego hace referencia o apunta a 2 desde {1 2 3 4 5 ...} y X [0] ahora hace referencia a 1 . |
⎕WA
41226371072
|
Quad WA o ⎕WA , otra variable dinámica del sistema , muestra cuánta área de trabajo permanece sin usar o 41,226 megabytes o aproximadamente 41 gigabytes de área de trabajo libre total adicional sin usar disponible para que el espacio de trabajo APL y el programa lo procesen. Si este número es bajo o se acerca a cero, es posible que la computadora necesite más memoria de acceso aleatorio (RAM), espacio en el disco duro o alguna combinación de los dos para aumentar la memoria virtual . |
)VARS
X
|
) VARS una función del sistema en APL, ) VARS muestra los nombres de las variables de usuario existentes en el espacio de trabajo actual. |
También hay funciones del sistema disponibles para que los usuarios guarden el espacio de trabajo actual, por ejemplo, ) GUARDAR y finalizar el entorno APL, por ejemplo, ) APAGADO : a veces se denominan comandos o funciones de gancho debido al uso de un paréntesis o gancho derecho al principio. Existe cierta estandarización de estas funciones cuádruples y de gancho.
Fuentes
El plano multilingüe básico Unicode incluye los símbolos APL en el bloque Técnico misceláneo , que, por lo tanto, generalmente se representan con precisión a partir de las fuentes Unicode más grandes instaladas con la mayoría de los sistemas operativos modernos. Estas fuentes rara vez las diseñan tipógrafos familiarizados con los glifos APL. Por lo tanto, aunque son precisos, los glifos pueden parecer desconocidos para los programadores de APL o ser difíciles de distinguir entre sí.
Algunas fuentes Unicode se han diseñado para mostrar APL correctamente: APLX Upright, APL385 Unicode y SimPL.
Antes de Unicode, a los intérpretes APL se les proporcionaban fuentes en las que los caracteres APL se asignaban a posiciones menos utilizadas en los conjuntos de caracteres ASCII, generalmente en los 128 puntos de código superiores. Estas asignaciones (y sus variaciones nacionales) eran a veces exclusivas del intérprete de cada proveedor de APL, lo que hacía que la visualización de programas de APL en la Web, en archivos de texto y manuales, a menudo fuera problemática.
Función de teclado APL2 para mapeo de símbolos
Tenga en cuenta la tecla APL de encendido / apagado: la tecla más a la derecha, justo debajo. También tenga en cuenta el teclado tenía unos 55 únicas (68 enumeran por tablas anteriores, incluidos los símbolos comparativos pero varios símbolos aparecen en las dos teclas de símbolos APL tablas monádicos y diádicas) (funciones 55 APL (operadores) se enumeran en 5110 APL de referencia de IBM Manual), por lo tanto con el uso de las teclas alt, shift y ctrl - teóricamente habría permitido un máximo de 59 (teclas) * 4 (con 2 teclas presionadas) * 3 (con tres teclas presionadas, por ejemplo, ctrl-alt-del) o unas 472 combinaciones de teclas máximas diferentes, acercándose al máximo de 512 caracteres EBCDIC (256 caracteres por 2 códigos para cada combinación de teclas). Nuevamente, en teoría, el teclado que se muestra a continuación habría permitido que se ingresaran mediante el teclado aproximadamente 472 símbolos / funciones APL diferentes, utilizados activamente. En la práctica, las primeras versiones solo usaban algo aproximadamente equivalente a 55 símbolos especiales APL (excluyendo letras, números, puntuación, etc. teclas). Por lo tanto, el APL temprano solo usaba aproximadamente el 11% (55/472) del potencial de utilización de un lenguaje simbólico en ese momento, basado en los límites de las teclas del teclado, nuevamente excluyendo números, letras, puntuación, etc. En otro sentido, los símbolos del teclado la utilización fue más cercana al 100%, altamente eficiente, ya que EBCDIC solo permitía 256 caracteres distintos y ASCII solo 128.
Resolver acertijos
APL ha demostrado ser extremadamente útil para resolver acertijos matemáticos, varios de los cuales se describen a continuación.
Triángulo de Pascal
Tome el triángulo de Pascal , que es una matriz triangular de números en los que los que están en los extremos de las filas son 1 y cada uno de los otros números es la suma de los dos números más cercanos en la fila justo encima (el vértice, 1, está en la parte superior). La siguiente es una función APL de una sola línea para representar visualmente el triángulo de Pascal:
Pascal←{0~¨⍨a⌽⊃⌽∊¨0,¨¨a∘!¨a←⌽⍳⍵} ⍝ Create one-line user function called Pascal
Pascal 7 ⍝ Run function Pascal for seven rows and show the results below:
1
1 2
1 3 3
1 4 6 4
1 5 10 10 5
1 6 15 20 15 6
1 7 21 35 35 21 7
Números primos, contra prueba a través de factores
Determine el número de números primos (el número primo es un número natural mayor que 1 que no tiene divisores positivos distintos de 1 y él mismo) hasta cierto número N. A Ken Iverson se le atribuye la siguiente solución APL de una sola línea al problema:
⎕CR 'PrimeNumbers' ⍝ Show APL user-function PrimeNumbers
Primes←PrimeNumbers N ⍝ Function takes one right arg N (e.g., show prime numbers for 1 ... int N)
Primes←(2=+⌿0=(⍳N)∘.|⍳N)/⍳N ⍝ The Ken Iverson one-liner
PrimeNumbers 100 ⍝ Show all prime numbers from 1 to 100
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
⍴PrimeNumbers 100
25 ⍝ There are twenty-five prime numbers in the range up to 100.
Con frecuencia se necesita examinar el inverso o el opuesto de una solución matemática ( factores enteros de un número ): Demuestre para el subconjunto de números enteros del 1 al 15 que no son primos enumerando sus factores de descomposición . ¿Cuáles son sus factores distintos de uno (# divisible por, excepto 1)?
⎕CR 'ProveNonPrime'
Z←ProveNonPrime R
⍝Show all factors of an integer R - except 1 and the number itself,
⍝ i.e., prove Non-Prime. String 'prime' is returned for a Prime integer.
Z←(0=(⍳R)|R)/⍳R ⍝ Determine all factors for integer R, store into Z
Z←(~(Z∊1,R))/Z ⍝ Delete 1 and the number as factors for the number from Z.
→(0=⍴Z)/ProveNonPrimeIsPrime ⍝ If result has zero shape, it has no other factors and is therefore prime
Z←R,(⊂" factors(except 1) "),(⊂Z),⎕TCNL ⍝ Show the number R, its factors(except 1,itself), and a new line char
→0 ⍝ Done with function if non-prime
ProveNonPrimeIsPrime: Z←R,(⊂" prime"),⎕TCNL ⍝ function branches here if number was prime
ProveNonPrime ¨⍳15 ⍝ Prove non primes for each(¨) of the integers from 1 through 15 (iota 15)
1 prime
2 prime
3 prime
4 factors(except 1) 2
5 prime
6 factors(except 1) 2 3
7 prime
8 factors(except 1) 2 4
9 factors(except 1) 3
10 factors(except 1) 2 5
11 prime
12 factors(except 1) 2 3 4 6
13 prime
14 factors(except 1) 2 7
15 factors(except 1) 3 5
secuencia Fibonacci
Genere una secuencia numérica de Fibonacci , donde cada número subsiguiente en la secuencia es la suma de los dos anteriores:
⎕CR 'Fibonacci' ⍝ Display function Fibonacci
FibonacciNum←Fibonacci Nth;IOwas ⍝ Funct header, funct name=Fibonacci, monadic funct with 1 right hand arg Nth;local var IOwas, and a returned num.
⍝Generate a Fibonacci sequenced number where Nth is the position # of the Fibonacci number in the sequence. << function description
IOwas←⎕IO ⋄ ⎕IO←0 ⋄ FibonacciNum←↑0 1↓↑+.×/Nth/⊂2 2⍴1 1 1 0 ⋄ ⎕IO←IOwas ⍝ In order for this function to work correctly ⎕IO must be set to zero.
Fibonacci¨⍳14 ⍝ This APL statement says: Generate the Fibonacci sequence over each(¨) integer number(iota or ⍳) for the integers 1..14.
0 1 1 2 3 5 8 13 21 34 55 89 144 233 ⍝ Generated sequence, i.e., the Fibonacci sequence of numbers generated by APL's interpreter.
Otras lecturas
- Polivka, Raymond P .; Pakin, Sandra (1975). APL: El lenguaje y su uso . Prentice Hall. ISBN 978-0-13-038885-8.
- Reiter, Clifford A .; Jones, William R. (1990). APL con acento matemático (1 ed.). Taylor y Francis. ISBN 978-0534128647.
- Thompson, Norman D .; Polivka, Raymond P. (2013). APL2 in Depth (Springer Series in Statistics) (rústica) (Reimpresión del original 1ª ed.). Saltador. ISBN 978-0387942131.
- Gilman, Leonard; Rose, Allen J. (1976). APL: An Interactive Approach (rústica) (3ª ed.). ISBN 978-0471093046.
Ver también
- Técnico misceláneo : bloque Unicode que incluye claves APL
- APL (página de códigos) § Disposición del teclado : información más moderna sobre la distribución del teclado APL
Referencias
enlaces externos
- Referencia de caracteres APL: Página 1 , Página 2 , Página 3 , Página 4
- Página de fuentes de la Asociación Británica de APL
- Página de códigos de IBM 293 también conocida como la página de códigos APL en mainframes
- Información general sobre caracteres APL en el wiki de APL
- extendiendo APL y sus operadores de símbolos de teclado.
- Lee, Xah. "Cómo crear un diseño de teclado APL o símbolos matemáticos" . Consultado el 13 de enero de 2015 .
Tutoriales genéricos en línea
- Una introducción práctica a APL 1 y APL 2 por Graeme Donald Robertson
- APL para PC, servidores y tabletas: NARS con todas las funciones, sin restricciones, APL / 2 descargable gratis con matrices anidadas de Sudley Place Software
- Intérprete GNU APL descargable gratuito para APL por Jürgen Sauermann
- Tutoriales de YouTube APL subidos por Jimin Park, 8 videos instructivos de introducción / principiantes.
- Lista de tutoriales compilados de SIGAPL
- Aprenda APL: un tutorial de APL de MicroAPL
Reglas de sintaxis
- El juego de la vida de Conway en APL, en YouTube
- Iverson, Kenneth E. (1983). "Sintaxis y semántica APL" . ACM SIGAPL APL Quote Quote . 13 (3): 223–231. doi : 10.1145 / 800062.801221 . ISBN 978-0897910958.
- Gffer, M. (1989). "Un futuro APL: ejemplos y problemas" . Cuatrimoto de cotizaciones ACM SIGAPL APL . 19 (4): 158-163. doi : 10.1145 / 75144.75166 . ISBN 978-0897913270.