Spin network - Spin network

Red de espín simple del tipo utilizado en la gravedad cuántica de bucles

En física , una red de espín es un tipo de diagrama que se puede utilizar para representar estados e interacciones entre partículas y campos en mecánica cuántica . Desde una perspectiva matemática , los diagramas son una forma concisa de representar funciones multilineales y funciones entre representaciones de grupos de matrices . La notación diagramática a menudo simplifica el cálculo porque se pueden usar diagramas simples para representar funciones complicadas .

A Roger Penrose se le atribuye la invención de las redes de espín en 1971, aunque antes de su tiempo existían técnicas de diagramación similares. Las redes de espín han sido aplicadas a la teoría de la gravedad cuántica por Carlo Rovelli , Lee Smolin , Jorge Pullin , Rodolfo Gambini y otros.

Las redes de espín también se pueden usar para construir una función particular en el espacio de conexiones que es invariante bajo transformaciones de calibre local .

Definición

Definición original de Penrose

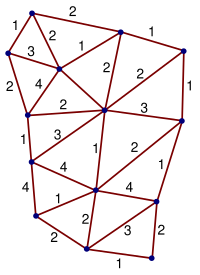
Una red de espín, como se describe en Penrose (1971), es una especie de diagrama en el que cada segmento de línea representa la línea del mundo de una "unidad" (ya sea una partícula elemental o un sistema compuesto de partículas). Tres segmentos de recta se unen en cada vértice. Un vértice se puede interpretar como un evento en el que una sola unidad se divide en dos o dos unidades chocan y se unen en una sola unidad. Los diagramas cuyos segmentos de línea están todos unidos en los vértices se denominan redes de espín cerradas . Se puede considerar que el tiempo va en una dirección, como de la parte inferior a la superior del diagrama, pero para las redes de espín cerradas, la dirección del tiempo es irrelevante para los cálculos.

Cada segmento de línea está etiquetado con un número entero llamado número de giro . Una unidad con número de espín n se llama n -unidad y tiene momento angular nħ / 2 , donde ħ es la constante de Planck reducida . Para bosones , como fotones y gluones , n es un número par. Para fermiones , como electrones y quarks , n es impar.

Dada cualquier red de espín cerrada, se puede calcular un número entero no negativo que se llama la norma de la red de espín. Las normas se pueden utilizar para calcular las probabilidades de varios valores de giro. Una red cuya norma es cero tiene una probabilidad de ocurrencia cero. Las reglas para calcular normas y probabilidades están más allá del alcance de este artículo. Sin embargo, implican que para que una red de espines tenga una norma distinta de cero, se deben cumplir dos requisitos en cada vértice. Supongamos que un vértice se une a tres unidades con números de espín una , b , y c . Entonces, estos requisitos se establecen como:

  • Triángulo de la desigualdad : una debe ser menor que o igual a b + c , b de menos de o igual a un + c , y c de menos de o igual a un + b .
  • Conservación de fermiones: a + b + c debe ser un número par.

Por ejemplo, a = 3, b = 4, c = 6 es imposible ya que 3 + 4 + 6 = 13 es impar, y a = 3, b = 4, c = 9 es imposible ya que 9> 3 + 4. Sin embargo, a = 3, b = 4, c = 5 es posible ya que 3 + 4 + 5 = 12 es par y se satisface la desigualdad del triángulo. Algunas convenciones usan etiquetas por medio enteros, con la condición de que la suma a + b + c debe ser un número entero.

Definicion formal

Más formalmente, una red de espín es un grafo (dirigido) cuyos bordes están asociados con representaciones irreductibles de un grupo de Lie compacto y cuyos vértices están asociados con entrelazadores de las representaciones de bordes adyacentes a él.

Una red de espín, sumergida en un colector, se puede utilizar para definir un funcional en el espacio de conexiones en este colector. Se calculan holonomías de la conexión a lo largo de cada enlace (camino cerrado) del gráfico, se determinan las matrices de representación correspondientes a cada enlace, se multiplican todas las matrices y se entrelazan juntos y se contraen los índices de una manera prescrita. Una característica notable del funcional resultante es que es invariante bajo transformaciones de calibre local .

Uso en física

En el contexto de la gravedad cuántica de bucles

En la gravedad cuántica de bucles (LQG), una red de espín representa un "estado cuántico" del campo gravitacional en una hipersuperficie tridimensional . El conjunto de todas las posibles redes de espín (o, más exactamente, " nudos s ", es decir, clases de equivalencia de redes de espín bajo difeomorfismos ) es contable ; constituye una base del espacio LQG Hilbert .

Uno de los resultados clave de la gravedad cuántica de bucles es la cuantificación de áreas: el operador del área A de una superficie bidimensional Σ debe tener un espectro discreto . Cada red de espín es un estado propio de cada uno de esos operadores, y el valor propio del área es igual a

donde la suma cubre todas las intersecciones i de Σ con la red de espín. En esta fórmula,

  • ℓ PL es la longitud de Planck ,
  • es el parámetro Immirzi y
  • j i = 0, 1/2, 1, 3/2, ... es el spin asociado con el enlace i de la red de spin. Por tanto, el área bidimensional se "concentra" en las intersecciones con la red de espín.

De acuerdo con esta fórmula, el valor propio más bajo posible distinto de cero del operador de área corresponde a un enlace que lleva representación de espín 1/2. Suponiendo un parámetro de Immirzi del orden de 1, esto da el área medible más pequeña posible de ~ 10 −66 cm 2 .

La fórmula de los valores propios del área se vuelve algo más complicada si se permite que la superficie pase a través de los vértices, como ocurre con los modelos de difusión anómalos. Además, los valores propios del operador de área A están restringidos por la simetría de escalera .

Se aplica una cuantificación similar al operador de volumen. El volumen de una subvariedad 3D que contiene parte de una red de espín viene dado por una suma de contribuciones de cada nodo dentro de ella. Uno puede pensar que cada nodo en una red de espín es un "cuanto de volumen" elemental y cada enlace es un "cuanto de área" que rodea este volumen.

Teorías de calibre más generales

Se pueden hacer construcciones similares para las teorías de calibre generales con un grupo de Lie compacto G y una forma de conexión . En realidad, se trata de una dualidad exacta sobre una red. Sin embargo, sobre una variedad , se necesitan suposiciones como la invariancia de difeomorfismo para hacer que la dualidad sea exacta (difuminar los bucles de Wilson es complicado). Posteriormente, fue generalizado por Robert Oeckl a representaciones de grupos cuánticos en 2 y 3 dimensiones utilizando la dualidad Tannaka-Kerin .

Michael A. Levin y Xiao-Gang Wen también han definido redes de cuerdas utilizando categorías de tensores que son objetos muy similares a las redes de espín. Sin embargo, la conexión exacta con las redes de spinning aún no está clara. La condensación de la red de cuerdas produce estados ordenados topológicamente en la materia condensada.

Uso en matemáticas

En matemáticas, las redes de espín se han utilizado para estudiar módulos de madejas y variedades de caracteres , que corresponden a espacios de conexiones .

Ver también

Referencias

Otras lecturas

Primeros trabajos

  • IB Levinson, "Suma de coeficientes de Wigner y su representación gráfica", Continúe. Phys-Tech Inst. Acad Sci. RSS de Lituania 2, 17-30 (1956)
  • Kogut, John; Susskind, Leonard (1975). "Formulación hamiltoniana de las teorías de calibre de celosía de Wilson". Physical Review D . 11 (2): 395–408. Código Bibliográfico : 1975PhRvD..11..395K . doi : 10.1103 / PhysRevD.11.395 .
  • Kogut, John B. (1983). "El enfoque de la teoría del calibre de celosía a la cromodinámica cuántica". Reseñas de Física Moderna . 55 (3): 775–836. Código Bibliográfico : 1983RvMP ... 55..775K . doi : 10.1103 / RevModPhys.55.775 . (consulte la sección euclidiana de alta temperatura (acoplamiento fuerte))
  • Savit, Robert (1980). "Dualidad en teoría de campo y sistemas estadísticos". Reseñas de Física Moderna . 52 (2): 453–487. Código Bibliográfico : 1980RvMP ... 52..453S . doi : 10.1103 / RevModPhys.52.453 . (ver las secciones sobre las teorías del calibre abeliano)

Papeles modernos

Libros

  • GE Stedman, Técnicas de diagrama en teoría de grupos , Cambridge University Press, 1990.
  • Predrag Cvitanović , Teoría de grupos: huellas de pájaros, mentiras y grupos excepcionales , Princeton University Press, 2008.