Rose (matemáticas) - Rose (mathematics)

Rosas especificadas por la sinusoide para varios valores numerados racionales de la frecuencia angular k = n / d . Las rosas especificadas por son rotaciones de estas rosas en un cuarto de período de la sinusoide en sentido contrario a las agujas del reloj alrededor del polo (origen). Para un análisis matemático adecuado, debe expresarse en forma irreductible.${\ Displaystyle r = \ cos (k \ theta)}$${\ Displaystyle r = \ sin (k \ theta)}$${\ Displaystyle k}$

En matemáticas , una curva rosa o rhodonea es una sinusoide especificada por las funciones coseno o seno sin ángulo de fase que se traza en coordenadas polares . Las curvas rosadas o "rhodonea" fueron nombradas por el matemático italiano que las estudió, Guido Grandi , entre los años 1723 y 1728.

Visión general

Especificación

Una rosa es el conjunto de puntos en coordenadas polares especificados por la ecuación polar.

${\ Displaystyle r = a \ cos (k \ theta)}$

o en coordenadas cartesianas usando las ecuaciones paramétricas

${\ Displaystyle x = r \ cos (\ theta) = a \ cos (k \ theta) \ cos (\ theta)}$

${\ Displaystyle y = r \ sin (\ theta) = a \ cos (k \ theta) \ sin (\ theta)}$.

Las rosas también se pueden especificar mediante la función seno. Desde

${\ Displaystyle \ sin (k \ theta) = \ cos \ left (k \ theta - {\ frac {\ pi} {2}} \ right) = \ cos \ left (k \ left (\ theta - {\ frac {\ pi} {2k}} \ right) \ right)}$.

Por lo tanto, la rosa especificada por es idéntica a la especificada por girada en el sentido contrario a las agujas del reloj en radianes, que es un cuarto del período de cualquiera de las sinusoides. ${\ Displaystyle \, r = a \ sin (k \ theta)}$${\ Displaystyle \, r = a \ cos (k \ theta)}$${\ Displaystyle \ pi / 2k}$

Dado que se especifican usando la función coseno o seno, las rosas generalmente se expresan como gráficos de coordenadas polares (en lugar de coordenadas cartesianas ) de sinusoides que tienen una frecuencia angular de y una amplitud de que determinan la coordenada radial dado el ángulo polar (aunque cuando es una número racional , una curva rosa se puede expresar en coordenadas cartesianas, ya que se pueden especificar como curvas algebraicas ). ${\ Displaystyle k}$${\ Displaystyle a}$${\ Displaystyle (r)}$${\ Displaystyle (\ theta)}$${\ Displaystyle k}$

Propiedades generales

Las rosas están directamente relacionadas con las propiedades de las sinusoides que las especifican.

Pétalos

• Los gráficos de rosas se componen de pétalos . Un pétalo es la forma formada por el gráfico de un semiciclo de la sinusoide que especifica la rosa. (Un ciclo es una parte de una sinusoide que tiene un período de duración y consta de un semiciclo positivo, el conjunto continuo de puntos donde y es largo, y un semiciclo negativo es la otra mitad ). ${\ Displaystyle T = 2 \ pi / k}$${\ Displaystyle r \ geq 0}$${\ Displaystyle T / 2 = \ pi / k}$${\ Displaystyle r \ leq 0}$
  • La forma de cada pétalo es la misma porque las gráficas de semiciclos tienen la misma forma. La forma viene dada por el semiciclo positivo con cresta en especificado por (que está delimitado por el intervalo de ángulo ). El pétalo es simétrico con respecto al eje polar. Todos los demás pétalos son rotaciones de este pétalo alrededor del polo, incluidas las de las rosas especificadas por la función seno con los mismos valores para y .${\ Displaystyle (a, 0)}$${\ Displaystyle r = a \ cos (k \ theta)}$${\ Displaystyle -T / 4 \ leq \ theta \ leq T / 4}$${\ Displaystyle a}$${\ Displaystyle k}$
  • De acuerdo con las reglas para trazar puntos en coordenadas polares, un punto en un semiciclo negativo no se puede trazar en su ángulo polar porque su coordenada radial es negativa. El punto se traza sumando radianes al ángulo polar con una coordenada radial . Por lo tanto, los semiciclos positivos y negativos pueden coincidir en el gráfico de una rosa. Además, las rosas están inscritas en el círculo .${\ Displaystyle r}$${\ Displaystyle \ pi}$${\ Displaystyle | r |}$${\ Displaystyle r = a}$
  • Cuando el período de la sinusoide es menor o igual a , la forma del pétalo es un solo bucle cerrado. Se forma un solo bucle porque el intervalo de ángulo para una gráfica polar es y el ancho angular del semiciclo es menor o igual a . Cuando (o ) la trama de un semiciclo puede verse como una espiral desde el polo en más de un circuito alrededor del polo hasta que la trama alcanza el círculo inscrito donde vuelve en espiral al polo, se cruza y forma uno o más bucles por el camino. En consecuencia, cada pétalo forma 2 bucles cuando (o ), 3 bucles cuando (o ), etc. Se observan rosas con un solo pétalo con múltiples bucles (Ver la figura en la sección de introducción).${\ Displaystyle T}$${\ Displaystyle 4 \ pi}$${\ Displaystyle 2 \ pi}$${\ Displaystyle 2 \ pi}$${\ Displaystyle T> 4 \ pi}$${\ Displaystyle | k | <1/2}$${\ Displaystyle 4 \ pi <T \ leq 8 \ pi}$${\ Displaystyle 1/4 \ leq | k | <1/2}$${\ Displaystyle 8 \ pi <T \ leq 12 \ pi}$${\ Displaystyle 1/6 \ leq | k | <1/4}$${\ Displaystyle k = 1/3, k = 1/5, k = 1/7, etc.}$
  • Los pétalos de una rosa no se cruzan entre sí cuando la frecuencia angular es un número entero distinto de cero; de lo contrario, los pétalos se cruzan entre sí.${\ Displaystyle k}$

Simetría

Todas las rosas muestran una o más formas de simetría debido a las propiedades simétricas y periódicas subyacentes de las sinusoides.

• Una rosa especificada como es simétrica con respecto al eje polar (la línea ) debido a la identidad que hace que las rosas especificadas por las dos ecuaciones polares coincidan.${\ Displaystyle r = a \ cos (k \ theta)}$${\ Displaystyle \ theta = 0}$ ${\ Displaystyle a \ cos (k \ theta) = a \ cos (-k \ theta)}$

• Una rosa especificada como es simétrica con respecto a la línea vertical debido a la identidad que hace que las rosas especificadas por las dos ecuaciones polares coincidan.${\ Displaystyle r = a \ sin (k \ theta)}$${\ Displaystyle \ theta = \ pi / 2}$${\ Displaystyle a \ sin (k \ theta) = a \ sin (\ pi -k \ theta)}$

• Solo ciertas rosas son simétricas con respecto al poste.

• Los pétalos individuales son simétricos con respecto a la línea que pasa por el polo y el pico del pétalo, lo que refleja la simetría del semiciclo del sinusoide subyacente. Las rosas compuestas por un número finito de pétalos son, por definición, rotacionalmente simétricas ya que cada pétalo tiene la misma forma con pétalos sucesivos rotados alrededor del mismo ángulo alrededor del polo.

Rosas con valores enteros distintos de cero de k

La rosa . Como es un número par, la rosa tiene pétalos. Los segmentos de línea que conectan picos sucesivos se encuentran en el círculo y formarán un octágono . Dado que un pico está en el octágono hace que trazar el gráfico sea relativamente fácil después de trazar los límites de medio ciclo (correspondientes a apotemas).${\ Displaystyle r = \ cos (4 \ theta)}$${\ Displaystyle k = 4}$${\ Displaystyle 2k = 8}$${\ Displaystyle r = 1}$${\ Displaystyle (1,0)}$

La rosa especificada por . Como es un número impar, la rosa tiene pétalos. Los segmentos de línea que conectan picos sucesivos se encuentran en el círculo y formarán un heptágono . La rosa está inscrita en el círculo .${\ Displaystyle r = \ cos (7 \ theta)}$${\ Displaystyle k = 7}$${\ Displaystyle k = 7}$${\ Displaystyle r = 1}$${\ Displaystyle r = 1}$

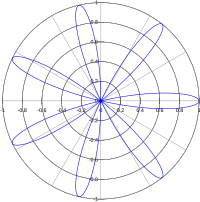
Cuando es un número entero distinto de cero, la curva tendrá forma de rosa con pétalos si es par, y pétalos cuando es impar. Las propiedades de estas rosas son un caso especial de rosas con frecuencias angulares que son números racionales discutidos en la siguiente sección de este artículo. ${\ Displaystyle k}$${\ displaystyle 2k}$ ${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle (k)}$

• La rosa está inscrita en el círculo , correspondiente a la coordenada radial de todos sus picos.${\ Displaystyle r = a}$

• Debido a que una gráfica de coordenadas polares se limita a ángulos polares entre y , se muestran ciclos en la gráfica. No es necesario trazar puntos adicionales porque la coordenada radial en tiene el mismo valor en (que son crestas para dos semiciclos positivos diferentes para rosas especificadas por la función coseno).${\ Displaystyle 0}$${\ Displaystyle 2 \ pi}$${\ Displaystyle 2 \ pi / T = k}$${\ Displaystyle \ theta = 0}$${\ Displaystyle \ theta = 2 \ pi}$

• Cuando es par (y diferente de cero), la rosa está compuesta de pétalos, uno por cada pico en el intervalo de ángulos polares mostrado. Cada pico corresponde a un punto que se encuentra en el círculo . Los segmentos de línea que conectan picos sucesivos formarán un polígono regular con un número par de vértices que tiene su centro en el polo y un radio a través de cada pico, y de la misma manera: ${\ Displaystyle k}$${\ displaystyle 2k}$${\ Displaystyle 2 \ pi}$${\ Displaystyle r = a}$
  • Las rosas son simétricas con respecto al poste.
  • Las rosas son simétricas alrededor de cada línea a través del polo y un pico (a través del "medio" un pétalo) con el ángulo polar entre los picos de pétalos sucesivos que son radianes. Por lo tanto, estas rosas tienen simetría rotacional de orden .${\ Displaystyle 2 \ pi / 2k = \ pi / k}$${\ displaystyle 2k}$
  • Las rosas son simétricas sobre cada línea que biseca el ángulo entre picos sucesivos, lo que corresponde a los límites de medio ciclo y la apotema del polígono correspondiente.

• Cuando es extraño, la rosa está compuesta por los pétalos, uno por cada cresta (o valle) en el intervalo de ángulos polares que se muestran. Cada pico corresponde a un punto que se encuentra en el círculo . Los semiciclos positivos y negativos de estas rosas son coincidentes, lo que significa que al graficarlos, solo los semiciclos positivos o solo los semiciclos negativos deben trazarse para formar la curva completa. (De manera equivalente, se graficará una curva completa trazando cualquier intervalo continuo de ángulos polares que tenga una longitud en radianes, como a ). Los segmentos de línea que conectan picos sucesivos formarán un polígono regular con un número impar de vértices, y de la misma manera: ${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle 2 \ pi}$${\ Displaystyle r = a}$${\ Displaystyle \ pi}$${\ Displaystyle \ theta = 0}$${\ Displaystyle \ theta = \ pi}$
  • Las rosas son simétricas alrededor de cada línea a través del polo y un pico (a través del "medio" un pétalo) con el ángulo polar entre los picos de pétalos sucesivos que son radianes. Por lo tanto, estas rosas tienen simetría rotacional de orden .${\ Displaystyle 2 \ pi / k}$${\ Displaystyle k}$

• Los pétalos de la rosa no se superponen.

• Las rosas se pueden especificar mediante curvas algebraicas de orden cuando k es impar y cuando k es par.${\ Displaystyle k + 1}$${\ Displaystyle 2 (k + 1)}$

El círculo

Una rosa con es un círculo que se encuentra en el poste con un diámetro que se encuentra en el eje polar cuando . El círculo es el único pétalo de la curva. (Vea el círculo que se forma al final de la siguiente sección.) En coordenadas cartesianas, las especificaciones equivalentes de coseno y seno son y , respectivamente. ${\ Displaystyle k = 1}$${\ Displaystyle r = a \ cos (\ theta)}$${\ displaystyle (xa / 2) ^ {2} + y ^ {2} = (a / 2) ^ {2}}$${\ displaystyle x ^ {2} + (ya / 2) ^ {2} = (a / 2) ^ {2}}$

El cuadrifolio

Una rosa con se llama cuadrifolio porque tiene 4 pétalos. En Coordenadas cartesianas, las especificaciones del coseno y del seno son y , respectivamente. ${\ Displaystyle k = 2}$${\ Displaystyle (x ^ {2} + y ^ {2}) ^ {3} = a ^ {2} (x ^ {2} -y ^ {2}) ^ {2}}$${\ Displaystyle (x ^ {2} + y ^ {2}) ^ {3} = 4 (axy) ^ {2}}$

El trifolio

Una rosa con se llama trifolio porque tiene 3 pétalos. La curva también se llama Paquerette de Mélibée. En Coordenadas cartesianas, las especificaciones del coseno y del seno son y , respectivamente. (Vea cómo se forma el trifolio al final de la siguiente sección). ${\ Displaystyle k = 3}$${\ Displaystyle (x ^ {2} + y ^ {2}) ^ {2} = a (x ^ {3} -3xy ^ {2})}$${\ Displaystyle (x ^ {2} + y ^ {2}) ^ {2} = - a (x ^ {3} -3xy ^ {2})}$

Áreas totales y de pétalos

El área total de una rosa con ecuación polar de la forma

${\ Displaystyle r = a \ cos (k \ theta)}$o , donde es un número entero distinto de cero, es${\ Displaystyle r = a \ sin (k \ theta) \,}$${\ Displaystyle k}$

${\ Displaystyle {\ frac {1} {2}} \ int _ {0} ^ {2 \ pi} (a \ cos (k \ theta)) ^ {2} \, d \ theta = {\ frac {a ^ {2}} {2}} \ left (\ pi + {\ frac {\ sin (4k \ pi)} {4k}} \ right) = {\ frac {\ pi a ^ {2}} {2} }}$, cuando es par; y${\ Displaystyle k}$

${\ Displaystyle {\ frac {1} {2}} \ int _ {0} ^ {\ pi} (a \ cos (k \ theta)) ^ {2} \, d \ theta = {\ frac {a ^ {2}} {2}} \ left ({\ frac {\ pi} {2}} + {\ frac {\ sin (2k \ pi)} {4k}} \ right) = {\ frac {\ pi a ^ {2}} {4}}}$, cuando es extraño.${\ Displaystyle k}$

Cuando es pareja, hay pétalos; y cuando es extraño, hay pétalos, por lo que el área de cada pétalo es . ${\ Displaystyle k}$${\ displaystyle 2k}$${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle {\ frac {\ pi a ^ {2}} {4k}}}$

Rosas con valores numéricos racionales para k

En general, cuando es un número racional en la forma de fracción irreducible , donde y son números enteros distintos de cero, el número de pétalos es el denominador de la expresión . Esto significa que el número de pétalos es si ambos y son impares y de lo contrario. ${\ Displaystyle k}$${\ Displaystyle k = n / d}$${\ Displaystyle n}$${\ Displaystyle d}$${\ Displaystyle 1 / 2-1 / (2k) = (nd) / 2n}$${\ Displaystyle n}$${\ Displaystyle n}$${\ Displaystyle d}$${\ Displaystyle 2n}$

• En el caso de que ambos y sean impares, los semiciclos positivos y negativos de la sinusoide son coincidentes. La gráfica de estas rosas se completa en cualquier intervalo continuo de ángulos polares que sea largo.${\ Displaystyle n}$${\ Displaystyle d}$${\ Displaystyle d \ pi}$

• Cuando es par y es impar, o viceversa, la rosa estará completamente graficada en un intervalo de ángulo polar continuo largo. Además, las rosas son simétricas con respecto al polo tanto para las especificaciones del coseno como del seno. ${\ Displaystyle n}$${\ Displaystyle d}$${\ Displaystyle 2d \ pi}$
  • Además, cuando es impar y es par, las rosas especificadas por las ecuaciones polares del coseno y del seno con los mismos valores de y son coincidentes. Para tal par de rosas, la rosa con la especificación de la función seno coincide con la cresta de la rosa con la especificación del coseno en el eje polar en o en . (Esto significa que las rosas y los valores enteros distintos de cero de nunca coinciden).${\ Displaystyle n}$${\ Displaystyle d}$${\ Displaystyle a}$${\ Displaystyle k}$${\ Displaystyle \ theta = d \ pi / 2}$${\ Displaystyle \ theta = 3d \ pi / 2}$${\ Displaystyle r = a \ cos (k \ theta)}$${\ Displaystyle r = a \ sin (k \ theta)}$${\ Displaystyle k}$

• La rosa está inscrita en el círculo , correspondiente a la coordenada radial de todos sus picos.${\ Displaystyle r = a}$

El folio de Durero

Una rosa con se llama folio de Durero, que lleva el nombre del pintor y grabador alemán Alberto Durero . Las rosas especificadas por y son coincidentes aunque . En Coordenadas cartesianas, la rosa se especifica como . ${\ Displaystyle k = 1/2}$${\ Displaystyle r = a \ cos (\ theta / 2)}$${\ Displaystyle r = a \ sin (\ theta / 2)}$${\ Displaystyle a \ cos (\ theta / 2) \ neq a \ sin (\ theta / 2)}$${\ Displaystyle (x ^ {2} + y ^ {2}) [2 (x ^ {2} + y ^ {2}) - a ^ {2}] ^ {2} = a ^ {4} x ^ {2}}$

El folio de Durero también es una trisectriz , una curva que se puede utilizar para trisecar ángulos.

El limaçon trisectrix

Una rosa con es una limaçon trisectrix que tiene la propiedad de curvas trisectrix que se pueden utilizar para trisecar ángulos. La rosa tiene un solo pétalo con dos bucles. (Vea la animación a continuación). ${\ Displaystyle k = 1/3}$

Ejemplos de rosas creadas con engranajes con diferentes proporciones. Los rayos mostrados son el eje polar y . La representación gráfica comienza en cuando es un número entero, de lo contrario, y continúa en el sentido de las agujas del reloj hasta .${\ Displaystyle r = \ cos (k \ theta)}$
${\ Displaystyle \ theta = \ pi / 2}$
${\ Displaystyle \ theta = 2 \ pi}$${\ Displaystyle k}$${\ Displaystyle \ theta = 2d \ pi}$${\ Displaystyle \ theta = 0}$

El círculo , k = 1 ( n = 1, d = 1). La rosa está completa cuando se alcanza (media revolución del engranaje más ligero).${\ Displaystyle \ theta = \ pi}$

La limaçon trisectrix , k = 1/3 ( n = 1, d = 3), tiene un pétalo con dos bucles. La rosa está completa cuando se alcanza (una revolución y media del engranaje más ligero).${\ Displaystyle \ theta = 3 \ pi}$

El trifolio, k = 3 ( n = 3, d = 1). La rosa está completa cuando se alcanza (media revolución del engranaje más ligero).${\ Displaystyle \ theta = \ pi}$

Los 8 pétalos de la rosa con k = 4/5 ( n = 4, d = 5) son cada uno, un solo bucle que se cruza con otros pétalos. La rosa es simétrica con respecto al polo. La rosa está completa a (cinco revoluciones de la marcha más ligera).${\ Displaystyle \ theta = 0}$

Rosas con valores numéricos irracionales para k

Una curva de rosa especificada con un número irracional de tiene un número infinito de pétalos y nunca se completará. Por ejemplo, la sinusoide tiene un período , por lo que tiene un pétalo en el intervalo del ángulo polar con una cresta en el eje polar; sin embargo, no hay otro ángulo polar en el dominio de la ecuación polar que se graficará en las coordenadas . En general, las rosas especificadas por sinusoides con frecuencias angulares que son constantes irracionales forman un conjunto denso (es decir, se acercan arbitrariamente a especificar cada punto del disco ). ${\ Displaystyle k}$${\ Displaystyle r = a \ cos (\ pi \ theta)}$${\ Displaystyle T = 2}$${\ Displaystyle -1/2 \ leq \ theta \ leq 1/2}$${\ Displaystyle (a, 0)}$${\ Displaystyle r \ leq a}$

Ver también

• Limaçon trisectrix - tiene la misma forma que la rosa con k = 1/3 .
• Quadrifolium : una curva rosa donde k = 2 .
• Rosa de Maurer
• Rose (topología)
• Sectrix de Maclaurin
• Espirógrafo

Notas

enlaces externos

Applet para crear rosa con parámetro k

• Diccionario visual de curvas planas especiales Xah Lee
• Ejemplo interactivo con JSXGraph
• Ejemplo interactivo con p5