Pruebas de identidades trigonométricas - Proofs of trigonometric identities

Los principales identidades trigonométricas entre las funciones trigonométricas se demostraron , utilizando principalmente la geometría del triángulo rectángulo . Para ángulos mayores y negativos , consulte Funciones trigonométricas .

Identidades trigonométricas elementales

Definiciones

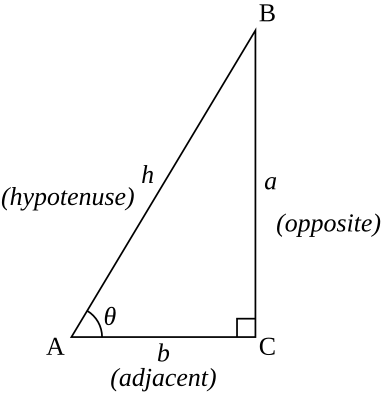
Las funciones trigonométricas especifican las relaciones entre las longitudes de los lados y los ángulos interiores de un triángulo rectángulo. Por ejemplo, el seno del ángulo θ se define como la longitud del lado opuesto dividida por la longitud de la hipotenusa.

Las seis funciones trigonométricas se definen para cada número real , excepto, para algunos de ellos, para ángulos que difieren de 0 en un múltiplo del ángulo recto (90 °). Con referencia al diagrama de la derecha, las seis funciones trigonométricas de θ son, para ángulos más pequeños que el ángulo recto:

${\ Displaystyle \ sin \ theta = {\ frac {\ mathrm {opuesto}} {\ mathrm {hipotenusa}}} = {\ frac {a} {h}}}$

${\ Displaystyle \ cos \ theta = {\ frac {\ mathrm {adyacente}} {\ mathrm {hipotenusa}}} = {\ frac {b} {h}}}$

${\ Displaystyle \ tan \ theta = {\ frac {\ mathrm {opuesto}} {\ mathrm {adyacente}}} = {\ frac {a} {b}}}$

${\ Displaystyle \ cot \ theta = {\ frac {\ mathrm {adyacente}} {\ mathrm {opuesto}}} = {\ frac {b} {a}}}$

${\ Displaystyle \ sec \ theta = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {adyacente}}} = {\ frac {h} {b}}}$

${\ Displaystyle \ csc \ theta = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {opuesto}}} = {\ frac {h} {a}}}$

Razón de identidades

En el caso de ángulos más pequeños que un ángulo recto, las siguientes identidades son consecuencias directas de las definiciones anteriores a través de la identidad de división

${\ Displaystyle {\ frac {a} {b}} = {\ frac {\ left ({\ frac {a} {h}} \ right)} {\ left ({\ frac {b} {h}} \ Derecha)}}.}$

Siguen siendo válidos para ángulos superiores a 90 ° y para ángulos negativos.

${\ Displaystyle \ tan \ theta = {\ frac {\ mathrm {opuesto}} {\ mathrm {adyacente}}} = {\ frac {\ left ({\ frac {\ mathrm {opuesto}} {\ mathrm {hipotenusa} }} \ right)} {\ left ({\ frac {\ mathrm {adyacente}} {\ mathrm {hipotenusa}}} \ right)}} = {\ frac {\ sin \ theta} {\ cos \ theta}} }$

${\ Displaystyle \ cot \ theta = {\ frac {\ mathrm {adyacente}} {\ mathrm {opuesto}}} = {\ frac {\ left ({\ frac {\ mathrm {adyacente}} {\ mathrm {adyacente} }} \ right)} {\ left ({\ frac {\ mathrm {opuesto}} {\ mathrm {adyacente}}} \ right)}} = {\ frac {1} {\ tan \ theta}} = {\ frac {\ cos \ theta} {\ sin \ theta}}}$

${\ Displaystyle \ sec \ theta = {\ frac {1} {\ cos \ theta}} = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {adyacente}}}}$

${\ Displaystyle \ csc \ theta = {\ frac {1} {\ sin \ theta}} = {\ frac {\ mathrm {hipotenusa}} {\ mathrm {opuesto}}}}$

${\ Displaystyle \ tan \ theta = {\ frac {\ mathrm {opuesto}} {\ mathrm {adyacente}}} = {\ frac {\ left ({\ frac {\ mathrm {opuesto} \ times \ mathrm {hipotenusa}) } {\ mathrm {opuesto} \ times \ mathrm {adyacente}}} \ right)} {\ left ({\ frac {\ mathrm {adyacente} \ times \ mathrm {hipotenusa}} {\ mathrm {opuesto} \ times \ mathrm {adyacente}}} \ right)}} = {\ frac {\ left ({\ frac {\ mathrm {hipotenusa}} {\ mathrm {adyacente}}} \ right)} {\ left ({\ frac {\ mathrm {hipotenusa}} {\ mathrm {opuesto}}} \ right)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}$

O

${\ Displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}} = {\ frac {\ left ({\ frac {1} {\ csc \ theta}} \ right)} { \ left ({\ frac {1} {\ sec \ theta}} \ right)}} = {\ frac {\ left ({\ frac {\ csc \ theta \ sec \ theta} {\ csc \ theta}} \ derecha)} {\ izquierda ({\ frac {\ csc \ theta \ sec \ theta} {\ sec \ theta}} \ right)}} = {\ frac {\ sec \ theta} {\ csc \ theta}}}$

${\ Displaystyle \ cot \ theta = {\ frac {\ csc \ theta} {\ sec \ theta}}}$

Identidades de ángulos complementarios

Dos ángulos cuya suma es π / 2 radianes (90 grados) son complementarios . En el diagrama, los ángulos en los vértices A y B son complementarios, por lo que podemos intercambiar ayb, y cambiar θ a π / 2 - θ, obteniendo:

${\ Displaystyle \ sin \ left (\ pi / 2- \ theta \ right) = \ cos \ theta}$

${\ Displaystyle \ cos \ left (\ pi / 2- \ theta \ right) = \ sin \ theta}$

${\ Displaystyle \ tan \ left (\ pi / 2- \ theta \ right) = \ cot \ theta}$

${\ Displaystyle \ cot \ left (\ pi / 2- \ theta \ right) = \ tan \ theta}$

${\ Displaystyle \ sec \ left (\ pi / 2- \ theta \ right) = \ csc \ theta}$

${\ Displaystyle \ csc \ left (\ pi / 2- \ theta \ right) = \ sec \ theta}$

Identidades pitagóricas

Identidad 1:

${\ Displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}$

Los siguientes dos resultados se derivan de esto y de las identidades de razón. Para obtener el primero, divida ambos lados de por ; para el segundo, dividir por . ${\ Displaystyle \ sin ^ {2} (x) + \ cos ^ {2} (x) = 1}$${\ Displaystyle \ cos ^ {2} (x)}$${\ Displaystyle \ sin ^ {2} (x)}$

${\ Displaystyle \ tan ^ {2} (x) +1 \ = \ sec ^ {2} (x)}$

${\ Displaystyle 1 \ + \ cot ^ {2} (x) = \ csc ^ {2} (x)}$

similar

${\ Displaystyle 1 \ + \ cot ^ {2} (x) = \ csc ^ {2} (x)}$

${\ Displaystyle \ csc ^ {2} (x) - \ cot ^ {2} (x) = 1}$

Identidad 2:

Lo siguiente explica las tres funciones recíprocas.

${\ Displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}$

Prueba 2:

Consulte el diagrama de triángulo anterior. Tenga en cuenta que por el teorema de Pitágoras . ${\ Displaystyle a ^ {2} + b ^ {2} = h ^ {2}}$

${\ Displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) = {\ frac {h ^ {2}} {a ^ {2}}} + {\ frac {h ^ {2 }} {b ^ {2}}} = {\ frac {a ^ {2} + b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2} + b ^ {2 }} {b ^ {2}}} = 2 \ + {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}} }}$

Sustituyendo con funciones apropiadas -

${\ Displaystyle 2 \ + {\ frac {b ^ {2}} {a ^ {2}}} + {\ frac {a ^ {2}} {b ^ {2}}} = 2 \ + \ tan ^ {2} (x) + \ cot ^ {2} (x)}$

El reordenamiento da:

${\ Displaystyle \ csc ^ {2} (x) + \ sec ^ {2} (x) - \ cot ^ {2} (x) = 2 \ + \ tan ^ {2} (x)}$

Identidades de suma de ángulos

Seno

Ilustración de la fórmula de la suma.

Dibuja una línea horizontal (el eje x ); marque un origen O. Dibuje una línea desde O en un ángulo por encima de la línea horizontal y una segunda línea en un ángulo por encima de ella; el ángulo entre la segunda línea y el eje x es . ${\ Displaystyle \ alpha}$${\ Displaystyle \ beta}$${\ Displaystyle \ alpha + \ beta}$

Coloque P en la línea definida por a una unidad de distancia del origen. ${\ Displaystyle \ alpha + \ beta}$

Sea PQ una línea perpendicular a la línea OQ definida por un ángulo , trazada desde el punto Q en esta línea hasta el punto P. OQP es un ángulo recto. ${\ Displaystyle \ alpha}$${\ Displaystyle \ por lo tanto}$

Sea QA una perpendicular desde el punto A en el eje x hasta Q y PB una perpendicular desde el punto B en el eje x hasta P. OAQ y OBP son ángulos rectos. ${\ Displaystyle \ por lo tanto}$

Dibuja R en PB para que QR sea paralelo al eje x .

Ahora ángulo (porque , haciendo , y finalmente ) ${\ Displaystyle RPQ = \ alpha}$${\ Displaystyle OQA = {\ frac {\ pi} {2}} - \ alpha}$${\ Displaystyle RQO = \ alpha, RQP = {\ frac {\ pi} {2}} - \ alpha}$${\ Displaystyle RPQ = \ alpha}$

${\ Displaystyle RPQ = {\ tfrac {\ pi} {2}} - RQP = {\ tfrac {\ pi} {2}} - ({\ tfrac {\ pi} {2}} - RQO) = RQO = \ alpha}$

${\ displaystyle OP = 1}$

${\ Displaystyle PQ = \ sin \ beta}$

${\ Displaystyle OQ = \ cos \ beta}$

${\ Displaystyle {\ frac {AQ} {OQ}} = \ sin \ alpha}$, asi que ${\ Displaystyle AQ = \ sin \ alpha \ cos \ beta}$

${\ Displaystyle {\ frac {PR} {PQ}} = \ cos \ alpha}$, asi que ${\ Displaystyle PR = \ cos \ alpha \ sin \ beta}$

${\ Displaystyle \ sin (\ alpha + \ beta) = PB = RB + PR = AQ + PR = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}$

Mediante la sustitución de y el uso de la simetría , también obtenemos: ${\ Displaystyle - \ beta}$${\ Displaystyle \ beta}$

${\ Displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos (- \ beta) + \ cos \ alpha \ sin (- \ beta)}$

${\ Displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta}$

Se puede dar otra prueba rigurosa, y mucho más sencilla, utilizando la fórmula de Euler , conocida a partir del análisis complejo. La fórmula de Euler es:

${\ Displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}$

Se deduce que para los ángulos y tenemos: ${\ Displaystyle \ alpha}$${\ Displaystyle \ beta}$

${\ Displaystyle e ^ {i (\ alpha + \ beta)} = \ cos (\ alpha + \ beta) + i \ sin (\ alpha + \ beta)}$

También usando las siguientes propiedades de funciones exponenciales:

${\ Displaystyle e ^ {i (\ alpha + \ beta)} = e ^ {i \ alpha} e ^ {i \ beta} = (\ cos \ alpha + i \ sin \ alpha) (\ cos \ beta + i \ sin \ beta)}$

Evaluación del producto:

${\ Displaystyle e ^ {i (\ alpha + \ beta)} = (\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta) + i (\ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha)}$

Igualar partes reales e imaginarias:

${\ Displaystyle \ cos (\ alpha + \ beta) = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta}$

${\ Displaystyle \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ sin \ beta \ cos \ alpha}$

Pero este es una especie de argumento circular , ya que la prueba de la fórmula de Euler requiere saber que la derivada del seno es el coseno, lo que solo se puede probar usando la identidad para el seno de la suma de dos ángulos.

Coseno

Usando la figura de arriba,

${\ displaystyle OP = 1}$

${\ Displaystyle PQ = \ sin \ beta}$

${\ Displaystyle OQ = \ cos \ beta}$

${\ Displaystyle {\ frac {OA} {OQ}} = \ cos \ alpha}$, asi que ${\ Displaystyle OA = \ cos \ alpha \ cos \ beta}$

${\ Displaystyle {\ frac {RQ} {PQ}} = \ sin \ alpha}$, asi que ${\ Displaystyle RQ = \ sin \ alpha \ sin \ beta}$

${\ Displaystyle \ cos (\ alpha + \ beta) = OB = OA-BA = OA-RQ = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}$

Mediante la sustitución de y el uso de la simetría , también obtenemos: ${\ Displaystyle - \ beta}$${\ Displaystyle \ beta}$

${\ Displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos (- \ beta) - \ sin \ alpha \ sin (- \ beta),}$

${\ Displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta}$

Además, usando las fórmulas de ángulos complementarios,

${\ Displaystyle {\ begin {alineado} \ cos (\ alpha + \ beta) & = \ sin \ left (\ pi / 2 - (\ alpha + \ beta) \ right) \\ & = \ sin \ left (( \ pi / 2- \ alpha) - \ beta \ right) \\ & = \ sin \ left (\ pi / 2- \ alpha \ right) \ cos \ beta - \ cos \ left (\ pi / 2- \ alpha \ derecha) \ sin \ beta \\ & = \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta \\\ end {alineado}}}$

Tangente y cotangente

De las fórmulas de seno y coseno, obtenemos

${\ Displaystyle \ tan (\ alpha + \ beta) = {\ frac {\ sin (\ alpha + \ beta)} {\ cos (\ alpha + \ beta)}} = {\ frac {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta} {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta}}}$

Dividiendo tanto el numerador como el denominador por , obtenemos ${\ Displaystyle \ cos \ alpha \ cos \ beta}$

${\ Displaystyle \ tan (\ alpha + \ beta) = {\ frac {\ tan \ alpha + \ tan \ beta} {1- \ tan \ alpha \ tan \ beta}}}$

Restar de , usar , ${\ Displaystyle \ beta}$${\ Displaystyle \ alpha}$${\ Displaystyle \ tan (- \ beta) = - \ tan \ beta}$

${\ Displaystyle \ tan (\ alpha - \ beta) = {\ frac {\ tan \ alpha + \ tan (- \ beta)} {1- \ tan \ alpha \ tan (- \ beta)}} = {\ frac {\ tan \ alpha - \ tan \ beta} {1+ \ tan \ alpha \ tan \ beta}}}$

De manera similar, de las fórmulas de seno y coseno, obtenemos

${\ Displaystyle \ cot (\ alpha + \ beta) = {\ frac {\ cos (\ alpha + \ beta)} {\ sin (\ alpha + \ beta)}} = {\ frac {\ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta} {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}}}$

Luego, al dividir tanto el numerador como el denominador entre , obtenemos ${\ Displaystyle \ sin \ alpha \ sin \ beta}$

${\ Displaystyle \ cot (\ alpha + \ beta) = {\ frac {\ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}$

O, usando , ${\ Displaystyle \ cot \ theta = {\ frac {1} {\ tan \ theta}}}$

${\ Displaystyle \ cot (\ alpha + \ beta) = {\ frac {1- \ tan \ alpha \ tan \ beta} {\ tan \ alpha + \ tan \ beta}} = {\ frac {{\ frac {1 } {\ tan \ alpha \ tan \ beta}} - 1} {{\ frac {1} {\ tan \ alpha}} + {\ frac {1} {\ tan \ beta}}}} = {\ frac { \ cot \ alpha \ cot \ beta -1} {\ cot \ alpha + \ cot \ beta}}}$

Usando , ${\ Displaystyle \ cot (- \ beta) = - \ cot \ beta}$

${\ Displaystyle \ cot (\ alpha - \ beta) = {\ frac {\ cot \ alpha \ cot (- \ beta) -1} {\ cot \ alpha + \ cot (- \ beta)}} = {\ frac {\ cot \ alpha \ cot \ beta +1} {\ cot \ beta - \ cot \ alpha}}}$

Identidades de doble ángulo

De las identidades de suma de ángulos, obtenemos

${\ Displaystyle \ sin (2 \ theta) = 2 \ sin \ theta \ cos \ theta}$

y

${\ Displaystyle \ cos (2 \ theta) = \ cos ^ {2} \ theta - \ sin ^ {2} \ theta}$

Las identidades pitagóricas dan las dos formas alternativas para la última de estas:

${\ Displaystyle \ cos (2 \ theta) = 2 \ cos ^ {2} \ theta -1}$

${\ Displaystyle \ cos (2 \ theta) = 1-2 \ sin ^ {2} \ theta}$

Las identidades de suma de ángulos también dan

${\ Displaystyle \ tan (2 \ theta) = {\ frac {2 \ tan \ theta} {1- \ tan ^ {2} \ theta}} = {\ frac {2} {\ cot \ theta - \ tan \ theta}}}$

${\ Displaystyle \ cot (2 \ theta) = {\ frac {\ cot ^ {2} \ theta -1} {2 \ cot \ theta}} = {\ frac {\ cot \ theta - \ tan \ theta} { 2}}}$

También se puede probar usando la fórmula de Euler.

${\ Displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi}$

Cuadrar ambos lados rinde

${\ Displaystyle e ^ {i2 \ varphi} = (\ cos \ varphi + i \ sin \ varphi) ^ {2}}$

Pero al reemplazar el ángulo con su versión duplicada, que logra el mismo resultado en el lado izquierdo de la ecuación, se obtiene

${\ Displaystyle e ^ {i2 \ varphi} = \ cos 2 \ varphi + i \ sin 2 \ varphi}$

Resulta que

${\ Displaystyle (\ cos \ varphi + i \ sin \ varphi) ^ {2} = \ cos 2 \ varphi + i \ sin 2 \ varphi}$.

Expandir el cuadrado y simplificar en el lado izquierdo de la ecuación da

${\ Displaystyle i (2 \ sin \ varphi \ cos \ varphi) + \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi + i \ sin 2 \ varphi}$.

Debido a que las partes imaginaria y real tienen que ser iguales, nos quedamos con las identidades originales.

${\ Displaystyle \ cos ^ {2} \ varphi - \ sin ^ {2} \ varphi \ = \ cos 2 \ varphi}$,

y también

${\ Displaystyle 2 \ sin \ varphi \ cos \ varphi = \ sin 2 \ varphi}$.

Identidades de medio ángulo

Las dos identidades que dan las formas alternativas para cos 2θ conducen a las siguientes ecuaciones:

${\ Displaystyle \ cos {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {2}}},}$

${\ Displaystyle \ sin {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {2}}}.}$

El signo de la raíz cuadrada debe elegirse correctamente; tenga en cuenta que si se suma 2 π a θ, las cantidades dentro de las raíces cuadradas no cambian, pero los lados izquierdos de las ecuaciones cambian de signo. Por tanto, el signo correcto a utilizar depende del valor de θ.

Para la función tan, la ecuación es:

${\ Displaystyle \ tan {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}}.}$

Luego, multiplicar el numerador y el denominador dentro de la raíz cuadrada por (1 + cos θ) y usar identidades pitagóricas conduce a:

${\ Displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {\ sin \ theta} {1+ \ cos \ theta}}.}$

Además, si el numerador y el denominador se multiplican por (1 - cos θ), el resultado es:

${\ Displaystyle \ tan {\ frac {\ theta} {2}} = {\ frac {1- \ cos \ theta} {\ sin \ theta}}.}$

Esto también da:

${\ Displaystyle \ tan {\ frac {\ theta} {2}} = \ csc \ theta - \ cot \ theta.}$

Manipulaciones similares para la función cot dan:

${\ Displaystyle \ cot {\ frac {\ theta} {2}} = \ pm \, {\ sqrt {\ frac {1+ \ cos \ theta} {1- \ cos \ theta}}} = {\ frac { 1+ \ cos \ theta} {\ sin \ theta}} = {\ frac {\ sin \ theta} {1- \ cos \ theta}} = \ csc \ theta + \ cot \ theta.}$

Varios: la identidad de la triple tangente

Si un medio círculo (por ejemplo, , y son los ángulos de un triángulo), ${\ Displaystyle \ psi + \ theta + \ phi = \ pi =}$${\ Displaystyle \ psi}$${\ Displaystyle \ theta}$${\ Displaystyle \ phi}$

${\ Displaystyle \ tan (\ psi) + \ tan (\ theta) + \ tan (\ phi) = \ tan (\ psi) \ tan (\ theta) \ tan (\ phi).}$

Prueba:

${\ Displaystyle {\ begin {alineado} \ psi & = \ pi - \ theta - \ phi \\\ tan (\ psi) & = \ tan (\ pi - \ theta - \ phi) \\ & = - \ tan (\ theta + \ phi) \\ & = {\ frac {- \ tan \ theta - \ tan \ phi} {1- \ tan \ theta \ tan \ phi}} \\ & = {\ frac {\ tan \ theta + \ tan \ phi} {\ tan \ theta \ tan \ phi -1}} \\ (\ tan \ theta \ tan \ phi -1) \ tan \ psi & = \ tan \ theta + \ tan \ phi \ \\ tan \ psi \ tan \ theta \ tan \ phi - \ tan \ psi & = \ tan \ theta + \ tan \ phi \\\ tan \ psi \ tan \ theta \ tan \ phi & = \ tan \ psi + \ tan \ theta + \ tan \ phi \\\ end {alineado}}}$

Varios: la triple identidad cotangente

Si es un cuarto de círculo, ${\ Displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}} =}$

${\ Displaystyle \ cot (\ psi) + \ cot (\ theta) + \ cot (\ phi) = \ cot (\ psi) \ cot (\ theta) \ cot (\ phi)}$.

Prueba:

Reemplace cada uno de , y con sus ángulos complementarios, de modo que las cotangentes se conviertan en tangentes y viceversa. ${\ Displaystyle \ psi}$${\ Displaystyle \ theta}$${\ Displaystyle \ phi}$

Dado

${\ Displaystyle \ psi + \ theta + \ phi = {\ tfrac {\ pi} {2}}}$

${\ Displaystyle \ por lo tanto ({\ tfrac {\ pi} {2}} - \ psi) + ({\ tfrac {\ pi} {2}} - \ theta) + ({\ tfrac {\ pi} {2} } - \ phi) = {\ tfrac {3 \ pi} {2}} - (\ psi + \ theta + \ phi) = {\ tfrac {3 \ pi} {2}} - {\ tfrac {\ pi} {2}} = \ pi}$

por lo que el resultado se sigue de la identidad de la triple tangente.

Suma de identidades de productos

• ${\ Displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}$
• ${\ Displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$
• ${\ Displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$

Prueba de identidades sinusoidales

Primero, comience con las identidades de la suma de ángulos:

${\ Displaystyle \ sin (\ alpha + \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta}$

${\ Displaystyle \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta}$

Sumando estos juntos,

${\ Displaystyle \ sin (\ alpha + \ beta) + \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta + \ sin \ alpha \ cos \ beta - \ cos \ alpha \ sin \ beta = 2 \ sin \ alpha \ cos \ beta}$

De manera similar, al restar las dos identidades de la suma de los ángulos,

${\ Displaystyle \ sin (\ alpha + \ beta) - \ sin (\ alpha - \ beta) = \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta - \ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ beta = 2 \ cos \ alpha \ sin \ beta}$

Deje y , ${\ Displaystyle \ alpha + \ beta = \ theta}$${\ Displaystyle \ alpha - \ beta = \ phi}$

${\ Displaystyle \ por lo tanto \ alpha = {\ frac {\ theta + \ phi} {2}}}$ y ${\ Displaystyle \ beta = {\ frac {\ theta - \ phi} {2}}}$

Sustituir y${\ Displaystyle \ theta}$${\ Displaystyle \ phi}$

${\ Displaystyle \ sin \ theta + \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$

${\ Displaystyle \ sin \ theta - \ sin \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi } {2}} \ right) = 2 \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta + \ phi} {2} }\Derecha)}$

Por lo tanto,

${\ Displaystyle \ sin \ theta \ pm \ sin \ phi = 2 \ sin \ left ({\ frac {\ theta \ pm \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta \ mp \ phi} {2}} \ right)}$

Prueba de identidades coseno

De manera similar, para el coseno, comience con las identidades de la suma de ángulos:

${\ Displaystyle \ cos (\ alpha + \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta}$

${\ Displaystyle \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta}$

Nuevamente, sumando y restando

${\ Displaystyle \ cos (\ alpha + \ beta) + \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta + \ cos \ alpha \ cos \ beta + \ sin \ alpha \ sin \ beta = 2 \ cos \ alpha \ cos \ beta}$

${\ Displaystyle \ cos (\ alpha + \ beta) - \ cos (\ alpha - \ beta) = \ cos \ alpha \ cos \ beta \ - \ sin \ alpha \ sin \ beta - \ cos \ alpha \ cos \ beta - \ sin \ alpha \ sin \ beta = -2 \ sin \ alpha \ sin \ beta}$

Sustituir y como antes, ${\ Displaystyle \ theta}$${\ Displaystyle \ phi}$

${\ Displaystyle \ cos \ theta + \ cos \ phi = 2 \ cos \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ cos \ left ({\ frac {\ theta - \ phi } {2}} \ right)}$

${\ Displaystyle \ cos \ theta - \ cos \ phi = -2 \ sin \ left ({\ frac {\ theta + \ phi} {2}} \ right) \ sin \ left ({\ frac {\ theta - \ phi} {2}} \ right)}$

Desigualdades

Ilustración de las desigualdades de seno y tangente.

La figura de la derecha muestra un sector de un círculo con radio 1. El sector es θ / (2 π ) del círculo completo, por lo que su área es θ / 2 . Suponemos aquí que θ < π / 2 .

${\ displaystyle OA = OD = 1}$

${\ Displaystyle AB = \ sin \ theta}$

${\ Displaystyle CD = \ tan \ theta}$

El área del triángulo OAD es AB / 2 o sin ( θ ) / 2 . El área del triángulo OCD es CD / 2 o tan ( θ ) / 2 .

Dado que el triángulo OAD se encuentra completamente dentro del sector, que a su vez se encuentra completamente dentro del triángulo OCD , tenemos

${\ Displaystyle \ sin \ theta <\ theta <\ tan \ theta.}$

Este argumento geométrico se basa en definiciones de longitud y área de arco , que actúan como suposiciones, por lo que es más una condición impuesta en la construcción de funciones trigonométricas que una propiedad demostrable. Para la función seno, podemos manejar otros valores. Si θ > π / 2 , entonces θ > 1 . Pero sin θ ≤ 1 (debido a la identidad pitagórica), entonces sin θ < θ . Entonces tenemos

${\ Displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 \ \ \ \ mathrm {if} \ \ \ 0 <\ theta.}$

Para valores negativos de θ tenemos, por la simetría de la función seno

${\ Displaystyle {\ frac {\ sin \ theta} {\ theta}} = {\ frac {\ sin (- \ theta)} {- \ theta}} <1.}$

Por eso

${\ Displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 \ quad {\ text {if}} \ quad \ theta \ neq 0,}$

y

${\ Displaystyle {\ frac {\ tan \ theta} {\ theta}}> 1 \ quad {\ text {if}} \ quad 0 <\ theta <{\ frac {\ pi} {2}}.}$

Identidades que involucran cálculo

Preliminares

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ sin \ theta} = 0}$

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}$

Identidad de relación de seno y ángulo

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}$

En otras palabras, la función seno es diferenciable en 0 y su derivada es 1.

Prueba: De las desigualdades anteriores, tenemos, para ángulos pequeños

${\ Displaystyle \ sin \ theta <\ theta <\ tan \ theta}$,

Por lo tanto,

${\ Displaystyle {\ frac {\ sin \ theta} {\ theta}} <1 <{\ frac {\ tan \ theta} {\ theta}}}$,

Considere la desigualdad de la derecha. Ya que

${\ Displaystyle \ tan \ theta = {\ frac {\ sin \ theta} {\ cos \ theta}}}$

${\ Displaystyle \ por lo tanto 1 <{\ frac {\ sin \ theta} {\ theta \ cos \ theta}}}$

Multiplica por ${\ Displaystyle \ cos \ theta}$

${\ Displaystyle \ cos \ theta <{\ frac {\ sin \ theta} {\ theta}}}$

Combinando con la desigualdad de la izquierda:

${\ Displaystyle \ cos \ theta <{\ frac {\ sin \ theta} {\ theta}} <1}$

Llevando al límite como${\ Displaystyle \ cos \ theta}$${\ Displaystyle \ theta \ to 0}$

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ cos \ theta} = 1}$

Por lo tanto,

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ frac {\ sin \ theta} {\ theta}} = 1}$

Identidad de relación de coseno y ángulo

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta}} = 0}$

Prueba:

${\ Displaystyle {\ begin {alineado} {\ frac {1- \ cos \ theta} {\ theta}} & = {\ frac {1- \ cos ^ {2} \ theta} {\ theta (1+ \ cos \ theta)}} \\ & = {\ frac {\ sin ^ {2} \ theta} {\ theta (1+ \ cos \ theta)}} \\ & = \ left ({\ frac {\ sin \ theta } {\ theta}} \ right) \ times \ sin \ theta \ times \ left ({\ frac {1} {1+ \ cos \ theta}} \ right) \\\ end {alineado}}}$

Los límites de esas tres cantidades son 1, 0 y 1/2, por lo que el límite resultante es cero.

Coseno y cuadrado de identidad de relación angular

${\ Displaystyle \ lim _ {\ theta \ to 0} {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {1} {2}}}$

Prueba:

Como en la prueba anterior,

${\ Displaystyle {\ frac {1- \ cos \ theta} {\ theta ^ {2}}} = {\ frac {\ sin \ theta} {\ theta}} \ times {\ frac {\ sin \ theta} { \ theta}} \ times {\ frac {1} {1+ \ cos \ theta}}.}$

Los límites de esas tres cantidades son 1, 1 y 1/2, por lo que el límite resultante es 1/2.

Prueba de composición de funciones trigonométricas y trigonométricas inversas

Todas estas funciones se derivan de la identidad trigonométrica pitagórica. Podemos probar, por ejemplo, la función

${\ Displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {1 + x ^ {2}}}}}$

Prueba:

Partimos de

${\ Displaystyle \ sin ^ {2} \ theta + \ cos ^ {2} \ theta = 1}$

Luego dividimos esta ecuación por ${\ Displaystyle \ cos ^ {2} \ theta}$

${\ Displaystyle \ cos ^ {2} \ theta = {\ frac {1} {\ tan ^ {2} \ theta +1}}}$

Luego usa la sustitución , también usa la identidad trigonométrica pitagórica: ${\ Displaystyle \ theta = \ arctan (x)}$

${\ Displaystyle 1- \ sin ^ {2} [\ arctan (x)] = {\ frac {1} {\ tan ^ {2} [\ arctan (x)] + 1}}}$

Entonces usamos la identidad ${\ Displaystyle \ tan [\ arctan (x)] \ equiv x}$

${\ Displaystyle \ sin [\ arctan (x)] = {\ frac {x} {\ sqrt {x ^ {2} +1}}}}$

Ver también

Notas

Referencias