Cálculo mental - Mental calculation

El cálculo mental ha sido durante mucho tiempo un componente de la educación matemática.

El cálculo mental consiste en cálculos aritméticos que utilizan solo el cerebro humano , sin la ayuda de ningún material (como lápiz y papel) o dispositivos como una calculadora . Las personas utilizan el cálculo mental cuando no se dispone de herramientas informáticas, cuando es más rápido que otros medios de cálculo (como los métodos convencionales de las instituciones educativas) o incluso en un contexto competitivo . El cálculo mental a menudo implica el uso de técnicas específicas diseñadas para tipos específicos de problemas. Las personas con una capacidad inusualmente alta para realizar cálculos mentales se denominan calculadoras mentales o calculadoras de rayos .

Muchas de estas técnicas aprovechan o se basan en el sistema de numeración decimal . Por lo general, la elección de la base es lo que determina qué método o métodos utilizar.

Métodos y técnicas

Lanzando nueves

Después de aplicar una operación aritmética a dos operandos y obtener un resultado, se puede utilizar el siguiente procedimiento para mejorar la confianza en la exactitud del resultado:

Suma los dígitos del primer operando; cualquier 9 (o conjuntos de dígitos que sumen 9) se pueden contar como 0.
Si la suma resultante tiene dos o más dígitos, sume esos dígitos como en el paso uno; repita este paso hasta que la suma resultante tenga solo un dígito.
Repita los pasos uno y dos con el segundo operando. Hay dos números de un solo dígito, uno condensado del primer operando y el otro condensado del segundo operando. (Estos números de un solo dígito son también los restos con los que se terminaría si se dividieran los operandos originales por 9; matemáticamente hablando, son los operandos originales módulo 9.)
Aplique la operación especificada originalmente a los dos operandos condensados y luego aplique el procedimiento de suma de dígitos al resultado de la operación.
Sume los dígitos del resultado que se obtuvieron originalmente para el cálculo original.
Si el resultado del paso 4 no es igual al resultado del paso 5, entonces la respuesta original es incorrecta. Si los dos resultados coinciden, entonces la respuesta original puede ser correcta, aunque no se garantiza que lo sea.

Ejemplo

Digamos que el cálculo da como resultado que 6338 × 79 es igual a 500702

Suma los dígitos de 6338: (6 + 3 = 9, así que cuenta eso como 0) + 3 + 8 = 11
Iterar según sea necesario: 1 + 1 = 2
Suma los dígitos de 79: 7 + (9 contados como 0) = 7
Realice la operación original en los operandos condensados y suma dígitos: 2 × 7 = 14; 1 + 4 = 5
Suma los dígitos de 500702: 5 + 0 + 0 + (7 + 0 + 2 = 9, que cuenta como 0) = 5
5 = 5, por lo que hay una buena probabilidad de que la predicción de que 6338 × 79 es igual a 500702 sea correcta.

El mismo procedimiento se puede utilizar con varias operaciones, repitiendo los pasos 1 y 2 para cada operación.

Estimacion

Al comprobar el cálculo mental, es útil pensar en él en términos de escala. Por ejemplo, cuando se trata de números grandes, digamos 1 531 × 19 625, la estimación le indica a uno que tenga en cuenta el número de dígitos esperado para el valor final. Una forma útil de verificar es estimar. 1 531 es alrededor de 1 500 y 19 625 es alrededor de 20 000, por lo que un resultado de alrededor de 20 000 × 1 500 (30 000 000) sería una buena estimación para la respuesta real (30 045 875). Entonces, si la respuesta tiene demasiados dígitos, se ha cometido un error.

Factores

Al multiplicar, es útil recordar que los factores de los operandos aún permanecen. Por ejemplo, decir que 14 × 15 era 201 no sería razonable. Dado que 15 es un múltiplo de 5, el producto también debería serlo. Asimismo, 14 es un múltiplo de 2, por lo que el producto debe ser par. Además, cualquier número que sea múltiplo de 5 y 2 es necesariamente un múltiplo de 10, y en el sistema decimal terminaría con un 0. La respuesta correcta es 210. Es un múltiplo de 10, 7 (el otro factor primo de 14) y 3 (el otro factor primo de 15).

Cálculo de diferencias: a - b

Cálculo directo

Cuando los dígitos de b son todos más pequeños que los dígitos correspondientes de a , el cálculo se puede hacer dígito a dígito. Por ejemplo, evalúe 872 - 41 simplemente restando 1 de 2 en el lugar de las unidades y 4 de 7 en el lugar de las decenas: 831.

Cálculo indirecto

Cuando la situación anterior no se aplica, existe otro método conocido como cálculo indirecto.

Método de préstamo anticipado

Este método puede usarse para restar números de izquierda a derecha, y si todo lo que se requiere es leer el resultado en voz alta, se requiere poca memoria del usuario, incluso para restar números de tamaño arbitrario.

Se maneja un lugar a la vez, de izquierda a derecha.

Example:

          4075
        − 1844
        ------

Thousands: 4 − 1 = 3, look to right, 075 < 844, need to borrow.
           3 − 1 = 2, say "Two thousand".
           One is performing 3 - 1 rather than 4 - 1 because the column to the right is
           going to borrow from the thousands place.

Hundreds: 0 − 8 = negative numbers not allowed here.
          One is going to increase this place by using the number one borrowed from the
          column to the left. Therefore:
          10 − 8 = 2. It's 10 rather than 0, because one borrowed from the Thousands
          place. 75 > 44 so no need to borrow,
          say "two hundred"

Tens: 7 − 4 = 3, 5 > 4, so 5 - 4 = 1

Por tanto, el resultado es 2231.

Cálculo de productos: a × b

Muchos de estos métodos funcionan debido a la propiedad distributiva .

Multiplicar dos números cualesquiera sumando, restando y enrutando

Descubierto por Artem Cheprasov, existe un método de multiplicación que permite al usuario utilizar 3 pasos para multiplicar rápidamente números de cualquier tamaño entre sí a través de tres formas únicas.

Primero, el método permite al usuario adjuntar números entre sí, en lugar de sumarlos o restarlos, durante los pasos intermedios para acelerar la tasa de multiplicación. Por ejemplo, en lugar de sumar o restar resultados intermedios como 357 y 84, el usuario podría simplemente unir los números (35784) para simplificar y acelerar el problema de multiplicación. Unir números entre sí ayuda a evitar los pasos innecesarios que se encuentran en las técnicas tradicionales de multiplicación.

En segundo lugar, este método utiliza números negativos según sea necesario, incluso cuando se multiplican dos enteros positivos, para acelerar la tasa de multiplicación mediante la resta. Esto significa que dos números enteros positivos se pueden multiplicar para obtener pasos intermedios negativos, pero aún así la respuesta positiva correcta al final. Estos números negativos en realidad se derivan automáticamente de los pasos de multiplicación mismos y, por lo tanto, son exclusivos de un problema en particular. Una vez más, estos pasos intermedios negativos están diseñados para ayudar a acelerar la matemática mental.

Finalmente, otro aspecto único del uso de este método es que el usuario puede elegir una de varias “rutas de multiplicación” diferentes para el problema de multiplicación específico en cuestión en función de sus preferencias subjetivas o fortalezas y debilidades con números enteros particulares.

A pesar de los mismos números enteros iniciales, las diferentes rutas de multiplicación emiten diferentes números intermedios que se derivan automáticamente para el usuario a medida que se multiplican. Algunos de estos intermediarios pueden ser más fáciles que otros (por ejemplo, algunos usuarios pueden encontrar una ruta que usa un 7 negativo, mientras que otra ruta usa un 5 o un 0, que suelen ser más fáciles de trabajar mentalmente para la mayoría de las personas, pero no en todos los casos. ).

Si una "ruta" parece ser más difícil para un estudiante en comparación con otra ruta y sus números intermedios, ese estudiante puede simplemente elegir otra ruta más simple de multiplicación por sí mismo, aunque sea el mismo problema original.

La fórmula "Fines de cinco"

Para cualquier problema de multiplicación de 2 dígitos por 2 dígitos, si ambos números terminan en cinco, se puede usar el siguiente algoritmo para multiplicarlos rápidamente:

${\ Displaystyle Ej .: 35 \ times 75}$

Como paso preliminar, simplemente redondee el número más pequeño hacia abajo y el mayor al múltiplo de diez más cercano. En este caso:

${\ textstyle 35-5 = 30 = X}$

${\ displaystyle 75 + 5 = 80 = Y}$

El algoritmo dice lo siguiente:

${\ Displaystyle (X \ times Y) +50 (t_ {1} -t_ {2}) + 25}$

Donde t ₁ es la unidad de las decenas del número original más grande (75) y t ₂ es la unidad de las decenas del número original más pequeño (35).

${\ displaystyle = 30 \ times 80 + 50 (7-3) + 25 = 2625}$

El autor también describe otro algoritmo similar si se quiere redondear el número original más grande hacia abajo y el número original más pequeño hacia arriba.

La fórmula del "prestatario"

Si dos números son equidistantes del múltiplo más cercano de 100, entonces se puede usar un algoritmo simple para encontrar el producto.

Como un simple ejemplo:

${\ Displaystyle 33 \ times 67}$

Ambos números son equidistantes (33 de distancia) de su múltiplo más cercano de 100 (0 y 100, respectivamente).

Como paso preliminar, simplemente redondee el número más pequeño hacia abajo y el mayor al múltiplo de diez más cercano. En este caso:

${\ textstyle 33-3 = 30 = X}$

${\ displaystyle 67 + 3 = 70 = Y}$

El algoritmo dice lo siguiente:

${\ Displaystyle (X \ times Y) + u_ {1} \ times u_ {2} + u_ {2} (T_ {1} -T_ {2})}$

Donde u ₁ es el dígito de unidades del número mayor original (67) y u ₂ es el dígito de unidades del número original menor (33). T ₁ es el dígito de las decenas del número mayor original y T ₂ es el dígito de las decenas del número mayor original multiplicado por su respectiva potencia (en este caso por 10, para un dígito de decenas).

Y entonces:

${\ displaystyle (30 \ times 70) +7 \ times 3 + 3 (60-30) = 2100 + 21 + 90 = 2211}$

Multiplicar cualquier número de 2 dígitos

Para multiplicar fácilmente cualquier número de 2 dígitos, un algoritmo simple es el siguiente (donde a es el dígito de las decenas del primer número, b es el dígito de las unidades del primer número, c es el dígito de las decenas del segundo número y d es el el dígito de las unidades del segundo número):

{\ Displaystyle (10a + b) \ cdot (10c + d)}

{\ Displaystyle = 100 (a \ cdot c) +10 (segundo \ cdot c) +10 (a \ cdot d) + b \ cdot d}

Por ejemplo,

{\ Displaystyle 23 \ cdot 47 = 100 (2 \ cdot 4) +10 (3 \ cdot 4) +10 (2 \ cdot 7) +3 \ cdot 7}

  800
 +120
 +140
 + 21
-----
 1081

Tenga en cuenta que esto es lo mismo que la suma convencional de productos parciales, simplemente expresada con brevedad. Para minimizar la cantidad de elementos que se retienen en la memoria, puede ser conveniente realizar primero la suma del producto de multiplicación "cruzada" y luego agregar los otros dos elementos:

{\ Displaystyle (a \ cdot d + b \ cdot c) \ cdot 10}

{\ Displaystyle {} + b \ cdot d}

[de los cuales solo el dígito de las decenas interferirá con el primer término]

{\ Displaystyle {} + a \ cdot c \ cdot 100}

es decir, en este ejemplo

(12 + 14) = 26, 26 × 10 = 260,

al cual es fácil agregar 21: 281 y luego 800: 1081

Un mnemónico fácil de recordar para esto sería FOIL . F significa primero, O significa externo, I significa interno y L significa al final. Por ejemplo:

{\ Displaystyle 75 \ cdot 23}

y

{\ Displaystyle ab \ cdot cd}

donde 7 es a , 5 es b , 2 es c y 3 es d .

Considerar

{\ Displaystyle a \ cdot c \ cdot 100+ (a \ cdot d + b \ cdot c) \ cdot 10 + b \ cdot d}

esta expresión es análoga a cualquier número en base 10 con centenas, decenas y unidades. FOIL también se puede considerar como un número en el que F son las centenas, OI las decenas y L las unidades.

${\ Displaystyle a \ cdot c}$ es el producto del primer dígito de cada uno de los dos números; F.

${\ Displaystyle (a \ cdot d + b \ cdot c)}$ es la suma del producto de los dígitos externos y los internos; OI.

${\ Displaystyle b \ cdot d}$ es el producto del último dígito de cada uno de los dos números; L.

Multiplicar por 2 u otros números pequeños

Cuando un número que se está multiplicando es lo suficientemente pequeño como para multiplicarlo fácilmente por un solo dígito, el producto se puede calcular fácilmente dígito a dígito de derecha a izquierda. Esto es particularmente fácil para multiplicar por 2 ya que el dígito de acarreo no puede ser mayor que 1.

Por ejemplo, para calcular 2 × 167: 2 × 7 = 14, entonces el dígito final es 4 , con un 1 llevado y sumado al 2 × 6 = 12 para dar 13, por lo que el siguiente dígito es 3 con un 1 llevado y sumado al 2 × 1 = 2 para dar 3 . Por tanto, el producto es 334.

Multiplicar por 5

Para multiplicar un número por 5,

1. Primero multiplique ese número por 10, luego divídalo por 2. Los dos pasos son intercambiables, es decir, uno puede dividir el número por la mitad y luego multiplicarlo.

El siguiente algoritmo es una forma rápida de producir este resultado:

2. Agregue un cero al lado derecho del número deseado. (A.) 3. Luego, comenzando desde el número más a la izquierda, divida por 2 (B.) y agregue cada resultado en el orden respectivo para formar un nuevo número (las respuestas fraccionarias deben redondearse hacia abajo al número entero más cercano).

EXAMPLE: Multiply 176 by 5.
     A. Add a zero to 176 to make 1760.
     B. Divide by 2 starting at the left.
           1. Divide 1 by 2 to get .5, rounded down to zero.
           2. Divide 7 by 2 to get 3.5, rounded down to 3.
           3. Divide 6 by 2 to get 3. Zero divided by two is simply zero.

El número resultante es 0330. (Esta no es la respuesta final, sino una primera aproximación que se ajustará en el siguiente paso :)

     C. Add 5 to the number that follows any single numeral
        in this new number that was odd before dividing by two;

EJEMPLO: 176 (EN PRIMER, SEGUNDO TERCER LUGARES):

           1.The FIRST place is 1, which is odd. ADD 5 to the numeral after
             the first place in the new number (0330) which is 3; 3+5=8.
         
           2.The number in the second place of 176, 7, is also odd. The
             corresponding number (0 8 3 0) is increased by 5 as well;
             3+5=8.

           3.The numeral in the third place of 176, 6, is even, therefore
             the final number, zero, in the answer is not changed. That
             final answer is 0880.
             The leftmost zero can be omitted, leaving 880.
             So 176 times 5 equals 880.

EJEMPLO: Multiplica 288 por 5.

A. Dividir 288 entre 2. Uno puede dividir cada dígito individualmente para obtener 144 (dividir un número más pequeño es más fácil).

B. Multiplique por 10. Agregue un cero para obtener el resultado 1440.

Multiplicar por 9

Dado que 9 = 10 - 1, para multiplicar un número por nueve, multiplíquelo por 10 y luego reste el número original del resultado. Por ejemplo, 9 × 27 = 270 - 27 = 243.

Este método se puede ajustar para multiplicar por ocho en lugar de nueve, duplicando el número que se resta; 8 × 27 = 270 - (2 × 27) = 270 - 54 = 216.

De manera similar, al sumar en lugar de restar, se pueden usar los mismos métodos para multiplicar por 11 y 12, respectivamente (aunque existen métodos más simples para multiplicar por 11).

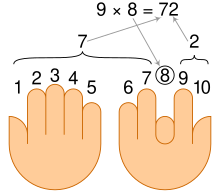
Usando las manos: 1-10 multiplicado por 9

Calcular 9 × 8 con los dedos

Para usar este método, uno debe colocar sus manos frente a ellos, con las palmas hacia ellos. Asigne que el pulgar izquierdo sea 1, el índice izquierdo sea 2, y así sucesivamente hasta el pulgar derecho es diez. Cada "|" simboliza un dedo levantado y un "-" representa un dedo doblado.

1 2 3 4 5  6 7 8 9 10
| | | | |  | | | | |
left hand  right hand

Doble el dedo que representa el número a multiplicar por nueve hacia abajo.

Ej: 6 × 9 sería

| | | | |  − | | | |

El dedo meñique derecho está hacia abajo. Tome el número de dedos que todavía están levantados a la izquierda del dedo doblado y antepóngalo al número de dedos a la derecha.

Ej .: Hay cinco dedos a la izquierda del dedo meñique derecho y cuatro a la derecha del meñique derecho. Entonces 6 × 9 = 54.

    5           4
| | | | |  − | | | |

Multiplicar por 10 (y potencias de diez)

Para multiplicar un número entero por 10, simplemente agregue un 0 adicional al final del número. Para multiplicar un número no entero por 10, mueva el punto decimal un dígito hacia la derecha.

En general, para la base diez, para multiplicar por 10 ⁿ (donde n es un número entero), mueva el punto decimal n dígitos a la derecha. Si n es negativo, mueva el decimal | n | dígitos a la izquierda.

Multiplicar por 11

Para números de un solo dígito, simplemente duplique el número en el dígito de las decenas, por ejemplo: 1 × 11 = 11, 2 × 11 = 22, hasta 9 × 11 = 99.

El producto de cualquier número entero mayor que no sea cero se puede encontrar mediante una serie de adiciones a cada uno de sus dígitos de derecha a izquierda, de dos en dos.

Primero tome el dígito de las unidades y cópielo en el resultado temporal. Luego, comenzando con el dígito de las unidades del multiplicador, agregue cada dígito al dígito a su izquierda. Luego, cada suma se agrega a la izquierda del resultado, delante de todas las demás. Si un número suma 10 o más, tome el dígito de las decenas, que siempre será 1, y transfiéralo a la siguiente suma. Finalmente, copie los multiplicadores del dígito más a la izquierda (valor más alto) al frente del resultado, agregando el 1 llevado si es necesario, para obtener el producto final.

En el caso de un 11 negativo, un multiplicador o ambos, aplique el signo al producto final según la multiplicación normal de los dos números.

Un ejemplo paso a paso de 759 × 11:

El dígito de las unidades del multiplicador, 9, se copia al resultado temporal.
- resultado: 9
Suma 5 + 9 = 14 de modo que 4 se coloque en el lado izquierdo del resultado y lleve el 1.
- resultado: 49
De manera similar, agregue 7 + 5 = 12, luego agregue el 1 transportado para obtener 13. Coloque 3 en el resultado y lleve el 1.
- resultado: 349
Agregue el 1 llevado al dígito de mayor valor en el multiplicador, 7 + 1 = 8, y cópielo al resultado para terminar.
- Producto final de 759 × 11: 8349

Más ejemplos:

−54 × −11 = 5 5 + 4 (9) 4 = 594
999 × 11 = 9 + 1 (10) 9 + 9 + 1 (9) 9 + 9 (8) 9 = 10989
- Tenga en cuenta el manejo de 9 + 1 como el dígito de mayor valor.
−3478 × 11 = 3 3 + 4 + 1 (8) 4 + 7 + 1 (2) 7 + 8 (5) 8 = −38258
62473 × 11 = 6 6 + 2 (8) 2 + 4 + 1 (7) 4 + 7 + 1 (2) 7 + 3 (0) 3 = 687203

Otro método es simplemente multiplicar el número por 10 y agregar el número original al resultado.

Por ejemplo:

17 × 11

     17 × 10 = 170

170 + 17 = 187

17 × 11 = 187.

Una última forma fácil:

Si uno tiene un número de dos dígitos, tómalo y suma los dos números y pon esa suma en el medio, y obtendrás la respuesta.

Por ejemplo: 24 x 11 = 264 porque 2 + 4 = 6 y el 6 se coloca entre el 2 y el 4.

Segundo ejemplo: 87 x 11 = 957 porque 8 + 7 = 15 entonces el 5 va entre el 8 y el 7 y el 1 se lleva al 8. Entonces es básicamente 857 + 100 = 957.

O si 43 x 11 es igual a los primeros 4 + 3 = 7 (para el dígito de las decenas) Entonces 4 es para las centenas y 3 es para las decenas. Y la respuesta es 473

Multiplicar dos números de 2 dígitos entre 11 y 19

Para multiplicar fácilmente números de 2 dígitos entre 11 y 19, un algoritmo simple es el siguiente (donde a es el dígito de las unidades del primer número y b es el dígito de las unidades del segundo número):

(10+a)×(10+b)
100 + 10×(a+b) + a×b

which can be visualized as three parts to be added:

1
xx
 yy

for example:

17×16

1               = 100
13    (7+6)     = 10×(a+b)
 42   (7×6)     = a×b
272   (total)

Usando las manos: 6-10 multiplicado por otro número 6-10

Calculando 9 × 8 y 7 × 6

Esta técnica permite multiplicar un número del 6 al 10 por otro número del 6 al 10.

Asigne 6 al dedo meñique, 7 al dedo anular, 8 al dedo medio, 9 al dedo índice y 10 al pulgar. Toque los dos números deseados juntos. El punto de contacto y la parte inferior se considera la sección "inferior" y todo lo que está por encima de los dos dedos que se tocan forma parte de la sección "superior". La respuesta se forma sumando diez veces el número total de dedos "inferiores" al producto del número de dedos "superiores" de la mano izquierda y la derecha.

Por ejemplo, 9 × 6 se vería así, con el dedo índice izquierdo tocando el dedo meñique derecho:

                               =10==   :right thumb              (top)
                               ==9==   :right index finger       (top)
                               ==8==   :right middle finger      (top)
        left thumb:   =10==    ==7==   :right ring finger        (top)                    
 left index finger:   --9---><---6--   :right little finger      (BOTTOM)  
left middle finger:   --8--                                      (BOTTOM)
  left ring finger:   --7--                                      (BOTTOM)
left little finger:   --6--                                      (BOTTOM)

En este ejemplo, hay 5 dedos "inferiores" (los dedos índice, medio, anular y meñique izquierdo, más el dedo meñique derecho), 1 dedo "superior" izquierdo (el pulgar izquierdo) y 4 dedos "superiores" derechos (el pulgar derecho, el dedo índice, el dedo medio y el dedo anular). Entonces, el cálculo es el siguiente: 9 × 6 = (10 × 5) + (1 × 4) = 54.

Considere otro ejemplo, 8 × 7:

                               =10==   :right thumb              (top)
        left thumb:   =10==    ==9==   :right index finger       (top)
 left index finger:   ==9==    ==8==   :right middle finger      (top)
left middle finger:   --8---><---7--   :right ring finger        (BOTTOM)
  left ring finger:   --7--    --6--   :right little finger      (BOTTOM)
left little finger:   --6--                                      (BOTTOM)

Cinco dedos de abajo hacen 5 decenas, o 50. Dos dedos de arriba a la izquierda y tres dedos de arriba a la derecha hacen el producto 6. Sumar estos produce la respuesta, 56.

Otro ejemplo, esta vez usando 6 × 8:

 --8---><---6--
 --7--
 --6--

Cuatro decenas (abajo), más dos por cuatro (arriba) da 40 + 2 × 4 = 48.

Así es como funciona: cada dedo representa un número entre 6 y 10. Cuando uno se une a los dedos que representan X y Y , habrá 10 - x dedos "top" y x - 5 dedos "fondo" de la mano izquierda; la mano derecha tendrá 10 y dedos "superiores" y y - 5 dedos "inferiores".

Dejar

{\ Displaystyle \, t_ {L} = 10-x \,}

(el número de dedos "superiores" de la mano izquierda)

{\ Displaystyle \, t_ {R} = 10-y \,}

(el número de dedos "superiores" de la mano derecha)

{\ Displaystyle \, b_ {L} = x-5 \,}

(el número de dedos "inferiores" de la mano izquierda)

{\ Displaystyle \, b_ {R} = y-5 \,}

(el número de dedos "inferiores" de la mano derecha)

Luego, siguiendo las instrucciones anteriores se produce

{\ Displaystyle \, 10 (b_ {L} + b_ {R}) + t_ {L} t_ {R}}

{\ Displaystyle \, = 10 [(x-5) + (y-5)] + (10-x) (10-y)}

{\ Displaystyle \, = 10 (x + y-10) + (100-10x-10y + xy)}

{\ Displaystyle \, = [10 (x + y) -100] + [100-10 (x + y) + xy]}

{\ Displaystyle \, = [10 (x + y) -10 (x + y)] + [100-100] + xy}

{\ Displaystyle \, = xy}

cual es el producto deseado.

Multiplicar dos números cercanos y por debajo de 100

Esta técnica permite una fácil multiplicación de números cercanos o inferiores a 100. (90-99) Las variables serán los dos números que uno multiplica.

El producto de dos variables que van del 90 al 99 dará como resultado un número de 4 dígitos. El primer paso es encontrar el dígito de las unidades y el de las decenas.

Reste ambas variables de 100, lo que dará como resultado 2 números de un dígito. El producto de los 2 números de un dígito serán los dos últimos dígitos del producto final.

Luego, reste una de las dos variables de 100. Luego, reste la diferencia de la otra variable. Esa diferencia serán los dos primeros dígitos del producto final, y el número de 4 dígitos resultante será el producto final.

Ejemplo:

          95
        x 97
        ----

Last two digits: 100-95=5 (subtract first number from 100)
                 100-97=3 (subtract second number from 100)
                 5*3=15   (multiply the two differences)
                 Final Product- yx15

First two digits: 100-95=5 (Subtract the first number of the equation from 100)
                  97-5=92  (Subtract that answer from the second number of the equation)
                  Now, the difference will be the first two digits
                  Final Product- 9215

Alternate for first two digits
                  5+3=8    (Add the two single digits derived when calculating "Last two digits" in previous step)
                  100-8=92 (Subtract that answer from 100)
                  Now, the difference will be the first two digits
                  Final Product- 9215

Usando números cuadrados

Los productos de números pequeños se pueden calcular usando los cuadrados de números enteros; por ejemplo, para calcular 13 × 17, se puede observar que 15 es la media de los dos factores y pensar en ello como (15 - 2) × (15 + 2), es decir , 15 ² - 2 ² . Si se sabe que 15 ² es 225 y 2 ² es 4, la resta simple muestra que 225 - 4 = 221, que es el producto deseado.

Este método requiere saber de memoria un cierto número de cuadrados:

1 ² = 1	6 ² = 36	11 ² = 121	16 ² = 256	21 ² = 441	26 ² = 676
2 ² = 4	7 ² = 49	12 ² = 144	17 ² = 289	22 ² = 484	27 ² = 729
3 ² = 9	8 ² = 64	13 ² = 169	18 ² = 324	23 ² = 529	28 ² = 784
4 ² = 16	9 ² = 81	14 ² = 196	19 ² = 361	24 ² = 576	29 ² = 841
5 ² = 25	10 ² = 100	15 ² = 225	20 ² = 400	25 ² = 625	30 ² = 900

Números al cuadrado

Puede resultar útil saber que la diferencia entre dos números cuadrados sucesivos es la suma de sus respectivas raíces cuadradas. Por lo tanto, si uno sabe que 12 × 12 = 144 y desea saber 13 × 13, calcule 144 + 12 + 13 = 169.

Esto se debe a que ( x + 1) ² - x ² = x ² + 2 x + 1 - x ² = x + ( x + 1)

x ² = ( x - 1) ² + (2 x - 1)

Cuadrar cualquier número

Tome un número dado y sume y reste un cierto valor que hará que sea más fácil multiplicar. Por ejemplo:

492 ²

492 está cerca de 500, que es fácil de multiplicar. Suma y resta 8 (la diferencia entre 500 y 492) para obtener

492 -> 484, 500

Multiplica estos números para obtener 242,000 (esto se puede hacer de manera eficiente dividiendo 484 por 2 = 242 y multiplicando por 1000). Finalmente, suma la diferencia (8) al cuadrado (8 ² = 64) al resultado:

492 ² = 242,064

La prueba sigue:

{\ Displaystyle n ^ {2} = n ^ {2}}

{\ Displaystyle n ^ {2} = (n ^ {2} -a ^ {2}) + a ^ {2}}

{\ Displaystyle n ^ {2} = (n ^ {2} -an + an-a ^ {2}) + a ^ {2}}

{\ Displaystyle n ^ {2} = (na) (n + a) + a ^ {2}}

Cuadrar cualquier número entero de 2 dígitos

Este método requiere la memorización de los cuadrados de los números de un dígito del 1 al 9.

El cuadrado de mn , siendo mn un número entero de dos dígitos, se puede calcular como

10 × m ( min + n ) + n ²

Lo que significa que el cuadrado de mn se puede encontrar sumando n a mn , multiplicado por m , sumando 0 al final y finalmente sumando el cuadrado de n .

Por ejemplo, 23 ² :

23 ²

= 10 × 2 (23 + 3) + 3 ²

= 10 × 2 (26) + 9

= 520 + 9

= 529

Entonces 23 ² = 529.

Elevar al cuadrado un número que termina en 5

Tome el dígito (s) que preceden a las cinco: ABC5 , donde a, b, y c son dígitos
Multiplica este número por sí mismo más uno: abc ( abc + 1)
Tome el resultado anterior y agregue 25 al final
- Ejemplo: 85 × 85
  1. 8
  2. 8 × 9 = 72
  3. Entonces, 85 ² = 7,225
- Ejemplo: 125 ²
  1. 12
  2. 12 × 13 = 156.
  3. Entonces, 125 ² = 15,625
- Explicación matemática

(10 x + 5) ²	= (10 x + 5) (10 x + 5)
	= 100 x ² + 100 x + 25
	= 100 ( x ² + x ) + 25
	= 100 x ( x + 1) + 25

Elevar al cuadrado números muy cercanos a 50

Suponga que se necesita elevar al cuadrado un número n cercano a 50.

El número se puede expresar como n = 50 - una por lo que su cuadrado es (50- una ) ² = 50 ² - 100 un + un ² . Uno sabe que 50 ² es 2500. Entonces uno resta 100 a de 2500 y luego suma un ² .

Por ejemplo, digamos que uno quiere elevar al cuadrado 48, que es 50 - 2. Uno resta 200 de 2500 y suma 4, y obtiene n ² = 2304. Para números mayores que 50 ( n = 50 + a ), sume 100 × a en lugar de restarlo.

Elevar al cuadrado un número entero de 26 a 74

Este método requiere la memorización de cuadrados del 1 al 24.

El cuadrado de n (se calcula más fácilmente cuando n está entre 26 y 74 inclusive) es

(50 - n ) ² + 100 ( n - 25)

En otras palabras, el cuadrado de un número es el cuadrado de su diferencia de cincuenta sumado a cien veces la diferencia del número y veinticinco. Por ejemplo, al cuadrado 62:

(−12) ² + [(62-25) × 100]

= 144 + 3.700

= 3.844

Elevar al cuadrado un número entero cerca de 100 (p. Ej., De 76 a 124)

Este método requiere la memorización de cuadrados de 1 a a donde a es la diferencia absoluta entre ny 100. Por ejemplo, los estudiantes que han memorizado sus cuadrados de 1 a 24 pueden aplicar este método a cualquier número entero de 76 a 124.

El cuadrado de n (es decir, 100 ± a ) es

100 (100 ± 2 a ) + a ²

En otras palabras, el cuadrado de un número es el cuadrado de su diferencia de 100 sumado al producto de cien por la diferencia de cien por el producto de dos por la diferencia de cien por el número. Por ejemplo, al cuadrado 93:

100 (100 - 2 (7)) + 7 ²

= 100 × 86 + 49

= 8600 + 49

= 8,649

Otra forma de verlo sería así:

93 ² =? (es −7 de 100)

93 - 7 = 86 (esto da los dos primeros dígitos)

(−7) ² = 49 (estos son los dos segundos dígitos)

93 ² = 8649

Otro ejemplo:

 82² = ?      (is −18 from 100)
 82 − 18 = 64   (subtract.  First digits.)
 (−18)² = 324 (second pair of digits. One will need to carry the 3.)
 82² = 6724

Elevar al cuadrado cualquier número entero cercano a 10 ⁿ (por ejemplo, 976 a 1024, 9976 a 10024, etc.)

Este método es una extensión sencilla de la explicación dada anteriormente para elevar al cuadrado un número entero cercano a 100.

 1012² = ?         (1012 is +12 from 1000)
 (+12)² = 144      (n trailing digits)
 1012 + 12 = 1024  (leading digits)
 1012² = 1024144

 9997² = ?          (9997 is -3 from 10000)
 (-3)² = 0009       (n trailing digits)
 9997 - 3 = 9994    (leading digits)
 9997² = 99940009

Elevar al cuadrado cualquier entero cercano a m × 10 ⁿ (p. Ej., 276 a 324, 4976 a 5024, 79976 a 80024)

Este método es una sencilla extensión de la explicación dada anteriormente para números enteros cercanos a 10 ⁿ .

 407² = ?        (407 is +7 from 400)
 (+7)² = 49      (n trailing digits)
 407 + 7 = 414
 414 × 4 = 1656  (leading digits; note this multiplication by m wasn't needed for integers from 76 to 124 because their m = 1)
 407² = 165649

 79991² = ?          (79991 is -9 from 80000)
 (-9)² = 0081        (n trailing digits)
 79991 - 9
 79982 × 8 = 639856  (leading digits)
 79991² = 6398560081

Encontrar raíces

Aproximación de raíces cuadradas

Una forma fácil de aproximar la raíz cuadrada de un número es usar la siguiente ecuación:

{\ Displaystyle {\ text {raíz}} \ simeq {\ text {raíz cuadrada conocida}} - {\ frac {{\ text {cuadrado conocido}} - {\ text {cuadrado desconocido}}} {2 \ times {\ texto {raíz cuadrada conocida}}}} \,}

Cuanto más cerca esté el cuadrado conocido del desconocido, más precisa será la aproximación. Por ejemplo, para estimar la raíz cuadrada de 15, se podría comenzar con el conocimiento de que el cuadrado perfecto más cercano es 16 (4 ² ).

{\ displaystyle {\ begin {alineado} {\ text {root}} & \ simeq 4 - {\ frac {16-15} {2 \ times 4}} \\ & \ simeq 4-0,125 \\ & \ simeq 3,875 \\\ end {alineado}} \, \!}

Entonces, la raíz cuadrada estimada de 15 es 3.875. La raíz cuadrada real de 15 es 3.872983 ... Una cosa a tener en cuenta es que, sin importar cuál fue la suposición original, la respuesta estimada siempre será mayor que la respuesta real debido a la desigualdad de las medias aritmética y geométrica . Por lo tanto, uno debería intentar redondear la respuesta estimada hacia abajo.

Tenga en cuenta que si n ² es el cuadrado perfecto más cercano al cuadrado deseado x y d = x - n ² es su diferencia, es más conveniente expresar esta aproximación en forma de fracción mixta como . Por lo tanto, en el ejemplo anterior, la raíz cuadrada de 15 es Como otro ejemplo, la raíz cuadrada de 41 es mientras que el valor real es 6.4031 ... ${\ Displaystyle n {\ tfrac {d} {2n}}}$ ${\ displaystyle 4 {\ tfrac {-1} {8}}.}$ ${\ Displaystyle 6 {\ tfrac {5} {12}} = 6.416}$

Derivación

Por definición, si r es la raíz cuadrada de x, entonces

{\ Displaystyle \ mathrm {r} ^ {2} = x \, \!}

Luego se redefine la raíz

{\ Displaystyle \ mathrm {r} = ab \, \!}

donde a es una raíz conocida (4 del ejemplo anterior) yb es la diferencia entre la raíz conocida y la respuesta que se busca.

{\ Displaystyle (ab) ^ {2} = x \, \!}

Expansión de los rendimientos

{\ Displaystyle a ^ {2} -2ab + b ^ {2} = x \, \!}

Si 'a' está cerca del objetivo, 'b' será un número lo suficientemente pequeño como para hacer que el elemento de la ecuación sea insignificante. Por lo tanto, uno puede abandonar y reorganizar la ecuación para ${\ Displaystyle {} + b ^ {2} \,}$ ${\ Displaystyle {} + b ^ {2} \,}$

{\ Displaystyle b \ simeq {\ frac {a ^ {2} -x} {2a}} \, \!}

y por lo tanto

{\ Displaystyle \ mathrm {raíz} \ simeq a - {\ frac {a ^ {2} -x} {2a}} \, \!}

que se puede reducir a

{\ Displaystyle \ mathrm {raíz} \ simeq {\ frac {a ^ {2} + x} {2a}} \, \!}

Extrayendo raíces de poderes perfectos

A menudo se practica la extracción de raíces de poderes perfectos . La dificultad de la tarea no depende del número de dígitos de la potencia perfecta sino de la precisión, es decir, del número de dígitos de la raíz. Además, también depende del orden de la raíz; encontrar raíces perfectas, donde el orden de la raíz es coprime con 10 es algo más fácil ya que los dígitos se mezclan de manera consistente, como en la siguiente sección.

Extraer raíces cúbicas

Una tarea fácil para el principiante es extraer raíces cúbicas de los cubos de números de 2 dígitos. Por ejemplo, dado 74088, determine qué número de dos dígitos, cuando se multiplica por sí mismo una vez y luego se vuelve a multiplicar por el número, da 74088. Quien conoce el método sabrá rápidamente que la respuesta es 42, ya que 42 ³ = 74088.

Antes de aprender el procedimiento, se requiere que el ejecutante memorice los cubos de los números 1-10:

1 ³ = 1	2 ³ = 8	3 ³ = 27	4 ³ = 64	5 ³ = 125
6 ³ = 216	7 ³ = 343	8 ³ = 512	9 ³ = 729	10 ³ = 1000

Observe que hay un patrón en el dígito más a la derecha: sumar y restar con 1 o 3. Empezando desde cero:

0 ³ = 0
1 ³ = 1 hasta 1
2 ³ = 8 abajo 3
3 ³ = 2 7 abajo 1
4 ³ = 6 4 abajo 3
5 ³ = 12 5 arriba 1
6 ³ = 21 6 arriba 1
7 ³ = 34 3 abajo 3
8 ³ = 51 2 abajo 1
9 ³ = 72 9 abajo 3
10 ³ = 100 0 arriba 1

Hay dos pasos para extraer la raíz cúbica del cubo de un número de dos dígitos. Por ejemplo, extrayendo la raíz cúbica de 29791. Determine el lugar de las unidades (unidades) del número de dos dígitos. Dado que el cubo termina en 1, como se ve arriba, debe ser 1.

Si el cubo perfecto termina en 0, su raíz cúbica debe terminar en 0.
Si el cubo perfecto termina en 1, su raíz cúbica debe terminar en 1.
Si el cubo perfecto termina en 2, su raíz cúbica debe terminar en 8.
Si el cubo perfecto termina en 3, su raíz cúbica debe terminar en 7.
Si el cubo perfecto termina en 4, su raíz cúbica debe terminar en 4.
Si el cubo perfecto termina en 5, su raíz cúbica debe terminar en 5.
Si el cubo perfecto termina en 6, su raíz cúbica debe terminar en 6.
Si el cubo perfecto termina en 7, su raíz cúbica debe terminar en 3.
Si el cubo perfecto termina en 8, su raíz cúbica debe terminar en 2.
Si el cubo perfecto termina en 9, su raíz cúbica debe terminar en 9.

Tenga en cuenta que cada dígito se corresponde a sí mismo excepto 2, 3, 7 y 8, que simplemente se restan de diez para obtener el dígito correspondiente.

El segundo paso es determinar el primer dígito de la raíz cúbica de dos dígitos observando la magnitud del cubo dado. Para hacer esto, quite los últimos tres dígitos del cubo dado (29791 → 29) y encuentre el cubo más grande que es mayor (aquí es donde se necesita conocer los cubos de los números 1-10). Aquí, 29 es mayor que 1 al cubo, mayor que 2 al cubo, mayor que 3 al cubo, pero no mayor que 4 al cubo. El cubo más grande es mayor que 3, por lo que el primer dígito del cubo de dos dígitos debe ser 3.

Por lo tanto, la raíz cúbica de 29791 es 31.

Otro ejemplo:

Halla la raíz cúbica de 456533.
La raíz cúbica termina en 7.
Después de quitar los últimos tres dígitos, quedan 456.
456 es mayor que todos los cubos hasta 7 al cubo.
El primer dígito de la raíz cúbica es 7.
La raíz cúbica de 456533 es 77.

Este proceso puede extenderse para encontrar raíces cúbicas que tienen 3 dígitos de longitud, utilizando aritmética módulo 11.

Este tipo de trucos se pueden utilizar en cualquier raíz donde el orden de la raíz sea coprime con 10; por lo tanto, no funciona en raíz cuadrada, ya que la potencia, 2, se divide en 10. 3 no divide 10, por lo tanto, las raíces cúbicas funcionan.

Aproximación de logaritmos comunes (base logarítmica 10)

Para aproximar un logaritmo común (con una precisión de al menos un punto decimal), se requieren algunas reglas de logaritmos y la memorización de algunos logaritmos. Uno debe saber:

log (a × b) = log (a) + log (b)
log (a / b) = log (a) - log (b)
log (0) no existe
log (1) = 0
log (2) ~ .30
log (3) ~ .48
log (7) ~ .85

A partir de esta información, se puede encontrar el logaritmo de cualquier número del 1 al 9.

log (1) = 0
log (2) ~ .30
log (3) ~ .48
log (4) = log (2 × 2) = log (2) + log (2) ~ .60
log (5) = log (10/2) = log (10) - log (2) ~ .70
log (6) = log (2 × 3) = log (2) + log (3) ~ .78
log (7) ~ .85
log (8) = log (2 × 2 × 2) = log (2) + log (2) + log (2) ~ .90
log (9) = log (3 × 3) = log (3) + log (3) ~ .96
log (10) = 1 + log (1) = 1

El primer paso para aproximar el logaritmo común es poner el número dado en notación científica. Por ejemplo, el número 45 en notación científica es 4.5 × 10 ¹ , pero uno lo llamará a × 10 ^b . Luego, encuentre el logaritmo de a, que está entre 1 y 10. Empiece por encontrar el logaritmo de 4, que es .60, y luego el logaritmo de 5, que es .70 porque 4.5 está entre estos dos. A continuación, y la habilidad en esto viene con la práctica, coloque un 5 en una escala logarítmica entre .6 y .7, en algún lugar alrededor de .653 (NOTA: el valor real de los lugares adicionales siempre será mayor que si se colocara en una escala regular. Es decir, uno esperaría que fuera a .650 porque está a la mitad, pero en cambio será un poco más grande, en este caso .653) Una vez que se haya obtenido el logaritmo de a, simplemente agregue b para obtener el aproximación del logaritmo común. En este caso, a + b = .653 + 1 = 1.653. El valor real de log (45) ~ 1,65321.

El mismo proceso se aplica a los números entre 0 y 1. Por ejemplo, 0.045 se escribiría como 4.5 × 10 ⁻² . La única diferencia es que b ahora es negativo, por lo que al sumar uno realmente se resta. Esto produciría el resultado 0,653 - 2 o −1,347.

La aritmética mental como habilidad psicológica

El esfuerzo físico del nivel adecuado puede conducir a un aumento en el desempeño de una tarea mental , como hacer cálculos mentales, realizados posteriormente. Se ha demostrado que durante niveles altos de actividad física hay un efecto negativo en el desempeño de la tarea mental. Esto significa que demasiado trabajo físico puede disminuir la precisión y el rendimiento de los cálculos matemáticos mentales. Se ha demostrado que las medidas fisiológicas , específicamente el EEG , son útiles para indicar la carga de trabajo mental . El uso de un EEG como medida de la carga de trabajo mental después de diferentes niveles de actividad física puede ayudar a determinar el nivel de esfuerzo físico que será más beneficioso para el rendimiento mental. El trabajo anterior realizado en la Universidad Tecnológica de Michigan por Ranjana Mehta incluye un estudio reciente que involucró a participantes que participaron en tareas mentales y físicas concurrentes. Este estudio investigó los efectos de las demandas mentales sobre el rendimiento físico en diferentes niveles de esfuerzo físico y finalmente encontró una disminución en el rendimiento físico cuando las tareas mentales se completaron al mismo tiempo, con un efecto más significativo en el nivel más alto de carga de trabajo físico. El procedimiento de Brown-Peterson es una tarea ampliamente conocida que utiliza aritmética mental. Este procedimiento, que se utiliza principalmente en experimentos cognitivos , sugiere que la resta mental es útil para probar los efectos que el ensayo de mantenimiento puede tener sobre la duración de la memoria a corto plazo .

Campeonato Mundial de Cálculos Mentales

El primer Campeonato Mundial de Cálculos Mentales tuvo lugar en 1997. Este evento se repite todos los años. Consiste en una variedad de tareas diferentes, como la suma de diez números de diez dígitos, la multiplicación de dos números de ocho dígitos, el cálculo de raíces cuadradas, el cálculo de días de la semana para fechas determinadas, el cálculo de raíces cúbicas y algunas tareas misceláneas sorpresa.

Copa del Mundo de Cálculo Mental

El primer Campeonato Mundial de Cálculo Mental ( Copa del Mundo de Cálculo Mental ) tuvo lugar en 2004. Se repiten cada dos años. Consiste en seis tareas diferentes: suma de diez números de diez dígitos, multiplicación de dos números de ocho dígitos, cálculo de raíces cuadradas y cálculo de días de la semana para fechas determinadas, cálculo de raíces cúbicas y algunas tareas misceláneas sorpresa.

Memoriad - Olimpiadas de Memoria Mundial, Cálculo Mental y Lectura Rápida

Memoriad es la primera plataforma que combina concursos de "cálculo mental", "memoria" y "lectura fotográfica". Los juegos y competiciones se llevan a cabo en el año de los Juegos Olímpicos, cada cuatro años. El primer Memoriad se llevó a cabo en Estambul , Turquía , en 2008. El segundo Memoriad tuvo lugar en Antalya , Turquía , del 24 al 25 de noviembre de 2012. Participaron 89 competidores de 20 países. Se entregaron premios y premios en dinero para 10 categorías en total; de las cuales 5 categorías tenían que ver con Cálculo mental (Suma mental, Multiplicación mental, Raíces cuadradas mentales (no enteras), Cálculo de fechas del calendario mental y Flash Anzan).

Ver también

Referencias

enlaces externos

Copa del Mundo de Cálculo Mental
Memoriad - Olimpiadas Mentales Mundiales
Tzourio-Mazoyer, Nathalie; Pesenti, Mauro; Zago, Laure; Crivello, Fabrice; Mellet, Emmanuel; Samson, Dana; Duroux, Bruno; Seron, Xavier; Mazoyer, Bernard (2001). "El cálculo mental en un prodigio se sustenta en áreas temporales prefrontal y medial derecha". Neurociencia de la naturaleza . 4 (1): 103–7. doi : 10.1038 / 82831 . PMID 11135652 . S2CID 23829063 .
Rivera, SM; Reiss, AL; Eckert, MA; Menon, V (2005). "Cambios en el desarrollo de la aritmética mental: evidencia de una mayor especialización funcional en la corteza parietal inferior izquierda" . Corteza cerebral . 15 (11): 1779–90. doi : 10.1093 / cercor / bhi055 . PMID 15716474 .

Languages

In other projects

Cálculo mental - Mental calculation

Métodos y técnicas

Lanzando nueves

Estimacion

Factores

Cálculo de diferencias: a - b

Cálculo directo

Cálculo indirecto

Método de préstamo anticipado

Cálculo de productos: a × b

Multiplicar dos números cualesquiera sumando, restando y enrutando

La fórmula "Fines de cinco"

La fórmula del "prestatario"

Multiplicar cualquier número de 2 dígitos

Multiplicar por 2 u otros números pequeños

Multiplicar por 5

Multiplicar por 9

Usando las manos: 1-10 multiplicado por 9

Multiplicar por 10 (y potencias de diez)

Multiplicar por 11

Multiplicar dos números de 2 dígitos entre 11 y 19

Usando las manos: 6-10 multiplicado por otro número 6-10

Multiplicar dos números cercanos y por debajo de 100

Usando números cuadrados

Números al cuadrado

Cuadrar cualquier número

Cuadrar cualquier número entero de 2 dígitos

Elevar al cuadrado un número que termina en 5

Elevar al cuadrado números muy cercanos a 50

Elevar al cuadrado un número entero de 26 a 74

Elevar al cuadrado un número entero cerca de 100 (p. Ej., De 76 a 124)

Elevar al cuadrado cualquier número entero cercano a 10 n (por ejemplo, 976 a 1024, 9976 a 10024, etc.)

Elevar al cuadrado cualquier entero cercano a m × 10 n (p. Ej., 276 a 324, 4976 a 5024, 79976 a 80024)

Encontrar raíces

Aproximación de raíces cuadradas

Derivación

Extrayendo raíces de poderes perfectos

Extraer raíces cúbicas

Aproximación de logaritmos comunes (base logarítmica 10)

La aritmética mental como habilidad psicológica

Campeonato Mundial de Cálculos Mentales

Copa del Mundo de Cálculo Mental

Memoriad - Olimpiadas de Memoria Mundial, Cálculo Mental y Lectura Rápida

Ver también

Referencias

enlaces externos

Elevar al cuadrado cualquier número entero cercano a 10 ⁿ (por ejemplo, 976 a 1024, 9976 a 10024, etc.)

Elevar al cuadrado cualquier entero cercano a m × 10 ⁿ (p. Ej., 276 a 324, 4976 a 5024, 79976 a 80024)