Modelo matemático para describir la deformación del material bajo tensión.
En la mecánica del continuo , la teoría de deformaciones finitas —también llamada teoría de grandes deformaciones o teoría de grandes deformaciones— se ocupa de deformaciones en las que las deformaciones y / o rotaciones son lo suficientemente grandes como para invalidar los supuestos inherentes a la teoría de deformaciones infinitesimales . En este caso, las configuraciones deformadas y no deformadas del continuo son significativamente diferentes, lo que requiere una clara distinción entre ellas. Este es comúnmente el caso de elastómeros , materiales que se deforman plásticamente y otros fluidos y tejidos blandos biológicos .
Desplazamiento
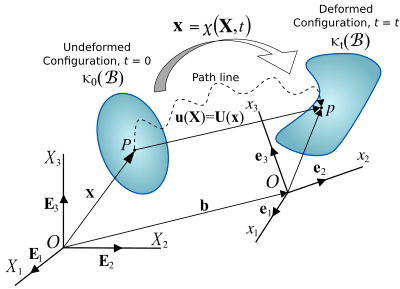
Figura 1. Movimiento de un cuerpo continuo.
El desplazamiento de un cuerpo tiene dos componentes: un desplazamiento de cuerpo rígido y una deformación.
- Un desplazamiento de cuerpo rígido consiste en una traducción simultánea (física) y una rotación del cuerpo sin cambiar su forma o tamaño.
- La deformación implica el cambio de forma y / o tamaño del cuerpo de una configuración inicial o no deformada a una configuración actual o deformada (Figura 1).


Un cambio en la configuración de un cuerpo continuo puede describirse mediante un campo de desplazamiento . Un campo de desplazamiento es un campo vectorial de todos los vectores de desplazamiento para todas las partículas del cuerpo, que relaciona la configuración deformada con la configuración no deformada. La distancia entre dos partículas cualesquiera cambia si y solo si se ha producido una deformación. Si el desplazamiento ocurre sin deformación, entonces es un desplazamiento de cuerpo rígido.
Coordenadas del material (descripción lagrangiana)
El desplazamiento de partículas indexadas por la variable i se puede expresar como sigue. El vector que une las posiciones de una partícula en la configuración no deformada y deformada se llama vector de desplazamiento . Usando en lugar de y en lugar de , los cuales son vectores desde el origen del sistema de coordenadas hasta cada punto respectivo, tenemos la descripción lagrangiana del vector de desplazamiento:







¿Dónde están los vectores unitarios ortonormales que definen la base del sistema de coordenadas espaciales (marco de laboratorio)?

Expresado en términos de las coordenadas del material, el campo de desplazamiento es:

Donde es el vector de desplazamiento que representa la traslación de cuerpo rígido.

La derivada parcial del vector de desplazamiento con respecto a las coordenadas del material produce el tensor del gradiente de desplazamiento del material . Así tenemos,


donde es el tensor del gradiente de deformación .

Coordenadas espaciales (descripción euleriana)
En la descripción euleriana , el vector que se extiende desde una partícula en la configuración no deformada hasta su ubicación en la configuración deformada se llama vector de desplazamiento :


¿Dónde están los vectores unitarios que definen la base del sistema de coordenadas del material (cuerpo-marco)?

Expresado en términos de coordenadas espaciales, el campo de desplazamiento es:

La derivada parcial del vector de desplazamiento con respecto a las coordenadas espaciales produce el tensor de gradiente de desplazamiento espacial . Así tenemos,


Relación entre el material y los sistemas de coordenadas espaciales.
 son los cosenos de dirección entre el material y los sistemas de coordenadas espaciales con vectores unitarios y , respectivamente. Por lo tanto
son los cosenos de dirección entre el material y los sistemas de coordenadas espaciales con vectores unitarios y , respectivamente. Por lo tanto



La relación entre y viene dada por



Sabiendo que

luego

Combinando los sistemas de coordenadas de configuraciones deformadas y no deformadas
Es común superponer los sistemas de coordenadas para las configuraciones deformadas y no deformadas, lo que da como resultado , y los cosenos de dirección se convierten en deltas de Kronecker , es decir


Por lo tanto, en coordenadas materiales (no deformadas), el desplazamiento se puede expresar como:

Y en coordenadas espaciales (deformadas), el desplazamiento se puede expresar como:

Tensor de gradiente de deformación

Figura 2. Deformación de un cuerpo continuo.
El tensor del gradiente de deformación está relacionado tanto con la configuración de referencia como con la actual, como lo ven los vectores unitarios y , por lo tanto, es un tensor de dos puntos .



Debido al supuesto de continuidad de , tiene la inversa , donde es el tensor de gradiente de deformación espacial . Entonces, según el teorema de la función implícita , el determinante jacobiano debe ser no singular , es decir





El tensor de gradiente de deformación del material es un tensor de segundo orden que representa el gradiente de la función de mapeo o relación funcional , que describe el movimiento de un continuo . El tensor de gradiente de deformación del material caracteriza la deformación local en un punto material con vector de posición , es decir, deformación en puntos vecinos, mediante la transformación ( transformación lineal ) de un elemento de línea material que emana de ese punto desde la configuración de referencia a la configuración actual o deformada, asumiendo continuidad. en la función de mapeo , es decir, función diferenciable de y tiempo , lo que implica que las grietas y huecos no se abren ni cierran durante la deformación. Así tenemos,







Vector de desplazamiento relativo
Considere una partícula o un punto de material con un vector de posición en la configuración no deformada (Figura 2). Después de un desplazamiento del cuerpo, la nueva posición de la partícula indicada por en la nueva configuración viene dada por la posición del vector . Los sistemas de coordenadas para la configuración deformada y no deformada se pueden superponer para mayor comodidad.




Considere ahora un punto material vecino , con vector de posición . En la configuración deformada, esta partícula tiene una nueva posición dada por el vector de posición . Suponiendo que los segmentos de línea y que unen las partículas y en la configuración deformada y no deformada, respectivamente, sean muy pequeños, entonces podemos expresarlos como y . Por lo tanto, de la Figura 2 tenemos












donde es el vector de desplazamiento relativo , que representa el desplazamiento relativo de con respecto a en la configuración deformada.



Aproximación de Taylor
Para un elemento infinitesimal , y asumiendo continuidad en el campo de desplazamiento, es posible usar una expansión en serie de Taylor alrededor del punto , despreciando términos de orden superior, para aproximar las componentes del vector de desplazamiento relativo para la partícula vecina como




Por tanto, la ecuación anterior se puede escribir como


Derivado del tiempo del gradiente de deformación
Los cálculos que implican la deformación dependiente del tiempo de un cuerpo a menudo requieren que se calcule una derivada del gradiente de deformación en el tiempo. Una definición geométricamente consistente de tal derivada requiere una excursión a la geometría diferencial, pero evitamos esos problemas en este artículo.
La derivada de tiempo de es

![{\ dot {{\ mathbf {F}}}} = {\ frac {\ parcial {\ mathbf {F}}} {\ parcial t}} = {\ frac {\ parcial} {\ parcial t}} \ izquierda [{\ frac {\ parcial {\ mathbf {x}} ({\ mathbf {X}}, t)} {\ parcial {\ mathbf {X}}}} \ derecha] = {\ frac {\ parcial} { \ parcial {\ mathbf {X}}}} \ izquierda [{\ frac {\ parcial {\ mathbf {x}} ({\ mathbf {X}}, t)} {\ parcial t}} \ derecha] = { \ frac {\ parcial} {\ parcial {\ mathbf {X}}}} \ left [{\ mathbf {V}} ({\ mathbf {X}}, t) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)
donde esta la velocidad. La derivada del lado derecho representa un gradiente de velocidad del material . Es común convertir eso en un gradiente espacial, es decir,

![{\ Displaystyle {\ dot {\ mathbf {F}}} = {\ frac {\ parcial} {\ parcial \ mathbf {X}}} \ left [\ mathbf {V} (\ mathbf {X}, t) \ derecha] = {\ frac {\ parcial} {\ parcial \ mathbf {x}}} \ izquierda [\ mathbf {V} (\ mathbf {X}, t) \ derecha] \ cdot {\ frac {\ parcial \ mathbf {x} (\ mathbf {X}, t)} {\ parcial \ mathbf {X}}} = {\ boldsymbol {l}} \ cdot \ mathbf {F}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eceea87251a369ad9a9d84fe6e37b32801a6241)
donde es el gradiente de velocidad espacial . Si el gradiente de velocidad espacial es constante, la ecuación anterior se puede resolver exactamente para dar


asumiendo en . Hay varios métodos para calcular el exponencial anterior.


Las cantidades relacionadas que se utilizan a menudo en la mecánica del continuo son el tensor de velocidad de deformación y el tensor de giro definidos, respectivamente, como:

El tensor de velocidad de deformación da la velocidad de estiramiento de los elementos lineales, mientras que el tensor de giro indica la velocidad de rotación o vorticidad del movimiento.
La derivada del tiempo material de la inversa del gradiente de deformación (manteniendo fija la configuración de referencia) a menudo se requiere en análisis que involucran deformaciones finitas. Este derivado es

La relación anterior se puede verificar tomando la derivada del tiempo material y notando eso .


Transformación de un elemento de superficie y volumen.
Para transformar cantidades que se definen con respecto a áreas en una configuración deformada a aquellas relativas a áreas en una configuración de referencia, y viceversa, usamos la relación de Nanson, expresada como

donde es un área de una región en la configuración deformada, es la misma área en la configuración de referencia y es la normal hacia afuera al elemento de área en la configuración actual mientras que es la normal hacia afuera en la configuración de referencia, es el gradiente de deformación , y .






La fórmula correspondiente para la transformación del elemento de volumen es

| Derivación de la relación de Nanson (ver también)
|
| Para ver cómo se deriva esta fórmula, comenzamos con los elementos del área orientada
en las configuraciones de referencia y actual:

Los volúmenes de referencia y actuales de un elemento son

donde .

Por lo tanto,

o,

asi que,

Entonces obtenemos

o,

|
Descomposición polar del tensor de gradiente de deformación

Figura 3. Representación de la descomposición polar del gradiente de deformación
El gradiente de deformación , como cualquier tensor de segundo orden invertible, puede descomponerse, utilizando el teorema de descomposición polar , en un producto de dos tensores de segundo orden (Truesdell y Noll, 1965): un tensor ortogonal y un tensor simétrico definido positivo, es decir


donde el tensor es un tensor ortogonal propio , es decir , y , que representa una rotación; el tensor es el tensor de estiramiento derecho ; y el tensor de estiramiento izquierdo . Los términos derecha e izquierda significan que están a la derecha y a la izquierda del tensor de rotación , respectivamente. y son ambos definidos positivos , es decir, y para todos los tensores simétricos y distintos de cero , es decir , y , de segundo orden.













Esta descomposición implica que la deformación de un elemento lineal en la configuración no deformada sobre la configuración deformada, es decir , puede obtenerse bien estirando primero el elemento , es decir , seguido de una rotación , es decir ; o de manera equivalente, aplicando primero una rotación rígida , es decir , seguida más tarde por un estiramiento , es decir (Ver Figura 3).











Debido a la ortogonalidad de 

de modo que y tienen los mismos valores propios o tramos principales , pero diferentes vectores propios o direcciones principales y , respectivamente. Las direcciones principales están relacionadas por





Esta descomposición polar, que es única ya que es invertible con un determinante positivo, es una corrolación de la descomposición en valor singular .

Tensores de deformación
En mecánica se utilizan varios tensores de deformación independientes de la rotación. En mecánica de sólidos, los más populares son los tensores de deformación Cauchy-Green derecho e izquierdo.
Dado que una rotación pura no debe inducir ninguna deformación en un cuerpo deformable, a menudo es conveniente utilizar medidas de deformación independientes de la rotación en la mecánica del continuo . Como una rotación seguida de su rotación inversa no conduce a ningún cambio ( ), podemos excluir la rotación multiplicando por su transposición .


El tensor de deformación de Cauchy-Green derecho
En 1839, George Green introdujo un tensor de deformación conocido como tensor de deformación de Cauchy-Green derecho o tensor de deformación de Green , definido como:

Físicamente, el tensor de Cauchy-Green nos da el cuadrado del cambio local en las distancias debido a la deformación, es decir 
Las invariantes de se utilizan a menudo en las expresiones para las funciones de densidad de energía de deformación . Los invariantes más utilizados son

![{\ begin {alineado} I_ {1} ^ {C} &: = {\ text {tr}} ({\ mathbf {C}}) = C _ {{II}} = \ lambda _ {1} ^ {2 } + \ lambda _ {2} ^ {2} + \ lambda _ {3} ^ {2} \\ I_ {2} ^ {C} &: = {\ tfrac {1} {2}} \ left [( {\ text {tr}} ~ {\ mathbf {C}}) ^ {2} - {\ text {tr}} ({\ mathbf {C}} ^ {2}) \ right] = {\ tfrac {1 } {2}} \ left [(C _ {{JJ}}) ^ {2} -C _ {{IK}} C _ {{KI}} \ right] = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} + \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} + \ lambda _ {3} ^ {2} \ lambda _ {1} ^ {2} \ \ I_ {3} ^ {C} &: = \ det ({\ mathbf {C}}) = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2}. \ End {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/3704e68e2c34682fc7ee876f06e3c89f4197311b)
donde son las relaciones de estiramiento para las fibras unitarias que están inicialmente orientadas a lo largo de las direcciones del vector propio del tensor de estiramiento derecho (referencia) (estos generalmente no están alineados con los tres ejes de los sistemas de coordenadas).

El tensor de deformación del dedo
La IUPAC recomienda que el inverso del tensor de deformación de Cauchy-Green derecho (llamado tensor de Cauchy en ese documento), es decir , se llame tensor de dedo . Sin embargo, esa nomenclatura no se acepta universalmente en la mecánica aplicada.


El tensor de deformación de Cauchy-Green o Finger izquierdo
Invertir el orden de multiplicación en la fórmula para el tensor de deformación de Cauchy-Verde derecho conduce al tensor de deformación de Cauchy-Verde izquierdo que se define como:

El tensor de deformación de Cauchy-Green izquierdo a menudo se denomina tensor de deformación de Finger , que lleva el nombre de Josef Finger (1894).
Las invariantes de también se utilizan en las expresiones para las funciones de densidad de energía de deformación . Los invariantes convencionales se definen como

![{\ begin {alineado} I_ {1} &: = {\ text {tr}} ({\ mathbf {B}}) = B _ {{ii}} = \ lambda _ {1} ^ {2} + \ lambda _ {2} ^ {2} + \ lambda _ {3} ^ {2} \\ I_ {2} &: = {\ tfrac {1} {2}} \ left [({\ text {tr}} ~ {\ mathbf {B}}) ^ {2} - {\ text {tr}} ({\ mathbf {B}} ^ {2}) \ right] = {\ tfrac {1} {2}} \ left ( B _ {{ii}} ^ {2} -B _ {{jk}} B _ {{kj}} \ right) = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} + \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} + \ lambda _ {3} ^ {2} \ lambda _ {1} ^ {2} \\ I_ {3} &: = \ det {\ mathbf {B}} = J ^ {2} = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} \ end {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a3d7bf82330d0d670c9e102fc5cfa569abfbc69)
donde es el determinante del gradiente de deformación.

Para materiales incompresibles, se usa un conjunto de invariantes ligeramente diferente:

El tensor de deformación de Cauchy
A principios de 1828, Augustin Louis Cauchy introdujo un tensor de deformación se define como la inversa de la izquierda tensor de deformación de Cauchy-Green, . Este tensor también se ha llamado tensor de Piola y tensor de dedo en la literatura sobre reología y dinámica de fluidos.


Representación espectral
Si hay tres tramos principales distintos , las descomposiciones espectrales de y viene dada por




Es más,


Observa eso

Por lo tanto, la unicidad de la descomposición espectral también implica eso . El estiramiento izquierdo ( ) también se denomina tensor de estiramiento espacial, mientras que el estiramiento derecho ( ) se denomina tensor de estiramiento del material .



El efecto de actuar es estirar el vector y rotarlo a la nueva orientación , es decir,





En un sentido similar,

| Ejemplos de
|
|
Extensión uniaxial de un material incompresible
Este es el caso en el que una muestra se estira en una dirección con una relación de estiramiento de . Si el volumen permanece constante, la contracción en las otras dos direcciones es tal que o . Luego:
  


Cizalla simple



Rotación rígida del cuerpo


|
Derivadas del estiramiento
Las derivadas del estiramiento con respecto al tensor de deformación de Cauchy-Green derecho se utilizan para derivar las relaciones tensión-deformación de muchos sólidos, particularmente materiales hiperelásticos . Estos derivados son

y seguir de las observaciones que

Interpretación física de los tensores de deformación
Sea un sistema de coordenadas cartesiano definido en el cuerpo deformado y sea otro sistema definido en el cuerpo deformado. Deje que una curva en el cuerpo no deformado se parametrice usando . Su imagen en el cuerpo deformado es .



![s \ in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)

La longitud no deformada de la curva viene dada por

Después de la deformación, la longitud se vuelve
![{\ begin {alineado} l_ {x} & = \ int _ {0} ^ {1} \ left | {\ cfrac {d {\ mathbf {x}}} {ds}} \ right | ~ ds = \ int _ {0} ^ {1} {\ sqrt {{\ cfrac {d {\ mathbf {x}}} {ds}} \ cdot {\ cfrac {d {\ mathbf {x}}} {ds}}}} ~ ds = \ int _ {0} ^ {1} {\ sqrt {\ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ cdot {\ cfrac { d {\ mathbf {X}}} {ds}} \ right) \ cdot \ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ cdot {\ cfrac {d {\ mathbf {X}}} {ds}} \ right)}} ~ ds \\ & = \ int _ {0} ^ {1} {\ sqrt {{\ cfrac {d {\ mathbf {X} " }} {ds}} \ cdot \ left [\ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ right) ^ {T} \ cdot {\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ right] \ cdot {\ cfrac {d {\ mathbf {X}}} {ds}}}} ~ ds \ end { alineado}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)
Tenga en cuenta que el tensor de deformación de Cauchy-Green derecho se define como

Por eso,

lo que indica que los cambios de longitud se caracterizan por .

Tensores de deformación finitos
El concepto de deformación se utiliza para evaluar cuánto difiere localmente un desplazamiento dado de un desplazamiento de cuerpo rígido. Una de esas deformaciones para grandes deformaciones es el tensor de deformación finito de Lagrange , también llamado tensor de deformación Green-Lagrangiano o tensor de deformación Green-St-Venant , definido como

o en función del tensor de gradiente de desplazamiento
![{\ mathbf E} = {\ frac {1} {2}} \ left [(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + \ nabla _ {{{\ mathbf X}}} {\ mathbf u} + (\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} \ cdot \ nabla _ {{{\ mathbf X}}} {\ mathbf u} \ right] \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb57038f53e8acd75c977dd33dc650dd27913b2c)
o

El tensor de deformación verde-lagrangiano es una medida de cuánto difiere de .


El tensor de deformación finita Euleriano-Almansi , referido a la configuración deformada, es decir, descripción euleriana, se define como

o en función de los gradientes de desplazamiento que tenemos

| Derivación de los tensores de deformación finitos lagrangianos y eulerianos
|
Una medida de deformación es la diferencia entre los cuadrados del elemento de línea diferencial , en la configuración no deformada, y en la configuración deformada (Figura 2). Se ha producido una deformación si la diferencia no es cero; de lo contrario, se ha producido un desplazamiento del cuerpo rígido. Así tenemos,
  
En la descripción de Lagrange, utilizando las coordenadas del material como marco de referencia, la transformación lineal entre las líneas diferenciales es

Entonces tenemos,

donde son los componentes de la Cauchy-Green derecha tensor deformación , . Luego, reemplazando esta ecuación en la primera ecuación que tenemos,
 

o

donde , son los componentes de un tensor de segundo orden llamado el tensor de deformación de Green-St-Venant o el tensor de deformación finita de Lagrange ,


En la descripción euleriana, utilizando las coordenadas espaciales como marco de referencia, la transformación lineal entre las líneas diferenciales es

donde son los componentes de la tensor gradiente de deformación espacial , . Así tenemos
 

donde el segundo orden tensor se llama tensor deformación de Cauchy , . Entonces tenemos,
 

o

donde , son los componentes de un tensor de segundo orden llamado tensor de deformación finita de Euleriano-Almansi ,


Tanto los tensores de deformación finitos lagrangianos como los eulerianos pueden expresarse convenientemente en términos del tensor del gradiente de desplazamiento . Para el tensor de deformación de Lagrange, primero diferenciamos el vector de desplazamiento con respecto a las coordenadas del material para obtener el tensor del gradiente de desplazamiento del material ,   

Reemplazando esta ecuación en la expresión para el tensor de deformación finita de Lagrange tenemos
![{\ begin {alineado} {\ mathbf E} & = {\ frac {1} {2}} \ left ({\ mathbf F} ^ {T} {\ mathbf F} - {\ mathbf I} \ right) \ \ & = {\ frac {1} {2}} \ left [\ left \ {(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + {\ mathbf I} \ derecha \} \ izquierda (\ nabla _ {{{\ mathbf X}}} {\ mathbf u} + {\ mathbf I} \ right) - {\ mathbf I} \ right] \\ & = {\ frac {1 } {2}} \ left [(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + \ nabla _ {{{\ mathbf X}}} {\ mathbf u} + (\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} \ cdot \ nabla _ {{{\ mathbf X}}} {\ mathbf u} \ right] \\\ end { alineado}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c63bb3f2bec5cafe7a362ed4734da711ddb0fb)
o
![{\ begin {alineado} E _ {{KL}} & = {\ frac {1} {2}} \ left ({\ frac {\ parcial x_ {j}} {\ parcial X_ {K}}} {\ frac {\ parcial x_ {j}} {\ parcial X_ {L}}} - \ delta _ {{KL}} \ right) \\ & = {\ frac {1} {2}} \ left [\ delta _ { {jM}} \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK}} \ derecha) \ delta _ {{jN}} \ izquierda ( {\ frac {\ parcial U_ {N}} {\ parcial X_ {L}}} + \ delta _ {{NL}} \ derecha) - \ delta _ {{KL}} \ derecha] \\ & = {\ frac {1} {2}} \ izquierda [\ delta _ {{MN}} \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK} } \ derecha) \ izquierda ({\ frac {\ parcial U_ {N}} {\ parcial X_ {L}}} + \ delta _ {{NL}} \ derecha) - \ delta _ {{KL}} \ derecha ] \\ & = {\ frac {1} {2}} \ left [\ left ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK}} \ derecha) \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {L}}} + \ delta _ {{ML}} \ derecha) - \ delta _ {{KL}} \ derecha] \\ & = {\ frac {1} {2}} \ left ({\ frac {\ U_ parcial {K}} {\ X_ parcial {L}}} + {\ frac {\ U_ parcial {L}} { \ parcial X_ {K}}} + {\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} {\ frac {\ parcial U_ {M}} {\ parcial X_ {L}}} \ derecha) \ end {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2191e97fce373db79be4298a1a6769b1ceb97ce)
De manera similar, el tensor de deformación finita de Euleriano-Almansi se puede expresar como

|
Familia Seth-Hill de tensores de deformación generalizados
BR Seth del Instituto Indio de Tecnología Kharagpur fue el primero en demostrar que los tensores de deformación Green y Almansi son casos especiales de una medida de deformación más general . La idea fue ampliada por Rodney Hill en 1968. La familia de medidas de deformación Seth-Hill (también llamadas tensores Doyle-Ericksen) se puede expresar como
![{\ mathbf E} _ {{(m)}} = {\ frac {1} {2m}} ({\ mathbf U} ^ {{2m}} - {\ mathbf I}) = {\ frac {1} {2m}} \ left [{\ mathbf {C}} ^ {{m}} - {\ mathbf {I}} \ right] \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/b56dbd88d4681c3732c87a09d3c96be97d04d651)
Para diferentes valores de tenemos:

![{\ begin {alineado} {\ mathbf E} _ {{(1)}} & = {\ frac {1} {2}} ({\ mathbf U} ^ {{2}} - {\ mathbf I}) = {\ frac {1} {2}} ({\ mathbf {C}} - {\ mathbf {I}}) & \ qquad {\ text {Tensor de cepa verde-lagrangiano}} \\ {\ mathbf E} _ {{(1/2)}} & = ({\ mathbf U} - {\ mathbf I}) = {\ mathbf {C}} ^ {{1/2}} - {\ mathbf {I}} & \ qquad {\ text {Tensor de deformación Biot}} \\ {\ mathbf E} _ {{(0)}} & = \ ln {\ mathbf U} = {\ frac {1} {2}} \, \ ln { \ mathbf {C}} & \ qquad {\ text {Deformación logarítmica, Deformación natural, Deformación verdadera o Deformación Hencky}} \\ {\ mathbf {E}} _ {{(- 1)}} & = {\ frac {1} {2}} \ left [{\ mathbf {I}} - {\ mathbf {U}} ^ {{- 2}} \ right] & \ qquad {\ text {cepa Almansi}} \ end {alineado }} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/02986daeab9d6df911daf7c76fb84647fb5e9024)
La aproximación de segundo orden de estos tensores es

donde es el tensor de deformación infinitesimal.

Son admisibles muchas otras definiciones diferentes de tensores , siempre que todas cumplan las condiciones que:

-
 desaparece para todos los movimientos de cuerpo rígido
desaparece para todos los movimientos de cuerpo rígido
- la dependencia del tensor del gradiente de desplazamiento es continua, continuamente diferenciable y monótona


- También se desea que se reduzca al tensor de deformación infinitesimal como norma



Un ejemplo es el conjunto de tensores

que no pertenecen a la clase Seth-Hill, pero tienen la misma aproximación de segundo orden que las medidas de Seth-Hill en para cualquier valor de .


Relación de estiramiento
La relación de estiramiento es una medida de la deformación normal o extensional de un elemento de línea diferencial, que se puede definir en la configuración deformada o no deformada.
La relación de estiramiento para el elemento diferencial (Figura) en la dirección del vector unitario en el punto material , en la configuración no deformada, se define como




donde es la magnitud deformada del elemento diferencial .


De manera similar, la relación de estiramiento para el elemento diferencial (Figura), en la dirección del vector unitario en el punto material , en la configuración deformada, se define como




La deformación normal en cualquier dirección se puede expresar en función de la relación de estiramiento,



Esta ecuación implica que la deformación normal es cero, es decir, sin deformación, cuando el estiramiento es igual a la unidad. Algunos materiales, como los elastómetros, pueden soportar relaciones de estiramiento de 3 o 4 antes de fallar, mientras que los materiales de ingeniería tradicionales, como el hormigón o el acero, fallan a relaciones de estiramiento mucho más bajas, tal vez del orden de 1,1 (¿referencia?)
Interpretación física del tensor de deformación finito
Los componentes diagonales del tensor de deformación finita de Lagrange están relacionados con la deformación normal, p. Ej.


donde está la deformación normal o deformación de ingeniería en la dirección .


Los componentes fuera de la diagonal del tensor de deformación finita de Lagrange están relacionados con la deformación por cizallamiento, p. Ej.


donde es el cambio en el ángulo entre dos elementos de línea que originalmente eran perpendiculares a las direcciones y , respectivamente.



En determinadas circunstancias, es decir, pequeños desplazamientos y pequeñas tasas de desplazamiento, los componentes del tensor de deformación finita de Lagrange pueden aproximarse por los componentes del tensor de deformación infinitesimal.
| Derivación de la interpretación física de los tensores de deformación finitos lagrangianos y eulerianos
|
La relación de estiramiento para el elemento diferencial (Figura) en la dirección del vector unitario en el punto material , en la configuración no deformada, se define como
   
donde es la magnitud deformada del elemento diferencial .
 
De manera similar, la relación de estiramiento para el elemento diferencial (Figura), en la dirección del vector unitario en el punto material , en la configuración deformada, se define como
  

El cuadrado de la relación de estiramiento se define como

Sabiendo que

tenemos

donde y son vectores unitarios.
 
La deformación normal o deformación de ingeniería en cualquier dirección se puede expresar como una función de la relación de estiramiento,
 

Por lo tanto, la deformación normal en la dirección en el punto del material puede expresarse en términos de la relación de estiramiento como
 

resolviendo porque tenemos


La deformación cortante , o cambio de ángulo entre dos elementos lineales e inicialmente perpendiculares y orientados en las direcciones principales y , respectivamente, también se puede expresar en función de la relación de estiramiento. Desde el producto escalar entre las líneas deformadas y tenemos
     

donde es el ángulo entre las líneas y en la configuración deformada. Definiendo como la deformación cortante o reducción en el ángulo entre dos elementos de línea que originalmente eran perpendiculares, tenemos
   

por lo tanto,

luego

o

|
Tensores de deformación en coordenadas curvilíneas convectivas
Una representación de los tensores de deformación en coordenadas curvilíneas es útil para muchos problemas en la mecánica del continuo, como las teorías de capas no lineales y las grandes deformaciones plásticas. Deje que denotan la función mediante la cual un vector de posición en el espacio se construye a partir de las coordenadas . Se dice que las coordenadas son "convectivas" si corresponden a un mapeo uno a uno hacia y desde partículas lagrangianas en un cuerpo continuo. Si la cuadrícula de coordenadas está "pintada" en el cuerpo en su configuración inicial, entonces esta cuadrícula se deformará y fluirá con el movimiento del material para permanecer pintada en las mismas partículas de material en la configuración deformada de modo que las líneas de la cuadrícula se crucen en la misma partícula de material. en cualquier configuración. El vector tangente a la curva de la línea de cuadrícula de coordenadas deformada en está dado por





Los tres vectores tangentes en forman una base local. Estos vectores están relacionados con los vectores de base recíproca por


Definamos un campo tensorial de segundo orden (también llamado tensor métrico ) con componentes


Los símbolos de Christoffel del primer tipo se pueden expresar como
![\ Gamma _ {{ijk}} = {\ tfrac {1} {2}} [({\ mathbf {g}} _ {i} \ cdot {\ mathbf {g}} _ {k}) _ {{, j}} + ({\ mathbf {g}} _ {j} \ cdot {\ mathbf {g}} _ {k}) _ {{, i}} - ({\ mathbf {g}} _ {i} \ cdot {\ mathbf {g}} _ {j}) _ {{, k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)
Para ver cómo se relacionan los símbolos de Christoffel con el tensor de deformación derecho Cauchy-Green, definamos de manera similar dos bases, la ya mencionada que es tangente a las líneas de cuadrícula deformadas y otra que es tangente a las líneas de cuadrícula no deformadas. A saber,

El gradiente de deformación en coordenadas curvilíneas.
Usando la definición del gradiente de un campo vectorial en coordenadas curvilíneas, el gradiente de deformación se puede escribir como

El tensor de Cauchy-Green derecho en coordenadas curvilíneas
El tensor de deformación de Cauchy-Green derecho está dado por

Si expresamos en términos de componentes con respecto a la base { } tenemos



Por lo tanto,

y el símbolo de Christoffel correspondiente del primer tipo puede escribirse en la siguiente forma.
![\ Gamma _ {{ijk}} = {\ tfrac {1} {2}} [C _ {{ik, j}} + C _ {{jk, i}} - C _ {{ij, k}}] = {\ tfrac {1} {2}} [({\ mathbf {G}} _ {i} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {k}) _ {{, j} } + ({\ mathbf {G}} _ {j} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {k}) _ {{, i}} - ({\ mathbf { G}} _ {i} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {j}) _ {{, k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)
Algunas relaciones entre las medidas de deformación y los símbolos de Christoffel
Considere un mapeo uno a uno de a y supongamos que existen dos campos tensoriales de segundo orden simétricos, definidos positivos y que satisfacen





Luego,

Señalando que

y tenemos


Definir

Por eso

Definir
![[G ^ {{ij}}] = [G _ {{ij}}] ^ {{- 1}} ~; ~~ [g ^ {{\ alpha \ beta}}] = [g _ {{\ alpha \ beta }}] ^ {{- 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)
Luego

Defina los símbolos de Christoffel del segundo tipo como

Luego

Por lo tanto,

La invertibilidad del mapeo implica que

También podemos formular un resultado similar en términos de derivadas con respecto a . Por lo tanto,


Condiciones de compatibilidad
El problema de la compatibilidad en la mecánica del continuo implica la determinación de campos continuos de un solo valor permitidos en los cuerpos. Estas condiciones permisibles dejan el cuerpo sin espacios no físicos o superposiciones después de una deformación. La mayoría de estas condiciones se aplican a cuerpos simplemente conectados. Se requieren condiciones adicionales para los límites internos de múltiples cuerpos conectados.
Compatibilidad del gradiente de deformación
Las condiciones necesarias y suficientes para la existencia de un campo compatible sobre un cuerpo simplemente conectado son


Compatibilidad del tensor de deformación de Cauchy-Green derecho
Las condiciones necesarias y suficientes para la existencia de un campo compatible sobre un cuerpo simplemente conectado son

![R _ {{\ alpha \ beta \ rho}} ^ {\ gamma}: = {\ frac {\ parcial} {\ parcial X ^ {\ rho}}} [\, _ {{(X)}} \ Gamma _ {{\ alpha \ beta}} ^ {\ gamma}] - {\ frac {\ parcial} {\ parcial X ^ {\ beta}}} [\, _ {{(X)}} \ Gamma _ {{\ alpha \ rho}} ^ {\ gamma}] + \, _ {{(X)}} \ Gamma _ {{\ mu \ rho}} ^ {\ gamma} \, _ {{(X)}} \ Gamma _ {{\ alpha \ beta}} ^ {\ mu} - \, _ {{(X)}} \ Gamma _ {{\ mu \ beta}} ^ {\ gamma} \, _ {{(X)} } \ Gamma _ {{\ alpha \ rho}} ^ {\ mu} = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)
Podemos mostrar que estos son los componentes mixtos del tensor de curvatura de Riemann-Christoffel . Por lo tanto, las condiciones necesarias para la compatibilidad son que la curvatura de Riemann-Christoffel de la deformación sea cero.

Compatibilidad del tensor de deformación de Cauchy-Green izquierdo
No se conocen condiciones generales de suficiencia para el tensor de deformación de Cauchy-Green izquierdo en tres dimensiones. Janet Blume ha encontrado condiciones de compatibilidad para campos bidimensionales .

Ver también
Referencias
Otras lecturas
-
Macosko, CW (1994). Reología: principios, medición y aplicaciones . Editores de VCH. ISBN 1-56081-579-5.
enlaces externos






























































![{\ dot {{\ mathbf {F}}}} = {\ frac {\ parcial {\ mathbf {F}}} {\ parcial t}} = {\ frac {\ parcial} {\ parcial t}} \ izquierda [{\ frac {\ parcial {\ mathbf {x}} ({\ mathbf {X}}, t)} {\ parcial {\ mathbf {X}}}} \ derecha] = {\ frac {\ parcial} { \ parcial {\ mathbf {X}}}} \ izquierda [{\ frac {\ parcial {\ mathbf {x}} ({\ mathbf {X}}, t)} {\ parcial t}} \ derecha] = { \ frac {\ parcial} {\ parcial {\ mathbf {X}}}} \ left [{\ mathbf {V}} ({\ mathbf {X}}, t) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2666606a9db3c727de1e94fa372b590683f72c0)

![{\ Displaystyle {\ dot {\ mathbf {F}}} = {\ frac {\ parcial} {\ parcial \ mathbf {X}}} \ left [\ mathbf {V} (\ mathbf {X}, t) \ derecha] = {\ frac {\ parcial} {\ parcial \ mathbf {x}}} \ izquierda [\ mathbf {V} (\ mathbf {X}, t) \ derecha] \ cdot {\ frac {\ parcial \ mathbf {x} (\ mathbf {X}, t)} {\ parcial \ mathbf {X}}} = {\ boldsymbol {l}} \ cdot \ mathbf {F}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7eceea87251a369ad9a9d84fe6e37b32801a6241)

















































![{\ begin {alineado} I_ {1} ^ {C} &: = {\ text {tr}} ({\ mathbf {C}}) = C _ {{II}} = \ lambda _ {1} ^ {2 } + \ lambda _ {2} ^ {2} + \ lambda _ {3} ^ {2} \\ I_ {2} ^ {C} &: = {\ tfrac {1} {2}} \ left [( {\ text {tr}} ~ {\ mathbf {C}}) ^ {2} - {\ text {tr}} ({\ mathbf {C}} ^ {2}) \ right] = {\ tfrac {1 } {2}} \ left [(C _ {{JJ}}) ^ {2} -C _ {{IK}} C _ {{KI}} \ right] = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} + \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} + \ lambda _ {3} ^ {2} \ lambda _ {1} ^ {2} \ \ I_ {3} ^ {C} &: = \ det ({\ mathbf {C}}) = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2}. \ End {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/3704e68e2c34682fc7ee876f06e3c89f4197311b)





![{\ begin {alineado} I_ {1} &: = {\ text {tr}} ({\ mathbf {B}}) = B _ {{ii}} = \ lambda _ {1} ^ {2} + \ lambda _ {2} ^ {2} + \ lambda _ {3} ^ {2} \\ I_ {2} &: = {\ tfrac {1} {2}} \ left [({\ text {tr}} ~ {\ mathbf {B}}) ^ {2} - {\ text {tr}} ({\ mathbf {B}} ^ {2}) \ right] = {\ tfrac {1} {2}} \ left ( B _ {{ii}} ^ {2} -B _ {{jk}} B _ {{kj}} \ right) = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} + \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} + \ lambda _ {3} ^ {2} \ lambda _ {1} ^ {2} \\ I_ {3} &: = \ det {\ mathbf {B}} = J ^ {2} = \ lambda _ {1} ^ {2} \ lambda _ {2} ^ {2} \ lambda _ {3} ^ {2} \ end {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a3d7bf82330d0d670c9e102fc5cfa569abfbc69)


























![s \ in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/aff1a54fbbee4a2677039524a5139e952fa86eb9)


![{\ begin {alineado} l_ {x} & = \ int _ {0} ^ {1} \ left | {\ cfrac {d {\ mathbf {x}}} {ds}} \ right | ~ ds = \ int _ {0} ^ {1} {\ sqrt {{\ cfrac {d {\ mathbf {x}}} {ds}} \ cdot {\ cfrac {d {\ mathbf {x}}} {ds}}}} ~ ds = \ int _ {0} ^ {1} {\ sqrt {\ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ cdot {\ cfrac { d {\ mathbf {X}}} {ds}} \ right) \ cdot \ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ cdot {\ cfrac {d {\ mathbf {X}}} {ds}} \ right)}} ~ ds \\ & = \ int _ {0} ^ {1} {\ sqrt {{\ cfrac {d {\ mathbf {X} " }} {ds}} \ cdot \ left [\ left ({\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ right) ^ {T} \ cdot {\ cfrac {d {\ mathbf {x}}} {d {\ mathbf {X}}}} \ right] \ cdot {\ cfrac {d {\ mathbf {X}}} {ds}}}} ~ ds \ end { alineado}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd1b639bab0e25d96cf46894973e1d2693800d94)




![{\ mathbf E} = {\ frac {1} {2}} \ left [(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + \ nabla _ {{{\ mathbf X}}} {\ mathbf u} + (\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} \ cdot \ nabla _ {{{\ mathbf X}}} {\ mathbf u} \ right] \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb57038f53e8acd75c977dd33dc650dd27913b2c)
























![{\ begin {alineado} {\ mathbf E} & = {\ frac {1} {2}} \ left ({\ mathbf F} ^ {T} {\ mathbf F} - {\ mathbf I} \ right) \ \ & = {\ frac {1} {2}} \ left [\ left \ {(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + {\ mathbf I} \ derecha \} \ izquierda (\ nabla _ {{{\ mathbf X}}} {\ mathbf u} + {\ mathbf I} \ right) - {\ mathbf I} \ right] \\ & = {\ frac {1 } {2}} \ left [(\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} + \ nabla _ {{{\ mathbf X}}} {\ mathbf u} + (\ nabla _ {{{\ mathbf X}}} {\ mathbf u}) ^ {T} \ cdot \ nabla _ {{{\ mathbf X}}} {\ mathbf u} \ right] \\\ end { alineado}}\,\!](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c63bb3f2bec5cafe7a362ed4734da711ddb0fb)
![{\ begin {alineado} E _ {{KL}} & = {\ frac {1} {2}} \ left ({\ frac {\ parcial x_ {j}} {\ parcial X_ {K}}} {\ frac {\ parcial x_ {j}} {\ parcial X_ {L}}} - \ delta _ {{KL}} \ right) \\ & = {\ frac {1} {2}} \ left [\ delta _ { {jM}} \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK}} \ derecha) \ delta _ {{jN}} \ izquierda ( {\ frac {\ parcial U_ {N}} {\ parcial X_ {L}}} + \ delta _ {{NL}} \ derecha) - \ delta _ {{KL}} \ derecha] \\ & = {\ frac {1} {2}} \ izquierda [\ delta _ {{MN}} \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK} } \ derecha) \ izquierda ({\ frac {\ parcial U_ {N}} {\ parcial X_ {L}}} + \ delta _ {{NL}} \ derecha) - \ delta _ {{KL}} \ derecha ] \\ & = {\ frac {1} {2}} \ left [\ left ({\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} + \ delta _ {{MK}} \ derecha) \ izquierda ({\ frac {\ parcial U_ {M}} {\ parcial X_ {L}}} + \ delta _ {{ML}} \ derecha) - \ delta _ {{KL}} \ derecha] \\ & = {\ frac {1} {2}} \ left ({\ frac {\ U_ parcial {K}} {\ X_ parcial {L}}} + {\ frac {\ U_ parcial {L}} { \ parcial X_ {K}}} + {\ frac {\ parcial U_ {M}} {\ parcial X_ {K}}} {\ frac {\ parcial U_ {M}} {\ parcial X_ {L}}} \ derecha) \ end {alineado}} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2191e97fce373db79be4298a1a6769b1ceb97ce)
![{\ mathbf E} _ {{(m)}} = {\ frac {1} {2m}} ({\ mathbf U} ^ {{2m}} - {\ mathbf I}) = {\ frac {1} {2m}} \ left [{\ mathbf {C}} ^ {{m}} - {\ mathbf {I}} \ right] \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/b56dbd88d4681c3732c87a09d3c96be97d04d651)

![{\ begin {alineado} {\ mathbf E} _ {{(1)}} & = {\ frac {1} {2}} ({\ mathbf U} ^ {{2}} - {\ mathbf I}) = {\ frac {1} {2}} ({\ mathbf {C}} - {\ mathbf {I}}) & \ qquad {\ text {Tensor de cepa verde-lagrangiano}} \\ {\ mathbf E} _ {{(1/2)}} & = ({\ mathbf U} - {\ mathbf I}) = {\ mathbf {C}} ^ {{1/2}} - {\ mathbf {I}} & \ qquad {\ text {Tensor de deformación Biot}} \\ {\ mathbf E} _ {{(0)}} & = \ ln {\ mathbf U} = {\ frac {1} {2}} \, \ ln { \ mathbf {C}} & \ qquad {\ text {Deformación logarítmica, Deformación natural, Deformación verdadera o Deformación Hencky}} \\ {\ mathbf {E}} _ {{(- 1)}} & = {\ frac {1} {2}} \ left [{\ mathbf {I}} - {\ mathbf {U}} ^ {{- 2}} \ right] & \ qquad {\ text {cepa Almansi}} \ end {alineado }} \, \!](https://wikimedia.org/api/rest_v1/media/math/render/svg/02986daeab9d6df911daf7c76fb84647fb5e9024)

















































![\ Gamma _ {{ijk}} = {\ tfrac {1} {2}} [({\ mathbf {g}} _ {i} \ cdot {\ mathbf {g}} _ {k}) _ {{, j}} + ({\ mathbf {g}} _ {j} \ cdot {\ mathbf {g}} _ {k}) _ {{, i}} - ({\ mathbf {g}} _ {i} \ cdot {\ mathbf {g}} _ {j}) _ {{, k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c84f52a8b94bf81096fd54ad218ac8c8a794593)






![\ Gamma _ {{ijk}} = {\ tfrac {1} {2}} [C _ {{ik, j}} + C _ {{jk, i}} - C _ {{ij, k}}] = {\ tfrac {1} {2}} [({\ mathbf {G}} _ {i} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {k}) _ {{, j} } + ({\ mathbf {G}} _ {j} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {k}) _ {{, i}} - ({\ mathbf { G}} _ {i} \ cdot {\ boldsymbol {C}} \ cdot {\ mathbf {G}} _ {j}) _ {{, k}}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/626053366fba8dffc9ee988c8728f9b476cee63a)










![[G ^ {{ij}}] = [G _ {{ij}}] ^ {{- 1}} ~; ~~ [g ^ {{\ alpha \ beta}}] = [g _ {{\ alpha \ beta }}] ^ {{- 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6168f5195b650daf063a1dd26b314242926f774)









![R _ {{\ alpha \ beta \ rho}} ^ {\ gamma}: = {\ frac {\ parcial} {\ parcial X ^ {\ rho}}} [\, _ {{(X)}} \ Gamma _ {{\ alpha \ beta}} ^ {\ gamma}] - {\ frac {\ parcial} {\ parcial X ^ {\ beta}}} [\, _ {{(X)}} \ Gamma _ {{\ alpha \ rho}} ^ {\ gamma}] + \, _ {{(X)}} \ Gamma _ {{\ mu \ rho}} ^ {\ gamma} \, _ {{(X)}} \ Gamma _ {{\ alpha \ beta}} ^ {\ mu} - \, _ {{(X)}} \ Gamma _ {{\ mu \ beta}} ^ {\ gamma} \, _ {{(X)} } \ Gamma _ {{\ alpha \ rho}} ^ {\ mu} = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e1d54640569dc6ab58c0fca0c0ab634aef2180)
