Ecuación de Langevin - Langevin equation

En física, una ecuación de Langevin (llamada así por Paul Langevin ) es una ecuación diferencial estocástica que describe la evolución en el tiempo de un subconjunto de grados de libertad. Estos grados de libertad son típicamente variables colectivas (macroscópicas) que cambian solo lentamente en comparación con las otras variables (microscópicas) del sistema. Las variables rápidas (microscópicas) son responsables de la naturaleza estocástica de la ecuación de Langevin. Una aplicación es el movimiento browniano , calculando las estadísticas del movimiento aleatorio de una pequeña partícula en un fluido debido a colisiones con las moléculas circundantes en movimiento térmico.

El movimiento browniano como prototipo

La ecuación de Langevin original describe el movimiento browniano , el movimiento aparentemente aleatorio de una partícula en un fluido debido a colisiones con las moléculas del fluido,

${\ Displaystyle m {\ frac {d \ mathbf {v}} {dt}} = - \ lambda \ mathbf {v} + {\ boldsymbol {\ eta}} \ left (t \ right).}$

Los grados de libertad de interés aquí son la velocidad de la partícula, denota la masa de la partícula. La fuerza que actúa sobre la partícula se escribe como la suma de una fuerza viscosa proporcional a la velocidad de la partícula ( ley de Stokes ) y un término de ruido (el nombre dado en contextos físicos a términos en ecuaciones diferenciales estocásticas que son procesos estocásticos ) que representan la efecto de las colisiones con las moléculas del fluido. La fuerza tiene una distribución de probabilidad gaussiana con función de correlación ${\ Displaystyle \ mathbf {v}}$${\ Displaystyle m}$ ${\ displaystyle {\ boldsymbol {\ eta}} \ left (t \ right)}$${\ displaystyle {\ boldsymbol {\ eta}} \ left (t \ right)}$

${\ Displaystyle \ left \ langle \ eta _ {i} \ left (t \ right) \ eta _ {j} \ left (t ^ {\ prime} \ right) \ right \ rangle = 2 \ lambda k_ {B} T \ delta _ {i, j} \ delta \ left (tt ^ {\ prime} \ right),}$

donde es la constante de Boltzmann , es la temperatura y es el i-ésimo componente del vector . El -Función forma de las correlaciones en los medios de tiempo que la fuerza en un momento se supone que es completamente no correlacionados con la fuerza en cualquier otro momento. Esta es una aproximación; la fuerza aleatoria real tiene un tiempo de correlación distinto de cero que corresponde al tiempo de colisión de las moléculas. Sin embargo, la ecuación de Langevin se usa para describir el movimiento de una partícula "macroscópica" en una escala de tiempo mucho más larga, y en este límite la correlación -y la ecuación de Langevin se vuelven virtualmente exactas. ${\ Displaystyle k_ {B}}$${\ Displaystyle T}$${\ Displaystyle \ eta _ {i} \ left (t \ right)}$${\ displaystyle {\ boldsymbol {\ eta}} \ left (t \ right)}$${\ Displaystyle \ delta}$${\ Displaystyle t}$${\ Displaystyle \ delta}$

Otra característica prototípica de la ecuación de Langevin es la ocurrencia del coeficiente de amortiguamiento en la función de correlación de la fuerza aleatoria, un hecho también conocido como relación de Einstein . ${\ Displaystyle \ lambda}$

Aspectos matemáticos

Una fuerza fluctuante estrictamente correlacionada no es una función en el sentido matemático habitual e incluso la derivada no está definida en este límite. Este problema desaparece cuando la ecuación de Langevin se escribe en forma integral y una ecuación de Langevin siempre debe interpretarse como una abreviatura de su integral de tiempo. El término matemático general para ecuaciones de este tipo es " ecuación diferencial estocástica ". ${\ Displaystyle \ delta}$${\ displaystyle {\ boldsymbol {\ eta}} \ left (t \ right)}$${\ Displaystyle d \ mathbf {v} / dt}$${\ Displaystyle m \ mathbf {v} = \ int ^ {t} \ left (- \ lambda \ mathbf {v} + {\ boldsymbol {\ eta}} \ left (t \ right) \ right) dt,}$

Otra ambigüedad matemática ocurre para las ecuaciones de Langevin (bastante especiales) con un ruido multiplicativo, es decir, términos como en el lado derecho. Tales ecuaciones se pueden interpretar de acuerdo con el esquema de Stratonovich o Ito, y si la derivación de la ecuación de Langevin no dice cuál usar, es cuestionable de todos modos. Consulte el cálculo de Itō . ${\ displaystyle | {\ boldsymbol {v}} (t) | {\ boldsymbol {\ eta}} (t)}$

Ecuación genérica de Langevin

Existe una derivación formal de una ecuación de Langevin genérica a partir de la mecánica clásica. Esta ecuación genérica juega un papel central en la teoría de la dinámica crítica y otras áreas de la mecánica estadística del desequilibrio. La ecuación para el movimiento browniano anterior es un caso especial.

Una condición esencial de la derivación es un criterio que divida los grados de libertad en las categorías lento y rápido. Por ejemplo, el equilibrio termodinámico local en un líquido se alcanza en unos pocos tiempos de colisión. Pero se necesita mucho más tiempo para que las densidades de cantidades conservadas, como la masa y la energía, se relajen hasta el equilibrio. Las densidades de cantidades conservadas, y en particular sus componentes de longitud de onda larga, son por tanto candidatos a variables lentas. Técnicamente, esta división se realiza con el operador de proyección de Zwanzig , la herramienta esencial en la derivación. La derivación no es completamente rigurosa desde la perspectiva de la física matemática porque se basa en ciertas suposiciones plausibles (similares a las suposiciones requeridas en otras partes de la mecánica estadística básica), pero por lo demás es aceptable desde una perspectiva de la física teórica.

Dejar que denotan las variables lentas. La ecuación genérica de Langevin luego dice ${\ Displaystyle A = \ {A_ {i} \}}$

${\ Displaystyle {\ frac {dA_ {i}} {dt}} = k_ {B} T \ sum \ limits _ {j} {\ left [{A_ {i}, A_ {j}} \ right] {\ frac {{d} {\ mathcal {H}}} {dA_ {j}}}} - \ suma \ límites _ {j} {\ lambda _ {i, j} \ left (A \ right) {\ frac { d {\ mathcal {H}}} {dA_ {j}}} +} \ suma \ límites _ {j} {\ frac {d {\ lambda _ {i, j} \ left (A \ right)}} { dA_ {j}}} + \ eta _ {i} \ left (t \ right).}$

La fuerza fluctuante obedece a una distribución de probabilidad gaussiana con función de correlación ${\ Displaystyle \ eta _ {i} \ left (t \ right)}$

${\ Displaystyle \ left \ langle {\ eta _ {i} \ left (t \ right) \ eta _ {j} \ left (t ^ {\ prime} \ right)} \ right \ rangle = 2 \ lambda _ { i, j} \ left (A \ right) \ delta \ left (tt ^ {\ prime} \ right).}$

Esto implica la relación de reciprocidad de Onsager para los coeficientes de amortiguamiento . La dependencia de on es insignificante en la mayoría de los casos. El símbolo denota el hamiltoniano del sistema, donde es la distribución de probabilidad de equilibrio de las variables . Finalmente, es la proyección del corchete de Poisson de las variables lentas y sobre el espacio de las variables lentas. ${\ Displaystyle \ lambda _ {i, j} = \ lambda _ {j, i}}$${\ Displaystyle \ lambda}$${\ Displaystyle d \ lambda _ {i, j} / dA_ {j}}$${\ Displaystyle \ lambda}$${\ Displaystyle A}$${\ Displaystyle {\ mathcal {H}} = - \ ln \ left (p_ {0} \ right)}$${\ Displaystyle p_ {0} \ left (A \ right)}$${\ Displaystyle A}$${\ Displaystyle [A_ {i}, A_ {j}]}$${\ Displaystyle A_ {i}}$${\ Displaystyle A_ {j}}$

En el caso de la moción browniana uno tendría , o y . La ecuación de movimiento para es exacta, no hay fuerza fluctuante ni coeficiente de amortiguación . ${\ Displaystyle {\ mathcal {H}} = \ mathbf {p} ^ {2} / \ left (2mk_ {B} T \ right)}$${\ Displaystyle A = \ {\ mathbf {p} \}}$${\ Displaystyle A = \ {\ mathbf {x}, \ mathbf {p} \}}$${\ Displaystyle [x_ {i}, p_ {j}] = \ delta _ {i, j}}$${\ Displaystyle d \ mathbf {x} / dt = \ mathbf {p} / m}$${\ Displaystyle \ mathbf {x}}$${\ Displaystyle \ eta _ {x}}$${\ Displaystyle \ lambda _ {x, p}}$

Ejemplos de

Ruido térmico en una resistencia eléctrica

Un circuito eléctrico que consta de una resistencia y un condensador.

Existe una estrecha analogía entre la partícula browniana paradigmática discutida anteriormente y el ruido de Johnson , el voltaje eléctrico generado por las fluctuaciones térmicas en cada resistencia. El diagrama de la derecha muestra un circuito eléctrico que consta de una resistencia R y una capacitancia C . La variable lenta es el voltaje U entre los extremos de la resistencia. El hamiltoniano lee , y la ecuación de Langevin se convierte en ${\ Displaystyle {\ mathcal {H}} = E / k_ {B} T = CU ^ {2} / (2k_ {B} T)}$

${\ Displaystyle {\ frac {dU} {dt}} = - {\ frac {U} {RC}} + \ eta \ left (t \ right), \; \; \ left \ langle \ eta \ left (t \ right) \ eta \ left (t ^ {\ prime} \ right) \ right \ rangle = {\ frac {2k_ {B} T} {RC ^ {2}}} \ delta \ left (tt ^ {\ prime }\Derecha).}$

Esta ecuación se puede utilizar para determinar la función de correlación

${\ Displaystyle \ left \ langle U \ left (t \ right) U \ left (t ^ {\ prime} \ right) \ right \ rangle = \ left (k_ {B} T / C \ right) \ exp \ left (- \ left \ vert tt ^ {\ prime} \ right \ vert / RC \ right) \ approx 2Rk_ {B} T \ delta \ left (tt ^ {\ prime} \ right),}$

que se convierte en ruido blanco (ruido de Johnson) cuando la capacitancia C se vuelve insignificante.

Dinámica crítica

La dinámica del parámetro de orden de una transición de fase de segundo orden se ralentiza cerca del punto crítico y se puede describir con una ecuación de Langevin. El caso más simple es la clase de universalidad "modelo A" con un parámetro de orden escalar no conservado, realizado por ejemplo en ferroimanes axiales, ${\ Displaystyle \ varphi}$

${\ Displaystyle {\ begin {alineado} {\ frac {\ parcial \ varphi \ left (\ mathbf {x}, t \ right)} {\ parcial t}} & = - \ lambda {\ frac {\ delta {\ mathcal {H}}} {\ delta \ varphi}} + \ eta \ left (\ mathbf {x}, t \ right), \\ {\ mathcal {H}} & = \ int d ^ {d} x \ izquierda [{\ frac {1} {2}} r_ {0} \ varphi ^ {2} + u \ varphi ^ {4} + {\ frac {1} {2}} (\ nabla \ varphi) ^ {2 } \ right], \\\ left \ langle \ eta \ left (\ mathbf {x}, t \ right) \ eta \ left (\ mathbf {x} ', t' \ right) \ right \ rangle & = 2 \ lambda \ delta \ left (\ mathbf {x} - \ mathbf {x} '\ right) \ delta \ left (t-t' \ right). \ end {alineado}}}$

Otras clases de universalidad (la nomenclatura es "modelo A", ..., "modelo J") contienen un parámetro de orden de difusión, parámetros de orden con varios componentes, otras variables críticas y / o contribuciones de paréntesis de Poisson.

Oscilador armónico en un fluido

${\ Displaystyle m {\ frac {dv} {dt}} = - \ lambda v + \ eta (t) -kx}$

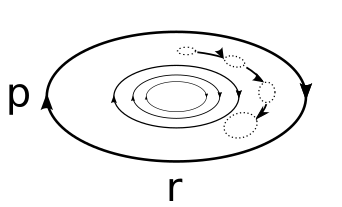
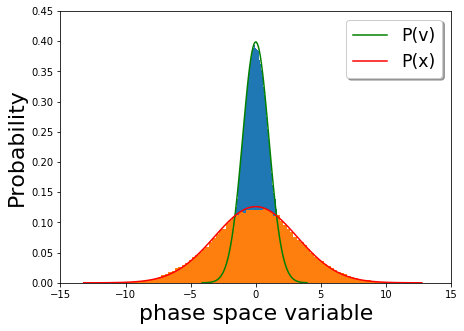
Una partícula en un fluido también se describe mediante la ecuación de Langevin con un potencial, una fuerza de amortiguación y fluctuaciones térmicas dadas por el teorema de fluctuación y disipación . Si el potencial es un potencial de oscilador armónico, entonces las curvas de energía constante son elipses, como se muestra en la Figura 1 a continuación. Sin embargo, en presencia de una fuerza de disipación, una partícula sigue perdiendo energía al medio ambiente. Por otro lado, la fluctuación térmica agrega energía al azar a la partícula. En ausencia de las fluctuaciones térmicas, la partícula pierde continuamente energía cinética y el retrato de fase de la evolución temporal de la velocidad frente a la posición parece una elipse que gira en espiral hasta que alcanza la velocidad cero. Por el contrario, las fluctuaciones térmicas proporcionan patadas a las partículas que no permiten que la partícula pierda toda su energía. Entonces, en tiempos prolongados, el conjunto inicial de osciladores estocásticos se dispersa, llegando finalmente al equilibrio térmico , para quien la distribución de velocidad y posición viene dada por la distribución de Maxwell-Boltzmann . En el gráfico siguiente (Figura 2), la distribución de velocidad a largo plazo (naranja) y las distribuciones de posición (azul) en un potencial armónico ( ) se trazan con las probabilidades de Boltzmann para la velocidad (rojo) y la posición (verde). Vemos que el comportamiento tardío representa el equilibrio térmico. ${\ Displaystyle U = {\ frac {1} {2}} kx ^ {2}}$

Trayectorias de partículas brownianas libres

Considere una partícula libre de masa con ecuación de movimiento descrita por ${\ Displaystyle m}$

${\ Displaystyle m {\ frac {d \ mathbf {v}} {dt}} = - {\ frac {\ mathbf {v}} {\ mu}} + {\ boldsymbol {\ eta}} (t),}$

donde es la velocidad de la partícula, es la movilidad de la partícula, y es una fuerza rápidamente fluctuante cuyo promedio de tiempo se desvanece en una escala de tiempo característica de colisiones de partículas, es decir . La solución general a la ecuación de movimiento es ${\ Displaystyle \ mathbf {v} = d \ mathbf {r} / dt}$${\ Displaystyle \ mu}$${\ Displaystyle {\ boldsymbol {\ eta}} (t) = m \ mathbf {a} (t)}$${\ Displaystyle t_ {c}}$${\ Displaystyle {\ overline {{\ boldsymbol {\ eta}} (t)}} = 0}$

${\ Displaystyle \ mathbf {v} (t) = \ mathbf {v} (0) e ^ {- t / \ tau} + \ int _ {0} ^ {t} \ mathbf {a} (t ') e ^ {- (t-t ') / \ tau} dt',}$

donde es el tiempo de relajación del movimiento browniano. Como se esperaba de la naturaleza aleatoria del movimiento browniano, la velocidad de deriva promedio rápidamente decae a cero en . También se puede demostrar que la función de autocorrelación de la velocidad de la partícula está dada por ${\ Displaystyle \ tau = m \ mu}$${\ Displaystyle \ langle \ mathbf {v} (t) \ rangle = \ mathbf {v} (0) e ^ {- t / \ tau}}$${\ Displaystyle t \ gg \ tau}$${\ Displaystyle \ mathbf {v}}$

Desplazamientos cuadrados simulados de partículas brownianas libres (líneas onduladas semitransparentes) en función del tiempo, para tres opciones seleccionadas de velocidad cuadrada inicial que son 0, 3kT / my 6kT / m respectivamente, siendo 3kT / m el valor de equipartición en equilibrio térmico. Las curvas sólidas coloreadas denotan los desplazamientos cuadrados medios para las opciones de parámetros correspondientes.

${\ Displaystyle {\ begin {alineado} R_ {vv} (t_ {1}, t_ {2}) & \ equiv \ langle \ mathbf {v} (t_ {1}) \ cdot \ mathbf {v} (t_ { 2}) \ rangle \\ & = v ^ {2} (0) e ^ {- (t_ {1} + t_ {2}) / \ tau} + \ int _ {0} ^ {t_ {1}} \ int _ {0} ^ {t_ {2}} R_ {aa} (t_ {1} ', t_ {2}') e ^ {- (t_ {1} + t_ {2} -t_ {1} ' -t_ {2} ') / \ tau} dt_ {1}' dt_ {2} '\\ & \ simeq v ^ {2} (0) e ^ {- | t_ {2} -t_ {1} | / \ tau} + {\ bigg [} {\ frac {3k_ {B} T} {m}} - v ^ {2} (0) {\ bigg]} {\ Big [} e ^ {- | t_ {2 } -t_ {1} | / \ tau} -e ^ {- (t_ {1} + t_ {2}) / \ tau} {\ Big]}, \ end {alineado}}}$

donde hemos utilizado la propiedad de que las variables y no se correlacionan para las separaciones de tiempo . Además, el valor de se establece para que sea igual a tal que obedezca al teorema de equipartición . Tenga en cuenta que si el sistema ya está inicialmente en equilibrio térmico con , entonces para todos , lo que significa que el sistema permanece en equilibrio en todo momento. ${\ Displaystyle \ mathbf {a} (t_ {1} ')}$${\ Displaystyle \ mathbf {a} (t_ {2} ')}$${\ Displaystyle t_ {2} '- t_ {1}' \ gg t_ {c}}$${\ Displaystyle \ lim _ {t \ to \ infty} \ langle v ^ {2} (t) \ rangle = \ lim _ {t \ to \ infty} R_ {vv} (t, t)}$${\ displaystyle 3k_ {B} T / m}$${\ Displaystyle v ^ {2} (0) = 3k_ {B} T / m}$${\ Displaystyle \ langle v ^ {2} (t) \ rangle = 3k_ {B} T / m}$${\ Displaystyle t}$

La velocidad de la partícula browniana se puede integrar para producir su trayectoria (asumiendo que inicialmente está en el origen) ${\ Displaystyle \ mathbf {v} (t)}$

${\ Displaystyle \ mathbf {r} (t) = \ mathbf {v} (0) \ tau {\ big (} 1-e ^ {- t / \ tau} {\ big)} + \ tau \ int _ { 0} ^ {t} \ mathbf {a} (t ') {\ Big [} 1-e ^ {- (t-t') / \ tau} {\ Big]} dt '.}$

Por lo tanto, las asíntotas de desplazamiento promedio resultante a medida que el sistema se relaja y la aleatoriedad se hace cargo. Además, el desplazamiento cuadrático medio se puede determinar de manera similar al cálculo anterior para ser ${\ Displaystyle \ langle \ mathbf {r} (t) \ rangle = \ mathbf {v} (0) \ tau {\ big (} 1-e ^ {- t / \ tau} {\ big)}}$${\ Displaystyle \ mathbf {v} (0) \ tau}$

${\ Displaystyle \ langle r ^ {2} (t) \ rangle = v ^ {2} (0) \ tau ^ {2} {\ big (} 1-e ^ {- t / \ tau} {\ big) } ^ {2} - {\ frac {3k_ {B} T} {m}} \ tau ^ {2} {\ big (} 1-e ^ {- t / \ tau} {\ big)} {\ big (} 3-e ^ {- t / \ tau} {\ big)} + {\ frac {6k_ {B} T} {m}} \ tau t.}$

Puede verse que , lo que indica que el movimiento de las partículas brownianas en escalas de tiempo mucho más cortas que el tiempo de relajación del sistema es (aproximadamente) invariante en la inversión del tiempo . Por otro lado, lo que sugiere que el movimiento aleatorio a largo plazo de las partículas brownianas es un proceso disipativo irreversible . Aquí hemos hecho uso de la relación de Einstein-Smoluchowski , donde es el coeficiente de difusión del fluido. ${\ Displaystyle \ langle r ^ {2} (t \ ll \ tau) \ rangle \ simeq v ^ {2} (0) t ^ {2}}$${\ Displaystyle \ tau}$${\ Displaystyle \ langle r ^ {2} (t \ gg \ tau) \ rangle \ simeq 6k_ {B} T \ tau t / m = 6 \ mu k_ {B} Tt = 6Dt}$ ${\ Displaystyle D = {\ mu \, k_ {B} T}}$${\ Displaystyle D}$

Esta gráfica corresponde a las soluciones de la ecuación de Langevin completa obtenida mediante el método de Euler-Maruyama . El panel de la izquierda muestra la evolución en el tiempo del retrato de fase de un oscilador armónico a diferentes temperaturas. El panel de la derecha captura las distribuciones de probabilidad de equilibrio correspondientes. A temperatura cero, la velocidad decae rápidamente desde su valor inicial (el punto rojo) a cero debido a la amortiguación. Para temperaturas distintas de cero, la velocidad se puede impulsar a valores más altos que el valor inicial debido a fluctuaciones térmicas. En tiempos prolongados, la velocidad permanece distinta de cero y las distribuciones de posición y velocidad corresponden a las del equilibrio térmico.

Recuperando las estadísticas de Boltzmann

Las ecuaciones de Langevin para un sistema en el que cada partícula se ve afectada por una fuerza externa y también colisiones aleatorias con otras partículas deben reproducir la distribución de Boltzmann , que es la función de distribución de probabilidad para partículas en equilibrio térmico. Este es el movimiento browniano en presencia de un forzamiento externo. El caso sobreamortiguado se realiza cuando la inercia de la partícula es despreciable en comparación con la fuerza de amortiguación. La trayectoria de la partícula en un potencial se describe mediante la ecuación de Langevin sobreamortiguada ${\ Displaystyle F = - {\ V parcial / \ X parcial}}$${\ Displaystyle x (t)}$${\ Displaystyle V (x)}$

${\ Displaystyle \ lambda {\ frac {dx} {dt}} = - {\ frac {\ parcial V (x)} {\ parcial x}} + \ eta (t) \ equiv - {\ frac {\ parcial V (x)} {\ parcial x}} + {\ sqrt {2 \ lambda k_ {B} T}} {dB_ {t} \ over dt},}$

donde el ruido se caracteriza por el ruido blanco , o equivalentemente en términos del proceso de Wiener , y es la constante de amortiguación. Nos gustaría calcular la distribución de la posición de la partícula en el transcurso del tiempo. Una forma directa de determinar esta distribución es introducir una función de prueba y observar el promedio de esta función sobre todas las realizaciones (promedio del conjunto) que deberían desaparecer, ${\ Displaystyle \ left \ langle \ eta (t) \ eta (t ') \ right \ rangle = 2k_ {B} T \ lambda \ delta (t-t')}$${\ Displaystyle B_ {t}}$${\ Displaystyle \ lambda}$${\ Displaystyle p (x)}$${\ Displaystyle f}$

${\ Displaystyle {\ frac {d \ left \ langle f (x (t)) \ right \ rangle} {dt}} = 0,}$

porque el promedio de debería ser independiente del tiempo para finito . Ahora, de acuerdo con el lema de Itô para Itô proceso de difusión-deriva X _{t que} satisface la ecuación diferencial estocástica , la diferencial de una función dos veces diferenciable f ( t , x ) está dada por ${\ Displaystyle f (x (t))}$${\ Displaystyle x (t)}$ ${\ Displaystyle dX_ {t} = \ mu _ {t} \, dt + \ sigma _ {t} \, dB_ {t}}$

${\ Displaystyle df = \ left ({\ frac {\ parcial f} {\ parcial t}} + \ mu _ {t} {\ frac {\ parcial f} {\ parcial x}} + {\ frac {\ sigma _ {t} ^ {2}} {2}} {\ frac {\ parcial ^ {2} f} {\ parcial x ^ {2}}} \ derecha) dt + \ sigma _ {t} {\ frac {\ parcial f} {\ parcial x}} \, dB_ {t}.}$

Aplicando esto al cálculo anterior, y considerando que no es una función explícita del tiempo, es decir , se obtiene ${\ Displaystyle f (x (t))}$${\ Displaystyle \ parcial f / \ parcial t = 0}$

${\ Displaystyle \ left \ langle -f '(x) {\ frac {\ parcial V} {\ parcial x}} + k_ {B} Tf' '(x) \ right \ rangle = 0.}$

Este promedio se puede escribir usando la función de densidad de probabilidad ; ${\ Displaystyle p (x)}$

${\ Displaystyle \ int \ left (-f '(x) {\ frac {\ parcial V} {\ parcial x}} p (x) + {k_ {B} T} f' '(x) p (x) \ derecha) dx = \ int \ izquierda (-f '(x) {\ frac {\ parcial V} {\ parcial x}} p (x) - {k_ {B} T} f' (x) p '( x) \ derecha) dx = 0,}$

donde el segundo término estaba integrado por partes (de ahí el signo negativo). Dado que esto es cierto para funciones arbitrarias , debemos tener: ${\ Displaystyle f}$

${\ Displaystyle {\ frac {\ parcial V} {\ parcial x}} p (x) + {k_ {B} T} p '(x) = 0,}$

recuperando así la distribución de Boltzmann

${\ Displaystyle p (x) \ propto \ exp \ left ({- {\ frac {V (x)} {k_ {B} T}}} \ right).}$

Técnicas equivalentes

Una solución de una ecuación de Langevin para una realización particular de la fuerza fluctuante no tiene interés en sí misma; lo que interesa son las funciones de correlación de las variables lentas después de promediar la fuerza fluctuante. Estas funciones de correlación también pueden determinarse con otras técnicas (equivalentes).

Ecuación de Fokker-Planck

Una ecuación de Fokker-Planck es una ecuación determinista para la densidad de probabilidad dependiente del tiempo de las variables estocásticas . La ecuación de Fokker-Planck correspondiente a la ecuación genérica de Langevin anterior puede derivarse con técnicas estándar (ver, por ejemplo, la ref.), ${\ Displaystyle P \ left (A, t \ right)}$${\ Displaystyle A}$

${\ Displaystyle {\ frac {\ parcial P \ izquierda (A, t \ derecha)} {\ parcial t}} = \ suma _ {i, j} {\ frac {\ parcial} {\ parcial A_ {i}} } \ izquierda (-k_ {B} T \ izquierda [A_ {i}, A_ {j} \ derecha] {\ frac {\ parcial {\ mathcal {H}}} {\ parcial A_ {j}}} + \ lambda _ {yo, j} {\ frac {\ parcial {\ mathcal {H}}} {\ parcial A_ {j}}} + \ lambda _ {i, j} {\ frac {\ parcial} {\ parcial A_ {j}}} \ right) P \ left (A, t \ right).}$

La distribución de equilibrio es una solución estacionaria. ${\ Displaystyle P (A) = p_ {0} (A) = {\ text {const}} \ times \ exp (- {\ mathcal {H}})}$

Integral de ruta

Se puede obtener una integral de trayectoria equivalente a una ecuación de Langevin a partir de la ecuación de Fokker-Planck correspondiente o transformando la distribución de probabilidad gaussiana de la fuerza fluctuante en una distribución de probabilidad de las variables lentas, de forma esquemática . El determinante funcional y las sutilezas matemáticas asociadas desaparecen si la ecuación de Langevin se discretiza de forma natural (causal), donde depende de pero no de . Resulta conveniente introducir variables auxiliares de respuesta . La integral de trayectoria equivalente a la ecuación genérica de Langevin luego dice ${\ Displaystyle P ^ {(\ eta)} (\ eta) d \ eta}$${\ Displaystyle \ eta}$${\ Displaystyle P (A) dA = P ^ {(\ eta)} (\ eta (A)) \ det (d \ eta / dA) dA}$${\ Displaystyle A (t + \ Delta t) -A (t)}$${\ Displaystyle A (t)}$${\ Displaystyle A (t + \ Delta t)}$ ${\ Displaystyle {\ tilde {A}}}$

${\ Displaystyle \ int P (A, {\ tilde {A}}) \, dA \, d {\ tilde {A}} = N \ int \ exp \ left (L (A, {\ tilde {A}} ) \ right) dA \, d {\ tilde {A}},}$

donde es un factor de normalización y ${\ Displaystyle N}$

${\ Displaystyle L (A, {\ tilde {A}}) = \ int \ sum _ {i, j} \ left \ {{\ tilde {A}} _ {i} \ lambda _ {i, j} { \ tilde {A}} _ {j} - {\ widetilde {A}} _ {i} \ left \ {\ delta _ {i, j} {\ frac {dA_ {j}} {dt}} - k_ { B} T \ left [A_ {i}, A_ {j} \ right] {\ frac {d {\ mathcal {H}}} {dA_ {j}}} + \ lambda _ {i, j} {\ frac {d {\ mathcal {H}}} {dA_ {j}}} - {\ frac {d \ lambda _ {i, j}} {dA_ {j}}} \ right \} \ right \} dt.}$

La formulación de ruta integral no agrega nada nuevo, pero sí permite el uso de herramientas de la teoría cuántica de campos ; por ejemplo, métodos grupales de perturbación y renormalización (si tienen sentido).

Ver también

• Dinámica de Langevin

Referencias

Otras lecturas

• WT Coffey ( Trinity College, Dublín , Irlanda) y Yu P. Kalmykov ( Universidad de Perpignan , Francia , The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering (tercera edición), World Scientific Series in Contemporary Chemical Physics - Vol 27.
• Reif, F. Fundamentals of Statistical and Thermal Physics , McGraw Hill New York, 1965. Ver sección 15.5 Ecuación de Langevin
• R. Friedrich, J. Peinke y Ch. Renner. Cómo cuantificar las influencias deterministas y aleatorias en las estadísticas del mercado cambiario , Phys. Rev. Lett. 84, 5224 - 5227 (2000)
• LCG Rogers y D. Williams. Difusiones, procesos de Markov y martingalas , Cambridge Mathematical Library, Cambridge University Press, Cambridge, reimpresión de la segunda edición (1994), 2000.