Anatomía computacional - Computational anatomy

La anatomía computacional es un campo interdisciplinario de la biología centrado en la investigación cuantitativa y el modelado de la variabilidad de formas anatómicas. Implica el desarrollo y la aplicación de métodos matemáticos, estadísticos y analíticos de datos para el modelado y simulación de estructuras biológicas.

El campo está ampliamente definido e incluye bases de la anatomía , matemáticas aplicadas y las matemáticas puras , aprendizaje de máquina , mecánica computacional , ciencias de la computación , imágenes biológicas , la neurociencia , la física , la probabilidad y estadísticas ; también tiene fuertes conexiones con la mecánica de fluidos y la mecánica geométrica . Además, complementa campos interdisciplinarios más nuevos, como la bioinformática y la neuroinformática, en el sentido de que su interpretación utiliza metadatos derivados de las modalidades de imágenes de sensor originales (de las cuales la resonancia magnética es un ejemplo). Se centra en las estructuras anatómicas de las que se obtienen imágenes, en lugar de en los dispositivos de imágenes médicas. Es similar en espíritu a la historia de la lingüística computacional , una disciplina que se centra en las estructuras lingüísticas más que en el sensor que actúa como medio de transmisión y comunicación.

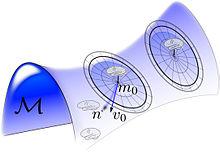
En anatomía computacional, el difeomorfismo grupo se utiliza para diferentes sistemas a través de estudio coordinar transformaciones de coordenadas tal como se genera por medio de las velocidades de Lagrange y de Euler de flujo en . Los flujos entre coordenadas en anatomía computacional están restringidos a ser flujos geodésicos que satisfacen el principio de mínima acción para la energía cinética del flujo . La energía cinética se define mediante una norma de suavidad de Sobolev con estrictamente más de dos derivadas cuadradas integrables generalizadas para cada componente de la velocidad de flujo, lo que garantiza que los flujos de entrada sean difeomorfismos. También implica que la cantidad de movimiento de la forma difeomórfica tomada puntualmente para satisfacer la ecuación de Euler-Lagrange para geodésicas está determinada por sus vecinos a través de derivadas espaciales en el campo de velocidad. Esto separa la disciplina del caso de los fluidos incompresibles para los cuales el momento es una función puntual de la velocidad. La anatomía computacional se cruza con el estudio de las variedades de Riemann y el análisis global no lineal , donde los grupos de difeomorfismos son el foco central. Las teorías emergentes de la forma de alta dimensión son fundamentales para muchos estudios de anatomía computacional, al igual que las preguntas que surgen del incipiente campo de las estadísticas de la forma . Las estructuras métricas en anatomía computacional están relacionadas en espíritu con la morfometría , con la distinción de que la anatomía computacional se enfoca en un espacio de dimensiones infinitas de sistemas de coordenadas transformados por un difeomorfismo , de ahí el uso central de la terminología diffeomorfometría , el estudio espacial métrico de sistemas de coordenadas. vía difeomorfismos. ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ mathbb {R} ^ {3}}$

Génesis

En el corazón de la anatomía computacional está la comparación de formas reconociendo en una forma la otra. Esto conecta a D'Arcy Wentworth Thompson desarrollos 's On Growth and Form lo que ha llevado a las explicaciones científicas de la morfogénesis , el proceso por el cual los patrones se forman en Biología . Los Cuatro libros sobre la proporción humana de Albrecht Durer fueron posiblemente los primeros trabajos sobre anatomía computacional. Los esfuerzos de Noam Chomsky en su pionero de la Lingüística Computacional inspiraron la formulación original de la anatomía computacional como un modelo generativo de forma y forma a partir de ejemplares sobre los que se actuó a través de transformaciones.

Debido a la disponibilidad de mediciones densas en 3D a través de tecnologías como la resonancia magnética (MRI), la anatomía computacional ha surgido como un subcampo de la imagenología médica y la bioingeniería para extraer sistemas de coordenadas anatómicas a escala morfómica en 3D. El espíritu de esta disciplina comparte una fuerte superposición con áreas como la visión por computador y la cinemática de cuerpos rígidos , donde se estudian los objetos analizando los grupos responsables del movimiento en cuestión. La anatomía computacional se aparta de la visión por computadora con su enfoque en movimientos rígidos, ya que el grupo de difeomorfismo de dimensión infinita es fundamental para el análisis de formas biológicas. Es una rama de la escuela de análisis de imágenes y teoría de patrones de la Universidad de Brown, iniciada por Ulf Grenander . En la teoría general de patrones métricos de Grenander , convertir espacios de patrones en un espacio métrico es una de las operaciones fundamentales, ya que poder agrupar y reconocer configuraciones anatómicas a menudo requiere una métrica de formas cercanas y lejanas. La métrica de difeomorfometría de la anatomía computacional mide qué tan lejos están dos cambios difeomórficos de coordenadas entre sí, lo que a su vez induce una métrica en las formas e imágenes indexadas a ellos. Los modelos de la teoría de patrones métricos, en particular la acción grupal en la órbita de formas y formas, es una herramienta central para las definiciones formales en Anatomía Computacional.

Historia

La anatomía computacional es el estudio de la forma y la forma en el morfoma o la anatomía macroscópica milimétrica, o escala de morfología , centrándose en el estudio de subvariedades de puntos, superficies curvas y subvolúmenes de la anatomía humana. Uno de los primeros neuroanatomistas computacionales modernos fue David Van Essen, quien realizó algunos de los primeros desarrollos físicos del cerebro humano basados ​​en la impresión de una corteza humana y cortes. La publicación de Jean Talairach de las coordenadas de Talairach es un hito importante en la escala del morfoma que demuestra la base fundamental de los sistemas de coordenadas locales en el estudio de la neuroanatomía y, por lo tanto, el vínculo claro con los gráficos de geometría diferencial . Al mismo tiempo, el mapeo virtual en anatomía computacional a través de coordenadas de imágenes densas de alta resolución ya estaba ocurriendo en los primeros desarrollos de Ruzena Bajcy y Fred Bookstein basados ​​en tomografía axial computarizada e imágenes de resonancia magnética . La primera introducción del uso de flujos de difeomorfismos para la transformación de sistemas de coordenadas en el análisis de imágenes y la obtención de imágenes médicas fue de Christensen, Joshi, Miller y Rabbitt. ${\ Displaystyle {\ mathbb {R}} ^ {3},}$

La primera formalización de la anatomía computacional como una órbita de plantillas ejemplares bajo la acción grupal de difeomorfismo fue en la conferencia original dada por Grenander y Miller con ese título en mayo de 1997 en el 50 aniversario de la División de Matemáticas Aplicadas en la Universidad de Brown, y la publicación posterior. Esta fue la base de la fuerte desviación de gran parte del trabajo anterior sobre métodos avanzados para la normalización espacial y el registro de imágenes, que históricamente se construyeron sobre las nociones de adición y expansión de bases. La estructura que conserva las transformaciones centrales en el campo moderno de la Anatomía Computacional, los homeomorfismos y difeomorfismos llevan subvariedades suaves sin problemas. Se generan a través de flujos lagrangianos y eulerianos que satisfacen una ley de composición de funciones que forman la propiedad grupal, pero no son aditivos.

El modelo original de anatomía computacional era el triple, el grupo , la órbita de formas y formas , y las leyes de probabilidad que codifican las variaciones de los objetos en la órbita. La plantilla o colección de plantillas son elementos en la órbita de las formas. ${\ Displaystyle ({\ mathcal {G}}, {\ mathcal {M}}, {\ mathcal {P}}) \,}$${\ Displaystyle g \ in {\ mathcal {G}}}$${\ Displaystyle m \ in {\ mathcal {M}}}$${\ Displaystyle P}$${\ Displaystyle m _ {\ mathrm {temp}} \ in {\ mathcal {M}}}$

Las formulaciones lagrangianas y hamiltonianas de las ecuaciones de movimiento de la anatomía computacional despegaron después de 1997 con varias reuniones fundamentales, incluida la reunión Luminy de 1997 organizada por la escuela Azencott en Ecole-Normale Cachan sobre las "Matemáticas del reconocimiento de formas" y el Trimestre de 1998 en el Instituto. Henri Poincar é organizado por David Mumford "Preguntas Mathématiques en Traitement du Signal et de l'Image" que catalizó los grupos Hopkins-Brown-ENS Cachan y los desarrollos posteriores y las conexiones de la anatomía computacional con los desarrollos en el análisis global.

Los desarrollos en anatomía computacional incluyeron el establecimiento de las condiciones de suavidad de Sobelev en la métrica de difeomorfometría para asegurar la existencia de soluciones de problemas variacionales en el espacio de difeomorfismos, la derivación de las ecuaciones de Euler-Lagrange que caracterizan a las geodésicas a través del grupo y las leyes de conservación asociadas, la demostración de las propiedades métricas de la métrica invariante derecha, la demostración de que las ecuaciones de Euler-Lagrange tienen un problema de valor inicial bien planteado con soluciones únicas para todos los tiempos, y con los primeros resultados en curvaturas seccionales para la métrica de difeomorfometría en espacios marcados. Después de la reunión de Los Alamos en 2002, las soluciones originales de Landmark singulares de gran deformación de Joshi en anatomía computacional se conectaron a solitones puntiagudos o Peakons como soluciones para la ecuación Camassa-Holm . Posteriormente, se hicieron conexiones entre las ecuaciones de Euler-Lagrange de anatomía computacional para las densidades de momento para la métrica invariante a la derecha que satisface la suavidad de Sobolev con la caracterización de Vladimir Arnold de la ecuación de Euler para flujos incompresibles que describen geodésicas en el grupo de volumen que conserva difeomorfismos. Han seguido los primeros algoritmos, generalmente denominados LDDMM para mapeo difeomórfico de gran deformación para calcular conexiones entre puntos de referencia en volúmenes y variedades esféricas, curvas, corrientes y superficies, volúmenes, tensores, varices y series de tiempo.

Estas contribuciones de la anatomía computacional al análisis global asociado a las infinitas variedades dimensionales de subgrupos del grupo de difeomorfismos están lejos de ser triviales. La idea original de hacer la geometría diferencial, la curvatura y geodésicas en variedades de dimensión infinita se remonta a Bernhard Riemann 's de habilitación (Ueber die Hypothesen, welche der Geometrie zu Grunde liegen); el libro moderno clave que sienta las bases de tales ideas en el análisis global es de Michor.

Las aplicaciones dentro de las imágenes médicas de la anatomía computacional continuaron floreciendo después de dos reuniones organizadas en las conferencias del Instituto de Matemática Pura y Aplicada en la Universidad de California, Los Ángeles . La anatomía computacional ha sido útil para crear modelos precisos de la atrofia del cerebro humano a escala morfómica, así como plantillas cardíacas, así como para modelar sistemas biológicos. Desde finales de la década de 1990, la anatomía computacional se ha convertido en una parte importante del desarrollo de tecnologías emergentes para el campo de las imágenes médicas. Los atlas digitales son una parte fundamental de la educación de la escuela de medicina moderna y en la investigación de neuroimagen a escala morfómica. Los métodos basados ​​en Atlas y los libros de texto virtuales que se adaptan a variaciones como en las plantillas deformables se encuentran en el centro de muchas plataformas de análisis de neuroimágenes, incluidas Freesurfer, FSL, MRIStudio, SPM. El registro diffeomórfico, introducido en la década de 1990, es ahora un actor importante con bases de códigos existentes organizadas en torno a ANTS, DARTEL, DEMONS, LDDMM, StationaryLDDMM, FastLDDMM, son ejemplos de códigos computacionales utilizados activamente para construir correspondencias entre sistemas de coordenadas basados ​​en características dispersas y densas. imágenes. La morfometría basada en vóxeles es una tecnología importante construida sobre muchos de estos principios.

El modelo de órbita de plantilla deformable de anatomía computacional

El modelo de anatomía humana es una plantilla deformable, una órbita de ejemplares bajo acción grupal. Los modelos de plantilla deformables han sido fundamentales para la teoría de patrones métricos de Grenander, ya que explican la tipicidad a través de plantillas y tienen en cuenta la variabilidad a través de la transformación de la plantilla. Una órbita bajo acción de grupo como representación de la plantilla deformable es una formulación clásica de la geometría diferencial. Se denota el espacio de las formas , con el grupo con ley de composición ; se denota la acción del grupo sobre las formas , donde la acción del grupo se define para satisfacer ${\ Displaystyle m \ in {\ mathcal {M}}}$ ${\ Displaystyle ({\ mathcal {G}}, \ circ)}$${\ Displaystyle \ circ}$${\ Displaystyle g \ cdot m}$${\ Displaystyle g \ cdot m \ in {\ mathcal {M}}, m \ in {\ mathcal {M}}}$

${\ Displaystyle (g \ circ g ^ {\ prime}) \ cdot m = g \ cdot (g ^ {\ prime} \ cdot m) \ in {\ mathcal {M}}.}$

La órbita de la plantilla se convierte en el espacio de todas las formas , siendo homogénea bajo la acción de los elementos de . ${\ Displaystyle {\ mathcal {M}}}$${\ Displaystyle {\ mathcal {M}} \ doteq \ {m = g \ cdot m _ {\ mathrm {temp}}, g \ in {\ mathcal {G}} \}}$${\ Displaystyle {\ mathcal {G}}}$

El modelo de órbita de la anatomía computacional es un álgebra abstracta, que debe compararse con el álgebra lineal , ya que los grupos actúan de forma no lineal sobre las formas. Esta es una generalización de los modelos clásicos de álgebra lineal, en la que el conjunto de vectores de dimensión finita se reemplaza por las subvariedades anatómicas de dimensión finita (puntos, curvas, superficies y volúmenes) y las imágenes de las mismas, y las matrices de álgebra lineal son reemplazado por transformaciones de coordenadas basadas en grupos lineales y afines y los grupos más generales de difeomorfismo de alta dimensión. ${\ Displaystyle {\ mathbb {R}} ^ {n}}$${\ Displaystyle n \ times n}$

Formas y formas

Los objetos centrales son formas o formas en anatomía computacional, un conjunto de ejemplos son las subvariedades de 0,1,2,3 dimensiones de , un segundo conjunto de ejemplos son imágenes generadas a través de imágenes médicas tales como imágenes por resonancia magnética (MRI) y Imagen de resonancia magnética funcional .${\ Displaystyle {\ mathbb {R}} ^ {3}}$

Las variedades de dimensión 0 son puntos de referencia o puntos de referencia; Las variedades unidimensionales son curvas como las curvas sulcul y giratorias en el cerebro; Las variedades bidimensionales corresponden a los límites de las subestructuras en anatomía, como las estructuras subcorticales del mesencéfalo o la superficie giratoria del neocórtex ; los subvolúmenes corresponden a subregiones del cuerpo humano, el corazón , el tálamo , el riñón.

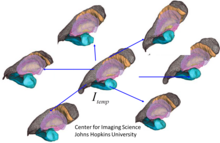
Los puntos de referencia son una colección de puntos sin otra estructura, que delimitan los fiduciales importantes dentro de la forma y la forma humana (ver imagen de puntos de referencia asociados). La sub- colector de formas tales como superficies son colecciones de puntos modelados como parametrizada por un gráfico local o inmersión , (véase la figura que muestra las formas como malla de superficies). Las imágenes, como las imágenes de RM o las imágenes DTI , y las funciones densas son escalares, vectores y matrices (consulte la Figura que muestra la imagen escalar). ${\ Displaystyle X \ doteq \ {x_ {1}, \ dots, x_ {n} \} \ subset {\ mathbb {R}} ^ {3} \ in {\ mathcal {M}}}$${\ Displaystyle X \ subconjunto {\ mathbb {R}} ^ {3} \ in {\ mathcal {M}}}$ ${\ Displaystyle m: U \ subconjunto {\ mathbb {R}} ^ {1,2} \ rightarrow {\ mathbb {R}} ^ {3}}$${\ Displaystyle m (u), u \ en U}$${\ Displaystyle I \ in {\ mathcal {M}}}$${\ Displaystyle I (x), x \ in X \ subset {\ mathbb {R}} ^ {1,2,3}}$

Grupos y acciones grupales

Los grupos y las acciones de grupo están familiarizados con la comunidad de ingenieros con la popularización y estandarización universal del álgebra lineal como modelo básico para analizar señales y sistemas en ingeniería mecánica , ingeniería eléctrica y matemáticas aplicadas . En álgebra lineal, los grupos de matrices (matrices con inversas) son la estructura central, con la acción de grupo definida por la definición habitual de como una matriz, actuando como vectores; la órbita en álgebra lineal es el conjunto de -vectores dado por , que es una acción grupal de las matrices a través de la órbita de . ${\ Displaystyle A}$${\ Displaystyle n \ times n}$${\ Displaystyle x \ in {\ mathbb {R}} ^ {n}}$${\ Displaystyle n \ times 1}$${\ Displaystyle n}$${\ Displaystyle y = A \ cdot x \ in {\ mathbb {R}} ^ {n}}$${\ Displaystyle {\ mathbb {R}} ^ {n}}$

El grupo central en anatomía computacional definido en volúmenes en son los difeomorfismos que son mapeos con 3 componentes , ley de composición de funciones , con inversa . ${\ Displaystyle {\ mathbb {R}} ^ {3}}$ ${\ Displaystyle {\ mathcal {G}} \ doteq Diff}$${\ Displaystyle \ phi (\ cdot) = (\ phi _ {1} (\ cdot), \ phi _ {2} (\ cdot), \ phi _ {3} (\ cdot))}$${\ Displaystyle \ phi \ circ \ phi ^ {\ prime} (\ cdot) \ doteq \ phi (\ phi ^ {\ prime} (\ cdot))}$${\ Displaystyle \ phi \ circ \ phi ^ {- 1} (\ cdot) = \ phi (\ phi ^ {- 1} (\ cdot)) = id}$

Las más populares son las imágenes escalares , con acción a la derecha a través de la inversa. ${\ Displaystyle I (x), x \ in {\ mathbb {R}} ^ {3}}$

${\ Displaystyle \ phi \ cdot I (x) = I \ circ \ phi ^ {- 1} (x), x \ in {\ mathbb {R}} ^ {3}}$.

Para sub- colectores , parametrizados por un gráfico o inmersión , la acción diffeomorfa el flujo de la posición ${\ Displaystyle X \ subconjunto {\ mathbb {R}} ^ {3} \ in {\ mathcal {M}}}$ ${\ Displaystyle m (u), u \ en U}$

${\ Displaystyle \ phi \ cdot m (u) \ doteq \ phi \ circ m (u), u \ in U}$.

Se han definido varias acciones grupales en anatomía computacional .

Flujos lagrangianos y eulerianos para generar difeomorfismos

Para el estudio de la cinemática de cuerpos rígidos , los grupos de Lie de matriz de baja dimensión han sido el foco central. Los grupos de matrices son mapeos de baja dimensión, que son difeomorfismos que proporcionan correspondencias uno a uno entre sistemas de coordenadas, con una inversa suave. El grupo matricial de rotaciones y escalas se puede generar a través de matrices de dimensión finita de forma cerrada que son solución de ecuaciones diferenciales ordinarias simples con soluciones dadas por la matriz exponencial.

Para el estudio de la forma deformable en anatomía computacional, un grupo de difeomorfismo más general ha sido el grupo de elección, que es el análogo de dimensión infinita. Los grupos de diferenciales de alta dimensión utilizados en Anatomía Computacional se generan a través de flujos suaves que satisfacen la especificación Lagrangiana y Euleriana de los campos de flujo como se introdujo por primera vez en., Satisfaciendo la ecuación diferencial ordinaria:${\ Displaystyle \ phi _ {t}, t \ en [0,1]}$

${\ Displaystyle {\ frac {d} {dt}} \ phi _ {t} = v_ {t} \ circ \ phi _ {t}, \ \ phi _ {0} = id \;}$

( Flujo lagrangiano )

con los campos vectoriales en denominada la velocidad euleriana de las partículas en la posición del flujo. Los campos vectoriales son funciones en un espacio funcional, modelado como un espacio de Hilbert suave de alta dimensión, con el jacobiano del flujo como un campo de alta dimensión también en un espacio funcional, en lugar de una matriz de baja dimensión como en la matriz. grupos. Los flujos se introdujeron por primera vez para grandes deformaciones en la coincidencia de imágenes; es la velocidad instantánea de la partícula en el tiempo . ${\ Displaystyle v \ doteq (v_ {1}, v_ {2}, v_ {3})}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ phi}$${\ Displaystyle \ D \ phi \ doteq ({\ frac {\ parcial \ phi _ {i}} {\ parcial x_ {j}}})}$${\ Displaystyle {\ dot {\ phi}} _ {t} (x)}$${\ Displaystyle x}$${\ Displaystyle t}$

La inversa requerida para el grupo se define en el campo vectorial euleriano con flujo inverso advectivo${\ Displaystyle \ phi _ {t} ^ {- 1}, t \ in [0,1]}$

${\ Displaystyle {\ frac {d} {dt}} \ phi _ {t} ^ {- 1} = - (D \ phi _ {t} ^ {- 1}) v_ {t}, \ \ phi _ { 0} ^ {- 1} = id \.}$

( Flujo de transporte inverso )

El grupo de difeomorfismo de anatomía computacional

El grupo de difeomorfismos es muy grande. Para asegurar flujos suaves de difeomorfismos evitando soluciones de choque para la inversa, los campos vectoriales deben ser al menos 1 vez continuamente diferenciables en el espacio. Para los difeomorfismos , los campos vectoriales se modelan como elementos del espacio de Hilbert utilizando los teoremas de incrustación de Sobolev, de modo que cada elemento tiene estrictamente más de 2 derivadas espaciales integrables cuadradas generalizadas (por lo tanto, es suficiente), lo que produce funciones diferenciables continuas de 1 tiempo. ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle (V, \ | \ cdot \ | _ {V})}$${\ Displaystyle v_ {i} \ in H_ {0} ^ {3}, i = 1,2,3,}$

El grupo de difeomorfismos son flujos con campos vectoriales absolutamente integrables en la norma de Sobolev:

${\ Displaystyle Diff_ {V} \ doteq \ {\ varphi = \ phi _ {1}: {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}, \ phi _ {0} = id, \ int _ {0} ^ {1} \ | v_ {t} \ | _ {V} dt <\ infty \} \,}$

( Grupo de difeomorfismo )

donde con el operador lineal mapeando al espacio dual , con la integral calculada por integración por partes cuando es una función generalizada en el espacio dual. ${\ Displaystyle \ | v \ | _ {V} ^ {2} \ doteq \ int _ {X} Av \ cdot vdx, \ v \ in V \,}$${\ Displaystyle A}$${\ Displaystyle A: V \ mapsto V ^ {*}}$${\ Displaystyle Av \ en V ^ {*}}$

Diffeomorfometría: el espacio métrico de formas y formas

El estudio de métricas sobre grupos de difeomorfismos y el estudio de métricas entre variedades y superficies ha sido un área de investigación significativa. La métrica de difeomorfometría mide qué tan cerca y lejos están dos formas o imágenes entre sí; la longitud métrica es la longitud más corta del flujo que lleva un sistema de coordenadas al otro.

A menudo, la métrica euclidiana familiar no es directamente aplicable porque los patrones de formas e imágenes no forman un espacio vectorial. En el modelo de órbita de Riemann de anatomía computacional , los difeomorfismos que actúan sobre las formas no actúan linealmente. Hay muchas formas de definir métricas, y para los conjuntos asociados a formas, la métrica de Hausdorff es otra. El método que usamos para inducir la métrica de Riemann se usa para inducir la métrica en la órbita de las formas definiéndola en términos de la longitud métrica entre las transformaciones del sistema de coordenadas difeomórficas de los flujos. La medición de las longitudes del flujo geodésico entre los sistemas de coordenadas en la órbita de las formas se denomina difeomorfometría . ${\ Displaystyle \ phi \ cdot m \ in {\ mathcal {M}}, \ phi \ in Diff_ {V}, m \ in {\ mathcal {M}}}$

La métrica invariante a la derecha sobre difeomorfismos

Definir la distancia en el grupo de difeomorfismos.

${\ Displaystyle d_ {Diff_ {V}} (\ psi, \ varphi) = \ inf _ {v_ {t}} \ left (\ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dx \ dt: \ phi _ {0} = \ psi, \ phi _ {1} = \ varphi, {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t} \ right) ^ {1/2} \;}$

( difeomorfismos métricos )

esta es la métrica invariante a la derecha de la difeomorfometría, invariante a la reparametrización del espacio ya que para todos , ${\ Displaystyle \ phi \ in Diff_ {V}}$

${\ Displaystyle d_ {Diff_ {V}} (\ psi, \ varphi) = d_ {Diff_ {V}} (\ psi \ circ \ phi, \ varphi \ circ \ phi)}$.

La métrica de formas y formas

La distancia en formas y formas , ${\ Displaystyle d _ {\ mathcal {M}}: {\ mathcal {M}} \ times {\ mathcal {M}} \ rightarrow \ mathbb {R} ^ {+}}$

${\ Displaystyle d _ {\ mathcal {M}} (m, n) = \ inf _ {\ phi \ in \ operatorname {Diff} _ {V}: \ phi \ cdot m = n} d _ {\ operatorname {Diff} _ {V}} (id, \ phi) \;}$

( formas-métricas-formas )

las imágenes se indican con la órbita como una métrica . ${\ Displaystyle I \ in {\ mathcal {I}}}$${\ Displaystyle, d _ {\ mathcal {I}}}$

La integral de acción para el principio de Hamilton sobre flujos difeomórficos

En la mecánica clásica, la evolución de los sistemas físicos se describe mediante soluciones a las ecuaciones de Euler-Lagrange asociadas al principio de mínima acción de Hamilton . Esta es una forma estándar, por ejemplo, de obtener las leyes de movimiento de partículas libres de Newton . De manera más general, las ecuaciones de Euler-Lagrange se pueden derivar para sistemas de coordenadas generalizadas . La ecuación de Euler-Lagrange en anatomía computacional describe los flujos geodésicos de trayectoria más corta entre sistemas de coordenadas de la métrica de difeomorfismo. En anatomía computacional las coordenadas generalizadas son el flujo del difeomorfismo y su velocidad lagrangiana , los dos relacionados a través de la velocidad euleriana . El principio de Hamilton para generar la ecuación de Euler-Lagrange requiere la acción integral en el Lagrangiano dada por ${\ Displaystyle \ phi, {\ dot {\ phi}}}$${\ Displaystyle v \ doteq {\ dot {\ phi}} \ circ \ phi ^ {- 1}}$

${\ Displaystyle J (\ phi) \ doteq \ int _ {0} ^ {1} L (\ phi _ {t}, {\ dot {\ phi}} _ {t}) dt \;}$

( Hamiltoniano-Integrado-Lagrangiano )

el lagrangiano está dado por la energía cinética:

${\ Displaystyle L (\ phi _ {t}, {\ dot {\ phi}} _ {t}) \ doteq {\ frac {1} {2}} \ int _ {X} A ({\ dot {\ phi}} _ {t} \ circ \ phi _ {t} ^ {- 1}) \ cdot ({\ dot {\ phi}} _ {t} \ circ \ phi _ {t} ^ {- 1}) dx = {\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} \ dx \.}$

( Energía cinética lagrangiana )

Momento de forma diffeomórfica o euleriana

En anatomía computacional, primero se llamó el momento de forma euleriana o difeomórfica ya que cuando se integra contra la velocidad euleriana da densidad de energía, y dado que hay una conservación del momento de forma difeomórfica que se mantiene. El operador es el momento de inercia generalizado u operador de inercia. ${\ displaystyle Av}$${\ Displaystyle v}$${\ Displaystyle A}$

La ecuación de Euler-Lagrange sobre el momento de forma para geodésicas en el grupo de difeomorfismos

El cálculo clásico de la ecuación de Euler-Lagrange a partir del principio de Hamilton requiere la perturbación del Lagrangiano en el campo vectorial en la energía cinética con respecto a la perturbación de primer orden del flujo. Esto requiere un ajuste por el corchete de Lie del campo vectorial , dado por el operador que involucra el jacobiano dado por ${\ Displaystyle ad_ {v}: w \ in V \ mapsto V}$

${\ Displaystyle ad_ {v} [w] \ doteq [v, w] \ doteq (Dv) w- (Dw) v \ in V}$.

Al definir el adjunto , la variación de primer orden da el impulso de la forma euleriana que satisface la ecuación generalizada: ${\ Displaystyle ad_ {v} ^ {*}: V ^ {*} \ rightarrow V ^ {*},}$${\ Displaystyle Av \ en V ^ {*}}$

${\ Displaystyle {\ frac {d} {dt}} Av_ {t} + ad_ {v_ {t}} ^ {*} (Av_ {t}) = 0 \, \ t \ en [0,1] \; }$

( EL-General )

significado para todo suave ${\ Displaystyle w \ en V,}$

${\ Displaystyle \ int _ {X} \ left ({\ frac {d} {dt}} Av_ {t} + ad_ {v_ {t}} ^ {*} (Av_ {t}) \ right) \ cdot wdx = \ int _ {X} {\ frac {d} {dt}} Av_ {t} \ cdot wdx + \ int _ {X} Av_ {t} \ cdot ((Dv_ {t}) w- (Dw) v_ { t}) dx = 0.}$

La anatomía computacional es el estudio de los movimientos de subvariedades, puntos, curvas, superficies y volúmenes. La cantidad de movimiento asociada a puntos, curvas y superficies son todas singulares, lo que implica que la cantidad de movimiento se concentra en subconjuntos de los cuales son dimensiones en la medida de Lebesgue . En tales casos, la energía aún está bien definida ya que aunque es una función generalizada, los campos vectoriales son suaves y el impulso euleriano se entiende a través de su acción sobre funciones suaves. La ilustración perfecta de esto es que incluso cuando se trata de una superposición de delta-diracs, la velocidad de las coordenadas en todo el volumen se mueve suavemente. La ecuación de Euler-Lagrange ( EL-General ) sobre difeomorfismos para funciones generalizadas se derivó en. En Riemannian Metric and Lie-Bracket Interpretation of the Euler-Lagrange Equation on Geodesics derivaciones se proporcionan en términos del operador adjunto y el corchete de Lie para el grupo de difeomorfismos. Se le ha dado el nombre de ecuación EPDiff para difeomorfismos que se conectan al método de Euler-Poincare después de haber sido estudiado en el contexto del operador inercial para fluidos incompresibles, libres de divergencia. ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ leq 2}$${\ Displaystyle (Av_ {t} \ mid v_ {t})}$${\ Displaystyle Av_ {t}}$${\ Displaystyle Av \ en V ^ {*}}$${\ displaystyle A = identidad}$

Momento de forma difeomórfica: una función vectorial clásica

Para el caso de la densidad de momento , la ecuación de Euler-Lagrange tiene una solución clásica:${\ Displaystyle (Av_ {t} \ mid w) = \ int _ {X} \ mu _ {t} \ cdot w \, dx}$

${\ Displaystyle {\ frac {d} {dt}} \ mu _ {t} + (Dv_ {t}) ^ {T} \ mu _ {t} + (D \ mu _ {t}) v_ {t} + (\ nabla \ cdot v) \ mu _ {t} = 0 \, t \ in [0,1].}$

( EL-Clásico )

La ecuación de Euler-Lagrange sobre difeomorfismos, definida clásicamente para densidades de momento, apareció por primera vez para el análisis de imágenes médicas.

Exponencial de Riemann (posicionamiento geodésico) y logaritmo de Riemann (coordenadas geodésicas)

En la imagenología médica y la anatomía computacional, el posicionamiento y la coordinación de formas son operaciones fundamentales; el sistema para posicionar coordenadas anatómicas y formas construido sobre la métrica y la ecuación de Euler-Lagrange, un sistema de posicionamiento geodésico como se explicó por primera vez en Miller Trouve y Younes. Resolver la geodésica a partir de la condición inicial se denomina exponencial de Riemann, un mapeo en la identidad del grupo. ${\ Displaystyle v_ {0}}$${\ Displaystyle Exp _ {\ rm {id}} (\ cdot): V \ to Diff_ {V}}$

La exponencial de Riemann satisface la condición inicial , dinámica de campo vectorial , ${\ Displaystyle Exp_ {id} (v_ {0}) = \ phi _ {1}}$${\ Displaystyle {\ dot {\ phi}} _ {0} = v_ {0}}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}, t \ in [0,1]}$

• para clásica ecuación difeomorfa impulso forma , y, a continuación${\ Displaystyle \ int _ {X} Av_ {t} \ cdot w \, dx}$${\ Displaystyle Av \ in V}$

${\ Displaystyle \ \ \ {\ frac {d} {dt}} Av_ {t} + (Dv_ {t}) ^ {T} Av_ {t} + (DAv_ {t}) v_ {t} + (\ nabla \ cdot v) Av_ {t} = 0 \;}$

• para la ecuación generalizada, a continuación , ,${\ Displaystyle Av \ en V ^ {*}}$${\ Displaystyle w \ in V}$

${\ Displaystyle \ \ \ \ int _ {X} {\ frac {d} {dt}} Av_ {t} \ cdot wdx + \ int _ {X} Av_ {t} \ cdot ((Dv_ {t}) w- (Dw) v_ {t}) dx = 0.}$

Calcular el flujo en el logaritmo riemanniano de coordenadas , mapear en la identidad desde el campo vectorial ; ${\ Displaystyle v_ {0}}$${\ Displaystyle Log _ {\ rm {id}} (\ cdot): Diff_ {V} \ to V}$${\ Displaystyle \ varphi}$${\ Displaystyle v_ {0} \ in V}$

${\ displaystyle Log_ {id} (\ varphi) = v_ {0} \ {\ text {condición inicial de EL geodesic}} {\ dot {\ phi}} _ {0} = v_ {0}, \ phi _ { 0} = id, \ phi _ {1} = \ varphi \.}$

Extendido a todo el grupo en el que se convierten

${\ Displaystyle \ phi = Exp _ {\ varphi} (v_ {0} \ circ \ varphi) \ doteq Exp_ {id} (v_ {0}) \ circ \ varphi}$ ; . ${\ Displaystyle Log _ {\ varphi} (\ phi) \ doteq Log_ {id} (\ phi \ circ \ varphi ^ {- 1}) \ circ \ varphi}$

Estos son inversos entre sí para soluciones únicas de logaritmo; el primero se llama posicionamiento geodésico, el segundo coordenadas geodésicas (ver mapa exponencial, geometría de Riemann para la versión de dimensión finita). La métrica geodésica es un aplanamiento local del sistema de coordenadas de Riemann (ver figura).

Formulación hamiltoniana de anatomía computacional

En anatomía computacional, los difeomorfismos se utilizan para impulsar los sistemas de coordenadas, y los campos vectoriales se utilizan como control dentro de la órbita anatómica o el espacio morfológico. El modelo es el de un sistema dinámico, el flujo de coordenadas y el control del campo vectorial relacionado a través de La vista hamiltoniana reparametriza la distribución del momento en términos del momento conjugado o momento canónico , introducido como un multiplicador de Lagrange que restringe la velocidad lagrangiana . : ${\ Displaystyle t \ mapsto \ phi _ {t} \ in \ operatorname {Diff} _ {V}}$${\ Displaystyle t \ mapsto v_ {t} \ in V}$${\ displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ cdot \ phi _ {t}, \ phi _ {0} = id.}$${\ Displaystyle Av \ en V ^ {*}}$ ${\ Displaystyle p: {\ dot {\ phi}} \ mapsto (p \ mid {\ dot {\ phi}})}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}, v_ {t}) = \ int _ {X} p_ {t} \ cdot (v_ {t} \ circ \ phi _ {t}) dx - {\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} dx.}$

Esta función es el hamiltoniano extendido. El principio máximo de Pontryagin proporciona el campo vectorial de optimización que determina el flujo geodésico satisfactorio , así como el hamiltoniano reducido. ${\ displaystyle {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}, \ phi _ {0} = id,}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}) \ doteq \ max _ {v} H (\ phi _ {t}, p_ {t}, v) \.}$

El multiplicador de Lagrange en su acción como forma lineal tiene su propio producto interno del momento canónico que actúa sobre la velocidad del flujo que depende de la forma, por ejemplo, para los puntos de referencia una suma, para las superficies una integral de superficie, y. para los volúmenes es una integral de volumen con respecto a on . En todos los casos, los granos verdes tienen pesos que son el momento canónico que evoluciona de acuerdo con una ecuación diferencial ordinaria que corresponde a EL, pero es la reparametrización geodésica en el momento canónico. El campo vectorial de optimización viene dado por ${\ displaystyle dx}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$

${\ Displaystyle v_ {t} \ doteq \ arg max_ {v} H (\ phi _ {t}, p_ {t}, v)}$

con la dinámica del momento canónico reparametrizar el campo vectorial a lo largo de la geodésica

${\ Displaystyle {\ begin {cases} {\ dot {\ phi}} _ {t} = {\ frac {\ parcial H (\ phi _ {t}, p_ {t})} {\ parcial p}} \ \ {\ dot {p}} _ {t} = - {\ frac {\ parcial H (\ phi _ {t}, p_ {t})} {\ parcial \ phi}} \\\ end {cases}} }$

( Dinámica hamiltoniana )

Estacionariedad de la energía cinética y hamiltoniana a lo largo de Euler-Lagrange

Mientras que los campos vectoriales se extienden por todo el espacio de fondo de , los flujos geodésicos asociados a las subvariedades tienen un momento de forma euleriana que evoluciona como una función generalizada concentrada en las subvariedades. Para los puntos de referencia, las geodésicas tienen un momento de forma euleriana que es una superposición de distribuciones delta que viajan con el número finito de partículas; el flujo difeomórfico de coordenadas tiene velocidades en el rango de los granos de Green ponderados. Para las superficies, la cantidad de movimiento es una integral de la superficie de las distribuciones delta que viajan con la superficie. ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle Av_ {t} \ in V ^ {*}}$

Las geodésicas que conectan los sistemas de coordenadas que satisfacen EL-General tienen una estacionariedad del Lagrangiano. El hamiltoniano está dado por el extremo a lo largo de la trayectoria , igual a la energía cinética de Lagrange y es estacionario a lo largo de EL-General . Definiendo la velocidad geodésica en la identidad , luego a lo largo de la geodésica ${\ Displaystyle t \ in [0,1]}$${\ Displaystyle H (\ phi, p) = \ max _ {v} H (\ phi, p, v)}$${\ Displaystyle v_ {0} = \ arg \ max _ {v} H (\ phi _ {0}, p_ {0}, v)}$

${\ Displaystyle H (\ phi _ {t}, p_ {t}) = H (\ phi _ {0}, p_ {0}) = {\ frac {1} {2}} \ int _ {X} p_ {0} \ cdot v_ {0} dx = {\ frac {1} {2}} \ int _ {X} Av_ {0} \ cdot v_ {0} dx = {\ frac {1} {2}} \ int _ {X} Av_ {t} \ cdot v_ {t} dx}$

( Hamiltoniano-geodésicas )

La estacionariedad del hamiltoniano demuestra la interpretación del multiplicador de Lagrange como impulso; integrado contra la velocidad da densidad de energía. El impulso canónico tiene muchos nombres. En control óptimo , los flujos se interpretan como el estado y se interpretan como estado conjugado o momento conjugado. La geodesia de EL implica la especificación de los campos vectoriales o el momento euleriano en , o la especificación del momento canónico determina el flujo. ${\ Displaystyle {\ dot {\ phi}}}$${\ Displaystyle \ phi}$${\ Displaystyle p}$${\ Displaystyle v_ {0}}$${\ Displaystyle Av_ {0}}$${\ Displaystyle t = 0}$${\ Displaystyle p_ {0}}$

La métrica de los flujos geodésicos de puntos de referencia, superficies y volúmenes dentro de la órbita.

En anatomía computacional, las subvariedades son conjuntos de puntos, curvas, superficies y subvolúmenes que son las primitivas básicas. Los flujos geodésicos entre las subvariedades determinan la distancia y forman las herramientas básicas de medición y transporte de la difeomorfometría . En la geodésica tiene un campo vectorial determinado por el momento conjugado y el núcleo de Green del operador inercial que define el momento euleriano . La distancia métrica entre los sistemas de coordenadas conectados a través de la geodésica determinada por la distancia inducida entre la identidad y el elemento del grupo: ${\ Displaystyle t = 0}$${\ Displaystyle v_ {0} = Kp_ {0}}$${\ Displaystyle K = A ^ {- 1}}$

${\ Displaystyle d_ {Diff_ {V}} (id, \ varphi) = \ | Log_ {id} (\ varphi) \ | _ {V} = \ | v_ {0} \ | _ {V} = {\ sqrt {2H (id, p_ {0})}}}$

Leyes de conservación sobre el impulso de la forma difeomórfica para la anatomía computacional

Dada la mínima acción, existe una definición natural de impulso asociada a coordenadas generalizadas; la cantidad que actúa contra la velocidad da energía. El campo ha estudiado dos formas, el momento asociado al campo vectorial euleriano denominado momento de forma difeomórfica euleriana , y el momento asociado a las coordenadas iniciales o coordenadas canónicas denominado momento de forma difeomórfica canónica . Cada uno tiene una ley de conservación. La conservación del impulso va de la mano con EL-General . En anatomía computacional, es el Momento Euleriano ya que cuando se integra contra la velocidad Euleriana da densidad de energía; operador el momento de inercia generalizado u operador de inercia que, actuando sobre la velocidad euleriana, da un momento que se conserva a lo largo de la geodésica:${\ displaystyle Av}$${\ Displaystyle v}$${\ Displaystyle A}$

${\ Displaystyle {\ begin {matrix} {\ text {Euleriano}} & \ \ \ \ {\ frac {d} {dt}} \ int _ {X} Av_ {t} \ cdot ((D \ phi _ { t}) w) \ circ \ phi _ {t} ^ {- 1}) dx = 0 \, \ t \ in [0,1]. \\ & \\ {\ text {Canonical}} & \ \ \ \ \ \ \ \ \ \ \ {\ frac {d} {dt}} \ int _ {X} p_ {t} \ cdot ((D \ phi _ {t}) w) dx = 0 \, \ t \ en [0,1] \ {\ text {para todos}} \ w \ in V \. \ end {matriz}}}$

( Euler-Conservación-Energía-constante )

La conservación del impulso de la forma euleriana se muestra y sigue de EL-General ; La conservación del impulso canónico se mostró en

Interpolación geodésica de información entre sistemas de coordenadas mediante problemas variacionales

La construcción de correspondencias difeomórficas entre formas calcula las coordenadas del campo vectorial inicial y los pesos asociados en los granos verdes . Estas coordenadas iniciales se determinan mediante la coincidencia de formas, lo que se denomina Mapeo métrico difeomórfico de deformación grande (LDDMM) . LDDMM se ha resuelto para puntos de referencia con y sin correspondencia y para coincidencias de imágenes densas. curvas, superficies, imágenes densas de vectores y tensores, y varifolds eliminando la orientación. LDDMM calcula los flujos geodésicos del EL-General en las coordenadas del objetivo, agregando a la integral de acción una condición de coincidencia de punto final que mide la correspondencia de los elementos en la órbita bajo la transformación del sistema de coordenadas. Se examinó la existencia de soluciones para la concordancia de imágenes. La solución del problema variacional satisface el EL-General para con condición de frontera. ${\ Displaystyle v_ {0} \ in V}$${\ Displaystyle p_ {0}}$${\ Displaystyle {\ frac {1} {2}} \ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt}$${\ Displaystyle E: \ phi _ {1} \ rightarrow R ^ {+}}$${\ Displaystyle t \ in [0,1)}$

Emparejamiento basado en minimizar la acción de la energía cinética con la condición del punto final

${\ Displaystyle {\ text {min}} _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}, \ phi _ {0} = id} C (\ phi) \ doteq {\ frac {1} {2}} \ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt + E (\ phi _ {1})}$

${\ Displaystyle {\ begin {cases} {\ text {Euler Conservation}} \ \ \ \ \ \ \ \ \ & \ \ \ {\ frac {d} {dt}} Av_ {t} + ad_ {v_ {t} } ^ {*} (Av_ {t}) = 0, \ t \ in [0,1) \, \\ {\ text {Condición de límite}} & \ \ \ \ phi _ {0} = id, Av_ { 1} = - {\ frac {\ E parcial (\ phi)} {\ parcial \ phi}} | _ {\ phi = \ phi _ {1}} \. \ End {casos}}}$

La conservación de EL-General extiende el BC al resto del camino . El problema de coincidencia inexacta con el término de coincidencia de punto final tiene varias formas alternativas. Una de las ideas clave de la estacionariedad del hamiltoniano a lo largo de la solución geodésica es que el costo de funcionamiento integrado se reduce al costo inicial en t = 0, las geodésicas del EL-General están determinadas por su condición inicial . ${\ Displaystyle t = 1}$${\ Displaystyle t \ in [0,1)}$${\ Displaystyle E (\ phi _ {1})}$${\ Displaystyle v_ {0}}$

El coste de funcionamiento se reduce al coste inicial determinado por de Kernel-Surf.-Land.-Geodesics . ${\ Displaystyle v_ {0} = Kp_ {0}}$

Emparejamiento basado en disparos geodésicos

${\ Displaystyle \ min _ {v_ {0}} C (v_ {0}) \ doteq {\ frac {1} {2}} \ int _ {X} Av_ {0} \ cdot v_ {0} dx + E (\ mathrm {Exp} _ {\ mathrm {id}} (v_ {0}) \ cdot I_ {0}) \;}$

${\ Displaystyle \ min _ {p_ {0}} C (p_ {0}) = {\ frac {1} {2}} \ int _ {X} p_ {0} \ cdot Kp_ {0} dx + E ( \ mathrm {Exp} _ {\ text {id}} (Kp_ {0}) \ cdot I_ {0})}$

El problema de emparejamiento explícitamente indexado a la condición inicial se denomina disparo, que también puede reparamerizarse mediante el impulso conjugado . ${\ Displaystyle v_ {0}}$${\ Displaystyle p_ {0}}$

Coincidencia de imágenes densas en anatomía computacional

La coincidencia de imágenes densas tiene una larga historia ahora con los primeros esfuerzos que explotan un marco de deformación pequeña. Las grandes deformaciones comenzaron a principios de la década de 1990, con la primera existencia de soluciones al problema variacional de los flujos de difeomorfismos para el emparejamiento de imágenes densas establecido en. Beg se resolvió mediante uno de los primeros algoritmos LDDMM basado en resolver el emparejamiento variacional con el punto final definido por el denso. imágenes con respecto a los campos vectoriales, tomando variaciones con respecto a los campos vectoriales. Otra solución para el emparejamiento de imágenes densas reparametriza el problema de optimización en términos del estado que da la solución en términos de la acción infinitesimal definida por la ecuación de advección . ${\ Displaystyle q_ {t} \ doteq I \ circ \ phi _ {t} ^ {- 1}, q_ {0} = I}$

Coincidencia de imágenes densas LDDMM

Para LDDMM de Beg, denote la imagen con acción de grupo . Viendo esto como un problema de control óptimo, el estado del sistema es el flujo difeomórfico de coordenadas , con la dinámica que relaciona el control con el estado dada por . La condición de coincidencia del punto final da el problema variacional ${\ Displaystyle I (x), x \ en X}$${\ Displaystyle \ phi \ cdot I \ doteq I \ circ \ phi ^ {- 1}}$${\ Displaystyle \ phi _ {t}, t \ en [0,1]}$${\ Displaystyle v_ {t}, t \ in [0,1]}$${\ Displaystyle {\ dot {\ phi}} = v \ circ \ phi}$${\ Displaystyle E (\ phi _ {1}) \ doteq \ | I \ circ \ phi _ {1} ^ {- 1} -I ^ {\ prime} \ | ^ {2}}$

${\ Displaystyle {\ begin {matrix} & \ \ \ \ \ \ min _ {v: {\ dot {\ phi}} = v \ circ \ phi} C (v) \ doteq {\ frac {1} {2 }} \ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt + {\ frac {1} {2}} \ int _ {{\ mathbb {R}} ^ {3}} | I \ circ \ phi _ {1} ^ {- 1} (x) -I ^ {\ prime} (x) | ^ {2} dx \ end {matriz}}}$

( Coincidencia de imágenes densas )

${\ displaystyle {\ begin {cases} & {\ text {Condición del punto final:}} \ \ \ \ \ \ Av_ {1} = \ mu _ {1} dx, \ mu _ {1} = (I \ circ \ phi _ {1} ^ {- 1} -I ^ {\ prime}) \ nabla (I \ circ \ phi _ {1} ^ {- 1}) \, \\ & {\ text {Conservación:}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {t} = \ mu _ {t} \, dx, \ \ mu _ {t} = (D \ phi _ {t} ^ {- 1} ) ^ {T} \ mu _ {0} \ circ \ phi _ {t} ^ {- 1} | D \ phi _ {t} ^ {- 1} | \. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ mu _ {0} = (II ^ {\ prime} \ circ \ phi _ {1}) \ nabla I | D \ phi _ {1} | \. \\\ end {cases}}}$

El algoritmo LDDMM iterativo de Beg tiene puntos fijos que satisfacen las condiciones necesarias del optimizador. El algoritmo iterativo se proporciona en el algoritmo LDDMM de Beg para la comparación de imágenes densas .

LDDMM hamiltoniano en estado advectado reducido

Denote la Imagen , con el estado y el estado relacionado con la dinámica y el control dado por el término advectivo . El punto final da el problema variacional ${\ Displaystyle I (x), x \ en X}$${\ Displaystyle q_ {t} \ doteq I \ circ \ phi _ {t} ^ {- 1}}$ ${\ Displaystyle {\ dot {q}} _ {t} = - \ nabla q_ {t} \ cdot v_ {t}}$${\ Displaystyle E (q_ {1}) \ doteq \ | q_ {1} -I ^ {\ prime} \ | ^ {2}}$

${\ Displaystyle {\ begin {matrix} & \ \ \ \ \ \ min _ {q: {\ dot {q}} = v \ circ q} C (v) \ doteq {\ frac {1} {2}} \ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dxdt + {\ frac {1} {2}} \ int _ {{\ mathbb {R}} ^ { 3}} | q_ {1} (x) -I ^ {\ prime} (x) | ^ {2} dx \ end {matriz}}}$

( Coincidencia de imágenes densas )

El LDDMM hamiltoniano iterativo de Viallard tiene puntos fijos que satisfacen las condiciones necesarias del optimizador.

Coincidencia de imágenes del tensor de difusión en anatomía computacional

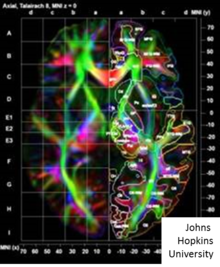
El emparejamiento del tensor LDDMM denso toma las imágenes como vectores 3x1 y tensores 3x3 para resolver el problema de emparejamiento variacional entre el sistema de coordenadas basado en los principales vectores propios de la imagen de resonancia magnética del tensor de difusión (DTI) que consta del -tensor en cada vóxel. Varias de las acciones grupales definidas en base a la norma de matrices de Frobenius entre matrices cuadradas . En la figura adjunta se muestra una imagen DTI ilustrada mediante su mapa de colores que representa las orientaciones de los vectores propios de la matriz DTI en cada vóxel con el color determinado por la orientación de las direcciones. Denotar la imagen de tensor con elementos Eigen , . ${\ Displaystyle M (x), x \ in {\ mathbb {R}} ^ {3}}$${\ Displaystyle 3 \ times 3}$${\ Displaystyle \ | A \ | _ {F} ^ {2} \ doteq traceA ^ {T} A}$${\ Displaystyle 3 \ times 3}$${\ Displaystyle M (x), x \ in {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ {\ lambda _ {i} (x), e_ {i} (x), i = 1,2,3 \}}$${\ Displaystyle \ lambda _ {1} \ geq \ lambda _ {2} \ geq \ lambda _ {3}}$

La transformación del sistema de coordenadas basada en imágenes DTI ha aprovechado dos acciones, una basada en el principio de vector propio o matriz completa .

El emparejamiento LDDMM basado en el vector propio principal de la matriz del tensor de difusión toma la imagen como un campo de vector unitario definido por el primer vector propio. La acción grupal se convierte ${\ Displaystyle I (x), x \ in {\ mathbb {R}} ^ {3}}$

${\ Displaystyle \ varphi \ cdot I = {\ begin {cases} {\ frac {D _ {\ varphi ^ {- 1}} \ varphi I \ circ \ varphi ^ {- 1} \ | I \ circ \ varphi ^ { -1} \ |} {\ | D _ {\ varphi ^ {- 1}} \ varphi I \ circ \ varphi ^ {- 1} \ |}} & I \ circ \ varphi \ neq 0; \\ 0 & {\ text {de lo contrario.}} \ end {cases}}}$

La coincidencia de LDDMM basada en toda la matriz tensorial tiene la acción de grupo se convierte en vectores propios transformados ${\ Displaystyle \ varphi \ cdot M = (\ lambda _ {1} {\ hat {e}} _ {1} {\ hat {e}} _ {1} ^ {T} + \ lambda _ {2} { \ hat {e}} _ {2} {\ hat {e}} _ {2} ^ {T} + \ lambda _ {3} {\ hat {e}} _ {3} {\ hat {e}} _ {3} ^ {T}) \ circ \ varphi ^ {- 1},}$

${\ Displaystyle {\ begin {alineado} {\ hat {e}} _ {1} & = {\ frac {D \ varphi e_ {1}} {\ | D \ varphi e_ {1} \ |}} \, \ \ \ {\ hat {e}} _ {2} = {\ frac {D \ varphi e_ {2} - \ langle {\ hat {e}} _ {1}, D \ varphi e_ {2} \ rangle {\ hat {e}} _ {1}} {\ sqrt {\ | D \ varphi e_ {2} \ | ^ {2} - \ langle {\ hat {e}} _ {1}, D \ varphi e_ {2} \ rangle ^ {2}}}} \, \ \ \ {\ hat {e}} _ {3} = {\ hat {e}} _ {1} \ times {\ hat {e}} _ {2} \ end {alineado}}}$.

El problema variacional que coincide con el vector propio principal o la matriz se describe LDDMM Tensor Image Matching .

Coincidencia de imágenes de difusión de alta resolución angular (HARDI) en anatomía computacional

La imagen por difusión de alta resolución angular (HARDI) aborda la conocida limitación de DTI, es decir, DTI solo puede revelar una orientación de fibra dominante en cada ubicación. HARDI mide la difusión a lo largo de direcciones distribuidas uniformemente en la esfera y puede caracterizar geometrías de fibra más complejas. HARDI se puede utilizar para reconstruir una función de distribución de orientación (ODF) que caracteriza el perfil angular de la función de densidad de probabilidad de difusión de las moléculas de agua. La ODF es una función definida en una esfera unidad, . ${\ Displaystyle n}$${\ Displaystyle {\ mathbb {S}} ^ {2}}$

El emparejamiento denso LDDMM ODF toma los datos HARDI como ODF en cada vóxel y resuelve el problema de variacional LDDMM en el espacio de ODF. En el campo de la geometría de la información , el espacio de ODF forma una variedad de Riemann con la métrica de Fisher-Rao. A los efectos del mapeo LDDMM ODF, se elige la representación de raíz cuadrada porque es una de las representaciones más eficientes encontradas hasta la fecha, ya que las diversas operaciones de Riemann, como geodésicas, mapas exponenciales y mapas de logaritmos, están disponibles en forma cerrada. A continuación, denote ODF de raíz cuadrada ( ) como , donde no es negativo para garantizar la unicidad y . El problema variacional para el emparejamiento supone que se pueden generar dos volúmenes ODF de uno a otro a través de flujos de difeomorfismos , que son soluciones de ecuaciones diferenciales ordinarias a partir del mapa de identidad . Denotan la acción del difeomorfismo en plantilla como , , son, respectivamente, las coordenadas de la esfera unidad, y el dominio de la imagen, con el objetivo indexadas de manera similar, , , . ${\ Displaystyle {\ sqrt {\ text {ODF}}}}$${\ Displaystyle \ psi ({\ bf {s}})}$${\ Displaystyle \ psi ({\ bf {s}})}$${\ Displaystyle \ int _ {{\ bf {s}} \ in {\ mathbb {S}} ^ {2}} \ psi ^ {2} ({\ bf {s}}) d {\ bf {s} } = 1}$${\ Displaystyle \ phi _ {t}}$${\ Displaystyle {\ dot {\ phi}} _ {t} = v_ {t} (\ phi _ {t}), t \ in [0,1],}$${\ Displaystyle \ phi _ {0} = {id}}$${\ Displaystyle \ phi _ {1} \ cdot \ psi _ {\ mathrm {temp}} ({\ bf {s}}, x)}$${\ Displaystyle {\ bf {s}} \ in {{\ mathbb {S}} ^ {2}}}$${\ Displaystyle x \ in X}$${\ Displaystyle {{\ mathbb {S}} ^ {2}}}$${\ Displaystyle \ psi _ {\ mathrm {targ}} ({\ bf {s}}, x)}$${\ Displaystyle {\ bf {s}} \ in {{\ mathbb {S}} ^ {2}}}$${\ Displaystyle x \ in X}$

La acción de grupo del difeomorfismo en la plantilla se da de acuerdo con

${\ Displaystyle \ phi _ {1} \ cdot \ psi (x) \ doteq (D \ phi _ {1}) \ psi \ circ \ phi _ {1} ^ {- 1} (x), x \ en X }$,

donde es el jacobiano de la ODF transformada afín y se define como ${\ Displaystyle (D \ phi _ {1})}$${\ Displaystyle {\ begin {alineado} (D \ phi _ {1}) \ psi \ circ \ phi _ {1} ^ {- 1} (x) = {\ sqrt {\ frac {\ det {{\ bigl (} D _ {\ phi _ {1} ^ {- 1}} \ phi _ {1} {\ bigr)} ^ {- 1}}} {\ left \ | {{\ bigl (} D _ {\ phi _ {1} ^ {- 1}} \ phi _ {1} {\ bigr)} ^ {- 1}} {\ bf {s}} \ right \ | ^ {3}}}} \ quad \ psi \ left ({\ frac {(D _ {\ phi _ {1} ^ {- 1}} \ phi _ {1} {\ bigr)} ^ {- 1} {\ bf {s}}} {\ | (D_ { \ phi _ {1} ^ {- 1}} \ phi _ {1} {\ bigr)} ^ {- 1} {\ bf {s}} \ |}}, \ phi _ {1} ^ {- 1 } (x) \ derecha). \ end {alineado}}}$

Esta acción de grupo de difeomorfismos en ODF reorienta el ODF y refleja cambios tanto en la magnitud como en las direcciones de muestreo de debido a la transformación afín. Garantiza que la fracción de volumen de las fibras orientadas hacia un parche pequeño debe permanecer igual después de que el parche se haya transformado. ${\ Displaystyle \ psi}$${\ Displaystyle {\ bf {s}}}$

El problema variacional LDDMM se define como

${\ Displaystyle {\ begin {alineado} C (v) = \ inf _ {v: {\ dot {\ phi}} _ {t} = v_ {t} \ circ \ phi _ {t}, \ phi _ { 0} = {id}} \ int _ {0} ^ {1} \ int _ {X} Av_ {t} \ cdot v_ {t} dx \ dt + \ lambda \ int _ {x \ in \ Omega} \ | \ log _ {(D \ phi _ {1}) \ psi _ {\ mathrm {temp}} \ circ \ phi _ {1} ^ {- 1} (x)} (\ psi _ {\ mathrm {targ} } (x)) \ | _ {(D \ phi _ {1}) \ psi _ {\ mathrm {temp}} \ circ \ phi _ {1} ^ {- 1} (x)} ^ {2} dx \ end {alineado}}}$.

donde el logaritmo de se define como ${\ Displaystyle \ psi _ {1}, \ psi _ {2} \ in \ Psi}$

${\ Displaystyle {\ begin {alineado} \ | \ log _ {\ psi _ {1}} (\ psi _ {2}) \ | _ {\ psi _ {1}} = \ cos ^ {- 1} \ langle \ psi _ {1}, \ psi _ {2} \ rangle = \ cos ^ {- 1} \ left (\ int _ {{\ bf {s}} \ in {\ mathbb {S}} ^ {2 }} \ psi _ {1} ({\ bf {s}}) \ psi _ {2} ({\ bf {s}}) d {\ bf {s}} \ right), \ end {alineado}} }$

donde es el producto escalar normal entre los puntos de la esfera debajo de la métrica. ${\ Displaystyle \ langle \ cdot, \ cdot \ rangle}$${\ Displaystyle \ mathrm {L} ^ {2}}$

Este algoritmo de mapeo LDDMM-ODF se ha utilizado ampliamente para estudiar la degeneración de la materia blanca del cerebro en el envejecimiento, la enfermedad de Alzheimer y la demencia vascular. El atlas de materia blanca del cerebro generado en base a ODF se construye mediante estimación bayesiana. El análisis de regresión en ODF se desarrolla en el espacio del colector ODF en.

Metamorfosis

El principal modo de variación representado por el modelo de órbita es el cambio de coordenadas. Para entornos en los que los pares de imágenes no están relacionados por difeomorfismos pero tienen variación fotométrica o variación de imagen no representada por la plantilla, se introdujo el modelado de apariencia activa , originalmente por Edwards-Cootes-Taylor y en imágenes médicas 3D en. En el contexto de La anatomía computacional en la que se han estudiado las métricas de la órbita anatómica, se introdujo la metamorfosis para modelar estructuras como tumores y los cambios fotométricos que no residen en la plantilla para los modelos de imagen de resonancia magnética, con muchos desarrollos posteriores que extienden el marco de la metamorfosis.

Para que la imagen coincida con la imagen, el marco de metamorfosis amplía la acción de modo que con la acción . En este escenario, la metamorfosis combina la transformación del sistema de coordenadas difeomórficas de la anatomía computacional, así como las primeras tecnologías de transformación que solo desvanecían o modificaban la intensidad fotométrica o de la imagen solo. ${\ Displaystyle t \ mapsto (\ phi _ {t}, I_ {t})}$${\ Displaystyle \ phi _ {t} \ cdot I_ {t} \ doteq I_ {t} \ circ \ phi _ {t} ^ {- 1}}$

Entonces, el problema de emparejamiento toma una forma con condiciones de frontera de igualdad:

${\ Displaystyle \ min _ {(v, I)} {\ frac {1} {2}} \ int _ {0} ^ {1} \ left (\ int _ {X} Av_ {t} \ cdot v_ { t} dx + \ | {\ dot {I}} _ {t} \ circ \ phi _ {t} ^ {- 1} \ | ^ {2} / \ sigma ^ {2} \ right) \, dt {\ texto {sujeto a}} \ \ phi _ {0} = id, I_ {0} = {\ text {fijo}}, I_ {1} = {\ text {fijo}}}$

Coincidencia de puntos de referencia, curvas, superficies

La transformación de sistemas de coordenadas basados ​​en puntos de referencia o características de marcadores fiduciales se remonta a los primeros trabajos de Bookstein sobre métodos de splines de deformación pequeña para interpolar correspondencias definidas por puntos fiduciales con el espacio de fondo bidimensional o tridimensional en el que se definen los fiduciales. Los métodos de hitos de gran deformación aparecieron a fines de la década de 1990. La figura anterior muestra una serie de puntos de referencia asociados a tres estructuras cerebrales, la amígdala, la corteza entorrinal y el hipocampo.

Hacer coincidir objetos geométricos como distribuciones de puntos, curvas o superficies sin etiquetar es otro problema común en la anatomía computacional. Incluso en el entorno discreto en el que estos se dan comúnmente como vértices con mallas, no hay correspondencias predeterminadas entre puntos a diferencia de la situación de puntos de referencia descrita anteriormente. Desde el punto de vista teórico, mientras que cualquier subvariedad en , puede ser parametrizado en cartas locales , todos reparametrizations de estos gráficos dan geométricamente el mismo colector. Por lo tanto, al principio de la anatomía computacional, los investigadores han identificado la necesidad de representaciones invariantes de parametrización. Un requisito indispensable es que el término de coincidencia de punto final entre dos subvariedades sea en sí mismo independiente de sus parametrizaciones. Esto se puede lograr a través de conceptos y métodos tomados de la teoría de medidas geométricas , en particular corrientes y pliegues variables que se han utilizado ampliamente para la coincidencia de curvas y superficies. ${\ Displaystyle X}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle d = 1,2,3}$${\ displaystyle m: u \ in U \ subset {\ mathbb {R}} ^ {0,1,2,3} \ rightarrow {\ mathbb {R}} ^ {3}}$

Punto de referencia o coincidencia de puntos con correspondencia

Denominada la forma marcada con un punto final , el problema variacional se convierte en ${\ Displaystyle X \ doteq \ {x_ {1}, \ dots, x_ {n} \} \ subset {\ mathbb {R}} ^ {3}}$${\ Displaystyle E (\ phi _ {1}) \ doteq \ textstyle \ sum _ {i} \ Displaystyle \ | \ phi _ {1} (x_ {i}) - x_ {i} ^ {\ prime} \ | ^ {2}}$

.${\ Displaystyle {\ begin {matrix} & \ \ \ \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int (Av_ {t} | v_ {t}) dt + {\ frac {1} {2}} \ sum _ {i} \ | \ phi _ {1} (x_ {i} ) -x_ {i} ^ {\ prime} \ | ^ {2} \ end {matriz}}}$

( Coincidencia de puntos de referencia )

El impulso euleriano geodésico es una función generalizada , apoyada en el conjunto de hitos en el problema variacional. La condición de punto final con conservación implica el impulso inicial en la identidad del grupo: ${\ Displaystyle \ Displaystyle Av_ {t} \ in V ^ {*} \ textstyle, t \ in [0,1]}$

${\ Displaystyle {\ begin {cases} & {\ text {Condición del punto final:}} \ \ \ \ \ Av_ {1} = \ sum _ {i = 1} ^ {n} p_ {1} (i) \ delta _ {\ phi _ {1} (x_ {i})}, p_ {1} (i) = (x_ {i} ^ {\ prime} - \ phi _ {1} (x_ {i})) \, \\ & {\ text {Conservación:}} \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {t} = \ sum _ {i = 1} ^ {n} p_ {t} (i) \ delta _ {\ phi _ {t} (x_ {i})}, \ p_ {t} (i) = (D \ phi _ {t1}) _ {| \ phi _ {t} (x_ {i}) } ^ {T} p_ {1} (i) \, \ \ phi _ {t1} \ doteq \ phi _ {1} \ circ \ phi _ {t} ^ {- 1} \, \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Av_ {0} = \ sum _ {i} \ delta _ {x_ {i}} (\ cdot) p_ {0} (i) \ {\ text {con}} \ \ p_ {0} (i) = (D \ phi _ {1}) _ {| x_ {i}} ^ {T} (x_ {i} ^ {\ prime} - \ phi _ {1} (x_ {i})) \ end {cases}}}$

Se proporciona el algoritmo iterativo para el mapeo métrico difeomórfico de grandes deformaciones para puntos de referencia .

Coincidencia de medidas: puntos de referencia no registrados

Glaunes y sus colaboradores introdujeron por primera vez la coincidencia difeomórfica de conjuntos de puntos en el entorno general de distribuciones coincidentes. A diferencia de los puntos de referencia, esto incluye en particular la situación de nubes de puntos ponderadas sin correspondencias predefinidas y posiblemente diferentes cardinalidades. La plantilla y las nubes de puntos discretas objetivo se representan como dos sumas ponderadas de Diracs y viven en el espacio de medidas firmadas de . El espacio está equipado con una métrica de Hilbert obtenida de un kernel positivo real en adelante , dando la siguiente norma: ${\ Displaystyle \ mu _ {m} = \ sum _ {i = 1} ^ {n} \ rho _ {i} \ delta _ {x_ {i}}}$${\ Displaystyle \ mu _ {m ^ {\ prime}} = \ sum _ {i = 1} ^ {n ^ {\ prime}} \ rho _ {i} ^ {\ prime} \ delta _ {x_ {i } ^ {\ prime}}}$${\ Displaystyle \ mathbb {R} ^ {3}}$${\ Displaystyle k (x, y)}$${\ Displaystyle \ mathbb {R} ^ {3}}$

${\ Displaystyle \ | \ mu _ {m} \ | _ {\ mathrm {mea}} ^ {2} = \ sum _ {i, j = 1} ^ {n} \ rho _ {i} \ rho _ { j} k (x_ {i}, x_ {j})}$

El problema de coincidencia entre una plantilla y la nube de puntos de destino se puede formular utilizando esta métrica del kernel para el término de coincidencia de punto final:

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt + {\ frac {1} {2}} \ | \ mu _ {\ phi _ {1} \ cdot m} - \ mu _ {m ^ {\ prime }} \ | _ {\ mathrm {mea}} ^ {2}}$

donde es la distribución transportada por la deformación. ${\ Displaystyle \ mu _ {\ phi _ {1} \ cdot m} = \ sum _ {i = 1} ^ {n} \ rho _ {i} \ delta _ {\ phi _ {1} (x_ {i })}}$

Coincidencia de curvas

En el caso unidimensional, una curva en 3D se puede representar mediante una incrustación , y la acción de grupo de Diff se convierte en . Sin embargo, la correspondencia entre curvas e incrustaciones no es una a una, ya que cualquier reparametrización , ya que un difeomorfismo del intervalo [0,1], representa geométricamente la misma curva. Para preservar esta invariancia en el término de coincidencia de punto final, se pueden considerar varias extensiones del enfoque anterior de coincidencia de medidas de dimensión 0. ${\ displaystyle m: u \ in [0,1] \ rightarrow {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ phi \ cdot m = \ phi \ circ m}$${\ Displaystyle m \ circ \ gamma}$${\ Displaystyle \ gamma}$

• Coincidencia de curvas con corrientes

En la situación de curvas orientadas, las corrientes proporcionan un entorno eficiente para construir términos de coincidencia invariantes. En tal representación, las curvas se interpretan como elementos de un espacio funcional dual a los campos del vector espacial, y se comparan a través de las normas del núcleo en estos espacios. Emparejamiento de dos curvas y escribe eventualmente como el problema variacional ${\ Displaystyle m}$${\ Displaystyle m ^ {\ prime}}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt + {\ frac {1} {2}} \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m} - {\ mathcal { C}} _ ​​{m ^ {\ prime}} \ | _ {\ mathrm {cur}} ^ {2}}$

con el término de punto final se obtiene de la norma ${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m} - {\ mathcal {C}} _ ​​{m ^ {\ prime} } \ | _ {\ mathrm {cur}} ^ {2} / 2}$

${\ Displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}} ^ {2} = \ int _ {0} ^ {1} \ int _ {0} ^ {1 } K_ {C} (metro (u), metro (v)) \ parcial m (u) \ cdot \ parcial m (v) \, du \, dv}$

siendo la derivada el vector tangente a la curva y un núcleo de matriz dado de . Tales expresiones son invariantes a cualquier reparametrización positiva de y , y por lo tanto todavía dependen de la orientación de las dos curvas. ${\ Displaystyle \ parcial m (u)}$${\ Displaystyle K _ {\ mathcal {C}}}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle m}$${\ Displaystyle m '}$

• Coincidencia de curvas con varifolds

Varifold es una alternativa a las corrientes cuando la orientación se convierte en un problema, como por ejemplo en situaciones que involucran múltiples haces de curvas para las cuales no se puede definir una orientación "consistente". Varifolds extienden directamente las medidas de dimensión 0 al agregar una dirección espacial tangente adicional a la posición de los puntos, lo que lleva a representar curvas como medidas sobre el producto de y el Grassmanniano de todas las líneas rectas en . El problema de concordancia entre dos curvas consiste en reemplazar el término de concordancia de punto final por con normas variables de la forma: ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {V}} _ {\ phi _ {1} \ cdot m} - {\ mathcal {V}} _ {m ^ {\ prime} } \ | _ {cur} ^ {2} / 2}$

${\ Displaystyle \ | {\ mathcal {V}} _ {m} \ | _ {var} ^ {2} = \ int _ {0} ^ {1} \ int _ {0} ^ {1} k _ {\ mathbb {R} ^ {3}} (m (u), m (v)) k _ {\ mathbf {Gr}} \ izquierda ([\ m parcial (u)], [\ m parcial (v)] \ derecha ) {|} \ m parcial (u) {|} {|} \ m parcial (v) {|} \, du \, dv}$

donde es la línea no orientada dirigida por el vector tangente y dos núcleos escalares respectivamente en y Grassmannian. Debido a la naturaleza no orientada inherente de la representación Grassmanniana, tales expresiones son invariantes a las reparametrizaciones positivas y negativas. ${\ Displaystyle [\ m parcial (u)]}$${\ Displaystyle \ parcial m (u)}$${\ Displaystyle k _ {\ mathbb {R} ^ {3}}, k _ {\ mathbf {Gr}}}$${\ Displaystyle \ mathbb {R} ^ {3}}$

Emparejamiento de superficie

La coincidencia de superficies comparte muchas similitudes con el caso de las curvas. Las superficies en se parametrizan en gráficos locales mediante incrustaciones , siendo todas las reparametrizaciones con un difeomorfismo de U equivalentes geométricamente. También se pueden utilizar corrientes y pliegues para formalizar el emparejamiento de superficies. ${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ displaystyle m: u \ in U \ subconjunto {\ mathbb {R}} ^ {2} \ rightarrow {\ mathbb {R}} ^ {3}}$${\ Displaystyle m \ circ \ gamma}$${\ Displaystyle \ gamma}$

• Emparejamiento de superficies con corrientes

Las superficies orientadas se pueden representar como 2 corrientes que son duales a 2 formas diferenciales. En , se pueden identificar más formas 2 con campos vectoriales a través del producto de cuña estándar de vectores 3D. En ese entorno, la coincidencia de superficies escribe nuevamente: ${\ Displaystyle {\ mathbb {R}} ^ {3}}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}} C (\ phi) \ doteq {\ frac {1} {2}} \ int ( Av_ {t} \ mid v_ {t}) \, dt + {\ frac {1} {2}} \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m} - {\ mathcal { C}} _ ​​{m ^ {\ prime}} \ | _ {\ mathrm {cur}} ^ {2}}$

con el término de punto final dado a través de la norma ${\ Displaystyle E (\ phi _ {1}) = \ | {\ mathcal {C}} _ ​​{\ phi _ {1} \ cdot m} - {\ mathcal {C}} _ ​​{m ^ {\ prime} } \ | _ {\ mathrm {cur}} ^ {2} / 2}$

${\ Displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}} ^ {2} = \ iint _ {U \ times U} K_ {C} (m (u), m (v)) {\ vec {n}} (u) \ cdot {\ vec {n}} (v) \, du \, dv}$

con el vector normal a la superficie parametrizado por . ${\ Displaystyle {\ vec {n}} = \ parcial _ {u_ {1}} m \ cuña \ parcial _ {u_ {2}} m}$${\ Displaystyle m}$

Este algoritmo de mapeo de superficies ha sido validado para superficies corticales del cerebro frente a CARET y FreeSurfer. El mapeo LDDMM para superficies multiescala se analiza en.

• Emparejamiento de superficies con varifolds

Para superficies no orientables o no orientadas, la estructura de múltiples pliegues suele ser más adecuada. Identificando la superficie paramétrica con un varifold en el espacio de medidas sobre el producto de y el Grassmanniano, uno simplemente reemplaza la métrica actual anterior por: ${\ Displaystyle m}$${\ Displaystyle {\ mathcal {V}} _ {m}}$${\ Displaystyle {\ mathbb {R}} ^ {3}}$${\ Displaystyle \ | {\ mathcal {C}} _ ​​{m} \ | _ {\ mathrm {cur}} ^ {2}}$

${\ Displaystyle \ | {\ mathcal {V}} _ {m} \ | _ {\ mathrm {var}} ^ {2} = \ iint _ {U \ times U} k _ {\ mathbb {R} ^ {3 }} (m (u), m (v)) k _ {\ mathbf {Gr}} \ left ([{\ vec {n}} (u)], [{\ vec {n}} (v)] \ derecha) {|} {\ vec {n}} (u) {|} {|} {\ vec {n}} (v) {|} \, du \, dv}$

donde es la línea (no orientada) dirigida por el vector normal a la superficie. ${\ Displaystyle [{\ vec {n}} (u)]}$

Crecimiento y atrofia de series de tiempo longitudinales

Hay muchos entornos en los que hay una serie de mediciones, una serie de tiempo con la que se emparejarán y fluirán los sistemas de coordenadas subyacentes. Esto ocurre, por ejemplo, en los modelos de crecimiento dinámico y atrofia y seguimiento de movimiento, como los que se han explorado en Se da una secuencia de tiempo observada y el objetivo es inferir el flujo de tiempo del cambio geométrico de coordenadas que llevan a los ejemplares o templarios a través del período de observaciones. .

El problema genérico de coincidencia de series de tiempo considera que la serie de tiempos es . El flujo se optimiza a la serie de costos dando problemas de optimización de la forma ${\ Displaystyle 0 <t_ {1} <\ dots t_ {K} = 1}$${\ Displaystyle E (t_ {k}), k = 1, \ dots, K}$

${\ Displaystyle \ min _ {\ phi: v = {\ dot {\ phi}} \ circ \ phi ^ {- 1}, \ phi _ {0} = id} C (\ phi) \ doteq {\ frac { 1} {2}} \ int _ {0} ^ {1} (Av_ {t} \ mid v_ {t}) \, dt + \ sum _ {k = 1} ^ {K} E (\ phi _ {t_ {k}})}$.

Hasta ahora se han ofrecido al menos tres soluciones, geodésica por partes, geodésica principal y splines.

El modelo de órbita aleatoria de anatomía computacional

El modelo de órbita aleatoria de anatomía computacional apareció por primera vez al modelar el cambio de coordenadas asociado a la aleatoriedad del grupo que actúa sobre las plantillas, lo que induce la aleatoriedad en la fuente de imágenes en la órbita anatómica de formas y formas y las observaciones resultantes a través de la técnica médica. Dispositivos de imagen. Un modelo de órbita aleatoria en el que la aleatoriedad en el grupo induce aleatoriedad en las imágenes fue examinado por el Grupo Euclidiano Especial para el reconocimiento de objetos en.

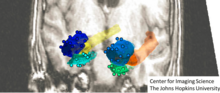
En la figura se muestra una representación de las órbitas aleatorias alrededor de cada ejemplar, generadas al aleatorizar el flujo al generar el campo de vector espacial tangente inicial en la identidad , y luego generar un objeto aleatorio . ${\ Displaystyle m_ {0} \ in {\ mathcal {M}}}$${\ Displaystyle v_ {0} \ in V}$${\ Displaystyle n \ doteq Exp_ {id} (v_ {0}) \ cdot m_ {0} \ in {\ mathcal {M}}}$

El modelo de órbita aleatoria induce lo anterior en formas e imágenes condicionadas en un atlas particular . Para ello el modelo generativo genera el campo medio como un cambio aleatorio de coordenadas de la plantilla según , donde el cambio difeomórfico de coordenadas se genera aleatoriamente a través de los flujos geodésicos. El prior en transformaciones aleatorias en es inducido por el flujo , con construido como un campo aleatorio gaussiano antes . La densidad de los observables aleatorios a la salida del sensor viene dada por ${\ Displaystyle I \ in {\ mathcal {I}}}$${\ Displaystyle I_ {a} \ in {\ mathcal {I}}}$${\ Displaystyle I}$${\ Displaystyle I \ doteq \ phi \ cdot I_ {a}}$${\ Displaystyle \ pi _ {Diff} (d \ phi)}$${\ Displaystyle Diff_ {V}}$${\ displaystyle Exp_ {id} (v)}$${\ Displaystyle v \ in V}$${\ Displaystyle \ pi _ {V} (dv)}$${\ Displaystyle I ^ {D} \ in {\ mathcal {I}} ^ {D}}$

${\ Displaystyle p (I ^ {D} | I_ {a}) = \ int _ {V} p (I ^ {D} | Exp_ {id} (v) \ cdot I_ {a}) \ pi _ {V } (dv) \.}$

En la Figura de la derecha se muestra la órbita de la caricatura, una pulverización aleatoria de las variedades subcorticales generadas al aleatorizar los campos vectoriales soportados sobre las subvariedades. ${\ Displaystyle v_ {0}}$

El modelo bayesiano de anatomía computacional

El modelo estadístico central de la anatomía computacional en el contexto de las imágenes médicas ha sido el modelo de canal de fuente de la teoría de Shannon ; la fuente es la plantilla deformable de imágenes , las salidas del canal son los sensores de imágenes con observables (ver Figura). ${\ Displaystyle I \ in {\ mathcal {I}}}$${\ Displaystyle I ^ {D} \ in {\ mathcal {I}} ^ {\ mathcal {D}}}$

Consulte El modelo bayesiano de anatomía computacional para las discusiones (i) Estimación de MAP con múltiples atlas, (ii) Segmentación de MAP con múltiples atlas, Estimación de MAP de plantillas de poblaciones.

Teoría de la forma estadística en anatomía computacional

La forma en anatomía computacional es una teoría local, que indexa formas y estructuras a plantillas a las que se asignan biyectivamente . La forma estadística en anatomía computacional es el estudio empírico de correspondencias difeomórficas entre poblaciones y sistemas de coordenadas de plantilla comunes. Esta es una fuerte desviación de los análisis de Procrustes y las teorías de la forma iniciadas por David G. Kendall en el sentido de que el grupo central de las teorías de Kendall son los grupos de Lie de dimensión finita, mientras que las teorías de la forma en la anatomía computacional se han centrado en el grupo de difeomorfismo, que para El primer orden a través del jacobiano se puede considerar como un campo, por lo tanto de dimensión infinita, de grupos de Lie de baja dimensión de escala y rotaciones.

El modelo de órbita aleatoria proporciona el escenario natural para comprender la forma empírica y las estadísticas de forma dentro de la anatomía computacional, ya que la no linealidad de la ley de probabilidad inducida en las formas y formas anatómicas se induce mediante la reducción a los campos vectoriales en el espacio tangente en la identidad de el grupo de difeomorfismo. El flujo sucesivo de la ecuación de Euler induce el espacio aleatorio de formas y formas . ${\ Displaystyle m \ in {\ mathcal {M}}}$${\ Displaystyle v_ {0} \ in V}$${\ Displaystyle Exp_ {id} (v_ {0}) \ cdot m \ in {\ mathcal {M}}}$

Realizar estadísticas empíricas en este espacio tangente en la identidad es la forma natural de inducir leyes de probabilidad en las estadísticas de forma. Dado que tanto los campos vectoriales como el momento euleriano están en un espacio de Hilbert, el modelo natural es uno de un campo aleatorio gaussiano, por lo que dada la función de prueba , los productos internos con las funciones de prueba tienen una distribución gaussiana con media y covarianza. ${\ Displaystyle Av_ {0}}$${\ Displaystyle w \ in V}$

Esto se representa en la figura adjunta, donde las estructuras cerebrales subcorticales se representan en un sistema de coordenadas bidimensional basado en productos internos de sus campos vectoriales iniciales que los generan a partir de la plantilla que se muestra en un espacio bidimensional del espacio de Hilbert.

Estimación de plantilla a partir de poblaciones

El estudio de la forma y las estadísticas en las poblaciones son teorías locales, que indexan formas y estructuras a plantillas a las que se asignan biyectivamente. La forma estadística es entonces el estudio de correspondencias difeomórficas relativas a la plantilla. Una operación central es la generación de plantillas a partir de poblaciones, estimando una forma que se corresponda con la población. Existen varios métodos importantes para generar plantillas, incluidos métodos basados ​​en promedios de Frechet y enfoques estadísticos basados ​​en el algoritmo de maximización de expectativas y los modelos de órbita aleatoria de Bayes de anatomía computacional. En la figura adjunta se muestra una reconstrucción de la plantilla subcortical de la población de sujetos con resonancia magnética.

Software para mapeo difeomórfico

Las suites de software que contienen una variedad de algoritmos de mapeo difeomórfico incluyen lo siguiente:

• Hormigas
• Morfometría basada en vóxeles DARTEL
• DEFORMETRICA
• Demonios
• LDDMM Mapeo métrico difeomórfico de deformación grande
• LDDMM basado en kernel basado en marcos
• EstacionarioLDDMM

Software en la nube

• MRICloud

Ver también

• Estimación bayesiana de plantillas en anatomía computacional
• Neuroanatomía computacional
• Análisis de datos geométricos
• Mapeo métrico difeomórfico de gran deformación
• Análisis de procusto
• Métrica de Riemann y soporte de Lie en anatomía computacional
• Análisis de formas (desambiguación)
• Análisis estadístico de formas

Referencias