antiparalelogramo -Antiparallelogram
En geometría , un antiparalelogramo es un tipo de cuadrilátero autocruzado . Al igual que un paralelogramo , un antiparalelogramo tiene dos pares opuestos de lados de igual longitud, pero estos pares de lados no son en general paralelos. En cambio, los lados del par más largo se cruzan entre sí como en un mecanismo de tijera . Los antiparalelogramos también se llaman contraparalelogramos o paralelogramos cruzados .
Los antiparalelogramos ocurren como las figuras de vértice de ciertos poliedros uniformes no convexos . En la teoría de los eslabonamientos de cuatro barras , los eslabonamientos con forma de antiparalelogramo también se denominan eslabonamientos de mariposa o eslabonamientos de corbatín , y se utilizan en el diseño de engranajes no circulares . En mecánica celeste , se dan en ciertas familias de soluciones al problema de los 4 cuerpos .
Cada antiparalelogramo tiene un eje de simetría , con los cuatro vértices en un círculo. Se puede formar a partir de un trapezoide isósceles sumando las dos diagonales y eliminando dos lados paralelos. El área con signo de todo antiparalelogramo es cero.
Propiedades geométricas
Un antiparalelogramo es un caso especial de un cuadrilátero cruzado , con dos pares de aristas de igual longitud. En general, los cuadriláteros cruzados pueden tener bordes desiguales. Una forma especial del antiparalelogramo es un rectángulo cruzado , en el que dos bordes opuestos son paralelos. Cada antiparalelogramo es un cuadrilátero cíclico , lo que significa que sus cuatro vértices se encuentran todos en un solo círculo .
Todo antiparalelogramo tiene un eje de simetría que pasa por su punto de cruce. Debido a esta simetría, tiene dos pares de ángulos iguales y dos pares de lados iguales. Los cuatro puntos medios de sus lados están sobre una línea perpendicular al eje de simetría; es decir, para este tipo de cuadrilátero, el paralelogramo de Varignon es un cuadrilátero degenerado de área cero, que consta de cuatro puntos colineales. El casco convexo de un antiparalelogramo es un trapezoide isósceles , y cada antiparalelogramo puede formarse a partir de un trapezoide isósceles (o sus casos especiales, los rectángulos y cuadrados) reemplazando dos lados paralelos por las dos diagonales del trapezoide.
Debido a que un antiparalelogramo forma dos regiones triangulares congruentes del plano, pero gira alrededor de esas dos regiones en direcciones opuestas, su área con signo es la diferencia entre las áreas de las regiones y, por lo tanto, es cero. El área sin signo del polígono (el área total que rodea) es la suma, en lugar de la diferencia, de estas áreas. Para un antiparalelogramo con dos diagonales paralelas de longitud y , separadas por altura , esta suma es . De la aplicación de la desigualdad del triángulo a estas dos regiones triangulares se deduce que el par de aristas que se cruzan en un antiparalelogramo siempre debe ser más largo que las dos aristas que no se cruzan.
Aplicaciones
en poliedros
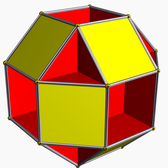
Varios poliedros uniformes no convexos , incluidos el tetrahemihexaedro , el cubohemioctaedro , el octahemioctaedro , el rombihexaedro pequeño , el icosihemidodecaedro pequeño y el dodecahemidodecaedro pequeño , tienen antiparalelogramos como figuras de vértice , las secciones transversales se forman cortando el poliedro por un plano que pasa cerca de un vértice, perpendicularmente a el eje entre el vértice y el centro.
Una forma de poliedro no uniforme pero flexible , el octaedro Bricard , se puede construir como una bipirámide sobre un antiparalelogramo.
Eslabonamientos de cuatro barras
El antiparalelogramo se ha utilizado como una forma de enlace de cuatro barras , en el que cuatro vigas rígidas de longitud fija (los cuatro lados del antiparalelogramo) pueden rotar entre sí en juntas colocadas en los cuatro vértices del antiparalelogramo. En este contexto también se le llama eslabón de mariposa o de pajarita . Como enlace, tiene un punto de inestabilidad en el que se puede convertir en un paralelogramo y viceversa, pero cualquiera de estos enlaces se puede arriostrar para evitar esta inestabilidad.
Tanto para los eslabonamientos de paralelogramo como de antiparalelogramo, si uno de los bordes largos (cruzados) del eslabonamiento se fija como base, las juntas libres se mueven en círculos iguales, pero en un paralelogramo se mueven en la misma dirección con velocidades iguales mientras que en el antiparalelogramo se mueven en direcciones opuestas con velocidades desiguales. Como descubrió James Watt , si un antiparalelogramo tiene su lado largo fijo de esta manera, el punto medio del borde largo no fijo trazará una lemniscata o una curva en forma de ocho. Para el antiparalelogramo formado por los lados y las diagonales de un cuadrado, es la lemniscata de Bernoulli .
El antiparalelogramo con su lado largo fijo es una variante del enlace de Watt . Un antiparalelogramo es una característica importante en el diseño del inversor de Hart , un enlace que (como el enlace de Peaucellier-Lipkin ) puede convertir el movimiento giratorio en movimiento rectilíneo. También se puede usar un enlace en forma de antiparalelogramo para conectar los dos ejes de un vehículo de cuatro ruedas, disminuyendo el radio de giro del vehículo en relación con una suspensión que solo permite girar un eje. Se usó un par de antiparalelogramos anidados en un enlace definido por Alfred Kempe como parte del Teorema de Universalidad de Kempe que establece que cualquier curva algebraica puede trazarse mediante las uniones de un enlace adecuadamente definido. Kempe llamó al enlace de antiparalelogramo anidado un "multiplicador", ya que podría usarse para multiplicar un ángulo por un número entero. Usado en la otra dirección, para dividir ángulos, puede usarse para la trisección de ángulos (aunque no como una regla y compás ). Las construcciones originales de Kempe que usaban este enlace pasaban por alto la inestabilidad del paralelogramo-antiparalelogramo, pero reforzar los enlaces arregla su prueba del teorema de universalidad.
Diseño de engranajes
Suponga que uno de los bordes cortos (no cruzados) de un eslabonamiento antiparalelogramo está fijo en su lugar y el eslabonamiento restante se mueve libremente. Por la simetría de los antiparalelogramos, cada uno de los dos segmentos de recta desde un punto extremo del borde fijo hasta el punto de cruce es congruente con un segmento de recta reflejado desde el punto de cruce hasta el segmento corto en movimiento, de lo cual se deduce que los dos segmentos desde el borde fijo tienen la misma longitud total que un solo borde largo. Debido a que el punto de cruce en movimiento mantiene una distancia total constante a los dos puntos finales del segmento fijo, traza una elipse que tiene los puntos finales del borde fijo como focos. Simétricamente, el otro borde corto móvil del antiparalelogramo tiene como puntos extremos los focos de otra elipse móvil, formada a partir de la primera por reflexión a través de una línea tangente a través del punto de cruce. Esta construcción de elipses a partir del movimiento de un antiparalelogramo se puede utilizar en el diseño de engranajes elípticos que convierten la rotación uniforme en rotación no uniforme o viceversa.
Mecánica celeste
En el problema de n -cuerpos , el estudio de los movimientos de masas puntuales bajo la ley de gravitación universal de Newton , las configuraciones centrales juegan un papel importante , soluciones al problema de n -cuerpos en los que todos los cuerpos giran alrededor de algún punto central como si estuvieran rígidamente conectados entre sí. Por ejemplo, para tres cuerpos hay cinco soluciones de este tipo, dadas por los cinco puntos de Lagrange . Para cuatro cuerpos, con dos pares de cuerpos que tienen masas iguales (pero con la relación entre las masas de los dos pares variando continuamente), la evidencia numérica indica que existe una familia continua de configuraciones centrales, relacionadas entre sí por el movimiento de un enlace antiparalelogramo.