Teorema del hexágono de Pappus - Pappus's hexagon theorem

Teorema del hexágono de Pappus: los puntos X , Y y Z son colineales en la línea de Pappus. El hexágono es AbCaBc .

Teorema de Pappus: forma afín
${\ Displaystyle Ab \ paralelo aB, Bc \ paralelo bC \ Flecha derecha Ac \ paralelo aC}$

En matemáticas, el teorema del hexágono de Pappus (atribuido a Pappus de Alejandría ) establece que

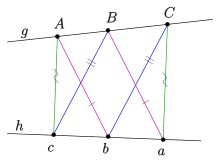
• dado un conjunto de colineales puntos , y otro conjunto de puntos colineales , a continuación, los puntos de intersección de la línea de pares y y y son colineales , tendido en el línea de Pappus . Estos tres puntos son los puntos de intersección de los lados "opuestos" del hexágono .${\ Displaystyle A, B, C}$${\ Displaystyle a, b, c}$${\ Displaystyle X, Y, Z}$${\ displaystyle Ab}$${\ Displaystyle aB, Ac}$${\ Displaystyle aC, Bc}$${\ Displaystyle bC}$${\ displaystyle AbCaBc}$

Se mantiene en un plano proyectivo sobre cualquier campo, pero falla para planos proyectivos sobre cualquier anillo de división no conmutativo . Los planos proyectivos en los que el "teorema" es válido se denominan planos papianos .

Si se restringe el plano proyectivo de manera que la línea de Pappus sea ​​la línea en el infinito, se obtiene la versión afín del teorema de Pappus que se muestra en el segundo diagrama. ${\ Displaystyle u}$

Si la línea de Pappus y las líneas tienen un punto en común, se obtiene la llamada versión pequeña del teorema de Pappus. ${\ Displaystyle u}$${\ Displaystyle g, h}$

El dual de esta incidencia teorema afirma que dado un conjunto de líneas concurrentes , y otro conjunto de líneas concurrentes , entonces las líneas definidas por pares de puntos resultantes de pares de intersecciones y y y son concurrentes. ( Concurrente significa que las líneas pasan por un punto). ${\ Displaystyle A, B, C}$${\ Displaystyle a, b, c}$${\ Displaystyle x, y, z}$${\ Displaystyle A \ cap b}$${\ Displaystyle a \ cap B, \; A \ cap c}$${\ Displaystyle a \ cap C, \; B \ cap c}$${\ Displaystyle b \ cap C}$

El teorema de Pappus es un caso especial del teorema de Pascal para una cónica, el caso límite cuando la cónica degenera en 2 líneas rectas. El teorema de Pascal es a su vez un caso especial del teorema de Cayley-Bacharach .

La configuración de Pappus es la configuración de 9 líneas y 9 puntos que ocurre en el teorema de Pappus, donde cada línea se encuentra con 3 de los puntos y cada punto se encuentra con 3 líneas. En general, la línea de Pappus no pasa por el punto de intersección de y . Esta configuración es auto dual . Dado que, en particular, las líneas tienen las propiedades de las líneas del teorema dual, y la colinealidad de es equivalente a la concurrencia de , el teorema dual es, por lo tanto, exactamente igual que el teorema mismo. El gráfico de Levi de la configuración de Pappus es el gráfico de Pappus , un gráfico bipartito de distancia regular con 18 vértices y 27 aristas. ${\ Displaystyle ABC}$${\ displaystyle abc}$${\ Displaystyle Bc, bC, XY}$${\ Displaystyle x, y, z}$${\ Displaystyle X, Y, Z}$${\ Displaystyle Bc, bC, XY}$

Prueba: forma afín

Teorema de Pappus: demostración

Si se puede probar la forma afín del enunciado, entonces se prueba la forma proyectiva del teorema de Pappus, ya que la extensión de un plano papiano a un plano proyectivo es única.

Debido a la paralelismo en un plano afín, uno tiene que distinguir dos casos: y . La clave para una demostración simple es la posibilidad de introducir un sistema de coordenadas "adecuado": ${\ Displaystyle g \ not \ paralelo h}$${\ Displaystyle g \ paralelo h}$

Caso 1: Las líneas se cruzan en un punto . En este caso se introducen coordenadas, tal que (ver diagrama). tener las coordenadas . ${\ Displaystyle g, h}$${\ Displaystyle S = g \ cap h}$
${\ Displaystyle \; S = (0,0), \; A = (0,1), \; c = (1,0) \;}$${\ Displaystyle B, C}$${\ Displaystyle \; B = (0, \ gamma), \; C = (0, \ delta), \; \ gamma, \ delta \ notin \ {0,1 \}}$

De la paralelidad de las líneas se obtiene y la paralelidad de las líneas cede . Por tanto, la recta tiene pendiente y es una recta paralela . ${\ Displaystyle Bc, \; Cb}$${\ Displaystyle b = ({\ tfrac {\ delta} {\ gamma}}, 0)}$${\ displaystyle Ab, Ba}$${\ Displaystyle a = (\ delta, 0)}$${\ Displaystyle Ca}$${\ Displaystyle -1}$${\ displaystyle Ac}$

Caso 2: (pequeño teorema). En este caso, las coordenadas se eligen de tal manera que . De la paralelismo de y se obtiene y , respectivamente, y al menos la paralelismo . ${\ Displaystyle g \ paralelo h \}$
${\ Displaystyle \; c = (0,0), \; b = (1,0), \; A = (0,1), \; B = (\ gamma, 1), \; \ gamma \ neq 0}$${\ Displaystyle Ab \ paralelo Ba}$${\ Displaystyle cB \ paralelo bC}$${\ Displaystyle \; C = (\ gamma +1,1) \;}$${\ Displaystyle \; a = (\ gamma +1,0) \;}$${\ Displaystyle \; Ac \ paralelo Ca \;}$

Prueba con coordenadas homogéneas

Elija coordenadas homogéneas con

${\ Displaystyle C = (1,0,0), \; c = (0,1,0), \; X = (0,0,1), \; A = (1,1,1)}$.

En las líneas , dadas por , tome los puntos como ${\ Displaystyle AC, Ac, AX}$${\ Displaystyle x_ {2} = x_ {3}, \; x_ {1} = x_ {3}, \; x_ {2} = x_ {1}}$${\ Displaystyle B, Y, b}$

${\ Displaystyle B = (p, 1,1), \; Y = (1, q, 1), \; b = (1,1, r)}$

para algunos . Las tres líneas son , por lo que pasan por el mismo punto si y solo si . La condición para que las tres líneas y con ecuaciones pasen por el mismo punto es . Entonces, este último conjunto de tres líneas es concurrente si los otros ocho conjuntos son porque la multiplicación es conmutativa, entonces . De manera equivalente, son colineales. ${\ Displaystyle p, q, r}$${\ Displaystyle XB, CY, cb}$${\ Displaystyle x_ {1} = x_ {2} p, \; x_ {2} = x_ {3} q, \; x_ {3} = x_ {1} r}$${\ Displaystyle a}$${\ displaystyle rqp = 1}$${\ Displaystyle Cb, cB}$${\ Displaystyle XY}$${\ Displaystyle x_ {2} = x_ {1} q, \; x_ {1} = x_ {3} p, \; x_ {3} = x_ {2} r}$${\ Displaystyle Z}$${\ displaystyle rpq = 1}$${\ Displaystyle pq = qp}$${\ Displaystyle X, Y, Z}$

La demostración anterior también muestra que para que el teorema de Pappus sea válido para un espacio proyectivo sobre un anillo de división, es suficiente y necesario que el anillo de división sea un campo (conmutativo). El matemático alemán Gerhard Hessenberg demostró que el teorema de Pappus implica el teorema de Desargues . En general, el teorema de Pappus es válido para algún plano proyectivo si y solo si es un plano proyectivo sobre un campo conmutativo. Los aviones descriptivos en los que el teorema de Pappus no posee son Desarguesian aviones descriptivos más anillos de división no conmutativos, y planos no Desarguesian .

La prueba no es válida si resulta ser colineal. En ese caso, se puede proporcionar una prueba alternativa, por ejemplo, utilizando una referencia proyectiva diferente. ${\ Displaystyle C, c, X}$

Teorema dual

Debido al principio de dualidad para planos proyectivos, el teorema dual de Pappus es verdadero:

Si se eligen 6 líneas alternativamente de dos lápices con centros , las líneas ${\ Displaystyle A, b, C, a, B, c}$${\ Displaystyle G, H}$

${\ Displaystyle X: = (A \ cap b) (a \ cap B),}$

${\ Displaystyle Y: = (c \ cap A) (C \ cap a),}$

${\ Displaystyle Z: = (b \ cap C) (B \ cap c)}$

son concurrentes, es decir: tienen un punto en común. El diagrama de la izquierda muestra la versión proyectiva, el de la derecha una versión afín, donde los puntos son puntos en el infinito. Si el punto está en la línea, entonces se obtiene el "pequeño teorema dual" del teorema de Pappus. ${\ Displaystyle U}$
${\ Displaystyle G, H}$${\ Displaystyle U}$${\ displaystyle GH}$

• 

  teorema dual: forma proyectiva

• 

  teorema dual: forma afín

Si en la versión afín del "pequeño teorema" dual el punto también es un punto en el infinito, se obtiene el teorema de Thomsen , un enunciado sobre 6 puntos en los lados de un triángulo (ver diagrama). La figura de Thomsen juega un papel fundamental coordinando un plano proyectivo definido axiomático. La prueba del cierre de la figura de Thomsen está cubierta por la prueba del "pequeño teorema", dada anteriormente. Pero también existe una prueba directa simple: ${\ Displaystyle U}$

Debido a que el enunciado del teorema de Thomsen (el cierre de la figura) usa solo los términos conectar, intersectar y paralelo , el enunciado es afinamente invariante y se pueden introducir coordenadas tales que (ver diagrama de la derecha). El punto de partida de la secuencia de acordes es. Uno verifica fácilmente las coordenadas de los puntos dados en el diagrama, que muestra: el último punto coincide con el primer punto. ${\ Displaystyle P = (0,0), \; Q = (1,0), \; R = (0,1)}$${\ displaystyle (0, \ lambda).}$

• 

  La figura de Thomsen (puntos del triángulo ) como teorema dual del pequeño teorema de Pappus (¡también está en el infinito!). ${\ Displaystyle \ color {rojo} 1,2,3,4,5,6}$${\ displaystyle PQR}$${\ Displaystyle U}$

• 

  Figura de Thomsen: prueba

Otras declaraciones del teorema

Triángulos y son perspectiva desde y , y así, también desde .${\ displaystyle XcC}$${\ Displaystyle BbY}$${\ Displaystyle A}$${\ Displaystyle a}$${\ Displaystyle Z}$

Además de las caracterizaciones anteriores del teorema de Pappus y su dual, las siguientes son declaraciones equivalentes:

• Si los seis vértices de un hexágono se encuentran alternativamente en dos líneas, entonces los tres puntos de intersección de pares de lados opuestos son colineales.
• Organizados en una matriz de nueve puntos (como en la figura y descripción de arriba) y pensados ​​como la evaluación de un permanente , si las dos primeras filas y las seis tríadas "diagonales" son colineales, entonces la tercera fila es colineal.

${\ Displaystyle \ left | {\ begin {matrix} A & B & C \\ a & b & c \\ X & Y & Z \ end {matrix}} \ right |}$

Es decir, si son líneas, entonces el teorema de Pappus establece que debe ser una línea. Además, tenga en cuenta que la misma formulación matricial se aplica a la forma dual del teorema cuando, etc., son triples de líneas concurrentes.${\ Displaystyle \ ABC, abc, AbZ, BcX, CaY, XbC, YcA, ZaB \}$${\ displaystyle XYZ}$${\ Displaystyle (A, B, C)}$

• Dados tres puntos distintos en cada una de dos líneas distintas, empareje cada punto en una de las líneas con uno de la otra línea, luego las uniones de puntos no emparejados se encontrarán en pares (opuestos) en puntos a lo largo de una línea.
• Si dos triángulos tienen perspectiva de al menos dos formas diferentes, entonces son perspectiva de tres formas.
• Si y son concurrentes y y son concurrentes, entonces y son concurrentes.${\ Displaystyle \; AB, CD, \;}$${\ displaystyle EF}$${\ displaystyle DE, FA,}$${\ Displaystyle BC}$${\ displaystyle AD, BE,}$${\ Displaystyle CF}$

Orígenes

En su forma más antigua conocida, el Teorema de Pappus son las Proposiciones 138, 139, 141 y 143 del Libro VII de la Colección de Pappus . Estos son Lemmas XII, XIII, XV, XVII y en la parte del libro VII consiste en lemas para el primero de los tres libros de Euclides 's Porismas.

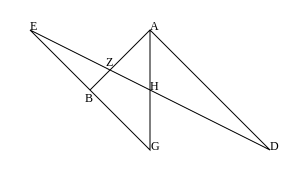
Los lemas se prueban en términos de lo que hoy se conoce como la relación cruzada de cuatro puntos colineales. Se utilizan tres lemas anteriores. El primero de ellos, Lema III, tiene el siguiente diagrama (que usa las letras de Pappus, con G para Γ, D para Δ, J para Θ y L para Λ).

Aquí tres líneas rectas concurrentes, AB, AG y AD, están cruzadas por dos líneas, JB y JE, que concurren en J. También KL se dibuja paralela a AZ. Luego

KJ: JL :: (KJ: AG y AG: JL) :: (JD: GD y BG: JB).

Estas proporciones podrían escribirse hoy como ecuaciones:

KJ / JL = (KJ / AG) (AG / JL) = (JD / GD) (BG / JB).

La última relación compuesta (a saber, JD: GD y BG: JB) es lo que se conoce hoy como la relación cruzada de los puntos colineales J, G, D y B en ese orden; hoy se denota por (J, G; D, B). Así que hemos demostrado que esto es independiente de la elección de la línea recta particular JD que cruza las tres líneas rectas que concurren en A. En particular

(J, G; D, B) = (J, Z; H, E).

No importa de qué lado de A caiga la línea recta JE. En particular, la situación puede ser como en el siguiente diagrama, que es el diagrama del Lema X.

Al igual que antes, tenemos (J, G; D, B) = (J, Z; H, E). Pappus no prueba esto explícitamente; pero el Lema X es inverso, es decir, que si estas dos relaciones cruzadas son iguales y las líneas rectas BE y DH se cruzan en A, entonces los puntos G, A y Z deben ser colineales.

Lo que mostramos originalmente se puede escribir como (J, ∞; K, L) = (J, G; D, B), con ∞ tomando el lugar de la intersección (inexistente) de JK y AG. Pappus muestra esto, en efecto, en el Lema XI, cuyo diagrama, sin embargo, tiene letras diferentes:

Lo que muestra Pappus es DE.ZH: EZ.HD :: GB: BE, que podemos escribir como

(D, Z; E, H) = (∞, B; E, G).

El diagrama del Lema XII es:

El diagrama para el Lema XIII es el mismo, pero BA y DG, extendidos, se encuentran en N.En cualquier caso, considerando las líneas rectas que atraviesan G como cortadas por las tres líneas rectas que atraviesan A, (y aceptando que las ecuaciones de relaciones cruzadas siguen siendo válidas después de permutación de las entradas,) tenemos por Lema III o XI

(G, J; E, H) = (G, D; ∞ Z).

Considerando las líneas rectas que atraviesan D como cortadas por las tres líneas rectas que atraviesan B, tenemos

(L, D; E, K) = (G, D; ∞ Z).

Por lo tanto (E, H; J, G) = (E, K; D, L), por lo que según el Lema X, los puntos H, M y K son colineales. Es decir, los puntos de intersección de los pares de lados opuestos del hexágono ADEGBZ son colineales.

Los lemas XV y XVII son que, si el punto M se determina como la intersección de HK y BG, entonces los puntos A, M y D son colineales. Es decir, los puntos de intersección de los pares de lados opuestos del hexágono BEKHZG son colineales.

Notas

Referencias

• Coxeter, Harold Scott MacDonald (1969), Introducción a la geometría (2a ed.), Nueva York: John Wiley & Sons , ISBN 978-0-471-50458-0, MR  0123930
• Cronheim, A. (1953), "Una prueba del teorema de Hessenberg", Proceedings of the American Mathematical Society , 4 (2): 219-221, doi : 10.2307 / 2031794 , JSTOR  2031794
• Dembowski, Peter (1968), Geometrías finitas , Berlín: Springer Verlag
• Heath, Thomas (1981) [1921], A History of Greek Mathematics , Nueva York: Dover
• Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen , Berlín / Heidelberg: Springer, 61 (2): 161-172, doi : 10.1007 / BF01457558 , ISSN  1432-1807
• Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt , Berlín
• Kline, Morris (1972), Pensamiento matemático desde tiempos antiguos a tiempos modernos , Nueva York: Oxford University Press
• Pambuccian, Victor; Schacht, Celia (2019), "El destino axiomático de los teoremas de Pappus y Desargues", en Dani, SG; Papadopoulos, A. (eds.), Geometry in history , Springer, págs. 355–399, ISBN 978-3-030-13611-6
• Whicher, Olive (1971), Geometría proyectiva , Rudolph Steiner Press, ISBN 0-85440-245-4

enlaces externos

• Teorema del hexágono de Pappus en cortar el nudo
• Dual al teorema del hexágono de Pappus en cortar el nudo
• Teorema de Pappus: nueve demostraciones y tres variaciones