Polígono de Newton - Newton polygon

Construcción del polígono de Newton del polinomio con respecto a la valoración 5-ádica.

{\ Displaystyle P (X) = 1 + 5X + 1 / 5X ^ {2} + 35X ^ {3} + 25X ^ {5} + 625X ^ {6}}

En matemáticas , el polígono de Newton es una herramienta para comprender el comportamiento de polinomios sobre campos locales .

En el caso original, el campo de interés local era el campo de la serie formal de Laurent en la X indeterminada , es decir, el campo de fracciones del anillo formal de la serie de poder.

K [[X]],

sobre K , donde K era el número real o el campo de números complejos . Esto sigue siendo de considerable utilidad con respecto a las expansiones de Puiseux . El polígono de Newton es un dispositivo eficaz para comprender los términos principales

aX ^r

de las soluciones de expansión de la serie de potencias a las ecuaciones

P ( F ( X )) = 0

donde P es un polinomio con coeficientes en K [ X ], el anillo polinomial ; es decir, funciones algebraicas implícitamente definidas . Los exponentes r aquí son ciertos números racionales , dependiendo de la rama elegida; y las soluciones en sí son series de potencia en

K [[Y]]

con Y = X ^{1 / d} para un denominador d correspondiente a la rama. El polígono de Newton ofrece un método algorítmico eficaz para calcular d .

Después de la introducción de los números p-ádicos , se demostró que el polígono de Newton es igualmente útil en cuestiones de ramificación para campos locales y, por tanto, en la teoría algebraica de números . Los polígonos de Newton también han sido útiles en el estudio de curvas elípticas .

Definición

A priori, dado un polinomio sobre un campo, el comportamiento de las raíces (asumiendo que tiene raíces) será desconocido. Los polígonos de Newton proporcionan una técnica para el estudio del comportamiento de las raíces.

Sea un campo local con valoración discreta y sea ${\ Displaystyle K}$ ${\ Displaystyle v_ {K}}$

{\ Displaystyle f (x) = a_ {n} x ^ {n} + \ cdots + a_ {1} x + a_ {0} \ in K [x]}

con . Entonces el polígono de Newton de se define como el casco convexo inferior del conjunto de puntos ${\ Displaystyle a_ {0} a_ {n} \ neq 0}$ ${\ Displaystyle f}$

{\ Displaystyle P_ {i} = \ left (i, v_ {K} (a_ {i}) \ right),}

ignorando los puntos con . Reformulado geométricamente, grafique todos estos puntos P _i en el plano xy . Supongamos que los índices de puntos aumentan de izquierda a derecha ( P ₀ es el punto más a la izquierda, P _n es el punto más a la derecha). Luego, comenzando en P ₀ , dibuje un rayo hacia abajo paralelo al eje y , y rote este rayo en sentido antihorario hasta que llegue al punto P _k_₁ (no necesariamente P ₁ ). Rompe el rayo aquí. Ahora dibuje un segundo rayo desde P _k_₁ recto hacia abajo paralelo con el eje y , y gire este rayo en sentido antihorario hasta que llegue al punto P _k_₂ . Continuar hasta que el proceso alcance el punto P _n ; el polígono resultante (que contiene los puntos P ₀ , P _k_₁ , P _k_₂ , ..., P _k_{_m} , P _n ) es el polígono de Newton. ${\ Displaystyle a_ {i} = 0}$

Otra forma, quizás más intuitiva, de ver este proceso es la siguiente: considere una banda elástica que rodea todos los puntos P ₀ , ..., P _n . Estire la banda hacia arriba, de manera que la banda quede pegada en su lado inferior por algunos de los puntos (los puntos actúan como clavos, parcialmente clavados en el plano xy). Los vértices del polígono de Newton son exactamente esos puntos.

Para obtener un diagrama detallado de esto, consulte el capítulo 6 § 3 de "Campos locales" de JWS Cassels, LMS Student Texts 3, CUP 1986. Está en la p99 de la edición de bolsillo de 1986.

Historia

Los polígonos de Newton llevan el nombre de Isaac Newton , quien los describió por primera vez y algunos de sus usos en la correspondencia del año 1676 dirigida a Henry Oldenburg .

Aplicaciones

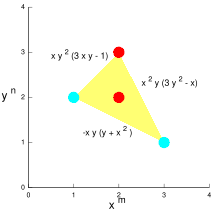
Un polígono de Newton es a veces un caso especial de un politopo de Newton y se puede utilizar para construir soluciones asintóticas de ecuaciones polinómicas de dos variables como ${\ Displaystyle 3x ^ {2} y ^ {3} -xy ^ {2} + 2x ^ {2} y ^ {2} -x ^ {3} y = 0}$

Este diagrama muestra el polígono de Newton para P ( x , y ) = 3 x ² y ³ - xy ² + 2 x ²y ² - x ³y , con monomios positivos en rojo y monomios negativos en cian. Las caras están etiquetadas con los términos limitantes a los que corresponden.

Otra aplicación del polígono de Newton proviene del siguiente resultado:

Dejar

{\ Displaystyle \ mu _ {1}, \ mu _ {2}, \ ldots, \ mu _ {r}}

ser las pendientes de los segmentos de recta del polígono de Newton de (como se definió anteriormente) dispuestos en orden creciente, y sea ${\ Displaystyle f (x)}$

{\ Displaystyle \ lambda _ {1}, \ lambda _ {2}, \ ldots, \ lambda _ {r}}

ser las longitudes correspondientes de los segmentos de línea proyectados sobre el eje x (es decir, si tenemos un segmento de línea que se extiende entre los puntos y entonces la longitud es ). Luego, para cada número entero , tiene exactamente raíces con valoración . ${\ Displaystyle P_ {i}}$ ${\ Displaystyle P_ {j}}$ ${\ displaystyle ji}$ ${\ Displaystyle 1 \ leq \ kappa \ leq r}$ ${\ Displaystyle f (x)}$ ${\ Displaystyle \ lambda _ {\ kappa}}$ ${\ Displaystyle - \ mu _ {\ kappa}}$

Explicación de la función simétrica

En el contexto de una valoración, se nos da cierta información en forma de valoraciones de funciones simétricas elementales de las raíces de un polinomio, y requerimos información sobre las valoraciones de las raíces reales, en un cierre algebraico . Esto tiene aspectos tanto de la teoría de la ramificación y la teoría de la singularidad . Las inferencias válidas posibles son las valoraciones de sumas de potencia , mediante las identidades de Newton .

Ver también

Referencias

Goss, David (1996), Estructuras básicas de aritmética de campos funcionales , Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Resultados en matemáticas y áreas relacionadas (3)], 35 , Berlín, Nueva York: Springer-Verlag , doi : 10.1007 / 978-3-642-61480-4 , ISBN 978-3-540-61087-8, MR 1423131
Gouvêa, Fernando : números p-ádicos: una introducción. Springer Verlag 1993. pág. 199.

enlaces externos

Applet dibujando un polígono de Newton

Languages

In other projects