Curva matemática construida a partir de otra curva

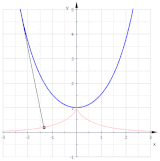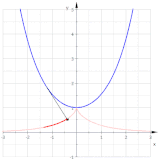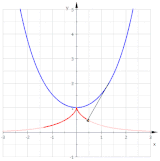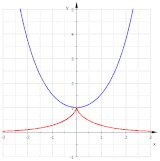
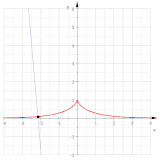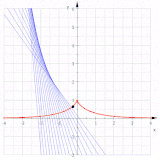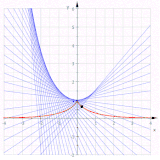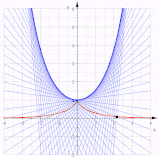
Dos involutas (rojo) de una parábola
En matemáticas , una involuta (también conocida como evolutiva ) es un tipo particular de curva que depende de otra forma o curva. Una involuta de una curva es el lugar de un punto en un trozo de cuerda tensa cuando la cuerda se desenvuelve o se enrolla alrededor de la curva.
Es una clase de curvas que pertenecen a la familia de curvas de la ruleta .
La evoluta de una involuta es la curva original.
Las nociones de involuta y evoluta de una curva fueron introducidas por Christiaan Huygens en su obra titulada Horologium oscillatorium sive de motu pendulorum ad horologia aptato demostrationes geometricae (1673).
Involuta de una curva parametrizada
Sea una curva regular en el plano con su curvatura en ninguna parte 0 y , luego, la curva con la representación paramétrica
![{\ Displaystyle {\ vec {c}} (t), \; t \ in [t_ {1}, t_ {2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b014b9d8601fa970d2eaa1f8132f2f34ec432233)


es una involuta de la curva dada.
Prueba
La cuerda actúa como tangente a la curva . Su longitud cambia en una cantidad igual a la longitud del arco atravesado mientras se enrolla o desenrolla. La longitud del arco de la curva atravesada en el intervalo está dada por
 ![{\ Displaystyle [a, t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7e4d6424116f83d1d8eadea305b1ccc9c8744e) 
donde es el punto de partida desde donde se mide la longitud del arco. Dado que el vector tangente representa la cuerda tensa aquí, obtenemos el vector de cuerda como


El vector correspondiente al punto final de la cadena ( ) se puede calcular fácilmente mediante la suma de vectores , y se obtiene


|
Agregar un número arbitrario pero fijo a la integral da como resultado una involuta correspondiente a una cuerda extendida por (como una bola de hilo de lana que ya tiene un trozo de hilo colgando antes de desenrollarse). Por lo tanto, la involuta se puede variar por constante y / o agregando un número a la integral (ver Involutos de una parábola semicúbica ).




Si uno consigue


Propiedades de las involutas

Involuto: propiedades. Los ángulos representados son de 90 grados.
Para derivar las propiedades de una curva regular es ventajoso suponer que la longitud del arco es el parámetro de la curva dada, lo que conduce a las siguientes simplificaciones: y , con la curvatura y la unidad normal. Se obtiene por la involuta:





-
 y
y

y la declaración:
- En el punto la involuta no es regular (porque ),


y de lo siguiente:

- La normal de la involuta en el punto es la tangente de la curva dada en el punto .


- Las involutas son curvas paralelas , debido al hecho de que es la unidad normal en .



Ejemplos
Involutos de un círculo
Para un círculo con representación paramétrica , se tiene
. Por lo tanto , y la longitud del camino es .




Al evaluar la ecuación dada anteriormente de la involuta, se obtiene

para la ecuación paramétrica de la involuta del círculo.
El término es opcional; sirve para establecer la ubicación inicial de la curva en el círculo. La figura muestra involutas para (verde), (rojo), (violeta) y (azul claro). Las involutas parecen espirales de Arquímedes , pero en realidad no lo son.





La longitud del arco para y de la involuta es




Involutos de una parábola semicúbica (azul). Solo la curva roja es una parábola.
Involutos de una parábola semicúbica
La ecuación paramétrica describe una parábola semicúbica . De uno obtiene y . Extender la cadena simplifica enormemente los cálculos adicionales, y se obtiene






Eliminando t se obtiene que muestra que esta involuta es una parábola .

Las otras involutas son así curvas paralelas de una parábola y no son parábolas, ya que son curvas de grado seis (Ver Curva paralela § Más ejemplos ).

La involuta roja de una catenaria (azul) es una tractriz.
Involutos de una catenaria
Para la catenaria , el vector tangente es , y, como su longitud . Por tanto, la longitud del arco desde el punto (0, 1) es 




Por tanto, la involuta a partir de (0, 1) está parametrizada por

y es por tanto una tractriz .
Las otras involutas no son tractrices, ya que son curvas paralelas de una tractriz.
Involutos de una cicloide

Involutos de una cicloide (azul): solo la curva roja es otra cicloide
La representación paramétrica describe una cicloide . De , se obtiene (después de haber usado algunas fórmulas trigonométricas)



y

Por tanto, las ecuaciones de la involuta correspondiente son


que describen la cicloide roja desplazada del diagrama. Por lo tanto
- Las involutas de la cicloide son curvas paralelas de la cicloide.


(Las curvas paralelas de una cicloide no son cicloides).
Involuta y evoluta
La evolución de una curva dada consta de los centros de curvatura de . Entre involutas y evolutas se cumple la siguiente afirmación:


- Una curva es la evolución de cualquiera de sus involutas.
Tractrix (rojo) como involuta de una catenaria
La evoluta de una tractriz es una catenaria
Solicitud
La involuta tiene algunas propiedades que la hacen extremadamente importante para la industria de engranajes : si dos engranajes entrelazados tienen dientes con la forma de perfil de involutas (en lugar de, por ejemplo, una forma triangular tradicional), forman un sistema de engranajes involutas . Sus velocidades relativas de rotación son constantes mientras los dientes están enganchados. Los engranajes también siempre hacen contacto a lo largo de una única línea de fuerza constante. Con dientes de otras formas, las velocidades y fuerzas relativas aumentan y disminuyen a medida que los dientes sucesivos se acoplan, lo que genera vibración, ruido y desgaste excesivo. Por esta razón, casi todos los dientes de engranajes modernos tienen la forma evolvente.

Mecanismo de un compresor scroll
La involuta de un círculo también es una forma importante en la compresión de gas , ya que se puede construir un compresor de espiral basándose en esta forma. Los compresores scroll hacen menos ruido que los compresores convencionales y han demostrado ser bastante eficientes .
El reactor de isótopos de alto flujo utiliza elementos combustibles en forma de involuta, ya que estos permiten un canal de ancho constante entre ellos para el refrigerante.
Ver también
Referencias
enlaces externos


![{\ Displaystyle {\ vec {c}} (t), \; t \ in [t_ {1}, t_ {2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b014b9d8601fa970d2eaa1f8132f2f34ec432233)



![{\ Displaystyle [a, t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7e4d6424116f83d1d8eadea305b1ccc9c8744e)