Método de Horner - Horner's method

En matemáticas e informática , el método de Horner (o el esquema de Horner ) es un algoritmo para la evaluación de polinomios . Aunque lleva el nombre de William George Horner , este método es mucho más antiguo, ya que el propio Horner lo atribuyó a Joseph-Louis Lagrange , y se remonta a muchos cientos de años hasta los matemáticos chinos y persas. Después de la introducción de las computadoras, este algoritmo se convirtió en fundamental para la computación eficiente con polinomios.

El algoritmo se basa en la regla de Horner:

${\ Displaystyle {\ begin {alineado} a_ {0} & + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n} \\ & = a_ {0} + x {\ bigg (} a_ {1} + x {\ Big (} a_ {2} + x {\ big (} a_ {3} + \ cdots + x ( a_ {n-1} + x \, a_ {n}) \ cdots {\ big)} {\ Big)} {\ bigg)}. \ end {alineado}}}$

Esto permite la evaluación de un polinomio de grado n con solo multiplicaciones y adiciones. Esto es óptimo, ya que hay polinomios de grado n que no se pueden evaluar con menos operaciones aritméticas. ${\ Displaystyle n}$${\ Displaystyle n}$

Alternativamente, el método de Horner también se refiere a un método para aproximar las raíces de polinomios, descrito por Horner en 1819. Es una variante del método de Newton-Raphson que se hizo más eficiente para el cálculo manual mediante la aplicación de la regla de Horner. Fue ampliamente utilizado hasta que las computadoras se generalizaron alrededor de 1970.

Evaluación polinomial y división larga.

Dado el polinomio

${\ Displaystyle p (x) = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n},}$

donde son coeficientes constantes, el problema es evaluar el polinomio en un valor específico de${\ Displaystyle a_ {0}, \ ldots, a_ {n}}$${\ Displaystyle x_ {0}}$${\ Displaystyle x.}$

Para ello, se define de forma recursiva una nueva secuencia de constantes de la siguiente manera:

${\ Displaystyle {\ begin {alineado} b_ {n} &: = a_ {n} \\ b_ {n-1} &: = a_ {n-1} + b_ {n} x_ {0} \\ (1 ) \ quad \ quad \ quad & ~~~ \ vdots \\ b_ {1} &: = a_ {1} + b_ {2} x_ {0} \\ b_ {0} &: = a_ {0} + b_ {1} x_ {0}. \ End {alineado}}}$

Entonces es el valor de . ${\ Displaystyle b_ {0}}$${\ Displaystyle p (x_ {0})}$

Para ver por qué funciona esto, el polinomio se puede escribir en la forma

${\ Displaystyle p (x) = a_ {0} + x {\ bigg (} a_ {1} + x {\ Big (} a_ {2} + x {\ big (} a_ {3} + \ cdots + x) (a_ {n-1} + x \, a_ {n}) \ cdots {\ big)} {\ Big)} {\ bigg)} \.}$

Por lo tanto, sustituyendo iterativamente el en la expresión, ${\ Displaystyle b_ {i}}$

${\ Displaystyle {\ begin {alineado} p (x_ {0}) & = a_ {0} + x_ {0} {\ Big (} a_ {1} + x_ {0} {\ big (} a_ {2}) + \ cdots + x_ {0} (a_ {n-1} + b_ {n} x_ {0}) \ cdots {\ big)} {\ Big)} \\ & = a_ {0} + x_ {0} {\ Big (} a_ {1} + x_ {0} {\ big (} a_ {2} + \ cdots + x_ {0} b_ {n-1} {\ big)} {\ Big)} \\ & ~~ \ vdots \\ & = a_ {0} + x_ {0} b_ {1} \\ & = b_ {0}. \ end {alineado}}}$

Ahora, se puede probar que;

${\ Displaystyle (2) \ quad \ quad \ quad p (x) = (b_ {1} + b_ {2} x + b_ {3} x ^ {2} + b_ {4} x ^ {3} + \ cdots + b_ {n-1} x ^ {n-2} + b_ {n} x ^ {n-1}) (x-x_ {0}) + b_ {0}}$

Esta expresión constituye la aplicación práctica de Horner, ya que ofrece una forma muy rápida de determinar el resultado de;

${\ Displaystyle p (x) / (x-x_ {0})}$

siendo b ₀ (que es igual ap (x ₀ )) el resto de la división, como se demuestra en los ejemplos siguientes. si x ₀ es una raíz de p (x), entonces b ₀ = 0 (lo que significa que el resto es 0), lo que significa que puede factorizar p (x) con (xx ₀ ).
En cuanto a encontrar los valores b consecutivos, comienza con la determinación de b _n , que es simplemente igual a a _n . Luego avanza hacia las otras b, usando la fórmula;

${\ Displaystyle b_ {n-1} = a_ {n-1} + b_ {n} x_ {0}}$

hasta llegar a b ₀ .

Ejemplos de

Evaluar para${\ Displaystyle f (x) = 2x ^ {3} -6x ^ {2} + 2x-1}$${\ Displaystyle x = 3.}$

Usamos la división sintética de la siguiente manera:

 x0│   x3    x2    x1    x0
 3 │   2    −6     2    −1
   │         6     0     6
   └────────────────────────
       2     0     2     5

Las entradas de la tercera fila son la suma de las de las dos primeras. Cada entrada en la segunda fila es el producto del valor x (3 en este ejemplo) con la entrada de la tercera fila inmediatamente a la izquierda. Las entradas de la primera fila son los coeficientes del polinomio a evaluar. Entonces el resto de la división entre es 5. ${\ Displaystyle f (x)}$${\ Displaystyle x-3}$

Pero por el teorema del residuo polinomial , sabemos que el residuo es . Por lo tanto${\ Displaystyle f (3)}$${\ Displaystyle f (3) = 5}$

En este ejemplo, si podemos ver eso , las entradas en la tercera fila. Entonces, la división sintética se basa en el método de Horner. ${\ Displaystyle a_ {3} = 2, a_ {2} = - 6, a_ {1} = 2, a_ {0} = - 1}$${\ Displaystyle b_ {3} = 2, b_ {2} = 0, b_ {1} = 2, b_ {0} = 5}$

Como consecuencia del teorema del resto del polinomio, las entradas de la tercera fila son los coeficientes del polinomio de segundo grado, el cociente de una división por . El resto es 5. Esto hace que el método de Horner sea útil para la división larga de polinomios . ${\ Displaystyle f (x)}$${\ Displaystyle x-3}$

Dividir por : ${\ Displaystyle x ^ {3} -6x ^ {2} + 11x-6}$${\ Displaystyle x-2}$

 2 │   1    −6    11    −6
   │         2    −8     6
   └────────────────────────
       1    −4     3     0

El cociente es . ${\ displaystyle x ^ {2} -4x + 3}$

Deja y . Dividir por usando el método de Horner. ${\ Displaystyle f_ {1} (x) = 4x ^ {4} -6x ^ {3} + 3x-5}$${\ Displaystyle f_ {2} (x) = 2x-1}$${\ Displaystyle f_ {1} (x)}$${\ Displaystyle f_ {2} \, (x)}$

  0.5 │ 4  -6   0   3  -5
      │     2  -2  -1   1
└───────────────────────
        2  -2  -1   1  -2

La tercera fila es la suma de las dos primeras filas, dividida por 2. Cada entrada de la segunda fila es el producto de 1 con la entrada de la tercera fila a la izquierda. La respuesta es

${\ Displaystyle {\ frac {f_ {1} (x)} {f_ {2} (x)}} = 2x ^ {3} -2x ^ {2} -x + 1 - {\ frac {4} {2x -1}}.}$

Eficiencia

La evaluación utilizando la forma monomial de un polinomio de grado n requiere como máximo n adiciones y ( n ²  +  n ) / 2 multiplicaciones, si las potencias se calculan mediante multiplicación repetida y cada monomio se evalúa individualmente. (Esto se puede reducir a n adiciones y 2 n  - 1 multiplicaciones evaluando las potencias de x de forma iterativa). Si los datos numéricos se representan en términos de dígitos (o bits), entonces el algoritmo ingenuo también implica almacenar aproximadamente 2 n veces el número. de bits de x (el polinomio evaluado tiene una magnitud aproximada x ⁿ , y también se debe almacenar x ⁿ ). Por el contrario, el método de Horner requiere solo n adiciones yn multiplicaciones, y sus requisitos de almacenamiento son solo n veces el número de bits de x . Alternativamente, el método de Horner se puede calcular con n multiplicaciones-adiciones fusionadas . El método de Horner también se puede extender para evaluar las primeras k derivadas del polinomio con kn adiciones y multiplicaciones.

El método de Horner es óptimo, en el sentido de que cualquier algoritmo para evaluar un polinomio arbitrario debe utilizar al menos la misma cantidad de operaciones. Alexander Ostrowski demostró en 1954 que el número de adiciones necesarias es mínimo. Victor Pan demostró en 1966 que el número de multiplicaciones es mínimo. Sin embargo, cuando x es una matriz, el método de Horner no es óptimo .

Esto supone que el polinomio se evalúa en forma monomial y no se permite el preacondicionamiento de la representación, lo que tiene sentido si el polinomio se evalúa solo una vez. Sin embargo, si se permite el preacondicionamiento y el polinomio se va a evaluar muchas veces, son posibles algoritmos más rápidos . Implican una transformación de la representación del polinomio. En general, un polinomio de grado- n se puede evaluar usando solo ⌊ n / 2 ⌋ +2 multiplicaciones yn adiciones.

Evaluación paralela

Una desventaja de la regla de Horner es que todas las operaciones son secuencialmente dependientes , por lo que no es posible aprovechar el paralelismo del nivel de instrucción en las computadoras modernas. En la mayoría de las aplicaciones donde la eficiencia de la evaluación de polinomios es importante, muchos polinomios de bajo orden se evalúan simultáneamente (para cada píxel o polígono en gráficos por computadora, o para cada cuadrado de la cuadrícula en una simulación numérica), por lo que no es necesario encontrar paralelismo dentro de un evaluación polinomial simple.

Sin embargo, si uno está evaluando un solo polinomio de muy alto orden, puede ser útil dividirlo de la siguiente manera:

${\ Displaystyle {\ begin {alineado} p (x) & = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} \\ & = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n} \\ & = \ left (a_ {0} + a_ {2} x ^ {2} + a_ {4} x ^ {4} + \ cdots \ right) + \ left (a_ {1} x + a_ {3} x ^ {3} + a_ {5} x ^ {5} + \ cdots \ right) \\ & = \ left (a_ {0} + a_ {2} x ^ {2} + a_ {4} x ^ {4} + \ cdots \ right) + x \ left (a_ {1 } + a_ {3} x ^ {2} + a_ {5} x ^ {4} + \ cdots \ right) \\ & = \ sum _ {i = 0} ^ {\ lfloor n / 2 \ rfloor} a_ {2i} x ^ {2i} + x \ sum _ {i = 0} ^ {\ lfloor n / 2 \ rfloor} a_ {2i + 1} x ^ {2i} \\ & = p_ {0} (x ^ {2}) + xp_ {1} (x ^ {2}). \\\ end {alineado}}}$

De manera más general, la suma se puede dividir en k partes:

${\ Displaystyle {\ begin {alineado} p (x) & = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} \\ & = \ sum _ {j = 0} ^ { k-1} x ^ {j} \ sum _ {i = 0} ^ {\ lfloor n / k \ rfloor} a_ {ki + j} x ^ {ki} \\ & = \ sum _ {j = 0} ^ {k-1} x ^ {j} p_ {j} (x ^ {k}) \\\ end {alineado}}}$

donde las sumas internas pueden evaluarse utilizando instancias paralelas separadas del método de Horner. Esto requiere un poco más de operaciones que el método básico de Horner, pero permite la ejecución SIMD de k -way de la mayoría de ellas. Los compiladores modernos generalmente evalúan los polinomios de esta manera cuando es ventajoso, aunque para los cálculos de punto flotante esto requiere habilitar las matemáticas reasociativas (inseguras).

Aplicación a la multiplicación y división en coma flotante

El método de Horner es un método rápido y de código eficiente para la multiplicación y división de números binarios en un microcontrolador sin un multiplicador de hardware . Uno de los números binarios a multiplicar se representa como un polinomio trivial, donde (usando la notación anterior) y . Entonces, x ( ox a alguna potencia) se factoriza repetidamente. En este sistema numérico binario (base 2) , entonces las potencias de 2 se factorizan repetidamente. ${\ Displaystyle a_ {i} = 1}$${\ Displaystyle x = 2}$${\ Displaystyle x = 2}$

Ejemplo

Por ejemplo, para encontrar el producto de dos números (0.15625) ym :

${\ Displaystyle {\ begin {alineado} (0.15625) m & = (0.00101_ {b}) m = (2 ^ {- 3} +2 ^ {- 5}) m = (2 ^ {- 3}) m + ( 2 ^ {- 5}) m \\ & = 2 ^ {- 3} (m + (2 ^ {- 2}) m) = 2 ^ {- 3} (m + 2 ^ {- 2} (m)) . \ end {alineado}}}$

Método

Para encontrar el producto de dos números binarios d y m :

1. Un registro que contiene el resultado intermedio se inicializa en d .

2. Comience con el bit distinto de cero menos significativo (más a la derecha) en m .

2b. Cuente (a la izquierda) el número de posiciones de bit hasta el siguiente bit distinto de cero más significativo. Si no hay bits más significativos, tome el valor de la posición actual del bit.

2c. Usando ese valor, realice una operación de desplazamiento a la izquierda por ese número de bits en el registro que contiene el resultado intermedio

3. Si se contaron todos los bits distintos de cero, entonces el registro de resultado intermedio ahora contiene el resultado final. De lo contrario, agregue d al resultado intermedio y continúe en el paso 2 con el siguiente bit más significativo en m .

Derivación

En general, para un número binario con valores de bits ( ) el producto es ${\ Displaystyle d_ {3} d_ {2} d_ {1} d_ {0}}$

${\ Displaystyle (d_ {3} 2 ^ {3} + d_ {2} 2 ^ {2} + d_ {1} 2 ^ {1} + d_ {0} 2 ^ {0}) m = d_ {3} 2 ^ {3} m + d_ {2} 2 ^ {2} m + d_ {1} 2 ^ {1} m + d_ {0} 2 ^ {0} m.}$

En esta etapa del algoritmo, se requiere que los términos con coeficientes de valor cero se eliminen, de modo que solo se cuenten los coeficientes binarios iguales a uno, por lo que el problema de la multiplicación o división por cero no es un problema, a pesar de esta implicación en el ecuación factorizada:

${\ displaystyle = d_ {0} \ left (m + 2 {\ frac {d_ {1}} {d_ {0}}} \ left (m + 2 {\ frac {d_ {2}} {d_ {1}) }} \ left (m + 2 {\ frac {d_ {3}} {d_ {2}}} (m) \ right) \ right) \ right).}$

Todos los denominadores son iguales (o el término está ausente), por lo que esto se reduce a

${\ Displaystyle = d_ {0} (m + 2 {d_ {1}} (m + 2 {d_ {2}} (m + 2 {d_ {3}} (m)))),}$

o de manera equivalente (de acuerdo con el "método" descrito anteriormente)

${\ Displaystyle = d_ {3} (m + 2 ^ {- 1} {d_ {2}} (m + 2 ^ {- 1} {d_ {1}} (m + {d_ {0}} (m)) )).}$

En matemática binaria (base 2), la multiplicación por una potencia de 2 es simplemente una operación de desplazamiento de registro . Por lo tanto, multiplicar por 2 se calcula en base 2 mediante un desplazamiento aritmético . El factor (2 ⁻¹ ) es un desplazamiento aritmético a la derecha , a (0) no da como resultado ninguna operación (ya que 2 ⁰ = 1 es el elemento de identidad multiplicativo ) y a (2 ¹ ) da como resultado un desplazamiento aritmético a la izquierda. El producto de la multiplicación ahora se puede calcular rápidamente usando solo operaciones aritméticas de desplazamiento, suma y resta.

El método es particularmente rápido en procesadores que admiten un cambio-y-acumulación-suma de una sola instrucción. En comparación con una biblioteca de punto flotante C, el método de Horner sacrifica algo de precisión, sin embargo, es nominalmente 13 veces más rápido (16 veces más rápido cuando se usa el formulario de " dígitos canónicos con signo " (CSD)) y usa solo el 20% del espacio de código.

Otras aplicaciones

El método de Horner puede ser utilizado para convertir entre diferentes posicionales sistemas de numeración - en cuyo caso x es la base del sistema de numeración, y los unos _i coeficientes son los dígitos de la base- x representación de un número dado - y también se puede utilizar si x es una matriz , en cuyo caso la ganancia en eficiencia computacional es aún mayor. Sin embargo, para tales casos se conocen métodos más rápidos .

Hallazgo de raíz polinomial

Usando el algoritmo de división larga en combinación con el método de Newton , es posible aproximar las raíces reales de un polinomio. El algoritmo funciona de la siguiente manera. Dado un polinomio de grado con ceros, haga una suposición inicial tal que . Ahora repita los siguientes dos pasos: ${\ Displaystyle p_ {n} (x)}$${\ Displaystyle n}$${\ Displaystyle z_ {n} <z_ {n-1} <\ cdots <z_ {1},}$${\ Displaystyle x_ {0}}$${\ Displaystyle z_ {1} <x_ {0}}$

1. Usando el método de Newton , encuentre el cero más grande de usar la suposición .${\ Displaystyle z_ {1}}$${\ Displaystyle p_ {n} (x)}$${\ Displaystyle x_ {0}}$
2. Usando el método de Horner, divida para obtener . Regrese al paso 1 pero use el polinomio y la estimación inicial .${\ Displaystyle (x-z_ {1})}$${\ Displaystyle p_ {n-1}}$${\ Displaystyle p_ {n-1}}$${\ Displaystyle z_ {1}}$

Estos dos pasos se repiten hasta que se encuentran todos los ceros reales para el polinomio. Si los ceros aproximados no son lo suficientemente precisos, los valores obtenidos se pueden usar como conjeturas iniciales para el método de Newton, pero usando el polinomio completo en lugar de los polinomios reducidos.

Ejemplo

Considere el polinomio

${\ Displaystyle p_ {6} (x) = (x + 8) (x + 5) (x + 3) (x-2) (x-3) (x-7)}$

que se puede ampliar a

${\ Displaystyle p_ {6} (x) = x ^ {6} + 4x ^ {5} -72x ^ {4} -214x ^ {3} + 1127x ^ {2} + 1602x-5040.}$

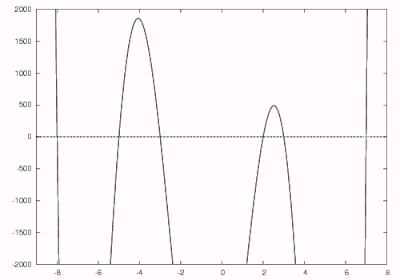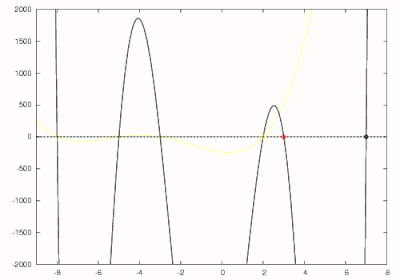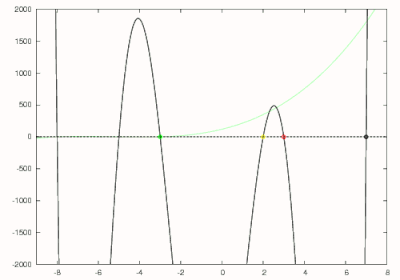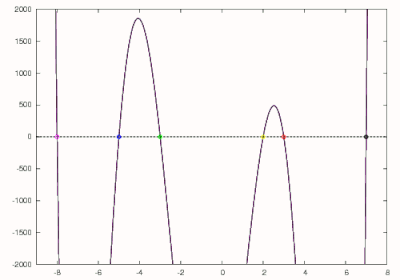
Por lo anterior, sabemos que la raíz más grande de este polinomio es 7, por lo que podemos hacer una estimación inicial de 8. Usando el método de Newton, el primer cero de 7 se encuentra como se muestra en negro en la figura de la derecha. Siguiente se divide por para obtener ${\ Displaystyle p (x)}$${\ Displaystyle (x-7)}$

${\ Displaystyle p_ {5} (x) = x ^ {5} + 11x ^ {4} + 5x ^ {3} -179x ^ {2} -126x + 720}$

que está dibujado en rojo en la figura de la derecha. El método de Newton se usa para encontrar el cero más grande de este polinomio con una estimación inicial de 7. El cero más grande de este polinomio que corresponde al segundo cero más grande del polinomio original se encuentra en 3 y está rodeado en rojo. El polinomio de grado 5 ahora se divide por para obtener ${\ Displaystyle (x-3)}$

${\ Displaystyle p_ {4} (x) = x ^ {4} + 14x ^ {3} + 47x ^ {2} -38x-240}$

que se muestra en amarillo. El cero para este polinomio se encuentra en 2 nuevamente usando el método de Newton y está marcado con un círculo amarillo. El método de Horner ahora se usa para obtener

${\ Displaystyle p_ {3} (x) = x ^ {3} + 16x ^ {2} + 79x + 120}$

que se muestra en verde y tiene un cero en −3. Este polinomio se reduce aún más a

${\ Displaystyle p_ {2} (x) = x ^ {2} + 13x + 40}$

que se muestra en azul y produce un cero de -5. La raíz final del polinomio original se puede encontrar usando el cero final como una suposición inicial para el método de Newton o reduciendo y resolviendo la ecuación lineal. Como puede verse, se encontraron las raíces esperadas de −8, −5, −3, 2, 3 y 7. ${\ Displaystyle p_ {2} (x)}$

Diferencia dividida de un polinomio

El método de Horner se puede modificar para calcular la diferencia dividida Dado el polinomio (como antes) ${\ Displaystyle (p (y) -p (x)) / (yx).}$

${\ Displaystyle p (x) = \ sum _ {i = 0} ^ {n} a_ {i} x ^ {i} = a_ {0} + a_ {1} x + a_ {2} x ^ {2} + a_ {3} x ^ {3} + \ cdots + a_ {n} x ^ {n},}$

proceder de la siguiente

${\ Displaystyle {\ begin {alineado} b_ {n} & = a_ {n}, & \ quad d_ {n} & = b_ {n}, \\ b_ {n-1} & = a_ {n-1} + b_ {n} x, & \ quad d_ {n-1} & = b_ {n-1} + d_ {n} y, \\ & {} \ \ \ vdots & \ quad & {} \ \ \ vdots \\ b_ {1} & = a_ {1} + b_ {2} x, & \ quad d_ {1} & = b_ {1} + d_ {2} y, \\ b_ {0} & = a_ {0 } + b_ {1} x. \ end {alineado}}}$

Al finalizar, tenemos

${\ Displaystyle {\ begin {alineado} p (x) & = b_ {0}, \\ {\ frac {p (y) -p (x)} {yx}} & = d_ {1}, \\ p (y) & = b_ {0} + (yx) d_ {1}. \ end {alineado}}}$

Este cálculo de la diferencia dividida está sujeto a menos errores de redondeo que la evaluación y por separado, particularmente cuando . Sustituyendo en este método , se obtiene la derivada de . ${\ Displaystyle p (x)}$${\ Displaystyle p (y)}$${\ Displaystyle x \ approx y}$${\ Displaystyle y = x}$${\ Displaystyle d_ {1} = p '(x)}$${\ Displaystyle p (x)}$

Historia

El artículo de Horner, titulado "Un nuevo método para resolver ecuaciones numéricas de todos los órdenes, por aproximación continua", se leyó ante la Royal Society de Londres, en su reunión del 1 de julio de 1819, con una secuela en 1823. El artículo de Horner en la Parte II de Philosophical Transactions de la Royal Society de Londres de 1819 fue acogido cálida y ampliamente por un crítico en el número de The Monthly Review: o, Literary Journal de abril de 1820; en comparación, un artículo técnico de Charles Babbage se descarta tajantemente en esta revisión. La secuencia de revisiones en The Monthly Review de septiembre de 1821 concluye que Holdred fue la primera persona en descubrir una solución práctica directa y general de ecuaciones numéricas. Fuller mostró que el método en el artículo de Horner de 1819 difiere de lo que luego se conoció como "método de Horner" y que, en consecuencia, la prioridad para este método debería ir a Holdred (1820).

A diferencia de sus contemporáneos ingleses, Horner se basó en la literatura continental, especialmente en la obra de Arbogast . También se sabe que Horner hizo una lectura atenta del libro de álgebra de John Bonneycastle, aunque descuidó el trabajo de Paolo Ruffini .

Aunque a Horner se le atribuye el mérito de hacer accesible y práctico el método, se conocía mucho antes que Horner. En orden cronológico inverso, el método de Horner ya era conocido por:

• Paolo Ruffini en 1809 (ver la regla de Ruffini )
• Isaac Newton en 1669
• el matemático chino Zhu Shijie en el siglo XIV
• el matemático chino Qin Jiushao en su Tratado matemático en nueve secciones en el siglo XIII
• el matemático persa Sharaf al-Dīn al-Ṭūsī en el siglo XII (el primero en usar ese método en un caso general de ecuación cúbica)
• el matemático chino Jia Xian en el siglo XI ( dinastía Song )
• Los nueve capítulos sobre el arte matemático , una obra china de la dinastía Han (202 a. C. - 220 d. C.) editada por Liu Hui (fl. Siglo III).

Qin Jiushao , en su Shu Shu Jiu Zhang ( Tratado matemático en nueve secciones ; 1247), presenta una carpeta de métodos de tipo Horner para resolver ecuaciones polinomiales, que se basó en trabajos anteriores del matemático de la dinastía Song del siglo XI, Jia Xian ; por ejemplo, un método se adapta específicamente a los bi-quínticos, del cual Qin da un ejemplo, de acuerdo con la costumbre china de entonces de los estudios de casos. Yoshio Mikami en Desarrollo de las matemáticas en China y Japón (Leipzig 1913) escribió:

"... quién puede negar el hecho de que el ilustre proceso de Horner se haya utilizado en China al menos casi seis largos siglos antes que en Europa ... Por supuesto, no pretendemos de ninguna manera atribuir la invención de Horner a un origen chino, pero el paso del tiempo hace que no sea del todo imposible que los europeos pudieran haber conocido el método chino de forma directa o indirecta ".

Ulrich Libbrecht concluyó: Es obvio que este procedimiento es una invención china ... el método no se conocía en la India . Dijo que Fibonacci probablemente se enteró de ello por los árabes, que quizás lo tomaron prestado de los chinos. La extracción de raíces cuadradas y cúbicas a lo largo de líneas similares ya la analiza Liu Hui en relación con los problemas IV.16 y 22 en Jiu Zhang Suan Shu , mientras que Wang Xiaotong en el siglo VII supone que sus lectores pueden resolver cúbicos mediante un método de aproximación descrito en su libro Jigu Suanjing .

Ver también

• Algoritmo de Clenshaw para evaluar polinomios en forma de Chebyshev
• El algoritmo de de Boor para evaluar las estrías en B-spline forma
• Algoritmo de de Casteljau para evaluar polinomios en forma Bézier
• Esquema de Estrin para facilitar la paralelización en arquitecturas informáticas modernas
• El método de Lill para aproximar raíces gráficamente
• Regla de Ruffini y división sintética para dividir un polinomio por un binomio de la forma x - r

Notas

Referencias

• Berggren, JL (1990). "Innovación y tradición en Muadalat de Sharaf al-Din al-Tusi". Revista de la Sociedad Oriental Americana . 110 (2): 304-309. doi : 10.2307 / 604533 . JSTOR  604533 .
• Cajori, Florian (1911). "Método de aproximación de Horner anticipado por Ruffini" . Boletín de la American Mathematical Society . 17 (8): 409–414. doi : 10.1090 / s0002-9904-1911-02072-9 . Lea ante la Sección Suroeste de la American Mathematical Society el 26 de noviembre de 1910.
• Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein 10.1016 / 0315-0860 (81) 90069-0, Clifford (2009). "Introducción a los algoritmos" . Historia Mathematica (3ª ed.). MIT Press. 8 (3): 277–318. doi : 10.1016 / 0315-0860 (81) 90069-0 .
• Fateman, RJ ; Kahan, W. (2000). Mejora de integrales exactas de sistemas de álgebra simbólica (PDF) (Informe). PAM. Universidad de California, Berkeley: Centro de Matemáticas Puras y Aplicadas. Archivado desde el original (PDF) el 14 de agosto de 2017 . Consultado el 17 de mayo de 2018 .
• Fuller, AT (1999). "Horner versus Holdred: un episodio en la historia de la computación raíz" . Historia Mathematica . 26 : 29–51. doi : 10.1006 / hmat.1998.2214 .
• Higham, Nicholas (2002). Precisión y estabilidad de algoritmos numéricos . SIAM. ISBN 978-0-89871-521-7.
• Holdred, T. (1820). Un nuevo método para resolver ecuaciones con facilidad y rapidez; por el cual se encuentra el valor verdadero de la cantidad desconocida sin reducción previa. Con un suplemento, que contiene otros dos métodos para resolver ecuaciones, derivados del mismo principio (PDF) . Richard Watts. Archivado desde el original (PDF) el 6 de enero de 2014 . Consultado el 10 de diciembre de 2012 .

  El método de Holdred se encuentra en el suplemento que sigue a la página 45 (que es la página 52 de la versión en pdf).

• Horner, William George (julio de 1819). "Un nuevo método de resolución de ecuaciones numéricas de todos los órdenes, por aproximación continua" (PDF) . Transacciones filosóficas . Royal Society de Londres. 109 : 308–335. doi : 10.1098 / rstl.1819.0023 . JSTOR  107508 . S2CID  186210512 . Archivado desde el original (PDF) el 28 de marzo de 2017 . Consultado el 28 de marzo de 2017 .

  Disponible directamente en línea a través del enlace, pero también reimpreso con evaluación en DE Smith: A Source Book in Mathematics , McGraw-Hill, 1929; Reimpresión de Dover, 2 vols, 1959.

• Knuth, Donald (1997). El arte de la programación informática . Vol. 2: Algoritmos seminuméricos (3ª ed.). Addison-Wesley. págs. 486–488 en la sección 4.6.4. ISBN 978-0-201-89684-8. |volume=tiene texto extra ( ayuda )
• Kress, Rainer (1991). Análisis numérico . Saltador.
• Kripasagar, Venkat (marzo de 2008). "Micro matemáticas eficientes - técnicas de multiplicación y división para MCU". Revista Circuit Cellar (212).
• Libbrecht, Ulrich (2005). "Capítulo 13" . Matemáticas chinas en el siglo XIII (2ª ed.). Dover. ISBN 978-0-486-44619-6. Archivado desde el original el 6 de junio de 2017 . Consultado el 23 de agosto de 2016 .
• Mikami, Yoshio (1913). "Capítulo 11. Ch'in Chiu-Shao" . El desarrollo de las matemáticas en China y Japón (1ª ed.). Reimpresión de Chelsea Publishing Co. págs. 74–77.
• Ostrowski, Alexander M. (1954). "Sobre dos problemas de álgebra abstracta relacionados con la regla de Horner" . Estudios en Matemática y Mecánica presentados a Richard von Mises . Prensa académica. págs. 40–48. ISBN 978-1-4832-3272-0.
• Pan, Y. Ja (1966). "Sobre medios para calcular valores de polinomios". Matemáticas rusas. Encuestas . 21 : 105-136. doi : 10.1070 / rm1966v021n01abeh004147 .
• Pankiewicz, W. (1968). "Algoritmo 337: cálculo de un polinomio y sus valores derivados por esquema de Horner". Comunicaciones de la ACM . ACM. 11 (9): 633. doi : 10.1145 / 364063.364089 . S2CID  52859619 .
• Spiegel, Murray R. (1956). Esquema de la teoría y problemas del álgebra universitaria de Schaum . McGraw-Hill.
• Temple, Robert (1986). El genio de China: 3.000 años de ciencia, descubrimiento e invención . Simon y Schuster. ISBN 978-0-671-62028-8.
• Whittaker, ET ; Robinson, G. (1924). El cálculo de las observaciones . Londres: Blackie.
• Wylie, Alexander (1897). "Apuntes sobre la ciencia de la aritmética china" . Investigaciones chinas . Llevar a la fuerza. págs. 159-194.

  Reimpreso de números de The North China Herald (1852).

enlaces externos

• "Esquema de Horner" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Qiu Jin-Shao, Shu Shu Jiu Zhang (Cong Shu Ji Cheng ed.)
• Para obtener más información sobre la aplicación de búsqueda de raíces, consulte [1]