Sistema de Hilbert - Hilbert system

En física matemática , el sistema de Hilbert es un término que se usa con poca frecuencia para un sistema físico descrito por un C * -álgebra .

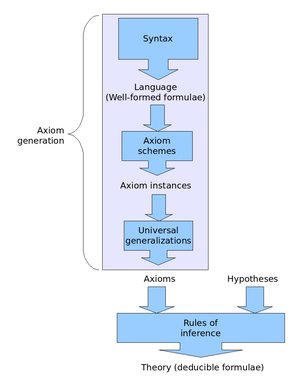
En lógica , especialmente lógica matemática , un sistema de Hilbert , a veces llamado cálculo de Hilbert , sistema deductivo al estilo de Hilbert o sistema de Hilbert-Ackermann , es un tipo de sistema de deducción formal atribuido a Gottlob Frege y David Hilbert . Estos sistemas deductivos se estudian con mayor frecuencia para la lógica de primer orden , pero también son de interés para otras lógicas.

La mayoría de las variantes de sistemas de Hilbert toman un rumbo característico en la forma en que equilibran un equilibrio entre los axiomas lógicos y reglas de inferencia . Los sistemas de Hilbert pueden caracterizarse por la elección de un gran número de esquemas de axiomas lógicos y un pequeño conjunto de reglas de inferencia . Los sistemas de deducción natural toman el rumbo opuesto, incluidas muchas reglas de deducción pero muy pocos o ningún esquema de axiomas. Los sistemas de Hilbert más comúnmente estudiados tienen una sola regla de inferencia, modus ponens , para la lógica proposicional  , o dos, con generalización , para manejar también la lógica de predicados , y varios esquemas de axiomas infinitos. Los sistemas de Hilbert para lógicas modales proposicionales , a veces llamados sistemas de Hilbert-Lewis , generalmente se axiomatizan con dos reglas adicionales, la regla de necesidad y la regla de sustitución uniforme .

Un rasgo característico de las muchas variantes de los sistemas de Hilbert es que el contexto no cambia en ninguna de sus reglas de inferencia, mientras que tanto la deducción natural como el cálculo secuencial contienen algunas reglas de cambio de contexto. Por lo tanto, si uno está interesado solo en la derivabilidad de tautologías , no en juicios hipotéticos, entonces uno puede formalizar el sistema de Hilbert de tal manera que sus reglas de inferencia contengan solo juicios de una forma bastante simple. No se puede hacer lo mismo con los otros dos sistemas de deducciones: como se cambia el contexto en algunas de sus reglas de inferencia, no se pueden formalizar para evitar juicios hipotéticos, ni siquiera si queremos usarlos solo para probar la derivabilidad de tautologías. .

Deducciones formales

En un sistema de deducción al estilo de Hilbert, una deducción formal es una secuencia finita de fórmulas en la que cada fórmula es un axioma o se obtiene de fórmulas anteriores mediante una regla de inferencia. Estas deducciones formales están destinadas a reflejar las pruebas en lenguaje natural, aunque son mucho más detalladas.

Supongamos que es un conjunto de fórmulas, consideradas como hipótesis . Por ejemplo, podría ser un conjunto de axiomas para la teoría de grupos o la teoría de conjuntos . La notación significa que hay una deducción que termina usando como axiomas solo axiomas lógicos y elementos de . Por lo tanto, informalmente, significa que es demostrable asumiendo todas las fórmulas en . ${\ Displaystyle \ Gamma}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ Gamma \ vdash \ phi}$${\ Displaystyle \ phi}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ Gamma \ vdash \ phi}$${\ Displaystyle \ phi}$${\ Displaystyle \ Gamma}$

Los sistemas de deducción al estilo de Hilbert se caracterizan por el uso de numerosos esquemas de axiomas lógicos . Un esquema de axiomas es un conjunto infinito de axiomas que se obtienen al sustituir todas las fórmulas de alguna forma en un patrón específico. El conjunto de axiomas lógicos incluye no solo los axiomas generados a partir de este patrón, sino también cualquier generalización de uno de esos axiomas. Se obtiene una generalización de una fórmula prefijando cero o más cuantificadores universales en la fórmula; por ejemplo, es una generalización de . ${\ Displaystyle \ forall y (\ forall xPxy \ to Pty)}$${\ Displaystyle \ forall xPxy \ to Pty}$

Axiomas lógicos

Hay varias axiomatizaciones variantes de la lógica de predicados, ya que para cualquier lógica hay libertad para elegir axiomas y reglas que caracterizan esa lógica. Aquí describimos un sistema de Hilbert con nueve axiomas y solo la regla modus ponens, que llamamos axiomatización de una regla y que describe la lógica ecuacional clásica. Nos ocupamos de un lenguaje mínimo para esta lógica, donde las fórmulas utilizan sólo los conectivos y ya sólo el cuantificador . Más adelante mostramos cómo se puede ampliar el sistema para incluir conectivos lógicos adicionales, como y , sin ampliar la clase de fórmulas deducibles. ${\ Displaystyle \ lnot}$${\ Displaystyle \ to}$${\ Displaystyle \ forall}$${\ Displaystyle \ land}$${\ Displaystyle \ lor}$

Los primeros cuatro esquemas de axiomas lógicos permiten (junto con modus ponens) la manipulación de conectivos lógicos.

P1. ${\ Displaystyle \ phi \ to \ phi}$

P2. ${\ Displaystyle \ phi \ to \ left (\ psi \ to \ phi \ right)}$

P3. ${\ Displaystyle \ left (\ phi \ to \ left (\ psi \ rightarrow \ xi \ right) \ right) \ to \ left (\ left (\ phi \ to \ psi \ right) \ to \ left (\ phi \ a \ xi \ derecha) \ derecha)}$

P4. ${\ Displaystyle \ left (\ lnot \ phi \ to \ lnot \ psi \ right) \ to \ left (\ psi \ to \ phi \ right)}$

El axioma P1 es redundante, como se desprende de P3, P2 y modus ponens (ver prueba ). Estos axiomas describen la lógica proposicional clásica ; sin el axioma P4 obtenemos lógica implicacional positiva . La lógica mínima se logra agregando en su lugar el axioma P4m o definiendo como . ${\ Displaystyle \ lnot \ phi}$${\ Displaystyle \ phi \ to \ bot}$

P4m. ${\ Displaystyle \ left (\ phi \ to \ psi \ right) \ to \ left (\ left (\ phi \ to \ lnot \ psi \ right) \ to \ lnot \ phi \ right)}$

La lógica intuicionista se logra agregando los axiomas P4i y P5i a la lógica implicacional positiva, o agregando el axioma P5i a la lógica mínima. Tanto P4i como P5i son teoremas de la lógica proposicional clásica.

P4i. ${\ Displaystyle \ left (\ phi \ to \ lnot \ phi \ right) \ to \ lnot \ phi}$

P5i. ${\ Displaystyle \ lnot \ phi \ to \ left (\ phi \ to \ psi \ right)}$

Tenga en cuenta que estos son esquemas de axiomas, que representan un número infinito de casos específicos de axiomas. Por ejemplo, P1 podría representar la instancia de axioma particular , o podría representar : es un lugar donde se puede colocar cualquier fórmula. Una variable como ésta que se extiende sobre las fórmulas se denomina 'variable esquemática'. ${\ Displaystyle p \ to p}$${\ Displaystyle \ left (p \ to q \ right) \ to \ left (p \ to q \ right)}$${\ Displaystyle \ phi}$

Con una segunda regla de sustitución uniforme (EE. UU.), Podemos cambiar cada uno de estos esquemas de axioma en un solo axioma, reemplazando cada variable esquemática por alguna variable proposicional que no se menciona en ningún axioma para obtener lo que llamamos la axiomatización sustitucional. Ambas formalizaciones tienen variables, pero donde la axiomatización de una regla tiene variables esquemáticas que están fuera del lenguaje de la lógica, la axiomatización sustitutiva usa variables proposicionales que hacen el mismo trabajo al expresar la idea de una variable que va sobre fórmulas con una regla que usa sustitución.

NOSOTROS. Sea una fórmula con una o más instancias de la variable proposicional y sea ​​otra fórmula. Luego de , inferir .${\ Displaystyle \ phi (p)}$${\ Displaystyle p}$${\ Displaystyle \ psi}$${\ Displaystyle \ phi (p)}$${\ Displaystyle \ phi (\ psi)}$

Los siguientes tres esquemas de axiomas lógicos proporcionan formas de agregar, manipular y eliminar cuantificadores universales.

Q5. donde t puede ser sustituido por x en${\ Displaystyle \ forall x \ left (\ phi \ right) \ to \ phi [x: = t]}$${\ Displaystyle \, \! \ phi}$

Q6. ${\ Displaystyle \ forall x \ left (\ phi \ to \ psi \ right) \ to \ left (\ forall x \ left (\ phi \ right) \ to \ forall x \ left (\ psi \ right) \ right) }$

Q7. donde x no está libre en .${\ Displaystyle \ phi \ to \ forall x \ left (\ phi \ right)}$${\ Displaystyle \ phi}$

Estas tres reglas adicionales amplían el sistema proposicional para axiomatizar la lógica de predicados clásica . Asimismo, estas tres reglas extienden el sistema de la lógica proposicional intuicionista (con P1-3 y P4i y P5i) a la lógica de predicados intuicionista .

A la cuantificación universal a menudo se le da una axiomatización alternativa usando una regla adicional de generalización (ver la sección sobre Metateoremas), en cuyo caso las reglas Q6 y Q7 son redundantes.

Se requiere que los esquemas de axiomas finales trabajen con fórmulas que involucren el símbolo de igualdad.

I8. para cada variable x .${\ Displaystyle x = x}$

I9. ${\ Displaystyle \ left (x = y \ right) \ to \ left (\ phi [z: = x] \ to \ phi [z: = y] \ right)}$

Extensiones conservadoras

Es común incluir en un sistema de deducción al estilo de Hilbert solo axiomas para la implicación y la negación. Dados estos axiomas, es posible formar extensiones conservadoras del teorema de deducción que permitan el uso de conectivos adicionales. Estas extensiones se denominan conservativas porque si una fórmula φ que involucra nuevas conectivas se reescribe como una fórmula lógicamente equivalente θ que involucra solo negación, implicación y cuantificación universal, entonces φ es derivable en el sistema extendido si y solo si θ es derivable en el sistema original . Cuando está completamente extendido, un sistema al estilo de Hilbert se parecerá más a un sistema de deducción natural .

Cuantificación existencial

• Introducción

${\ Displaystyle \ forall x (\ phi \ to \ existe y (\ phi [x: = y]))}$

• Eliminación

${\ Displaystyle \ forall x (\ phi \ a \ psi) \ a \ existe x (\ phi) \ a \ psi}$donde no es una variable libre de .${\ Displaystyle x}$${\ Displaystyle \ psi}$

Conjunción y disyunción

• Introducción y eliminación de conjunciones

Introducción: ${\ Displaystyle \ alpha \ to \ beta \ to \ alpha \ land \ beta}$

eliminación izquierda: ${\ Displaystyle \ alpha \ wedge \ beta \ to \ alpha}$

derecho de eliminación: ${\ Displaystyle \ alpha \ wedge \ beta \ to \ beta}$

• Introducción y eliminación de disyunciones

introducción a la izquierda: ${\ Displaystyle \ alpha \ to \ alpha \ vee \ beta}$

introducción derecha: ${\ Displaystyle \ beta \ to \ alpha \ vee \ beta}$

eliminación: ${\ Displaystyle (\ alpha \ to \ gamma) \ to (\ beta \ to \ gamma) \ to \ alpha \ vee \ beta \ to \ gamma}$

Metateoremas

Debido a que los sistemas estilo Hilbert tienen muy pocas reglas de deducción, es común probar metateoremas que muestran que las reglas de deducción adicionales no agregan poder deductivo, en el sentido de que una deducción que usa las nuevas reglas de deducción se puede convertir en una deducción usando solo la deducción original. normas.

Algunos metateoremas comunes de esta forma son:

• El teorema de la deducción : si y solo si .${\ Displaystyle \ Gamma; \ phi \ vdash \ psi}$${\ Displaystyle \ Gamma \ vdash \ phi \ to \ psi}$
• ${\ Displaystyle \ Gamma \ vdash \ phi \ leftrightarrow \ psi}$si y solo si y .${\ Displaystyle \ Gamma \ vdash \ phi \ to \ psi}$${\ Displaystyle \ Gamma \ vdash \ psi \ to \ phi}$
• Contraposición: Si entonces .${\ Displaystyle \ Gamma; \ phi \ vdash \ psi}$${\ Displaystyle \ Gamma; \ lnot \ psi \ vdash \ lnot \ phi}$
• Generalización : Si y x no ocurre libre en cualquier fórmula de continuación .${\ Displaystyle \ Gamma \ vdash \ phi}$${\ Displaystyle \ Gamma}$${\ Displaystyle \ Gamma \ vdash \ forall x \ phi}$

Algunos teoremas útiles y sus demostraciones

A continuación se presentan varios teoremas en lógica proposicional, junto con sus demostraciones (o enlaces a estas demostraciones en otros artículos). Tenga en cuenta que, dado que (P1) en sí mismo se puede demostrar utilizando los otros axiomas, de hecho (P2), (P3) y (P4) son suficientes para demostrar todos estos teoremas.

(HS1) - Silogismo hipotético , ver prueba .${\ Displaystyle (q \ to r) \ to ((p \ to q) \ to (p \ to r))}$

(L1) - prueba: ${\ Displaystyle p \ a ((p \ a q) \ a q)}$

(1)       (instancia de (P3))${\ Displaystyle ((p \ a q) \ a (p \ a q)) \ a (((p \ a q) \ a p) \ a ((p \ a q) \ a q))}$

(2)       (instancia de (P1))${\ Displaystyle (p \ to q) \ to (p \ to q)}$

(3)       (de (2) y (1) por modus ponens )${\ Displaystyle ((p \ to q) \ to p) \ to ((p \ to q) \ to q)}$

(4)       (instancia de (HS1))${\ Displaystyle (((p \ to q) \ to p) \ to ((p \ to q) \ to q)) \ to ((p \ to ((p \ to q) \ to p)) \ to (p \ a ((p \ a q) \ a q)))}$

(5)       (de (3) y (4) por modus ponens)${\ Displaystyle (p \ to ((p \ to q) \ to p)) \ to (p \ to ((p \ to q) \ to q))}$

(6)       (instancia de (P2))${\ Displaystyle p \ a ((p \ a q) \ a p)}$

(7)       (de (6) y (5) por modus ponens)${\ Displaystyle p \ a ((p \ a q) \ a q)}$

Los siguientes dos teoremas se conocen juntos como doble negación :

(DN1)${\ Displaystyle \ neg \ neg p \ to p}$

(DN2) ${\ Displaystyle p \ to \ neg \ neg p}$

Ver pruebas .

(L2) - para esta prueba usamos el método del metateorema del silogismo hipotético como una forma abreviada de varios pasos de prueba: ${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to r))}$

(1)       (instancia de (P3))${\ Displaystyle (p \ to (q \ to r)) \ to ((p \ to q) \ to (p \ to r))}$

(2)       (instancia de (HS1))${\ Displaystyle ((p \ to q) \ to (p \ to r)) \ to ((q \ to (p \ to q)) \ to (q \ to (p \ to r)))}$

(3)       (de (1) y (2) usando el metateorema del silogismo hipotético)${\ Displaystyle (p \ a (q \ a r)) \ a ((q \ a (p \ a q)) \ a (q \ a (p \ a r)))}$

(4)       (instancia de (P3))${\ Displaystyle ((p \ to (q \ to r)) \ to ((q \ to (p \ to q)) \ to (q \ to (p \ to r)))) \ to (((p \ a (q \ a r)) \ a (q \ a (p \ a q))) \ a ((p \ a (q \ a r)) \ a (q \ a (p \ a r)) ))}$

(5)       (de (3) y (4) usando modus ponens)${\ Displaystyle ((p \ to (q \ to r)) \ to (q \ to (p \ to q))) \ to ((p \ to (q \ to r)) \ to (q \ to ( p \ a r)))}$

(6)       (instancia de (P2))${\ Displaystyle q \ to (p \ to q)}$

(7)       (instancia de (P2))${\ Displaystyle (q \ to (p \ to q)) \ to ((p \ to (q \ to r)) \ to (q \ to (p \ to q)))}$

(8)       (de (6) y (7) usando modus ponens)${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to q))}$

(9)       (de (8) y (5) usando modus ponens)${\ Displaystyle (p \ to (q \ to r)) \ to (q \ to (p \ to r))}$

(HS2) - una forma alternativa del silogismo hipotético . prueba: ${\ Displaystyle (p \ to q) \ to ((q \ to r) \ to (p \ to r))}$

(1)       (instancia de (HS1))${\ Displaystyle (q \ to r) \ to ((p \ to q) \ to (p \ to r))}$

(2)       (instancia de (L2))${\ Displaystyle ((q \ to r) \ to ((p \ to q) \ to (p \ to r))) \ to ((p \ to q) \ to ((q \ to r) \ to ( p \ a r)))}$

(3) (de (1) y (2) por modus ponens)${\ Displaystyle (p \ to q) \ to ((q \ to r) \ to (p \ to r))}$

(TR1) - Transposición, ver prueba (la otra dirección de transposición es (P4)).${\ Displaystyle (p \ to q) \ to (\ neg q \ to \ neg p)}$

(TR2) - otra forma de transposición; prueba: ${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to p)}$

(1)       (instancia de (TR1))${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to \ neg \ neg p)}$

(2)       (instancia de (DN1))${\ Displaystyle \ neg \ neg p \ to p}$

(3)       (instancia de (HS1))${\ Displaystyle (\ neg \ neg p \ ap) \ to ((\ neg q \ to \ neg \ neg p) \ to (\ neg q \ ap))}$

(4)       (de (2) y (3) por modus ponens)${\ Displaystyle (\ neg q \ to \ neg \ neg p) \ to (\ neg q \ to p)}$

(5)       (de (1) y (4) usando el metateorema del silogismo hipotético)${\ Displaystyle (\ neg p \ to q) \ to (\ neg q \ to p)}$

(L3) - prueba: ${\ Displaystyle (\ neg p \ ap) \ ap}$

(1)       (instancia de (P2))${\ Displaystyle \ neg p \ to (\ neg \ neg (q \ to q) \ to \ neg p)}$

(2)       (instancia de (P4))${\ Displaystyle (\ neg \ neg (q \ to q) \ to \ neg p) \ to (p \ to \ neg (q \ to q))}$

(3)       (de (1) y (2) usando el metateorema del silogismo hipotético)${\ Displaystyle \ neg p \ to (p \ to \ neg (q \ to q))}$

(4)       (instancia de (P3))${\ Displaystyle (\ neg p \ to (p \ to \ neg (q \ to q))) \ to ((\ neg p \ to p) \ to (\ neg p \ to \ neg (q \ to q) ))}$

(5)       (de (3) y (4) usando modos ponens)${\ Displaystyle (\ neg p \ ap) \ to (\ neg p \ to \ neg (q \ to q))}$

(6)       (instancia de (P4))${\ Displaystyle (\ neg p \ to \ neg (q \ to q)) \ to ((q \ to q) \ to p)}$

(7)       (de (5) y (6) usando el metateorema del silogismo hipotético)${\ Displaystyle (\ neg p \ to p) \ to ((q \ to q) \ to p)}$

(8)       (instancia de (P1))${\ Displaystyle q \ to q}$

(9)       (instancia de (L1))${\ Displaystyle (q \ to q) \ to (((q \ to q) \ to p) \ to p)}$

(10)       (de (8) y (9) usando modos ponens)${\ Displaystyle ((q \ to q) \ to p) \ to p}$

(11)       (de (7) y (10) utilizando el metateorema del silogismo hipotético)${\ Displaystyle (\ neg p \ ap) \ ap}$

Axiomatizaciones alternativas

El axioma 3 anterior se le atribuye a Łukasiewicz . El sistema original de Frege tenía los axiomas P2 y P3, pero otros cuatro axiomas en lugar del axioma P4 (véase el cálculo proposicional de Frege ). Russell y Whitehead también sugirieron un sistema con cinco axiomas proposicionales.

Otras conexiones

Los axiomas P1, P2 y P3, con la regla de deducción modus ponens (que formaliza la lógica proposicional intuicionista ), corresponden a los combinadores de base lógica combinatoria I , K y S con el operador de aplicación. Las demostraciones en el sistema de Hilbert corresponden a los términos combinatorios en lógica combinatoria. Véase también la correspondencia de Curry-Howard .

Ver también

• Lista de sistemas Hilbert
• Deducción natural

Notas

Referencias

• Curry, Haskell B .; Robert Feys (1958). Lógica combinatoria Vol. Yo . 1 . Amsterdam: Holanda Septentrional.
• Monk, J. Donald (1976). Lógica matemática . Textos de Posgrado en Matemáticas. Berlín, Nueva York: Springer-Verlag . ISBN 978-0-387-90170-1.CS1 maint: posdata ( enlace )
• Ruzsa, Imre; Máté, András (1997). Bevezetés a modern logikába (en húngaro). Budapest: Osiris Kiadó.
• Tarski, Alfred (1990). Bizonyítás és igazság (en húngaro). Budapest: telecabina.Es una traducción al húngaro de los artículos seleccionados de Alfred Tarski sobre la teoría semántica de la verdad .
• David Hilbert (1927) "Los fundamentos de las matemáticas", traducido por Stephan Bauer-Menglerberg y Dagfinn Føllesdal (págs. 464–479). en:
  • van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931 (tercera edición, 1976 ed.). Cambridge MA: Harvard University Press. ISBN 0-674-32449-8.
  • Hilbert de 1927, basado en una conferencia anterior de 1925 sobre "fundamentos" (págs. 367-392), presenta sus 17 axiomas: axiomas de implicación # 1-4, axiomas sobre & y V # 5-10, axiomas de negación # 11- 12, su ε-axioma lógico n. ° 13, axiomas de igualdad n. ° 14-15 y axiomas del número n. ° 16-17, junto con los otros elementos necesarios de su "teoría de la prueba" formalista, por ejemplo, axiomas de inducción, axiomas de recursividad, etc; también ofrece una enérgica defensa contra el intuicionismo de LEJ Brouwer. Véanse también los comentarios y la refutación de Hermann Weyl (1927) (págs. 480-484), el apéndice de Paul Bernay (1927) a la conferencia de Hilbert (págs. 485-489) y la respuesta de Luitzen Egbertus Jan Brouwer (1927) (págs. 490-495)
• Kleene, Stephen Cole (1952). Introducción a las metamatemáticas (décima impresión con corrección de 1971 ed.). Amsterdam NY: North Holland Publishing Company. ISBN 0-7204-2103-9.
  • Ver en particular el Capítulo IV Sistema formal (págs. 69-85) donde Kleene presenta subcapítulos §16 Símbolos formales, §17 Reglas de formación, §18 Variables libres y ligadas (incluida la sustitución), §19 Reglas de transformación (por ejemplo, modus ponens) - y de éstos presenta 21 "postulados" - 18 axiomas y 3 relaciones de "consecuencia inmediata" divididas de la siguiente manera: Postulados para el cálculo proposicional # 1-8, Postulados adicionales para el cálculo de predicados # 9-12, y Postulados adicionales para teoría de números # 13-21.

enlaces externos

• Gaifman, Haim. "Un sistema deductivo de tipo Hilbert para la lógica de las oraciones, la integridad y la compacidad" (pdf) .
• Farmer, WM "Lógica proposicional" (pdf) .Describe (entre otros) una parte del sistema de deducción al estilo de Hilbert (restringido al cálculo proposicional ).