Curva de Bézier compuesta -Composite Bézier curve

Beziergon: el beziergon rojo pasa a través de los vértices azules, los puntos verdes son puntos de control que determinan la forma de las curvas de Bézier que se conectan

En el modelado geométrico y en gráficos por computadora , una curva de Bézier compuesta o spline de Bézier es una spline hecha de curvas de Bézier que es al menos continua . En otras palabras, una curva de Bézier compuesta es una serie de curvas de Bézier unidas de extremo a extremo donde el último punto de una curva coincide con el punto inicial de la siguiente curva. Dependiendo de la aplicación, se pueden agregar requisitos adicionales de suavidad (como o continuidad). ${\ estilo de visualización C^{0}}$ ${\ estilo de visualización C^{1}}$${\ estilo de visualización C^{2}}$

Un Bézier compuesto continuo también se denomina polibezier , por similitud con polilínea , pero mientras que en las polilíneas los puntos están conectados por líneas rectas, en un polibezier los puntos están conectados por curvas de Bézier. Un beziergon (también llamado bezigon ) es un camino cerrado compuesto por curvas de Bézier . Es similar a un polígono en que conecta un conjunto de vértices por líneas, pero mientras que en los polígonos los vértices están conectados por líneas rectas, en un beziergon los vértices están conectados por curvas de Bézier. Algunos autores incluso llaman a una curva de Bézier compuesta "spline de Bézier"; Sin embargo, otros autores utilizan este último término como sinónimo de la curva de Bézier (no compuesta), y agregan "compuesto" delante de "Bézier spline" para indicar el caso compuesto. ${\ estilo de visualización C^{0}}$

Quizás el uso más común de los Béziers compuestos es describir el contorno de cada letra en un archivo PostScript o PDF . Dichos contornos se componen de un beziergon para letras abiertas o varios beziergon para letras cerradas. Los gráficos vectoriales modernos y los sistemas de fuentes informáticas como PostScript , Asymptote , Metafont , OpenType y SVG utilizan curvas Bézier compuestas compuestas por curvas Bézier cúbicas (curvas de tercer orden) para dibujar formas curvas.

Función sinc aproximada utilizando una spline Bézier suave, es decir, una serie de curvas Bézier unidas suavemente

Unión suave

Una propiedad comúnmente deseada de las splines es que unan sus curvas individuales con un nivel específico de continuidad paramétrica o geométrica . Si bien las curvas individuales en la spline son completamente continuas dentro de su propio intervalo, siempre hay cierta cantidad de discontinuidad donde se encuentran diferentes curvas. ${\displaystyle C^{\infty}}$

La spline de Bézier es bastante única en el sentido de que es una de las pocas splines que no garantiza un mayor grado de continuidad que . Sin embargo, es posible organizar puntos de control para garantizar varios niveles de continuidad entre uniones, aunque esto puede generar una pérdida de control local si la restricción es demasiado estricta para el grado dado de la spline de Bézier. ${\ estilo de visualización C^{0}}$

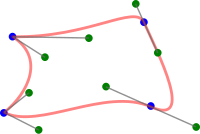
Unión suave de Béziers cúbicos

Dadas dos curvas de Bézier cúbicas con puntos de control y respectivamente, las restricciones para asegurar la continuidad en se pueden definir de la siguiente manera: ${\displaystyle [\mathbf {P}_{0},\mathbf {P}_{1},\mathbf {P}_{2},\mathbf {P}_{3}]}$${\displaystyle [\mathbf {P}_{3},\mathbf {P}_{4},\mathbf {P}_{5},\mathbf {P}_{6}]}$${\ estilo de visualización \ mathbf {P} _ {3}}$

• ${\ estilo de visualización C^{0}/G^{0}}$(continuidad posicional) requiere que se encuentren en el mismo punto, lo que hacen todas las splines de Bézier por definición. En este ejemplo, el punto compartido es${\ estilo de visualización \ mathbf {P} _ {3}}$

• ${\ estilo de visualización C^{1}}$(continuidad de velocidad) requiere que los puntos de control vecinos alrededor de la unión sean espejos entre sí. En otras palabras, deben seguir la restricción de${\displaystyle \mathbf {P} _{4}=2\mathbf {P} _{3}-\mathbf {P} _{2}}$

• ${\ estilo de visualización G^{1}}$(continuidad tangente) requiere que los puntos de control vecinos sean colineales con la unión. Esto es menos estricto que la continuidad, dejando un grado extra de libertad que se puede parametrizar usando un escalar . La restricción se puede expresar entonces por${\ estilo de visualización C^{1}}$${\ estilo de visualización \ beta _ {1}}$${\displaystyle \mathbf {P}_{4}=\mathbf {P}_{3}+(\mathbf {P}_{3}-\mathbf {P}_{2})\beta_{1} }$

Si bien las siguientes restricciones de continuidad son posibles, rara vez se usan con splines de Bézier cúbicos, ya que otras splines como B-spline o β-spline manejarán naturalmente restricciones más altas sin pérdida de control local.

• ${\ estilo de visualización C^{2}}$(continuidad de la aceleración) está limitada por . Sin embargo, la aplicación de esta restricción en toda una spline cúbica de Bézier provocará una pérdida de control local en cascada sobre los puntos tangentes. La curva seguirá pasando por uno de cada tres puntos de la spline, pero se perderá el control sobre su forma. Para lograr la continuidad usando curvas cúbicas, se recomienda usar un B-spline uniforme cúbico en su lugar, ya que asegura la continuidad sin pérdida de control local, a expensas de no tener la garantía de pasar por puntos específicos.${\displaystyle \mathbf {P} _{5}=\mathbf {P} _{1}+4(\mathbf {P} _{3}-\mathbf {P} _{2})}$${\ estilo de visualización C^{2}}$${\ estilo de visualización C^{2}}$

• ${\ estilo de visualización G^{2}}$(continuidad de curvatura) está restringida por , dejando dos grados de libertad en comparación con , en forma de dos escalares y . Son posibles grados más altos de continuidad geométrica, aunque se vuelven cada vez más complejos.${\displaystyle \mathbf {P}_{5}=\mathbf {P}_{3}+(\mathbf {P}_{3}-\mathbf {P}_{2})(2\beta_{ 1}+\beta _{1}^{2}+\beta _{2}/2)+(\mathbf {P} _{1}-\mathbf {P} _{2})\beta _{1 }^{2}}$${\ estilo de visualización C^{2}}$${\ estilo de visualización \ beta _ {1}}$${\ estilo de visualización \ beta _ {2}}$

• ${\ estilo de visualización C^{3}}$(continuidad de la sacudida) está restringida por . La aplicación de esta restricción a la spline cúbica de Bézier provocará una pérdida total del control local, ya que ahora toda la spline está completamente restringida y definida por los puntos de control de la primera curva. De hecho, podría decirse que ya no es una spline, ya que su forma ahora es equivalente a extrapolar la primera curva indefinidamente, haciéndola no solo continua, sino también, ya que las uniones entre curvas separadas ya no existen.${\displaystyle \mathbf {P}_{6}=\mathbf {P}_{3}+(\mathbf {P}_{3}-\mathbf {P}_{0})+6(\mathbf { P}_{1}-\mathbf {P}_{2}+\mathbf {P}_{3}-\mathbf {P}_{2})}$${\ estilo de visualización C^{3}}$${\displaystyle C^{\infty}}$

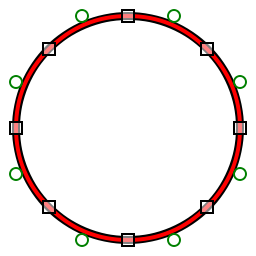
Aproximación de arcos circulares

En caso de que las primitivas de arco circular no se admitan en un entorno particular, se pueden aproximar mediante curvas de Bézier . Comúnmente, se usan ocho segmentos cuadráticos o cuatro segmentos cúbicos para aproximar un círculo. Es deseable encontrar la longitud de los puntos de control que resulten en el menor error de aproximación para un número dado de segmentos cúbicos. ${\ estilo de visualización \ mathbf {k}}$

Usando cuatro curvas

Considerando solo el arco de circunferencia unitaria de 90 grados en el primer cuadrante , definimos los extremos y con los puntos de control y , respectivamente, como: ${\ estilo de visualización \ mathbf {A}}$${\ estilo de visualización \ mathbf {B}}$${\displaystyle \mathbf {A'} }$${\displaystyle \mathbf {B'} }$

${\displaystyle {\begin{alineado}\mathbf {A} &=[0,1]\\\mathbf {A'} &=[\mathbf {k} ,1]\\\mathbf {B'} &= [1,\mathbf {k} ]\\\mathbf {B} &=[1,0]\\\end{alineado}}}$

De la definición de la curva de Bézier cúbica, tenemos:

${\displaystyle \mathbf {C} (t)=(1-t)^{3}\mathbf {A} +3(1-t)^{2}t\mathbf {A'} +3(1-t) )t^{2}\mathbf {B'} +t^{3}\mathbf {B} }$

Con el punto como el punto medio del arco, podemos escribir las siguientes dos ecuaciones: ${\ estilo de visualización \ mathbf {C} (t = 0,5)}$

${\displaystyle {\begin{alineado}\mathbf {C} &={\frac {1}{8}}\mathbf {A} +{\frac {3}{8}}\mathbf {A'} +{ \frac {3}{8}}\mathbf {B'} +{\frac {1}{8}}\mathbf {B} \\\mathbf {C} &={\raíz cuadrada {1/2}}= {\sqrt {2}}/2\end{alineado}}}$

Resolviendo estas ecuaciones para la coordenada x (e idénticamente para la coordenada y) se obtiene:

${\displaystyle {\frac {0}{8}}\mathbf {+} {\frac {3}{8}}\mathbf {k} +{\frac {3}{8}}+{\frac {1 {8}}={\raíz cuadrada {2}}/2}$

${\displaystyle \mathbf {k} ={\frac {4}{3}}({\sqrt {2}}-1)\aprox. 0,5522847498}$

Sin embargo, tenga en cuenta que la curva de Bézier resultante está completamente fuera del círculo, con una desviación máxima del radio de aproximadamente 0,00027. Añadiendo una pequeña corrección a puntos intermedios como

${\displaystyle {\begin{alineado}\mathbf {A'} &=[\mathbf {k} +0.0009,1-0.00103]\\\mathbf {B'} &=[1-0.00103,\mathbf {k} +0.0009],\end{alineado}}}$

la magnitud de la desviación del radio a 1 se reduce en un factor de aproximadamente 3, a 0,000068 (a expensas de la derivabilidad de la curva circular aproximada en los puntos finales).

Caso general

Podemos componer un círculo de radio a partir de un número arbitrario de curvas cúbicas de Bézier. Deje que el arco comience en el punto y termine en el punto , colocados a distancias iguales por encima y por debajo del eje x, abarcando un arco de ángulo : ${\ estilo de visualización R}$${\ estilo de visualización \ mathbf {A}}$${\ estilo de visualización \ mathbf {B}}$${\ estilo de visualización \ theta = 2 \ phi}$

${\displaystyle {\begin{alineado}\mathbf {A}_{x}&=R\cos(\phi )\\\mathbf {A}_{y}&=R\sin(\phi )\\\ mathbf {B} _{x}&=\mathbf {A} _{x}\\\mathbf {B} _{y}&=-\mathbf {A} _{y}\end{alineado}}}$

Los puntos de control se pueden escribir como:

${\displaystyle {\begin{alineado}\mathbf {A'} _{x}&={\frac {4R-\mathbf {A} _{x}}{3}}\\\mathbf {A'} _ {y}&={\frac {(R-\mathbf {A} _{x})(3R-\mathbf {A} _{x})}{3\mathbf {A} _{y}}}\ \\mathbf {B'} _ {x}&=\mathbf {A'} _ {x}\\\mathbf {B'} _ {y}&=-\mathbf {A'} _ {y}\end {alineado}}}$

Ejemplos

• 

  Polybezier cuadrático de ocho segmentos (rojo) que se aproxima a un círculo (negro) con puntos de control

• 

  Polybezier cúbico de cuatro segmentos (rojo) que se aproxima a un círculo (negro) con puntos de control

fuentes

Las fuentes TrueType utilizan Béziers compuestas de curvas Bézier cuadráticas (curvas de segundo orden). Para describir un diseño tipográfico típico como una fuente de computadora con cualquier precisión dada, los Beziers de tercer orden requieren menos datos que los Beziers de segundo orden; y estos a su vez requieren menos datos que una serie de líneas rectas. Esto es cierto aunque cualquier segmento de línea recta requiere menos datos que cualquier segmento de una parábola; y ese segmento parabólico, a su vez, requiere menos datos que cualquier segmento de una curva de tercer orden.

Ver también

• B-spline

Referencias