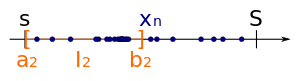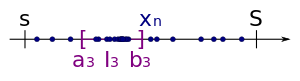Teorema de Bolzano-Weierstrass - Bolzano–Weierstrass theorem
En matemáticas , específicamente en el análisis real , el teorema de Bolzano-Weierstrass , llamado así por Bernard Bolzano y Karl Weierstrass , es un resultado fundamental sobre la convergencia en un espacio euclidiano de dimensión finita R n . El teorema establece que cada secuencia acotada en R n tiene una subsecuencia convergente . Una formulación equivalente es que un subconjunto de R n es secuencialmente compacto si y solo si está cerrado y acotado. El teorema a veces se denomina teorema de compacidad secuencial .
Historia y significado
El teorema de Bolzano-Weierstrass lleva el nombre de los matemáticos Bernard Bolzano y Karl Weierstrass . En realidad, Bolzano lo demostró por primera vez en 1817 como un lema en la demostración del teorema del valor intermedio . Unos cincuenta años después, el resultado fue identificado como significativo por derecho propio, y Weierstrass lo demostró nuevamente. Desde entonces se ha convertido en un teorema esencial de análisis .
Prueba
Primero demostramos el teorema para (conjunto de todos los números reales ), en cuyo caso se puede hacer un buen uso del ordenamiento . De hecho, tenemos el siguiente resultado:
Lema : Cada secuencia infinita en tiene una subsecuencia monótona .
Prueba : Llamemos a un índice de valor entero positivo de una secuencia un "pico" de la secuencia cuando para cada . Supongamos primero que la secuencia tiene infinitos picos, lo que significa que hay una subsecuencia con los siguientes índices y los siguientes términos . Entonces, la secuencia infinita en tiene una subsecuencia monótona, que es . Pero suponga ahora que solo hay un número finito de picos, sea el pico final y deje que el primer índice de una nueva subsecuencia se establezca en . Entonces no es un pico, ya que viene después del pico final, lo que implica la existencia de con y . Una vez más, viene después del pico final, por lo tanto, hay un lugar con . La repetición de este proceso conduce a una subsecuencia infinita no decreciente , lo que demuestra que cada secuencia infinita en tiene una subsecuencia monótona.
Ahora suponga que uno tiene una secuencia acotada en ; por el lema probado anteriormente existe una subsecuencia monótona, igualmente también acotada. Se deduce del teorema de la convergencia monótona que esta subsecuencia converge.
Finalmente, el caso general ( ), se puede reducir al caso de lo siguiente: dada una secuencia acotada en , la secuencia de primeras coordenadas es una secuencia real acotada, por lo tanto tiene una subsecuencia convergente. Luego, se puede extraer una subsecuencia en la que convergen las segundas coordenadas, y así sucesivamente, hasta que al final hayamos pasado de la secuencia original a una subsecuencia veces, que sigue siendo una subsecuencia de la secuencia original, en la que cada secuencia de coordenadas converge, por lo tanto, la subsecuencia en sí es convergente.
Prueba alternativa
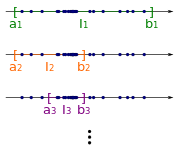
También hay una prueba alternativa del teorema de Bolzano-Weierstrass usando intervalos anidados . Comenzamos con una secuencia acotada :
Debido a que dividimos a la mitad la longitud de un intervalo en cada paso, el límite de la longitud del intervalo es cero. Además, por el teorema de intervalos anidados , que establece que si cada I n es un intervalo cerrado y acotado, digamos
- Yo n = [a n , b n ]
con
- a n ≤ b n
luego, bajo el supuesto de anidamiento, la intersección de I n no está vacía. Por tanto, hay un número que está en cada intervalo . Ahora mostramos, ese es un punto de acumulación de .
Tome un vecindario de . Debido a que la longitud de los intervalos converge a cero, hay un intervalo que es un subconjunto de . Porque contiene por construcción un número infinito de miembros de y , también contiene un número infinito de miembros de . Esto prueba que es un punto de acumulación de . Por lo tanto, hay una subsecuencia de que converge a .
Compacidad secuencial en espacios euclidianos
Supongamos que A es un subconjunto de R n con la propiedad de que cada secuencia en A tiene una subsecuencia convergente a un elemento de A . Entonces A debe estar acotada, ya que de lo contrario existe una secuencia x m en A con || x m || ≥ m para todo m , y luego cada subsecuencia es ilimitada y por lo tanto no convergente. Además, A debe estar cerrado, ya que a partir de un punto no interior x en el complemento de A , se puede construir una secuencia valorada por A que converja ax . Así, los subconjuntos A de R n para los cuales cada secuencia en A tiene una subsecuencia que converge a un elemento de A , es decir, los subconjuntos que son secuencialmente compactos en la topología del subespacio , son precisamente los subconjuntos cerrados y acotados.
Esta forma del teorema aclara especialmente la analogía con el teorema de Heine-Borel , que afirma que un subconjunto de R n es compacto si y sólo si es cerrado y acotado. De hecho, la topología general nos dice que un espacio metrizable es compacto si y solo si es secuencialmente compacto, de modo que los teoremas de Bolzano-Weierstrass y Heine-Borel son esencialmente los mismos.
Aplicación a la economía
Hay diferentes conceptos de equilibrio importantes en economía, cuyas pruebas de existencia a menudo requieren variaciones del teorema de Bolzano-Weierstrass. Un ejemplo es la existencia de una asignación Pareto eficiente . Una asignación es una matriz de paquetes de consumo para agentes en una economía, y una asignación es Pareto eficiente si no se le puede hacer ningún cambio que empeore a ningún agente y al menos a un agente en mejor situación (aquí las filas de la matriz de asignación deben ser clasificable por una relación de preferencia ). El teorema de Bolzano-Weierstrass permite probar que si el conjunto de asignaciones es compacto y no está vacío , entonces el sistema tiene una asignación Pareto-eficiente.
Ver también
- Espacio secuencialmente compacto
- Teorema de Heine-Borel
- Completitud de los números reales
- Principio variacional de Ekeland
Notas
Referencias
- Bartle, Robert G .; Sherbert, Donald R. (2000). Introducción al análisis real (3ª ed.). Nueva York: J. Wiley.
- Fitzpatrick, Patrick M. (2006). Cálculo avanzado (2ª ed.). Belmont, CA: Thomson Brooks / Cole. ISBN 0-534-37603-7.
























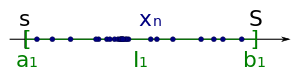
![{\ Displaystyle I_ {1} = [s, S]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58be63fbf6d3dff28ca6747569a558d5af61740e)