Soluciones canónicas de la ecuación general de Legendre
En matemáticas , los polinomios de Legendre asociados son las soluciones canónicas de la ecuación general de Legendre.
-
![(1-x ^ {2}) {\ frac {d ^ {2}} {dx ^ {2}}} P _ {\ ell} ^ {m} (x) -2x {\ frac {d} {dx} } P _ {\ ell} ^ {m} (x) + \ left [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P_ {\ ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d8e4b95ac4a81fd84aa2768d8f6381ca74fabf) ,
,
o equivalente
-
![{\ frac {d} {dx}} \ left [(1-x ^ {2}) {\ frac {d} {dx}} P _ {\ ell} ^ {m} (x) \ right] + \ left [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P _ {\ ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/918ec803eebef3f5df089511e301ce99f1695395) ,
,
donde el índices ℓ y m (que son números enteros) se conocen como el grado y el orden del polinomio de Legendre asociada respectivamente. Esta ecuación tiene soluciones no nulos que son no singular en [-1, 1] sólo si ℓ y m son números enteros con 0 ≤ m ≤ ℓ , o con valores negativos trivialmente equivalentes. Cuando además m es par, la función es un polinomio . Cuando m es cero y ℓ entero, estas funciones son idénticas a los polinomios de Legendre . En general, cuando ℓ y mson números enteros, las soluciones regulares a veces se denominan "polinomios de Legendre asociados", aunque no son polinomios cuando m es impar. La clase completamente general de las funciones con valores complejos de bienes arbitraria o ℓ y m son funciones de Legendre . En ese caso, los parámetros suelen estar etiquetados con letras griegas.
La ecuación diferencial ordinaria de Legendre se encuentra con frecuencia en la física y otros campos técnicos. En particular, ocurre al resolver la ecuación de Laplace (y las ecuaciones diferenciales parciales relacionadas ) en coordenadas esféricas . Los polinomios asociados de Legendre juegan un papel vital en la definición de armónicos esféricos .
Definición de parámetros enteros no negativos ℓ y m
Estas funciones se denotan , donde el superíndice indica la orden, y no una potencia de P . Su definición más sencilla es en términos de derivadas de polinomios ordinarios de Legendre ( m ≥ 0)

-
 ,
,
El factor (−1) m en esta fórmula se conoce como fase de Condon-Shortley . Algunos autores lo omiten. Las funciones descritas por esta ecuación satisfacen la ecuación general diferencial Legendre con los valores indicados de los parámetros ℓ y m sigue diferenciando m veces la ecuación Legendre para P ℓ :

Además, dado que según la fórmula de Rodrigues ,
![P _ {\ ell} (x) = {\ frac {1} {2 ^ {\ ell} \, \ ell!}} \ {\ Frac {d ^ {\ ell}} {dx ^ {\ ell}}} \ left [(x ^ {2} -1) ^ {\ ell} \ right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ca96dae138d4dc21c8eb5ee22e0f3c09d8b2ae)
la Pm
ℓ se puede expresar en la forma

Esta ecuación permite la extensión del rango de ma : - ℓ ≤ m ≤ ℓ . Las definiciones de P ℓ ± m , resultantes de esta expresión por sustitución de ± m , son proporcionales. De hecho, equipare los coeficientes de potencias iguales en el lado izquierdo y derecho de

entonces se sigue que la constante de proporcionalidad es

así que eso

Notaciones alternativas
Las siguientes notaciones alternativas también se utilizan en la literatura:

Forma cerrada
El polinomio de Legendre asociado también se puede escribir como:

con monomios simples y la forma generalizada del coeficiente binomial .
Ortogonalidad
Los polinomios de Legendre asociados no son mutuamente ortogonales en general. Por ejemplo, no es ortogonal a . Sin embargo, algunos subconjuntos son ortogonales. Suponiendo que 0 ≤ m ≤ ℓ , satisfacen la condición de ortogonalidad para m fijo :



Donde δ k , ℓ es el delta de Kronecker .
Además, satisfacen la condición de ortogonalidad para ℓ fijo :

M negativo y / o ℓ negativo
La ecuación diferencial es claramente invariante bajo un cambio de signo de m .
Se mostró anteriormente que las funciones para m negativo son proporcionales a las de m positivo :

(Esto se deriva de la definición de la fórmula de Rodrigues. Esta definición también hace que las diversas fórmulas de recurrencia funcionen para m positiva o negativa ).

La ecuación diferencial también es invariante bajo un cambio de ℓ a - ℓ - 1, y las funciones para ℓ negativo están definidas por
-
 .
.
Paridad
A partir de su definición, se puede verificar que las funciones de Legendre asociadas son pares o impares según

Las primeras funciones asociadas de Legendre
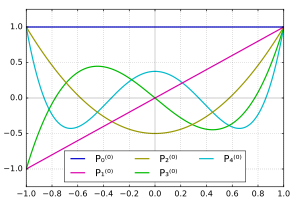
Funciones de Legendre asociadas para m = 0

Funciones de Legendre asociadas para m = 1

Funciones de Legendre asociadas para m = 2
Las primeras funciones de Legendre asociadas, incluidas aquellas para valores negativos de m , son:

























Fórmula de recurrencia
Estas funciones tienen varias propiedades de repetición:

![2mxP _ {\ ell} ^ {m} (x) = - {\ sqrt {1-x ^ {2}}} \ left [P _ {\ ell} ^ {m + 1} (x) + (\ ell + m ) (\ ell -m + 1) P _ {\ ell} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b8c51959e61b723fca74ad217ca195809a70d1)
![{\ frac {1} {\ sqrt {1-x ^ {2}}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2m}} \ left [P _ {\ ell -1} ^ {m + 1} (x) + (\ ell + m-1) (\ ell + m) P _ {\ ell -1} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e697003e6ca8eba77eafc0ee9584a1bb0f73b97a)
![{\ frac {1} {\ sqrt {1-x ^ {2}}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2m}} \ left [P _ {\ ell +1} ^ {m + 1} (x) + (\ ell -m + 1) (\ ell -m + 2) P _ {\ ell +1} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85ac33b2bfe757e1c5680ce2bcb075febcb0258)
![{\ sqrt {1-x ^ {2}}} P _ {\ ell} ^ {m} (x) = {\ frac {1} {2 \ ell +1}} \ left [(\ ell -m + 1 ) (\ ell -m + 2) P _ {\ ell +1} ^ {m-1} (x) - (\ ell + m-1) (\ ell + m) P _ {\ ell -1} ^ {m -1} (x) \ derecha]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa0b88f261e938f80c8b93576b8bf3e290727722)
![{\ Displaystyle {\ sqrt {1-x ^ {2}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2 \ ell +1}} \ left [P _ {\ ell +1} ^ {m + 1} (x) -P _ {\ ell -1} ^ {m + 1} (x) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a962cf8ad9bbf80839d79f5f0afe89ef6d2c741)


![{\ sqrt {1-x ^ {2}}} {\ frac {d} {dx}} {P _ {\ ell} ^ {m}} (x) = {\ frac {1} {2}} \ left [(\ ell + m) (\ ell -m + 1) P _ {\ ell} ^ {m-1} (x) -P _ {\ ell} ^ {m + 1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba467a53fecf20a7cd085d7b7de07a89b565e74)
![(1-x ^ {2}) {\ frac {d} {dx}} {P _ {\ ell} ^ {m}} (x) = {\ frac {1} {2 \ ell +1}} \ left [(\ ell +1) (\ ell + m) P _ {\ ell -1} ^ {m} (x) - \ ell (\ ell -m + 1) P _ {\ ell +1} ^ {m} ( x) \ derecha]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c189752c02a82355c76baf09259946997196d2a)




Identidades útiles (valores iniciales para la primera recursión):



con !! el doble factorial .
Fórmula de Gaunt
La integral sobre el producto de tres polinomios de Legendre asociados (con órdenes coincidentes como se muestra a continuación) es un ingrediente necesario cuando se desarrollan productos de polinomios de Legendre en una serie lineal en los polinomios de Legendre. Por ejemplo, esto resulta necesario cuando se realizan cálculos atómicos de la variedad Hartree-Fock donde se necesitan elementos matriciales del operador de Coulomb . Para esto tenemos la fórmula de Gaunt

|

|
|
|

|
Esta fórmula se utilizará bajo los siguientes supuestos:
- los grados son números enteros no negativos

- los tres órdenes son números enteros no negativos

-
 es el mayor de los tres pedidos
es el mayor de los tres pedidos
- los pedidos resumen

- los grados obedecen

Otras cantidades que aparecen en la fórmula se definen como



La integral es cero a menos que
- la suma de grados es par, por lo que es un número entero

- se cumple la condición triangular

Dong y Lemus (2002) generalizaron la derivación de esta fórmula a integrales sobre un producto de un número arbitrario de polinomios de Legendre asociados.
Generalización mediante funciones hipergeométricas
En realidad, estas funciones pueden definirse para argumentos y parámetros complejos generales:
![P _ {\ lambda} ^ {\ mu} (z) = {\ frac {1} {\ Gamma (1- \ mu)}} \ left [{\ frac {1 + z} {1-z}} \ right ] ^ {\ mu / 2} \, _ {2} F_ {1} (- \ lambda, \ lambda +1; 1- \ mu; {\ frac {1-z} {2}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/a33abd8dbaad6ee01cef4e0d064a2ebd78aad53a)
donde es la función gamma y es la función hipergeométrica


Se denominan funciones de Legendre cuando se definen de esta forma más general. Satisfacen la misma ecuación diferencial que antes:
![(1-z ^ {2}) \, y '' - 2zy '+ \ left (\ lambda [\ lambda +1] - {\ frac {\ mu ^ {2}} {1-z ^ {2}} } \ right) \, y = 0. \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/abfb2180fe5518a23933ad4fa6f8ed20bba11855)
Dado que esta es una ecuación diferencial de segundo orden, tiene una segunda solución
, definida como:


 y ambos obedecen a las distintas fórmulas de recurrencia dadas anteriormente.
y ambos obedecen a las distintas fórmulas de recurrencia dadas anteriormente.

Reparametrización en términos de ángulos
Estas funciones son más útiles cuando el argumento se reparametriza en términos de ángulos, dejando :


Usando la relación , la lista dada arriba produce los primeros polinomios, parametrizados de esta manera, como:

![{\ begin {align} P_ {0} ^ {0} (\ cos \ theta) & = 1 \\ [8pt] P_ {1} ^ {0} (\ cos \ theta) & = \ cos \ theta \\ [8pt] P_ {1} ^ {1} (\ cos \ theta) & = - \ sin \ theta \\ [8pt] P_ {2} ^ {0} (\ cos \ theta) & = {\ tfrac {1 } {2}} (3 \ cos ^ {2} \ theta -1) \\ [8pt] P_ {2} ^ {1} (\ cos \ theta) & = - 3 \ cos \ theta \ sin \ theta \ \ [8pt] P_ {2} ^ {2} (\ cos \ theta) & = 3 \ sin ^ {2} \ theta \\ [8pt] P_ {3} ^ {0} (\ cos \ theta) & = {\ tfrac {1} {2}} (5 \ cos ^ {3} \ theta -3 \ cos \ theta) \\ [8pt] P_ {3} ^ {1} (\ cos \ theta) & = - { \ tfrac {3} {2}} (5 \ cos ^ {2} \ theta -1) \ sin \ theta \\ [8pt] P_ {3} ^ {2} (\ cos \ theta) & = 15 \ cos \ theta \ sin ^ {2} \ theta \\ [8pt] P_ {3} ^ {3} (\ cos \ theta) & = - 15 \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {0} (\ cos \ theta) & = {\ tfrac {1} {8}} (35 \ cos ^ {4} \ theta -30 \ cos ^ {2} \ theta +3) \\ [8pt] P_ {4} ^ {1} (\ cos \ theta) & = - {\ tfrac {5} {2}} (7 \ cos ^ {3} \ theta -3 \ cos \ theta) \ sin \ theta \\ [8pt] P_ {4} ^ {2} (\ cos \ theta) & = {\ tfrac {15} {2}} (7 \ cos ^ {2} \ theta -1) \ sin ^ {2} \ theta \\ [8pt] P_ {4} ^ {3} (\ cos \ theta) & = - 105 \ cos \ theta \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {4} (\ cos \ theta) & = 105 \ sin ^ {4} \ theta \ end {alineado}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ddaa2766fcd73e8e64234f1f511089d9e11f97d)
Las relaciones de ortogonalidad dadas anteriormente se vuelven en esta formulación: para m fijo , son ortogonales, parametrizadas por θ sobre , con peso :

![[0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)


Además, para fijo ℓ :

En términos de θ, ¿ son soluciones de

![{\ frac {d ^ {2} y} {d \ theta ^ {2}}} + \ cot \ theta {\ frac {dy} {d \ theta}} + \ left [\ lambda - {\ frac {m ^ {2}} {\ sin ^ {2} \ theta}} \ right] \, y = 0 \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf734246861cd768b5d9f61be5f5f3b0f3f502f5)
Más precisamente, dado un número entero m 0, la ecuación anterior tiene soluciones no singulares solo cuando para ℓ
un número entero ≥ m , y esas soluciones son proporcionales a
.



Aplicaciones en física: armónicos esféricos
En muchas ocasiones en la física , los polinomios de Legendre asociados en términos de ángulos ocurren donde está involucrada la simetría esférica . El ángulo de colatitud en coordenadas esféricas es el ángulo utilizado anteriormente. El ángulo de longitud`` aparece en un factor de multiplicación. Juntos, hacen un conjunto de funciones llamadas armónicos esféricos . Estas funciones expresan la simetría de las dos esferas bajo la acción del grupo de Lie SO (3).


Lo que hace que estas funciones sean útiles es que son fundamentales para la solución de la ecuación
en la superficie de una esfera. En coordenadas esféricas θ (colatitude) y φ (longitud), el laplaciano es


Cuando la ecuación diferencial parcial

se resuelve mediante el método de separación de variables , se obtiene una parte dependiente de φ o para el entero m≥0, y una ecuación para la parte dependiente de θ


![{\ frac {d ^ {2} y} {d \ theta ^ {2}}} + \ cot \ theta {\ frac {dy} {d \ theta}} + \ left [\ lambda - {\ frac {m ^ {2}} {\ sin ^ {2} \ theta}} \ right] \, y = 0 \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf734246861cd768b5d9f61be5f5f3b0f3f502f5)
para lo cual las soluciones están con
y .



Por tanto, la ecuación

tiene soluciones separadas no singulares solo cuando , y esas soluciones son proporcionales a


y

Para cada elección de ℓ , hay 2ℓ + 1 funciones para los diversos valores de my opciones de seno y coseno. Todos son ortogonales tanto en ℓ como en m cuando se integran sobre la superficie de la esfera.
Las soluciones generalmente se escriben en términos de exponenciales complejos :

Las funciones son los armónicos esféricos y la cantidad en la raíz cuadrada es un factor de normalización. Recordando la relación entre las funciones de Legendre asociadas de m positivo y negativo , se muestra fácilmente que los armónicos esféricos satisfacen la identidad


Las funciones armónicas esféricas forman un conjunto completo de funciones ortonormales en el sentido de la serie de Fourier . Los trabajadores de los campos de la geodesia, el geomagnetismo y el análisis espectral utilizan una fase y un factor de normalización diferentes a los que se dan aquí (ver armónicos esféricos ).
Cuando una ecuación diferencial parcial esféricamente simétrica tridimensional se resuelve mediante el método de separación de variables en coordenadas esféricas, la parte que queda después de la eliminación de la parte radial es típicamente de la forma

y por tanto las soluciones son armónicos esféricos.
Generalizaciones
Los polinomios de Legendre están estrechamente relacionados con las series hipergeométricas . En forma de armónicos esféricos, expresan la simetría de las dos esferas bajo la acción del grupo de Lie SO (3). Hay muchos otros grupos de Lie además de SO (3), y existe una generalización análoga de los polinomios de Legendre para expresar las simetrías de los grupos de Lie semi-simples y los espacios simétricos de Riemann . Hablando crudamente, se puede definir un laplaciano en espacios simétricos; las funciones propias del laplaciano pueden considerarse como generalizaciones de los armónicos esféricos a otros entornos.
Ver también
notas y referencias
-
Arfken, GB; Weber, HJ (2001), Métodos matemáticos para físicos , Academic Press, ISBN 978-0-12-059825-0; Sección 12.5. (Utiliza una convención de signos diferente).
-
Belousov, SL (1962), Tablas de polinomios de Legendre asociados normalizados , Tablas matemáticas, 18 , Pergamon Press.
-
Condon, UE; Shortley, GH (1970), La teoría de los espectros atómicos , Cambridge, Inglaterra: Cambridge University Press, OCLC 5388084; Capítulo 3.
-
Courant, Richard ; Hilbert, David (1953), Métodos de física matemática, Volumen 1 , Nueva York: Interscience Publischer, Inc.
-
Dunster, TM (2010), "Legendre y funciones relacionadas" , en Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
-
Edmonds, AR (1957), Momento angular en mecánica cuántica , Princeton University Press, ISBN 978-0-691-07912-7; Capitulo 2.
-
Hildebrand, FB (1976), Cálculo avanzado para aplicaciones , Prentice Hall, ISBN 978-0-13-011189-0.
-
Koornwinder, Tom H .; Wong, Roderick SC; Koekoek, Roelof; Swarttouw, René F. (2010), "Polinomios ortogonales" , en Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- Schach, SR (1973) Nuevas identidades para las funciones asociadas de Legendre de orden integral y grado , Revista de la Sociedad de Matemáticas Industriales y Aplicadas sobre Análisis Matemático, 1976, Vol. 7, núm. 1: págs. 59, 69
enlaces externos

![(1-x ^ {2}) {\ frac {d ^ {2}} {dx ^ {2}}} P _ {\ ell} ^ {m} (x) -2x {\ frac {d} {dx} } P _ {\ ell} ^ {m} (x) + \ left [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P_ {\ ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d8e4b95ac4a81fd84aa2768d8f6381ca74fabf)
![{\ frac {d} {dx}} \ left [(1-x ^ {2}) {\ frac {d} {dx}} P _ {\ ell} ^ {m} (x) \ right] + \ left [\ ell (\ ell +1) - {\ frac {m ^ {2}} {1-x ^ {2}}} \ right] P _ {\ ell} ^ {m} (x) = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/918ec803eebef3f5df089511e301ce99f1695395)



![P _ {\ ell} (x) = {\ frac {1} {2 ^ {\ ell} \, \ ell!}} \ {\ Frac {d ^ {\ ell}} {dx ^ {\ ell}}} \ left [(x ^ {2} -1) ^ {\ ell} \ right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/43ca96dae138d4dc21c8eb5ee22e0f3c09d8b2ae)











































![2mxP _ {\ ell} ^ {m} (x) = - {\ sqrt {1-x ^ {2}}} \ left [P _ {\ ell} ^ {m + 1} (x) + (\ ell + m ) (\ ell -m + 1) P _ {\ ell} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/16b8c51959e61b723fca74ad217ca195809a70d1)
![{\ frac {1} {\ sqrt {1-x ^ {2}}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2m}} \ left [P _ {\ ell -1} ^ {m + 1} (x) + (\ ell + m-1) (\ ell + m) P _ {\ ell -1} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e697003e6ca8eba77eafc0ee9584a1bb0f73b97a)
![{\ frac {1} {\ sqrt {1-x ^ {2}}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2m}} \ left [P _ {\ ell +1} ^ {m + 1} (x) + (\ ell -m + 1) (\ ell -m + 2) P _ {\ ell +1} ^ {m-1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/a85ac33b2bfe757e1c5680ce2bcb075febcb0258)
![{\ sqrt {1-x ^ {2}}} P _ {\ ell} ^ {m} (x) = {\ frac {1} {2 \ ell +1}} \ left [(\ ell -m + 1 ) (\ ell -m + 2) P _ {\ ell +1} ^ {m-1} (x) - (\ ell + m-1) (\ ell + m) P _ {\ ell -1} ^ {m -1} (x) \ derecha]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa0b88f261e938f80c8b93576b8bf3e290727722)
![{\ Displaystyle {\ sqrt {1-x ^ {2}}} P _ {\ ell} ^ {m} (x) = {\ frac {-1} {2 \ ell +1}} \ left [P _ {\ ell +1} ^ {m + 1} (x) -P _ {\ ell -1} ^ {m + 1} (x) \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a962cf8ad9bbf80839d79f5f0afe89ef6d2c741)


![{\ sqrt {1-x ^ {2}}} {\ frac {d} {dx}} {P _ {\ ell} ^ {m}} (x) = {\ frac {1} {2}} \ left [(\ ell + m) (\ ell -m + 1) P _ {\ ell} ^ {m-1} (x) -P _ {\ ell} ^ {m + 1} (x) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba467a53fecf20a7cd085d7b7de07a89b565e74)
![(1-x ^ {2}) {\ frac {d} {dx}} {P _ {\ ell} ^ {m}} (x) = {\ frac {1} {2 \ ell +1}} \ left [(\ ell +1) (\ ell + m) P _ {\ ell -1} ^ {m} (x) - \ ell (\ ell -m + 1) P _ {\ ell +1} ^ {m} ( x) \ derecha]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c189752c02a82355c76baf09259946997196d2a)




















![P _ {\ lambda} ^ {\ mu} (z) = {\ frac {1} {\ Gamma (1- \ mu)}} \ left [{\ frac {1 + z} {1-z}} \ right ] ^ {\ mu / 2} \, _ {2} F_ {1} (- \ lambda, \ lambda +1; 1- \ mu; {\ frac {1-z} {2}})](https://wikimedia.org/api/rest_v1/media/math/render/svg/a33abd8dbaad6ee01cef4e0d064a2ebd78aad53a)



![(1-z ^ {2}) \, y '' - 2zy '+ \ left (\ lambda [\ lambda +1] - {\ frac {\ mu ^ {2}} {1-z ^ {2}} } \ right) \, y = 0. \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/abfb2180fe5518a23933ad4fa6f8ed20bba11855)






![{\ begin {align} P_ {0} ^ {0} (\ cos \ theta) & = 1 \\ [8pt] P_ {1} ^ {0} (\ cos \ theta) & = \ cos \ theta \\ [8pt] P_ {1} ^ {1} (\ cos \ theta) & = - \ sin \ theta \\ [8pt] P_ {2} ^ {0} (\ cos \ theta) & = {\ tfrac {1 } {2}} (3 \ cos ^ {2} \ theta -1) \\ [8pt] P_ {2} ^ {1} (\ cos \ theta) & = - 3 \ cos \ theta \ sin \ theta \ \ [8pt] P_ {2} ^ {2} (\ cos \ theta) & = 3 \ sin ^ {2} \ theta \\ [8pt] P_ {3} ^ {0} (\ cos \ theta) & = {\ tfrac {1} {2}} (5 \ cos ^ {3} \ theta -3 \ cos \ theta) \\ [8pt] P_ {3} ^ {1} (\ cos \ theta) & = - { \ tfrac {3} {2}} (5 \ cos ^ {2} \ theta -1) \ sin \ theta \\ [8pt] P_ {3} ^ {2} (\ cos \ theta) & = 15 \ cos \ theta \ sin ^ {2} \ theta \\ [8pt] P_ {3} ^ {3} (\ cos \ theta) & = - 15 \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {0} (\ cos \ theta) & = {\ tfrac {1} {8}} (35 \ cos ^ {4} \ theta -30 \ cos ^ {2} \ theta +3) \\ [8pt] P_ {4} ^ {1} (\ cos \ theta) & = - {\ tfrac {5} {2}} (7 \ cos ^ {3} \ theta -3 \ cos \ theta) \ sin \ theta \\ [8pt] P_ {4} ^ {2} (\ cos \ theta) & = {\ tfrac {15} {2}} (7 \ cos ^ {2} \ theta -1) \ sin ^ {2} \ theta \\ [8pt] P_ {4} ^ {3} (\ cos \ theta) & = - 105 \ cos \ theta \ sin ^ {3} \ theta \\ [8pt] P_ {4} ^ {4} (\ cos \ theta) & = 105 \ sin ^ {4} \ theta \ end {alineado}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ddaa2766fcd73e8e64234f1f511089d9e11f97d)

![[0, \ pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)



![{\ frac {d ^ {2} y} {d \ theta ^ {2}}} + \ cot \ theta {\ frac {dy} {d \ theta}} + \ left [\ lambda - {\ frac {m ^ {2}} {\ sin ^ {2} \ theta}} \ right] \, y = 0 \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf734246861cd768b5d9f61be5f5f3b0f3f502f5)
















