Distribución estable - Stable distribution

Estable

Función de densidad de probabilidad Distribuciones estables α simétricas con factor de escala unitario Distribuciones estables centradas sesgadas con factor de escala unitario
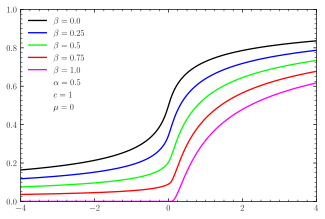
Función de distribución acumulativa CDF para distribuciones estables α simétricas CDF para distribuciones estables centradas asimétricas
Parámetros	α ∈ (0, 2] - parámetro de estabilidad β ∈ [−1, 1] - parámetro de asimetría (tenga en cuenta que la asimetría no está definida) c ∈ (0, ∞) - parámetro de escala μ ∈ (−∞, ∞) - parámetro de ubicación
Apoyo	x ∈ [ μ , + ∞) si α <1 y β = 1 x ∈ (-∞, μ ] si α <1 y β = −1 x ∈ R de lo contrario
PDF	no expresable analíticamente, excepto para algunos valores de parámetros
CDF	no expresable analíticamente, excepto para ciertos valores de parámetros
Significar	μ cuando α > 1 , de lo contrario indefinido
Mediana	μ cuando β = 0 , de lo contrario no se puede expresar analíticamente
Modo	μ cuando β = 0 , de lo contrario no se puede expresar analíticamente
Diferencia	2 c 2 cuando α = 2 , de lo contrario infinito
Oblicuidad	0 cuando α = 2 , de lo contrario indefinido
Ex. curtosis	0 cuando α = 2 , de lo contrario indefinido
Entropía	no expresable analíticamente, excepto para ciertos valores de parámetros
MGF	${\ Displaystyle \ exp \! \ left (t \ mu + c ^ {2} t ^ {2} \ right)}$cuando , de lo contrario, indefinido${\ Displaystyle \ alpha = 2}$
CF	${\ Displaystyle \ exp \! {\ Big [} \; it \ mu - | c \, t | ^ {\ alpha} \, (1-i \ beta \ operatorname {sgn} (t) \ Phi) \; {\Grande ]},}$ dónde ${\ Displaystyle \ Phi = {\ begin {cases} \ tan {\ tfrac {\ pi \ alpha} {2}} & {\ text {if}} \ alpha \ neq 1 \\ - {\ tfrac {2} { \ pi}} \ log | c \, t | & {\ text {if}} \ alpha = 1 \ end {cases}}}$

En la teoría de la probabilidad , se dice que una distribución es estable si una combinación lineal de dos variables aleatorias independientes con esta distribución tiene la misma distribución, hasta los parámetros de ubicación y escala . Se dice que una variable aleatoria es estable si su distribución es estable. La familia de distribución estable también se conoce a veces como la distribución alfa estable de Lévy , en honor a Paul Lévy , el primer matemático que la estudió.

De los cuatro parámetros que definen a la familia, la mayor parte de la atención se ha centrado en el parámetro de estabilidad, α (ver panel). Las distribuciones estables tienen 0 < α ≤ 2 , con el límite superior correspondiente a la distribución normal y α = 1 a la distribución de Cauchy . Las distribuciones tienen una varianza indefinida para α <2 y una media indefinida para α ≤ 1 . La importancia de las distribuciones de probabilidad estables es que son " atractores " para sumas correctamente normalizadas de variables aleatorias independientes e idénticamente distribuidas ( iid ). La distribución normal define una familia de distribuciones estables. Según el teorema clásico del límite central, la suma correctamente normalizada de un conjunto de variables aleatorias, cada una con varianza finita, tenderá a una distribución normal a medida que aumenta el número de variables. Sin el supuesto de varianza finita, el límite puede ser una distribución estable que no es normal. Mandelbrot se refirió a tales distribuciones como "distribuciones paretianas estables", en honor a Vilfredo Pareto . En particular, se refirió a aquellos con un sesgo máximo en la dirección positiva con 1 < α <2 como "distribuciones de Pareto-Lévy", que consideró como mejores descripciones de los precios de las acciones y los productos básicos que las distribuciones normales.

Definición

Una distribución no degenerada es una distribución estable si satisface la siguiente propiedad:

Dejar que X ₁ y X ₂ copias ser independiente de una variable aleatoria X . Entonces se dice que X es estable si para cualquier constante a > 0 y b > 0 la variable aleatoria aX ₁ + bX ₂ tiene la misma distribución que cX + d para algunas constantes c > 0 y d . Se dice que la distribución es estrictamente estable si esto se cumple con d = 0 .

Dado que la distribución normal , la distribución de Cauchy y la distribución de Lévy tienen todas la propiedad anterior, se deduce que son casos especiales de distribuciones estables.

Tales distribuciones forman una familia de cuatro parámetros de continuas distribuciones de probabilidad parametrizada por localización y escala parámetros mu y c , respectivamente, y dos parámetros de forma ß y α , que corresponde aproximadamente a las medidas de asimetría y la concentración, respectivamente (véase las figuras).

La función característica φ ( t ) de cualquier distribución de probabilidad es solo la transformada de Fourier de su función de densidad de probabilidad f ( x ). Por tanto, la función de densidad es la transformada de Fourier inversa de la función característica.

${\ Displaystyle f (x) = {\ frac {1} {2 \ pi}} \ int _ {- \ infty} ^ {\ infty} \ varphi (t) e ^ {- ixt} \, dt}$

Aunque la función de densidad de probabilidad para una distribución estable general no se puede escribir analíticamente, la función característica general se puede expresar analíticamente. Una variable aleatoria X se llama estable si su función característica se puede escribir como

${\ Displaystyle \ varphi (t; \ alpha, \ beta, c, \ mu) = \ exp \ left (it \ mu - | ct | ^ {\ alpha} \ left (1-i \ beta \ operatorname {sgn} (t) \ Phi \ derecha) \ derecha)}$

donde sgn ( t ) es la señal de t y

${\ Displaystyle \ Phi = {\ begin {cases} \ tan \ left ({\ frac {\ pi \ alpha} {2}} \ right) & \ alpha \ neq 1 \\ - {\ frac {2} {\ pi}} \ log | ct | & \ alpha = 1 \ end {cases}}}$

μ ∈ R es un parámetro de desplazamiento, β ∈ [−1, 1], llamado parámetro de asimetría , es una medida de asimetría. Observe que en este contexto la asimetría habitual no está bien definida, ya que para α <2 la distribución no admite segundos momentos o más , y la definición de asimetría habitual es el tercer momento central .

La razón por la que esto da una distribución estable es que la función característica para la suma de dos variables aleatorias independientes es igual al producto de las dos funciones características correspondientes. Agregar dos variables aleatorias de una distribución estable da algo con los mismos valores de α y β , pero posiblemente con valores diferentes de μ y c .

No todas las funciones son la función característica de una distribución de probabilidad legítima (es decir, una cuya función de distribución acumulativa es real y va de 0 a 1 sin disminuir), pero las funciones características dadas anteriormente serán legítimas siempre que los parámetros estén en su rangos. El valor de la función característica en algún valor t es el complejo conjugado de su valor en - t como debería ser para que la función de distribución de probabilidad sea real.

En el caso más simple β = 0 , la función característica es solo una función exponencial estirada ; la distribución es simétrica alrededor de μ y se denomina distribución alfa estable simétrica (Lévy) , a menudo abreviada como SαS .

Cuando α <1 y β = 1, la distribución está respaldada por [ μ , ∞).

El parámetro c > 0 es un factor de escala que es una medida del ancho de la distribución, mientras que α es el exponente o índice de la distribución y especifica el comportamiento asintótico de la distribución.

Parametrizaciones

La definición anterior es solo una de las parametrizaciones en uso para distribuciones estables; es el más común pero no es continuo en los parámetros en α = 1 .

Una parametrización continua es

${\ Displaystyle \ varphi (t; \ alpha, \ beta, \ gamma, \ delta) = \ exp \ left (it \ delta - | \ gamma t | ^ {\ alpha} \ left (1-i \ beta \ operatorname {sgn} (t) \ Phi \ right) \ right)}$

dónde:

${\ Displaystyle \ Phi = {\ begin {cases} \ left (| \ gamma t | ^ {1- \ alpha} -1 \ right) \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ right) & \ alpha \ neq 1 \\ - {\ frac {2} {\ pi}} \ log | \ gamma t | & \ alpha = 1 \ end {cases}}}$

Los rangos de α y β son los mismos que antes, γ (como c ) debería ser positivo y δ (como μ ) debería ser real.

En cualquier parametrización se puede hacer una transformación lineal de la variable aleatoria para obtener una variable aleatoria cuya densidad es . En la primera parametrización, esto se hace definiendo la nueva variable: ${\ Displaystyle f (y; \ alpha, \ beta, 1,0)}$

${\ Displaystyle y = {\ begin {cases} {\ frac {x- \ mu} {\ gamma}} & \ alpha \ neq 1 \\ {\ frac {x- \ mu} {\ gamma}} - \ beta {\ frac {2} {\ pi}} \ ln \ gamma & \ alpha = 1 \ end {cases}}}$

Para la segunda parametrización, simplemente usamos

${\ Displaystyle y = {\ frac {x- \ delta} {\ gamma}}}$

no importa lo que sea α . En la primera parametrización, si existe la media (es decir, α > 1 ) entonces es igual a μ , mientras que en la segunda parametrización cuando existe la media es igual a${\ Displaystyle \ delta - \ beta \ gamma \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ right).}$

La distribución

Por lo tanto, los cuatro parámetros anteriores especifican una distribución estable. Se puede demostrar que cualquier distribución estable no degenerada tiene una función de densidad uniforme (infinitamente diferenciable). Si denota la densidad de X e Y es la suma de copias independientes de X : ${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

${\ Displaystyle Y = \ sum _ {i = 1} ^ {N} k_ {i} (X_ {i} - \ mu) \,}$

entonces Y tiene la densidad con ${\ displaystyle {\ tfrac {1} {s}} f (y / s; \ alpha, \ beta, c, 0)}$

${\ Displaystyle s = \ left (\ sum _ {i = 1} ^ {N} | k_ {i} | ^ {\ alpha} \ right) ^ {\ frac {1} {\ alpha}}}$

El comportamiento asintótico se describe, para α <2, por:

${\ Displaystyle f (x) \ sim {\ frac {1} {| x | ^ {1+ \ alpha}}} \ left (c ^ {\ alpha} (1+ \ operatorname {sgn} (x) \ beta ) \ sin \ left ({\ frac {\ pi \ alpha} {2}} \ right) {\ frac {\ Gamma (\ alpha +1)} {\ pi}} \ right)}$

donde Γ es la función Gamma (excepto que cuando α ≥ 1 y β = ± 1, la cola no se desvanece a la izquierda o derecha, respectivamente, de μ , aunque la expresión anterior es 0). Este comportamiento de " cola pesada " hace que la varianza de las distribuciones estables sea infinita para todo α <2. Esta propiedad se ilustra en las gráficas logarítmicas a continuación.

Cuando α = 2, la distribución es gaussiana (véase más adelante), con las colas asintóticos a exp (- x ² /4 c ² ) / (2 c √π).

Distribución estable unilateral y distribución de recuento estable

Cuando α <1 y β = 1, la distribución está respaldada por [ μ , ∞). Esta familia se denomina distribución estable unilateral . Su distribución estándar (μ = 0) se define como

${\ Displaystyle L _ {\ alpha} (x) = f \ left (x; \ alpha, 1, \ cos \ left ({\ frac {\ alpha \ pi} {2}} \ right) ^ {1 / \ alpha }, 0 \ right)}$, donde .${\ Displaystyle \ alpha <1}$

Vamos , su función característica es . Así, la forma integral de su PDF es (nota: ) ${\ Displaystyle q = \ exp (-i \ alpha \ pi / 2)}$${\ Displaystyle \ varphi (t; \ alpha) = \ exp \ left (-q | t | ^ {\ alpha} \ right)}$${\ Displaystyle {\ text {Im}} (q) <0}$

${\ Displaystyle {\ begin {alineado} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {- \ infty} ^ {\ infty} e ^ {itx} e ^ {- q | t | ^ {\ alpha}} \, dt \ right] \\ & = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ infty} e ^ {- {\ text {Re}} (q) \, t ^ {\ alpha}} \ sin (tx) \ sin (- {\ text {Im}} (q) \, t ^ {\ alpha}) \, dt, {\ text {o}} \\ & = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ infty} e ^ {- {\ text {Re}} (q ) \, t ^ {\ alpha}} \ cos (tx) \ cos ({\ text {Im}} (q) \, t ^ {\ alpha}) \, dt. \\\ end {alineado}}}$

La integral de doble seno es más eficaz para los muy pequeños . ${\ Displaystyle x}$

Considere la suma de Lévy donde , entonces Y tiene la densidad donde . Establecidos , llegamos a la distribución de recuento estable . Su distribución estándar se define como ${\ Displaystyle Y = \ sum _ {i = 1} ^ {N} X_ {i}}$${\ Displaystyle X_ {i} \ sim L _ {\ alpha} (x)}$${\ Displaystyle {\ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {x} {\ nu}} \ right)}$${\ Displaystyle \ nu = N ^ {1 / \ alpha}}$${\ Displaystyle x = 1}$

${\ Displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu) = {\ frac {\ alpha} {\ Gamma \ left ({\ frac {1} {\ alpha}} \ right)}} { \ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {1} {\ nu}} \ right)}$, donde y .${\ Displaystyle \ nu> 0}$${\ Displaystyle \ alpha <1}$

La distribución de recuento estable es el conjugado anterior a la distribución estable unilateral. Su familia de escala de ubicación se define como

${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu; \ nu _ {0}, \ theta) = {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha }})}} {\ frac {1} {\ nu - \ nu _ {0}}} L _ {\ alpha} \ left ({\ frac {\ theta} {\ nu - \ nu _ {0}}} \Derecha)}$, Donde , y .${\ Displaystyle \ nu> \ nu _ {0}}$${\ Displaystyle \ theta> 0}$${\ Displaystyle \ alpha <1}$

También es una distribución unilateral compatible con . El parámetro de ubicación es la ubicación de corte, mientras que define su escala. ${\ Displaystyle [\ nu _ {0}, \ infty)}$${\ Displaystyle \ nu _ {0}}$${\ Displaystyle \ theta}$

Cuando , es la distribución de Lévy que es una distribución gamma inversa. Por lo tanto, es una distribución gamma desplazada de forma 3/2 y escala , ${\ Displaystyle \ alpha = {\ frac {1} {2}}}$${\ Displaystyle L _ {\ frac {1} {2}} (x)}$${\ Displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ Displaystyle 4 \ theta}$

${\ Displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta) = {\ frac {1} {4 {\ sqrt {\ pi }} \ theta ^ {3/2}}} (\ nu - \ nu _ {0}) ^ {1/2} e ^ {- {\ frac {\ nu - \ nu _ {0}} {4 \ theta}}}}$, Donde , .${\ Displaystyle \ nu> \ nu _ {0}}$${\ Displaystyle \ theta> 0}$

Su media es y su desviación estándar es . Se hipotetiza que VIX se distribuye como con y (Ver Sección 7 de). Por tanto, la distribución de recuento estable es la distribución marginal de primer orden de un proceso de volatilidad. En este contexto, se denomina "volatilidad piso". ${\ Displaystyle \ nu _ {0} +6 \ theta}$${\ Displaystyle {\ sqrt {24}} \ theta}$${\ Displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ Displaystyle \ nu _ {0} = 10,4}$${\ Displaystyle \ theta = 1.6}$${\ Displaystyle \ nu _ {0}}$

Otro enfoque para derivar la distribución de conteo estable es usar la transformada de Laplace de la distribución estable unilateral, (Sección 2.4 de)

${\ Displaystyle \ int _ {0} ^ {\ infty} e ^ {- zx} L _ {\ alpha} (x) dx = e ^ {- z ^ {\ alpha}}}$, donde .${\ Displaystyle \ alpha <1}$

Sea , y uno puede descomponer la integral en el lado izquierdo como una distribución del producto de una distribución de Laplace estándar y una distribución de recuento estable estándar, ${\ Displaystyle x = 1 / \ nu}$

${\ Displaystyle \ int _ {0} ^ {\ infty} {\ frac {1} {\ nu}} \ left ({\ frac {1} {2}} e ^ {- {\ frac {| z |} {\ nu}}} \ right) \ left ({\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} {\ frac {1} {\ nu}} L_ { \ alpha} ({\ frac {1} {\ nu}}) \ right) d \ nu = {\ frac {1} {2}} {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} e ^ {- | z | ^ {\ alpha}}}$, donde .${\ Displaystyle \ alpha <1}$

Esto se denomina "descomposición lambda" (consulte la sección 4 de) ya que el lado derecho se denominó "distribución lambda simétrica" ​​en los trabajos anteriores de Lihn. Sin embargo, tiene varios nombres más populares, como " distribución de potencia exponencial " o "error generalizado / distribución normal", a los que a menudo se hace referencia cuando α > 1.

El n-ésimo momento de es el -ésimo momento de , Todos los momentos positivos son finitos. Esto de alguna manera resuelve el espinoso problema de los momentos divergentes en la distribución estable. ${\ Displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu)}$${\ Displaystyle - (n + 1)}$${\ Displaystyle L _ {\ alpha} (x)}$

Propiedades

• Todas las distribuciones estables son infinitamente divisibles .
• Con la excepción de la distribución normal ( α = 2), las distribuciones estables son distribuciones leptocurtóticas y de cola pesada .
• Cierre por convolución

Las distribuciones estables se cierran por convolución para un valor fijo de α . Dado que la convolución es equivalente a la multiplicación de la función transformada de Fourier, se deduce que el producto de dos funciones características estables con el mismo α producirá otra función característica similar . El producto de dos funciones características estables viene dado por:

${\ Displaystyle \ exp \ left (it \ mu _ {1} + it \ mu _ {2} - | c_ {1} t | ^ {\ alpha} - | c_ {2} t | ^ {\ alpha} + i \ beta _ {1} | c_ {1} t | ^ {\ alpha} \ operatorname {sgn} (t) \ Phi + i \ beta _ {2} | c_ {2} t | ^ {\ alpha} \ nombre de operador {sgn} (t) \ Phi \ right)}$

Dado que Φ no es una función de las variables μ , c o β, se deduce que estos parámetros para la función convolucionada están dados por:

${\ Displaystyle {\ begin {alineado} \ mu & = \ mu _ {1} + \ mu _ {2} \\ | c | & = \ left (| c_ {1} | ^ {\ alpha} + | c_ {2} | ^ {\ alpha} \ right) ^ {\ frac {1} {\ alpha}} \\ [6pt] \ beta & = {\ frac {\ beta _ {1} | c_ {1} | ^ {\ alpha} + \ beta _ {2} | c_ {2} | ^ {\ alpha}} {| c_ {1} | ^ {\ alpha} + | c_ {2} | ^ {\ alpha}}} \ final {alineado}}}$

En cada caso, se puede demostrar que los parámetros resultantes se encuentran dentro de los intervalos requeridos para una distribución estable.

Un teorema del límite central generalizado

Otra propiedad importante de las distribuciones estables es el papel que desempeñan en un teorema del límite central generalizado . El teorema del límite central establece que la suma de un número de variables aleatorias independientes e idénticamente distribuidas (iid) con varianzas finitas distintas de cero tenderá a una distribución normal a medida que aumenta el número de variables.

Una generalización debida a Gnedenko y Kolmogorov establece que la suma de una serie de variables aleatorias con distribuciones simétricas que tienen colas de ley de potencias ( colas paretianas ), disminuyendo como donde (y por lo tanto con varianza infinita), tenderá a una distribución estable como el número de sumandos crece. Si entonces la suma converge a una distribución estable con un parámetro de estabilidad igual a 2, es decir, una distribución gaussiana. ${\ Displaystyle | x | ^ {- \ alpha -1}}$${\ Displaystyle 0 <\ alpha \ leqslant 2}$${\ Displaystyle f (x; \ alpha, 0, c, 0)}$${\ Displaystyle \ alpha> 2}$

También hay otras posibilidades. Por ejemplo, si la función característica de la variable aleatoria es asintótica para t pequeña (positiva o negativa), entonces podemos preguntarnos cómo varía t con n cuando el valor de la función característica para la suma de n tales variables aleatorias es igual a un valor dado. valor u : ${\ Displaystyle 1 + a | t | ^ {\ alpha} \ ln | t |}$

${\ Displaystyle \ varphi _ {\ text {sum}} = \ varphi ^ {n} = u}$

Suponiendo por el momento que t → 0, tomamos el límite de lo anterior como n → ∞ :

${\ Displaystyle \ ln u = \ lim _ {n \ to \ infty} n \ ln \ varphi = \ lim _ {n \ to \ infty} na | t | ^ {\ alpha} \ ln | t |.}$

Por lo tanto:

${\ Displaystyle {\ begin {alineado} \ ln (\ ln u) & = \ ln \ left (\ lim _ {n \ to \ infty} na | t | ^ {\ alpha} \ ln | t | \ right) \\ [5pt] & = \ lim _ {n \ to \ infty} \ ln \ left (na | t | ^ {\ alpha} \ ln | t | \ right) = \ lim _ {n \ to \ infty} \ left \ {\ ln (na) + \ alpha \ ln | t | + \ ln (\ ln | t |) \ right \} \ end {alineado}}}$

Esto muestra que es asintótico, por lo que, usando la ecuación anterior, tenemos ${\ Displaystyle \ ln | t |}$${\ Displaystyle {\ tfrac {-1} {\ alpha}} \ ln n,}$

${\ Displaystyle | t | \ sim \ left ({\ frac {- \ alpha \ ln u} {na \ ln n}} \ right) ^ {1 / \ alpha}.}$

Esto implica que la suma dividida por

${\ Displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right) ^ {\ frac {1} {\ alpha}}}$

tiene una función característica cuyo valor en algún t ′ va a u (a medida que n aumenta) cuando En otras palabras, la función característica converge puntualmente ay, por lo tanto, según el teorema de continuidad de Lévy, la suma dividida por ${\ Displaystyle t '= (- \ ln u) ^ {\ frac {1} {\ alpha}}.}$${\ Displaystyle \ exp (- (t ') ^ {\ alpha})}$

${\ Displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right) ^ {\ frac {1} {\ alpha}}}$

converge en distribución a la distribución alfa estable simétrica con parámetro de estabilidad y parámetro de escala 1. ${\ Displaystyle \ alpha}$

Esto se puede aplicar a una variable aleatoria cuyas colas disminuyen a medida que . Esta variable aleatoria tiene una media pero la varianza es infinita. Tomemos la siguiente distribución: ${\ Displaystyle | x | ^ {- 3}}$

${\ Displaystyle f (x) = {\ begin {cases} {\ frac {1} {3}} & | x | \ leqslant 1 \\ {\ frac {1} {3}} x ^ {- 3} & | x |> 1 \ end {casos}}}$

Podemos escribir esto como

${\ Displaystyle f (x) = \ int _ {1} ^ {\ infty} {\ frac {2} {w ^ {4}}} h \ left ({\ frac {x} {w}} \ right) dw}$

dónde

${\ Displaystyle h \ left ({\ frac {x} {w}} \ right) = {\ begin {cases} {\ frac {1} {2}} & \ left | {\ frac {x} {w} } \ right | <1, \\ 0 & \ left | {\ frac {x} {w}} \ right |> 1. \ end {cases}}}$

Queremos encontrar los términos principales de la expansión asintótica de la función característica. La función característica de la distribución de probabilidad es entonces la función característica para f ( x ) es ${\ Displaystyle {\ tfrac {1} {w}} h \ left ({\ tfrac {x} {w}} \ right)}$${\ Displaystyle {\ tfrac {\ sin (tw)} {tw}},}$

${\ Displaystyle \ varphi (t) = \ int _ {1} ^ {\ infty} {\ frac {2 \ sin (tw)} {tw ^ {4}}} dw}$

y podemos calcular:

${\ Displaystyle {\ begin {alineado} \ varphi (t) -1 & = \ int _ {1} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ { 3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} { \ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw \\ & = \ int _ {1} ^ { \ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1+ \ left \ {- {\ frac {t ^ {2} w ^ {2}} {3!}} + {\ frac {t ^ {2} w ^ {2}} {3!}} \ right \} \ right] \, dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw }} - 1 \ right] \, dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} - {\ frac {t ^ {2} dw} {3w}} + \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} -1 + {\ frac {t ^ {2} w ^ {2}} {3!}} \ Right] dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] dw \\ & = \ int _ {1} ^ {\ frac {1 } {| t |}} - {\ frac {t ^ {2} dw} {3w}} + \ left \ {\ int _ {0} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {3!} } \ right] dw- \ int _ {0} ^ {1} {\ frac {2} {w ^ {3 }}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {3!}} \ right] dw \ right \ } + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} { tw}} - 1 \ right] dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} - {\ frac {t ^ {2} dw} {3w}} + t ^ {2} \ int _ {0} ^ {1} {\ frac {2} {y ^ {3}}} \ left [{\ frac {\ sin (y)} {y}} - 1 + {\ frac {y ^ {2}} {6}} \ right] dy- \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw + t ^ {2} \ int _ {1} ^ {\ infty } {\ frac {2} {y ^ {3}}} \ left [{\ frac {\ sin (y)} {y}} - 1 \ right] dy \\ & = - {\ frac {t ^ { 2}} {3}} \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {dw} {w}} + t ^ {2} C_ {1} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw + t ^ {2} C_ {2} \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {t ^ {4} w ^ {4} } {5!}} + \ Cdots \ right] dw \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - {\ mathcal {O}} \ left (t ^ {4} \ right) \ end {al igned}}}$

donde y son constantes. Por lo tanto, ${\ Displaystyle C_ {1}, C_ {2}}$${\ Displaystyle C_ {3}}$

${\ Displaystyle \ varphi (t) \ sim 1 + {\ frac {t ^ {2}} {3}} \ ln | t |}$

y de acuerdo con lo dicho anteriormente (y el hecho de que la varianza de f ( x ; 2,0,1,0) es 2), la suma de n instancias de esta variable aleatoria, dividida por , convergerá en distribución a un valor gaussiano. distribución con varianza 1. Pero la varianza en cualquier n particular seguirá siendo infinita. Tenga en cuenta que el ancho de la distribución límite crece más rápido que en el caso en el que la variable aleatoria tiene una varianza finita (en cuyo caso el ancho crece como la raíz cuadrada de n ). El promedio , obtenido al dividir la suma por n , tiende a un gaussiano cuyo ancho se aproxima a cero a medida que n aumenta, de acuerdo con la Ley de los grandes números . ${\ Displaystyle {\ sqrt {n (\ ln n) / 12}},}$

Casos especiales

Gráfico log-log de PDF de distribución estable centrada simétrica que muestra el comportamiento de la ley de potencia para x grande . El comportamiento de la ley de potencia se evidencia por la apariencia en línea recta de la PDF para x grande , con la pendiente igual a - ( α + 1). (La única excepción es para α = 2, en negro, que es una distribución normal).

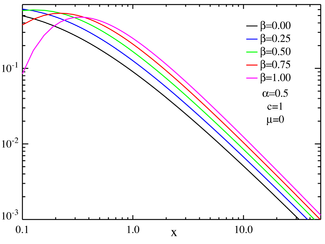
Gráfico log-log de PDF de distribución estable centrada sesgada que muestra el comportamiento de la ley de potencia para x grande . Nuevamente, la pendiente de las porciones lineales es igual a - ( α + 1)

No existe una solución analítica general para la forma de f ( x ). Sin embargo, hay tres casos especiales que pueden expresarse en términos de funciones elementales, como puede verse mediante la inspección de la función característica :

• Para α = 2 la distribución se reduce a una distribución gaussiana con varianza σ ² = 2 c ² y media μ ; el parámetro de asimetría β no tiene ningún efecto.
• Para α = 1 y β = 0, la distribución se reduce a una distribución de Cauchy con el parámetro de escala cy el parámetro de desplazamiento μ .
• Para α = 1/2 y β = 1, la distribución se reduce a una distribución de Lévy con el parámetro de escala cy el parámetro de desplazamiento μ .

Tenga en cuenta que las tres distribuciones anteriores también están conectadas, de la siguiente manera: Una variable aleatoria de Cauchy estándar se puede ver como una mezcla de variables aleatorias gaussianas (todas con media cero), y la varianza se extrae de una distribución de Lévy estándar. Y, de hecho, este es un caso especial de un teorema más general (ver p. 59 de) que permite ver de esta manera cualquier distribución alfa estable simétrica (con el parámetro alfa de la distribución de la mezcla igual al doble del parámetro alfa de la distribución de mezcla (y el parámetro beta de la distribución de mezcla siempre es igual a uno).

Una expresión de forma cerrada general para PDF estables con valores racionales de α está disponible en términos de funciones G de Meijer . Las funciones Fox H también se pueden utilizar para expresar las funciones de densidad de probabilidad estable. Para los números racionales simples, la expresión en forma cerrada suele ser en términos de funciones especiales menos complicadas . Se encuentran disponibles varias expresiones de forma cerrada que tienen expresiones bastante simples en términos de funciones especiales. En la siguiente tabla, los PDF que se pueden expresar mediante funciones elementales se indican con una E y los que se pueden expresar mediante funciones especiales se indican con una s .

Algunos de los casos especiales se conocen por nombres particulares:

• Para α = 1 y β = 1, la distribución es una distribución de Landau que tiene un uso específico en física con este nombre.
• Para α = 3/2 y β = 0, la distribución se reduce a una distribución de Holtsmark con el parámetro de escala cy el parámetro de desplazamiento μ .

Además, en el límite cuando c se acerca a cero o cuando α se acerca a cero, la distribución se acercará a una función delta de Dirac δ ( x  -  μ ) .

Representación de series

La distribución estable se puede reformular como la parte real de una integral más simple:

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0} ^ {\ infty} e ^ {it (x- \ mu)} e ^ {- (ct) ^ {\ alpha} (1-i \ beta \ Phi)} \, dt \ right].}$

Expresando la segunda exponencial como una serie de Taylor , tenemos:

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0} ^ {\ infty} e ^ {it (x- \ mu)} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-qt ^ {\ alpha}) ^ {n}} {n!}} \, dt \ right]}$

donde . Invirtiendo el orden de integración y suma, y ​​realizando la integración se obtiene: ${\ Displaystyle q = c ^ {\ alpha} (1-i \ beta \ Phi)}$

${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1} ^ {\ infty} {\ frac {(-q) ^ {n}} {n!}} \ left ({\ frac {i} {x- \ mu}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \ derecha]}$

que será válido para x ≠ μ y convergerá para valores apropiados de los parámetros. (Tenga en cuenta que el término n = 0 que produce una función delta en x - μ, por lo tanto, se ha eliminado). Expresar la primera exponencial como una serie producirá otra serie en potencias positivas de x - μ que generalmente es menos útil.

Para una distribución estable unilateral, la expansión de la serie anterior debe modificarse, ya que y . No hay una parte real que resumir. En cambio, la integral de la función característica debe realizarse en el eje negativo, lo que da como resultado: ${\ Displaystyle q = \ exp (-i \ alpha \ pi / 2)}$${\ displaystyle qi ^ {\ alpha} = 1}$

${\ Displaystyle {\ begin {alineado} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1} ^ {\ infty} {\ frac {(-q) ^ {n}} {n!}} \ left ({\ frac {-i} {x}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \ right] \\ & = {\ frac {1} {\ pi}} \ sum _ {n = 1} ^ {\ infty} {\ frac {- \ sin (n (\ alpha +1) \ pi)} {n!}} \ left ({\ frac {1} {x}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \\\ end {alineado}}}$

Simulación de variables estables

La simulación de secuencias de variables aleatorias estables no es sencilla, ya que no existen expresiones analíticas para la inversa ni la CDF en sí. Todos los enfoques estándar, como los métodos de rechazo o inversión, requerirían cálculos tediosos. Chambers, Mallows y Stuck (CMS) propusieron una solución mucho más elegante y eficiente, quienes notaron que cierta fórmula integral producía el siguiente algoritmo: ${\ Displaystyle F ^ {- 1} (x)}$${\ Displaystyle F (x)}$

• generar una variable aleatoria distribuida uniformemente y una variable aleatoria exponencial independiente con media 1;${\ Displaystyle U}$${\ Displaystyle \ left (- {\ tfrac {\ pi} {2}}, {\ tfrac {\ pi} {2}} \ right)}$${\ Displaystyle W}$
• para calcular:${\ Displaystyle \ alpha \ neq 1}$

${\ Displaystyle X = \ left (1+ \ zeta ^ {2} \ right) ^ {\ frac {1} {2 \ alpha}} {\ frac {\ sin (\ alpha (U + \ xi))} {( \ cos (U)) ^ {\ frac {1} {\ alpha}}}} \ left ({\ frac {\ cos (U- \ alpha (U + \ xi))} {W}} \ right) ^ { \ frac {1- \ alpha} {\ alpha}},}$

• para calcular:${\ Displaystyle \ alpha = 1}$

${\ Displaystyle X = {\ frac {1} {\ xi}} \ left \ {\ left ({\ frac {\ pi} {2}} + \ beta U \ right) \ tan U- \ beta \ log \ izquierda ({\ frac {{\ frac {\ pi} {2}} W \ cos U} {{\ frac {\ pi} {2}} + \ beta U}} \ right) \ right \},}$

dónde

${\ Displaystyle \ zeta = - \ beta \ tan {\ frac {\ pi \ alpha} {2}}, \ qquad \ xi = {\ begin {cases} {\ frac {1} {\ alpha}} \ arctan ( - \ zeta) & \ alpha \ neq 1 \\ {\ frac {\ pi} {2}} & \ alpha = 1 \ end {cases}}}$

Este algoritmo produce una variable aleatoria . Para obtener una prueba detallada, consulte. ${\ Displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

Dadas las fórmulas para la simulación de una variable aleatoria estable estándar, podemos simular fácilmente una variable aleatoria estable para todos los valores admisibles de los parámetros , , y utilizando la siguiente propiedad. Si entonces ${\ Displaystyle \ alpha}$${\ Displaystyle c}$${\ Displaystyle \ beta}$${\ Displaystyle \ mu}$${\ Displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

${\ Displaystyle Y = {\ begin {cases} cX + \ mu & \ alpha \ neq 1 \\ cX + {\ frac {2} {\ pi}} \ beta c \ log c + \ mu & \ alpha = 1 \ end { casos}}}$

es . Para (y ) el método CMS se reduce a la conocida transformada de Box-Muller para generar variables aleatorias gaussianas . Se han propuesto muchos otros enfoques en la literatura, incluida la aplicación de las expansiones de las series Bergström y LePage, ver y, respectivamente. Sin embargo, el método CMS se considera el más rápido y el más preciso. ${\ Displaystyle S _ {\ alpha} (\ beta, c, \ mu)}$${\ Displaystyle \ alpha = 2}$${\ Displaystyle \ beta = 0}$

Aplicaciones

Las distribuciones estables deben su importancia tanto en la teoría como en la práctica a la generalización del teorema del límite central a las variables aleatorias sin momentos de segundo (y posiblemente de primer) orden y la auto-semejanza que las acompaña de la familia estable. Fue la aparente desviación de la normalidad junto con la demanda de un modelo auto-similar para los datos financieros (es decir, la forma de la distribución de los cambios anuales en el precio de los activos debería parecerse a la de los cambios de precios diarios o mensuales constituyentes) lo que llevó a Benoît Mandelbrot a proponer que los precios del algodón siguen una distribución estable alfa con α igual a 1,7. Las distribuciones de Lévy se encuentran con frecuencia en el análisis de comportamiento crítico y datos financieros.

También se encuentran en espectroscopia como una expresión general para una línea espectral ensanchada por presión cuasiestática .

La distribución de Lévy de los eventos de tiempo de espera de las erupciones solares (tiempo entre los eventos de las erupciones ) se demostró para las erupciones solares de rayos X duros de CGRO BATSE en diciembre de 2001. El análisis de la firma estadística de Lévy reveló que eran evidentes dos firmas de memoria diferentes; uno relacionado con el ciclo solar y el segundo cuyo origen parece estar asociado con una combinación de efectos localizados de la región activa solar.

Otros casos analíticos

Se conocen varios casos de distribuciones estables expresables analíticamente. Dejemos que la distribución estable se exprese para entonces sabemos: ${\ Displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

• La distribución de Cauchy está dada por${\ Displaystyle f (x; 1, 0, 1, 0).}$
• La distribución de Lévy viene dada por${\ displaystyle f (x; {\ tfrac {1} {2}}, 1,1,0).}$
• La distribución normal está dada por${\ Displaystyle f (x; 2,0,1,0).}$
• Sea una función de Lommel , entonces:${\ Displaystyle S _ {\ mu, \ nu} (z)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {3}}, 0,1,0 \ right) = \ Re \ left ({\ frac {2e ^ {- {\ frac {i \ pi} {4}}}} {3 {\ sqrt {3}} \ pi}} {\ frac {1} {\ sqrt {x ^ {3}}}} S_ {0, {\ frac {1} {3} }} \ left ({\ frac {2e ^ {\ frac {i \ pi} {4}}} {3 {\ sqrt {3}}}} {\ frac {1} {\ sqrt {x}}} \ bien bien)}$

• Dejemos y denotemos las integrales de Fresnel entonces:${\ Displaystyle S (x)}$${\ Displaystyle C (x)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {2}}, 0,1,0 \ right) = {\ frac {1} {\ sqrt {2 \ pi | x | ^ {3}} }} \ left (\ sin \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}} - S \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right] + \ cos \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}} - C \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right] \ right)}$

• Sea la función de Bessel modificada del segundo tipo entonces:${\ Displaystyle K_ {v} (x)}$

${\ Displaystyle f \ left (x; {\ tfrac {1} {3}}, 1,1,0 \ right) = {\ frac {1} {\ pi}} {\ frac {2 {\ sqrt {2 }}} {3 ^ {\ frac {7} {4}}}} {\ frac {1} {\ sqrt {x ^ {3}}}} K _ {\ frac {1} {3}} \ left ( {\ frac {4 {\ sqrt {2}}} {3 ^ {\ frac {9} {4}}}} {\ frac {1} {\ sqrt {x}}} \ right)}$

• Si denotan las funciones hipergeométricas, entonces:${\ Displaystyle {} _ {m} F_ {n}}$

${\ displaystyle {\ begin {alineado} f \ left (x; {\ tfrac {4} {3}}, 0,1,0 \ right) & = {\ frac {3 ^ {\ frac {5} {4 }}} {4 {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {7} {12}} \ right) \ Gamma \ left ({\ tfrac {11} { 12}} \ right)} {\ Gamma \ left ({\ tfrac {6} {12}} \ right) \ Gamma \ left ({\ tfrac {8} {12}} \ right)}} {} _ { 2} F_ {2} \ left ({\ tfrac {7} {12}}, {\ tfrac {11} {12}}; {\ tfrac {6} {12}}, {\ tfrac {8} {12 }}; {\ tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} \ right) - {\ frac {3 ^ {\ frac {11} {4}} x ^ {3 }} {4 ^ {3} {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {13} {12}} \ right) \ Gamma \ left ({\ tfrac { 17} {12}} \ right)} {\ Gamma \ left ({\ tfrac {18} {12}} \ right) \ Gamma \ left ({\ tfrac {15} {12}} \ right)}} { } _ {2} F_ {2} \ left ({\ tfrac {13} {12}}, {\ tfrac {17} {12}}; {\ tfrac {18} {12}}, {\ tfrac {15 } {12}}; {\ tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} \ right) \\ [6pt] f \ left (x; {\ tfrac {3} { 2}}, 0,1,0 \ right) & = {\ frac {\ Gamma \ left ({\ tfrac {5} {3}} \ right)} {\ pi}} {} _ {2} F_ { 3} \ left ({\ tfrac {5} {12}}, {\ tfrac {11} {12}}; {\ tfrac {1} {3}}, {\ tfrac {1} {2}}, { \ tfrac {5} {6}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ right) - {\ frac {x ^ {2}} {3 \ pi}} {} _ {3} F_ {4} \ l eft ({\ tfrac {3} {4}}, 1, {\ tfrac {5} {4}}; {\ tfrac {2} {3}}, {\ tfrac {5} {6}}, {\ tfrac {7} {6}}, {\ tfrac {4} {3}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ right) + {\ frac {7x ^ {4} \ Gamma \ left ({\ tfrac {4} {3}} \ right)} {3 ^ {4} \ pi ^ {2}}} {} _ {2} F_ {3} \ left ({\ tfrac {13} {12}}, {\ tfrac {19} {12}}; {\ tfrac {7} {6}}, {\ tfrac {3} {2}}, {\ tfrac {5} {3}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ right) \ end {alineado}}}$

siendo este último la distribución de Holtsmark .

• Sea una función de Whittaker , entonces:${\ Displaystyle W_ {k, \ mu} (z)}$

${\ Displaystyle {\ begin {alineado} f \ left (x; {\ tfrac {2} {3}}, 0,1,0 \ right) & = {\ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ tfrac {2} {27}} x ^ {- 2} \ right) W _ {- {\ frac {1} {2}}, { \ frac {1} {6}}} \ left ({\ tfrac {4} {27}} x ^ {- 2} \ right) \\ [8pt] f \ left (x; {\ tfrac {2} { 3}}, 1,1,0 \ right) & = {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left (- {\ tfrac {16} {27}} x ^ {- 2} \ right) W _ {{\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ tfrac {32} {27}} x ^ {- 2} \ right) \\ [8pt] f \ left (x; {\ tfrac {3} {2}}, 1,1,0 \ right) & = {\ begin {cases} {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x ^ {3} \ right) W _ {{\ frac { 1} {2}}, {\ frac {1} {6}}} \ left (- {\ frac {2} {27}} x ^ {3} \ right) & x <0 \\ {} \\ { \ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x ^ {3} \ right) W _ {- {\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ frac {2} {27}} x ^ {3} \ right) & x \ geq 0 \ end { casos}} \ end {alineado}}}$

Ver también

• Vuelo de Lévy
• Proceso Lévy
• Otras distribuciones de "ley de potencia"
  • Distribución de Pareto
  • Distribución Zeta
  • Distribución zipf
  • Distribución Zipf-Mandelbrot
• Distribuciones estables estables y moderadas con agrupamiento de volatilidad: aplicaciones financieras
• Distribución estable multivariante
• Distribución discreta-estable

Notas

• El programa STABLE para Windows está disponible en la página web estable de John Nolan: http://www.robustanalysis.com/public/stable.html . Calcula la densidad (pdf), la función de distribución acumulada (cdf) y los cuantiles para una distribución estable general, y realiza una estimación de máxima verosimilitud de parámetros estables y algunas técnicas de análisis de datos exploratorios para evaluar el ajuste de un conjunto de datos.
• libstable es una implementación de C para las funciones de distribución estable pdf, cdf, número aleatorio, cuantil y ajuste (junto con un paquete de replicación de referencia y un paquete R).
• R Package 'stabledist' por Diethelm Wuertz, Martin Maechler y miembros del equipo central de Rmetrics. Calcula densidad estable, probabilidad, cuantiles y números aleatorios. Actualizado el 12 de septiembre de 2016.

Referencias