Poliedro oblicuo regular - Regular skew polyhedron

En geometría , los poliedros sesgados regulares son generalizaciones al conjunto de poliedros regulares que incluyen la posibilidad de caras no planas o figuras de vértice . Coxeter observó figuras de vértices sesgados que crearon nuevos poliedros regulares de 4 dimensiones, y mucho más tarde Branko Grünbaum miró caras sesgadas regulares.

Los poliedros de sesgo regular infinito que abarcan 3 espacios o más se denominan apeiroedros de sesgo regular .

Historia

Según Coxeter , en 1926 John Flinders Petrie generalizó el concepto de polígonos sesgados regulares (polígonos no planos) a poliedros sesgados regulares .

Coxeter ofreció un símbolo de Schläfli modificado { l , m | n } para estas figuras, con { l , m } implicando la figura del vértice , m l -gones alrededor de un vértice y n -agujeros gonales. Sus figuras de vértice son polígonos sesgados , zigzagueando entre dos planos.

Los poliedros de sesgo regular, representados por { l , m | n } , sigue esta ecuación:

Un primer conjunto { l , m | n } , repite los cinco sólidos platónicos convexos y un sólido Kepler-Poinsot no convexo :

{ l , m | n } Caras Bordes Vértices pag Poliedro
Orden de simetría
{3,3 | 3} = {3,3} 4 6 4 0 Tetraedro 12
{3,4 | 4} = {3,4} 8 12 6 0 Octaedro 24
{4,3 | 4} = {4,3} 6 12 8 0 Cubo 24
{3,5 | 5} = {3,5} 20 30 12 0 Icosaedro 60
{5,3 | 5} = {5,3} 12 30 20 0 Dodecaedro 60
{5,5 | 3} = {5,5 / 2} 12 30 12 4 Gran dodecaedro 60

Poliedros oblicuos regulares finitos de 4 espacios

Proyecciones del plano A4 Coxeter
4-simplex t03.svg 4-simplex t12.svg
{4, 6 | 3} {6, 4 | 3}
Runcinated 5-celdas
(20 vértices, 60 aristas) 		Bitruncated 5 celdas
(30 vértices, 60 bordes)
Proyecciones del plano F4 Coxeter
24 celdas t03 F4.svg T12 F4.svg de 24 celdas
{4, 8 | 3} {8, 4 | 3}
24 celdas runcinadas
(144 vértices, 576 aristas) 		Bitruncated 24 celdas
(288 vértices, 576 aristas)
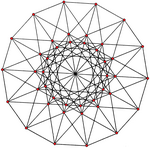
Poliedro complejo casi regular 42 vértices.png Poliedro complejo casi regular 46 vértices.png
{3,8 |, 4} = {3,8} 8 {4,6 |, 3} = {4,6} 6
42 vértices, 168 aristas 56 vértices, 168 aristas
Algunos de los poliedros oblicuos regulares de 4 dimensiones encajan dentro de la policora uniforme como se muestra en las 4 proyecciones superiores.

Coxeter también enumeró un conjunto más grande de poliedros regulares finitos en su artículo "poliedros sesgados regulares en tres y cuatro dimensiones, y sus análogos topológicos".

Al igual que los poliedros oblicuos infinitos representan superficies múltiples entre las celdas de los panales uniformes convexos , las formas finitas representan superficies múltiples dentro de las celdas de los 4 politopos uniformes .

Poliedros de la forma {2p, 2q | r} están relacionados con la simetría del grupo Coxeter de [(p, r, q, r)], que se reduce a la [r, p, r] lineal cuando q es 2. Coxeter da estas simetría como [[( p , r , q , r )] + ] que dice que es isomorfo a su grupo abstracto (2 p , 2 q | 2, r ). El panal relacionado tiene la simetría extendida [[( p , r , q , r )]].

{2p, 4 | r} está representado por la {2p} caras de la bitruncated {r, p, r} uniforme 4-politopo , y {4,2p | r} está representado por caras cuadradas de la runcinated {r, p , r}.

{4,4 | n} produce un n - n duoprisma , y específicamente {4,4 | 4} encaja dentro de un tesseract {4} x {4} .

El {4,4 | n} soluciones representan las caras cuadradas de los duoprismas, con las caras n-gonales como agujeros y representan un toro de Clifford , y una aproximación de un duocilindro
{4,4 | 6} tiene 36 caras cuadradas, vistas en proyección en perspectiva como cuadrados extraídos de un duoprisma 6,6 .
{4,4 | 4} tiene 16 caras cuadradas y existe como un subconjunto de caras en un tesseract .
Un anillo de 60 triángulos forma un poliedro sesgado regular dentro de un subconjunto de caras de una celda de 600 .
Incluso soluciones ordenadas
{l, m | norte} Caras Bordes Vértices pag Estructura Simetría Orden Policora uniforme relacionada
{4,4 | 3} 9 18 9 1 D 3 x D 3 [[3,2,3] + ] 9 3-3 duoprisma
{4,4 | 4} dieciséis 32 dieciséis 1 D 4 x D 4 [[4,2,4] + ] dieciséis 4-4 duoprisma o tesseract
{4,4 | 5} 25 50 25 1 D 5 x D 5 [[5,2,5] + ] 25 5-5 duoprisma
{4,4 | 6} 36 72 36 1 D 6 x D 6 [[6,2,6] + ] 36 6-6 duoprisma
{4,4 | norte} n 2 2n 2 n 2 1 D n xD n [[n, 2, n] + ] n 2 nn duoprisma
{4,6 | 3} 30 60 20 6 S5 [[3,3,3] + ] 60 5 celdas runcinadas
{6,4 | 3} 20 60 30 6 S5 [[3,3,3] + ] 60 Bitruncado de 5 celdas
{4,8 | 3} 288 576 144 73 [[3,4,3] + ] 576 24 celdas runcinadas
{8,4 | 3} 144 576 288 73 [[3,4,3] + ] 576 Bitruncado de 24 celdas
soluciones pentagrammicas
{l, m | norte} Caras Bordes Vértices pag Estructura Simetría Orden Policora uniforme relacionada
{4,5 | 5} 90 180 72 10 A6 [[5 / 2,5,5 / 2] + ] 360 120 celdas gran estrelladas runcinadas
{5,4 | 5} 72 180 90 10 A6 [[5 / 2,5,5 / 2] + ] 360 120 celdas grandes estrelladas bitruncadas
{l, m | norte} Caras Bordes Vértices pag Estructura Orden
{4,5 | 4} 40 80 32 5 ? 160
{5,4 | 4} 32 80 40 5 ? 160
{4,7 | 3} 42 84 24 10 LF (2,7) 168
{7,4 | 3} 24 84 42 10 LF (2,7) 168
{5,5 | 4} 72 180 72 19 A6 360
{6,7 | 3} 182 546 156 105 LF (2,13) 1092
{7,6 | 3} 156 546 182 105 LF (2,13) 1092
{7,7 | 3} 156 546 156 118 LF (2,13) 1092
{4,9 | 3} 612 1224 272 171 LF (2,17) 2448
{9,4 | 3} 272 1224 612 171 LF (2,17) 2448
{7,8 | 3} 1536 5376 1344 1249 ? 10752
{8,7 | 3} 1344 5376 1536 1249 ? 10752

Un conjunto final se basa en la forma ampliada adicional de Coxeter {q1, m | q2, q3 ...} o con q2 sin especificar: {l, m |, q}. Estos también se pueden representar como un mapa finito regular o { l , m } 2 q , y el grupo G l , m , q .

{ l , m |, q } o { l , m } 2 q Caras Bordes Vértices pag Estructura Orden Notas
{3,6 |, q } = {3,6} 2 q 2 q 2 3 q 2 q 2 1 G 3,6,2 q 2 q 2
{3,2 q |, 3} = {3,2 q } 6 2q 2 3q 2 3q ( q -1) * ( q -2) / 2 G 3,6,2 q 2 q 2
{3,7 |, 4} = {3,7} 8 56 84 24 3 LF (2,7) 168
{3,8 |, 4} = {3,8} 8 112 168 42 8 PGL (2,7) 336 Relacionado con poliedro complejo (1 1 1 1 4 ) 4 ,Nodo CDel 1.pngCDel 4split1.pngCDel branch.pngCDel label4.png
{4,6 |, 3} = {4,6} 6 84 168 56 15 PGL (2,7) 336 Relacionado con poliedro complejo (1 4 1 4 1 1 ) (3) ,Nodo CDel 1.pngCDel anti3split1-44.pngCDel branch.png
{3,7 |, 6} = {3,7} 12 364 546 156 14 LF (2,13) 1092
{3,7 |, 7} = {3,7} 14 364 546 156 14 LF (2,13) 1092
{3,8 |, 5} = {3,8} 10 720 1080 270 46 G 3,8,10 2160 Relacionado con poliedro complejo (1 1 1 1 4 ) 5 ,Nodo CDel 1.pngCDel 5split1.pngCDel branch.pngCDel label4.png
{3,10 |, 4} = {3,10} 8 720 1080 216 73 G 3,8,10 2160 Relacionado con poliedro complejo (1 1 1 1 5 ) 4 ,Nodo CDel 1.pngCDel 4split1.pngCDel branch.pngCDel label5.png
{4,6 |, 2} = {4,6} 4 12 24 8 3 S4 × S2 48
{5,6 |, 2} = {5,6} 4 24 60 20 9 A5 × S2 120
{3,11 |, 4} = {3,11} 8 2024 3036 552 231 LF (2,23) 6072
{3,7 |, 8} = {3,7} 16 3584 5376 1536 129 G 3,7,17 10752
{3,9 |, 5} = {3,9} 10 12180 18270 4060 1016 LF (2,29) × A3 36540

Mayores dimensiones

Los poliedros oblicuos regulares también se pueden construir en dimensiones superiores a 4 como incrustaciones en politopos regulares o panales. Por ejemplo, el icosaedro regular se puede incrustar en los vértices del 6-demicubo ; esto fue nombrado el icosaedro sesgado regular por HSM Coxeter . El dodecaedro se puede incrustar de manera similar en el 10-demicubo .

Ver también

Notas

Referencias

  • Peter McMullen, Poliedros regulares tetradimensionales , geometría discreta y computacional, septiembre de 2007, volumen 38, número 2, págs. 355–387
  • Coxeter , Regular Polytopes , Tercera edición, (1973), Edición Dover, ISBN  0-486-61480-8
  • Kaleidoscopes: Selected Writings of HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Documento 2) HSM Coxeter, "Las esponjas regulares o poliedros sesgados", Scripta Mathematica 6 (1939) 240-244.
    • (Documento 22) HSM Coxeter, Politopos regulares y semi regulares I , [Math. Zeit. 46 (1940) 380–407, MR 2,10]
    • (Documento 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559–591]
  • Coxeter , The Beauty of Geometry: Twelve Essays , Dover Publications, 1999, ISBN  0-486-40919-8 (Capítulo 5: Regular Skew Polyhedra en tres y cuatro dimensiones y sus análogos topológicos, Proceedings of the London Mathematics Society, Ser.2 , Vol.43, 1937.)
    • Coxeter, poliedros oblicuos regulares HSM en tres y cuatro dimensiones. Proc. London Math. Soc. 43, 33-62, 1937.
  • Garner, CWL Regular Skew Polyhedra en Hyperbolic Three-Space. Poder. J. Math. 19, 1179-1186, 1967.
  • E. Schulte, JM Wills On Coxeter's regular skew polyhedra , Discrete Mathematics, Volumen 60, junio-julio de 1986, páginas 253–262