Árbol de intervalo - Interval tree

En informática , un árbol de intervalos es una estructura de datos de árbol para contener intervalos . Específicamente, le permite a uno encontrar de manera eficiente todos los intervalos que se superponen con cualquier intervalo o punto dado. A menudo se usa para consultas de ventanas, por ejemplo, para encontrar todas las carreteras en un mapa computarizado dentro de una ventana rectangular, o para encontrar todos los elementos visibles dentro de una escena tridimensional. Una estructura de datos similar es el árbol de segmentos .

La solución trivial es visitar cada intervalo y probar si se cruza con el punto o intervalo dado, lo que requiere tiempo, donde está el número de intervalos en la colección. Dado que una consulta puede devolver todos los intervalos, por ejemplo, si la consulta es un intervalo grande que interseca todos los intervalos de la colección, esto es asintóticamente óptimo ; sin embargo, podemos hacerlo mejor si consideramos algoritmos sensibles a la salida , donde el tiempo de ejecución se expresa en términos del número de intervalos producidos por la consulta. Los árboles de intervalo tienen un tiempo de consulta de y un tiempo de creación inicial de , mientras que limitan el consumo de memoria a . Después de la creación, los árboles de intervalo pueden ser dinámicos, lo que permite la inserción y eliminación eficiente de un intervalo en el tiempo. Si los puntos finales de los intervalos están dentro de un rango de números enteros pequeños ( por ejemplo , en el rango ), existen estructuras de datos más rápidas y de hecho óptimas con tiempo de preprocesamiento y tiempo de consulta para informes de intervalos que contienen un punto de consulta dado (ver uno muy simple). ${\ Displaystyle O (n)}$ ${\ Displaystyle n}$ ${\ Displaystyle m}$ ${\ Displaystyle O (\ log n + m)}$ ${\ Displaystyle O (n \ log n)}$ ${\ Displaystyle O (n)}$ ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle [1, \ ldots, O (n)]}$ ${\ Displaystyle O (n)}$ ${\ Displaystyle O (1 + m)}$ ${\ Displaystyle m}$

Enfoque ingenuo

En un caso simple, los intervalos no se superponen y pueden insertarse en un árbol de búsqueda binario simple y consultarse en el tiempo. Sin embargo, con intervalos superpuestos arbitrariamente, no hay forma de comparar dos intervalos para la inserción en el árbol, ya que los ordenamientos ordenados por los puntos iniciales o finales pueden ser diferentes. Un enfoque ingenuo podría ser construir dos árboles paralelos, uno ordenado por el punto inicial y otro ordenado por el punto final de cada intervalo. Esto permite descartar la mitad de cada árbol a tiempo, pero los resultados deben fusionarse, lo que requiere tiempo. Esto nos da consultas , que no es mejor que la fuerza bruta. ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle O (n)}$ ${\ Displaystyle O (n + \ log n) = O (n)}$

Los árboles de intervalos resuelven este problema. Este artículo describe dos diseños alternativos para un árbol de intervalo, denominado árbol de intervalo centrado y árbol aumentado .

Árbol de intervalo centrado

Las consultas requieren tiempo, siendo el número total de intervalos y el número de resultados informados. La construcción requiere tiempo y el almacenamiento requiere espacio. ${\ Displaystyle O (\ log n + m)}$ ${\ Displaystyle n}$ ${\ Displaystyle m}$ ${\ Displaystyle O (n \ log n)}$ ${\ Displaystyle O (n)}$

Construcción

Dado un conjunto de intervalos en la recta numérica, queremos construir una estructura de datos para poder recuperar de manera eficiente todos los intervalos que se superponen a otro intervalo o punto. ${\ Displaystyle n}$

Comenzamos tomando el rango completo de todos los intervalos y dividiéndolo por la mitad en (en la práctica, se debe recolectar para mantener el árbol relativamente equilibrado). Esto da tres conjuntos de intervalos, los completamente a la izquierda de los que llamaremos , los completamente a la derecha de los que llamaremos y los superpuestos a los que llamaremos . ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {izquierda}}}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {derecha}}}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {center}}}$

Los intervalos en y se dividen recursivamente de la misma manera hasta que no queden intervalos. ${\ displaystyle S _ {\ textrm {izquierda}}}$ ${\ displaystyle S _ {\ textrm {derecha}}}$

Los intervalos que se superponen con el punto central se almacenan en una estructura de datos separada vinculada al nodo en el árbol de intervalos. Esta estructura de datos consta de dos listas, una que contiene todos los intervalos ordenados por sus puntos iniciales y otra que contiene todos los intervalos ordenados por sus puntos finales. ${\ displaystyle S _ {\ textrm {center}}}$

El resultado es un árbol binario en el que cada nodo almacena:

Un punto central
Un puntero a otro nodo que contiene todos los intervalos completamente a la izquierda del punto central
Un puntero a otro nodo que contiene todos los intervalos completamente a la derecha del punto central
Todos los intervalos que se superponen al punto central ordenados por su punto de inicio
Todos los intervalos que se superponen al punto central ordenados por su punto final

Intersección

Dada la estructura de datos construida anteriormente, recibimos consultas que consisten en rangos o puntos, y devolvemos todos los rangos del conjunto original superpuestos a esta entrada.

Con un punto

La tarea es encontrar todos los intervalos en el árbol que se superponen a un punto dado . El árbol se recorre con un algoritmo recursivo similar al que se usaría para atravesar un árbol binario tradicional, pero con lógica adicional para respaldar la búsqueda de los intervalos que se superponen al punto "central" en cada nodo. ${\ Displaystyle x}$

Para cada nodo del árbol, se compara con el punto medio utilizado en la construcción del nodo anterior. Si es menor que , se considera el conjunto de intervalos situado más a la izquierda`` . Si es mayor que , el conjunto de la derecha de intervalos, , se considera. ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {izquierda}}}$ ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {derecha}}}$

Todos los intervalos que comienzan antes deben superponerse si es menor que . De manera similar, la misma técnica también se aplica al verificar un intervalo dado. Si un determinado intervalo en extremos y e y es menor que , en todos los intervalos que comienzan antes y también debe solapar el intervalo dado.

{\ displaystyle S _ {\ textrm {center}}}

{\ Displaystyle x}

{\ Displaystyle x}

{\ Displaystyle x}

{\ displaystyle x _ {\ textrm {center}}}

{\ displaystyle x _ {\ textrm {center}}}

{\ displaystyle S _ {\ textrm {center}}}

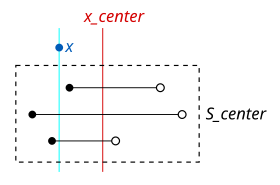
A medida que se procesa cada nodo a medida que atravesamos el árbol desde la raíz hasta la hoja, se procesan los rangos en él . Si es menor que , sabemos que todos los intervalos terminan después , o no podrían también solaparse . Por lo tanto, solo necesitamos encontrar los intervalos que comienzan antes . Podemos consultar las listas de los que ya se han construido. Dado que en este escenario solo nos interesan los comienzos de intervalo, podemos consultar la lista ordenada por comienzos. Suponga que encontramos el número más cercano no mayor que en esta lista. Todos los rangos desde el principio de la lista hasta el punto encontrado se superponen porque comienzan antes y terminan después (como sabemos porque se superponen, que es más grande que ). Por lo tanto, podemos simplemente comenzar a enumerar intervalos en la lista hasta que exceda el valor del punto de inicio . ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$

Del mismo modo, si es mayor que , sabemos que todos los intervalos en deben comenzar antes , por lo que encontramos los intervalos que terminan después de usar la lista ordenada por terminaciones de intervalo. ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle x}$ ${\ Displaystyle x}$

Si coincide exactamente , todos los intervalos en se pueden agregar a los resultados sin más procesamiento y se puede detener el recorrido del árbol. ${\ Displaystyle x}$ ${\ displaystyle x _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {center}}}$

Con un intervalo

Para que un intervalo de resultados se cruce con nuestro intervalo de consulta, debe cumplirse uno de los siguientes: ${\ Displaystyle r}$ ${\ Displaystyle q}$

el punto inicial y / o final de está en ; o ${\ Displaystyle r}$ ${\ Displaystyle q}$
${\ Displaystyle r}$ encierra completamente . ${\ Displaystyle q}$

Primero encontramos todos los intervalos con puntos de inicio y / o final en el interior usando un árbol construido por separado. En el caso unidimensional, podemos usar un árbol de búsqueda que contenga todos los puntos de inicio y finalización en el intervalo establecido, cada uno con un puntero a su intervalo correspondiente. Una búsqueda binaria en el tiempo para el inicio y el final de revela los puntos mínimos y máximos a considerar. Cada punto dentro de este rango hace referencia a un intervalo que se superpone y se agrega a la lista de resultados. Se debe tener cuidado para evitar duplicados, ya que un intervalo puede comenzar y terminar en el mismo . Esto se puede hacer usando una bandera binaria en cada intervalo para marcar si se ha agregado o no al conjunto de resultados. ${\ Displaystyle q}$ ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle q}$ ${\ Displaystyle q}$ ${\ Displaystyle q}$

Finalmente, debemos encontrar intervalos que encierren . Para encontrarlos, elegimos cualquier punto dentro y usamos el algoritmo anterior para encontrar todos los intervalos que se cruzan con ese punto (nuevamente, teniendo cuidado de eliminar los duplicados). ${\ Displaystyle q}$ ${\ Displaystyle q}$

Mayores dimensiones

La estructura de datos del árbol de intervalos se puede generalizar a una dimensión superior con tiempo y espacio de consulta y construcción idénticos . ${\ Displaystyle N}$ ${\ Displaystyle O (n \ log n)}$

Primero, se construye un árbol de rangos en dimensiones que permite la recuperación eficiente de todos los intervalos con puntos de inicio y fin dentro de la región de consulta . Una vez que se encuentran los rangos correspondientes, lo único que queda son aquellos rangos que encierran la región en alguna dimensión. Para encontrar estas superposiciones, se crean árboles de intervalo y se consulta un eje que se cruza para cada uno. Por ejemplo, en dos dimensiones, la parte inferior del cuadrado (o cualquier otra línea horizontal que se cruce ) se compararía con el árbol de intervalos construido para el eje horizontal. Asimismo, la izquierda (o cualquier otra línea vertical que se cruce ) se compararía con el árbol de intervalos construido en el eje vertical. ${\ Displaystyle N}$ ${\ Displaystyle R}$ ${\ Displaystyle N}$ ${\ Displaystyle R}$ ${\ Displaystyle R}$ ${\ Displaystyle R}$ ${\ Displaystyle R}$

Cada árbol de intervalo también necesita una adición para dimensiones más altas. En cada nodo que atravesamos en el árbol, se compara con para encontrar superposiciones. En lugar de dos listas ordenadas de puntos como se usó en el caso unidimensional, se construye un árbol de rangos. Esto permite la recuperación eficiente de todos los puntos en esa región de superposición . ${\ Displaystyle x}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ displaystyle S _ {\ textrm {center}}}$ ${\ Displaystyle R}$

Supresión

Si después de eliminar un intervalo del árbol, el nodo que contiene ese intervalo no contiene más intervalos, ese nodo puede eliminarse del árbol. Esto es más complejo que una operación normal de eliminación de árbol binario.

Un intervalo puede superponerse al punto central de varios nodos del árbol. Dado que cada nodo almacena los intervalos que lo superponen, con todos los intervalos completamente a la izquierda de su punto central en el subárbol izquierdo, de manera similar para el subárbol derecho, se deduce que cada intervalo se almacena en el nodo más cercano a la raíz del conjunto de nodos cuyo punto central se superpone.

Las operaciones de eliminación normales en un árbol binario (para el caso en el que el nodo que se elimina tiene dos hijos) implican promover un nodo más lejos de la hoja hasta la posición del nodo que se elimina (generalmente el hijo más a la izquierda del subárbol derecho, o el hijo más a la derecha del subárbol izquierdo).

Eliminar un nodo con dos hijos de un árbol de búsqueda binaria utilizando el predecesor en orden (nodo más a la derecha en el subárbol izquierdo, etiquetado como 6 ).

Como resultado de esta promoción, algunos nodos que estaban por encima del nodo promocionado se convertirán en sus descendientes; es necesario buscar en estos nodos intervalos que también se superpongan al nodo promovido y mover esos intervalos al nodo promovido. Como consecuencia, esto puede resultar en nuevos nodos vacíos, que deben ser eliminados, siguiendo el mismo algoritmo nuevamente.

Equilibrio

Los mismos problemas que afectan la eliminación también afectan las operaciones de rotación; la rotación debe preservar el invariante de que los nodos se almacenan lo más cerca posible de la raíz.

Árbol aumentado

Un árbol aumentado con un valor bajo como clave y un máximo alto como anotación adicional.

Por ejemplo, al probar si el intervalo dado [40, 60) se superpone a los intervalos en el árbol que se muestra arriba, vemos que no se superpone al intervalo [20, 36) en la raíz, pero dado que el valor bajo de la raíz (20) es menor que el valor alto buscado (60), debemos buscar el subárbol correcto. El máximo alto del subárbol izquierdo de 41 excede el valor bajo buscado (40), por lo que debemos buscar también en el subárbol izquierdo. Sin embargo, ambos descendientes del nodo [3, 41) tienen máximos máximos inferiores a 40, por lo que la búsqueda del subárbol izquierdo termina allí y no es necesario buscarlos.

Otra forma de representar intervalos se describe en Cormen et al. (2009 , Sección 14.3: Árboles de intervalo, págs. 348–354).

Tanto la inserción como la eliminación requieren tiempo, siendo el número total de intervalos en el árbol antes de la operación de inserción o eliminación. ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle n}$

Se puede construir un árbol aumentado a partir de un árbol ordenado simple, por ejemplo, un árbol de búsqueda binario o un árbol de búsqueda binario autoequilibrado , ordenados por los valores 'bajos' de los intervalos. Luego se agrega una anotación adicional a cada nodo, registrando el valor superior máximo entre todos los intervalos desde este nodo hacia abajo. Mantener este atributo implica actualizar todos los ancestros del nodo de abajo hacia arriba cada vez que se agrega o elimina un nodo. Esto solo toma O ( h ) pasos por adición o eliminación de nodo, donde h es la altura del nodo agregado o eliminado en el árbol. Si hay rotaciones de árbol durante la inserción y eliminación, es posible que los nodos afectados también deban actualizarse.

Ahora, se sabe que dos intervalos y se superponen solo cuando ambos y . Al buscar en los árboles nodos que se superponen con un intervalo determinado, puede omitir inmediatamente: ${\ Displaystyle A}$ ${\ Displaystyle B}$ ${\ displaystyle A _ {\ textrm {bajo}} \ leq B _ {\ textrm {alto}}}$ ${\ displaystyle A _ {\ textrm {alto}} \ geq B _ {\ textrm {bajo}}}$

todos los nodos a la derecha de los nodos cuyo valor bajo es más allá del final del intervalo dado.
todos los nodos que tienen su valor alto máximo por debajo del inicio del intervalo dado.

Consultas de membresía

Se puede obtener algo de rendimiento si el árbol evita recorridos innecesarios. Estos pueden ocurrir al agregar intervalos que ya existen o al eliminar intervalos que no existen.

Se puede definir un orden total en los intervalos ordenándolos primero por sus límites inferiores y luego por sus límites superiores. Luego, se puede realizar una verificación de membresía a tiempo, en comparación con el tiempo requerido para encontrar duplicados si los intervalos se superponen con el intervalo que se insertará o eliminará. Esta solución tiene la ventaja de no requerir estructuras adicionales. El cambio es estrictamente algorítmico. La desventaja es que las consultas de membresía llevan tiempo. ${\ Displaystyle O (\ log n)}$ ${\ Displaystyle O (k + \ log n)}$ ${\ Displaystyle k}$ ${\ Displaystyle O (\ log n)}$

Alternativamente, a la velocidad de la memoria, las consultas de membresía en el tiempo constante esperado se pueden implementar con una tabla hash, actualizada en sincronía con el árbol de intervalos. Esto puede no necesariamente duplicar el requerimiento total de memoria, si los intervalos se almacenan por referencia en lugar de por valor. ${\ Displaystyle O (n)}$

Ejemplo de Java: agregar un nuevo intervalo al árbol

La clave de cada nodo es el intervalo en sí, por lo tanto, los nodos se ordenan primero por valor bajo y finalmente por valor alto, y el valor de cada nodo es el punto final del intervalo:

 public void add(Interval i) {
     put(i, i.getEnd());
 }

Ejemplo de Java: búsqueda de un punto o un intervalo en el árbol

Para buscar un intervalo, uno camina por el árbol, usando la clave ( n.getKey() ) y el valor alto ( n.getValue() ) para omitir cualquier rama que no pueda superponerse a la consulta. El caso más simple es una consulta puntual:

 // Search for all intervals containing "p", starting with the
 // node "n" and adding matching intervals to the list "result"
 public void search(IntervalNode n, Point p, List<Interval> result) {
     // Don't search nodes that don't exist
     if (n == null)
         return;

     // If p is to the right of the rightmost point of any interval
     // in this node and all children, there won't be any matches.
     if (p.compareTo(n.getValue()) > 0)
         return;

     // Search left children
     search(n.getLeft(), p, result);

     // Check this node
     if (n.getKey().contains(p))
         result.add(n.getKey());

     // If p is to the left of the start of this interval,
     // then it can't be in any child to the right.
     if (p.compareTo(n.getKey().getStart()) < 0)
         return;

     // Otherwise, search right children
     search(n.getRight(), p, result);
 }

dónde

a.compareTo(b) devuelve un valor negativo si a <b

a.compareTo(b) devuelve cero si a = b

a.compareTo(b) devuelve un valor positivo si a> b

El código para buscar un intervalo es similar, excepto por la marca en el medio:

 // Check this node
 if (n.getKey().overlapsWith(i))
     result.add (n.getKey());

solapasCon () se define como:

 public boolean overlapsWith(Interval other) {
     return start.compareTo(other.getEnd()) <= 0 &&
            end.compareTo(other.getStart()) >= 0;
 }

Mayores dimensiones

Los árboles aumentados se pueden extender a dimensiones más altas ciclando a través de las dimensiones en cada nivel del árbol. Por ejemplo, para dos dimensiones, los niveles impares del árbol pueden contener rangos para la coordenada x , mientras que los niveles pares contienen rangos para la coordenada y . Este enfoque convierte efectivamente la estructura de datos de un árbol binario aumentado a un árbol kd aumentado , lo que complica significativamente los algoritmos de equilibrio para inserciones y eliminaciones.

Una solución más sencilla es utilizar árboles de intervalo anidados. Primero, cree un árbol usando los rangos para la coordenada y . Ahora, para cada nodo en el árbol, agregue otro árbol de intervalos en los rangos x , para todos los elementos cuyo rango y es el mismo que el rango y de ese nodo .

La ventaja de esta solución es que se puede ampliar a un número arbitrario de dimensiones utilizando la misma base de código.

Al principio, el costo adicional de los árboles anidados puede parecer prohibitivo, pero generalmente no es así. Al igual que con la solución no anidada anterior, se necesita un nodo por coordenada x , lo que produce el mismo número de nodos para ambas soluciones. La única sobrecarga adicional es la de las estructuras de árbol anidadas, una por intervalo vertical. Esta estructura suele tener un tamaño insignificante, y consta solo de un puntero al nodo raíz y posiblemente al número de nodos y la profundidad del árbol.

Árbol orientado medial o longitudinalmente

Un árbol orientado medial o longitudinalmente es similar a un árbol aumentado, pero simétrico, con el árbol de búsqueda binario ordenado por los puntos mediales de los intervalos. Hay un montón binario orientado al máximo en cada nodo, ordenado por la longitud del intervalo (o la mitad de la longitud). También almacenamos el valor mínimo y máximo posible del subárbol en cada nodo (de ahí la simetría).

Prueba de superposición

Usando sólo empezar y terminar los valores de dos intervalos , para , la prueba de solapamiento se puede realizar de la siguiente manera: ${\ Displaystyle \ left (a_ {i}, b_ {i} \ right)}$ ${\ Displaystyle i = 0,1}$

${\ Displaystyle a_ {0} <b_ {1}}$ y ${\ Displaystyle a_ {1}> b_ {0}}$

Esto se puede simplificar usando la suma y la diferencia:

${\ Displaystyle s_ {i} = a_ {i} + b_ {i}}$

${\ Displaystyle d_ {i} = b_ {i} -a_ {i}}$

Lo que reduce la prueba de superposición a:

${\ Displaystyle \ left | s_ {1} -s_ {0} \ right | <d_ {0} + d_ {1}}$

Agregar intervalo

Agregar nuevos intervalos al árbol es lo mismo que para un árbol de búsqueda binaria usando el valor medial como clave. Pasamos al montón binario asociado con el nodo y actualizamos los valores mínimos y máximos posibles asociados con todos los nodos superiores. ${\ Displaystyle d_ {i}}$

Buscando todos los intervalos superpuestos

Usemos para el intervalo de consulta y para la clave de un nodo (en comparación con de intervalos) ${\ Displaystyle a_ {q}, b_ {q}, m_ {q}, d_ {q}}$ ${\ Displaystyle M_ {n}}$ ${\ Displaystyle m_ {i}}$

Comenzando con el nodo raíz, en cada nodo, primero verificamos si es posible que nuestro intervalo de consulta se superponga con el subárbol del nodo utilizando valores mínimos y máximos de nodo (si no es así, no continuamos para este nodo).

Luego calculamos los intervalos dentro de este nodo (no sus hijos) para superponerse con el intervalo de consulta (sabiendo ): ${\ Displaystyle \ min \ left \ {d_ {i} \ right \}}$ ${\ Displaystyle m_ {i} = M_ {n}}$

${\ Displaystyle \ min \ left \ {d_ {i} \ right \} = \ left | m_ {q} -M_ {n} \ right | -d_ {q}}$

y realizar una consulta en su montón binario para el mayor que ${\ Displaystyle d_ {i}}$ ${\ Displaystyle \ min \ left \ {d_ {i} \ right \}}$

Luego pasamos por los hijos derecho e izquierdo del nodo, haciendo lo mismo.

En el peor de los casos, tenemos que escanear todos los nodos del árbol de búsqueda binaria, pero dado que la consulta del montón binario es óptima, esto es aceptable (un problema bidimensional no puede ser óptimo en ambas dimensiones)

Se espera que este algoritmo sea más rápido que un árbol de intervalo tradicional (árbol aumentado) para operaciones de búsqueda. Agregar elementos es un poco más lento en la práctica, aunque el orden de crecimiento es el mismo.

Referencias

^ https://personal.us.es/almar/cg/08windowing.pdf
↑ ^a ^b Jens M. Schmidt . Problemas de apuñalamiento a intervalos en rangos de enteros pequeños . DOI . ISAAC'09, 2009
^ Consultas de rango # Operadores de semigrupo

Mark de Berg , Marc van Kreveld , Mark Overmars y Otfried Schwarzkopf . Geometría computacional , segunda edición revisada. Springer-Verlag 2000. Sección 10.1: Árboles de intervalo, págs. 212-217.
Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2009), Introducción a los algoritmos (3.a ed.), MIT Press y McGraw-Hill, ISBN 978-0-262-03384-8
Franco P. Preparata y Michael Ian Shamos . Geometría computacional: una introducción . Springer-Verlag, 1985

enlaces externos

CGAL: la biblioteca de algoritmos de geometría computacional en C ++ contiene una implementación robusta de árboles de rango
Boost.Icl ofrece implementaciones en C ++ de mapas y conjuntos de intervalos.
IntervalTree (Python) : un árbol de intervalos centrado con equilibrio AVL, compatible con intervalos etiquetados
Árbol de intervalos (C #) : un árbol de intervalos aumentado, con equilibrio AVL
Árbol de intervalos (Ruby) : un árbol de intervalos centrado, inmutable, compatible con intervalos etiquetados
IntervalTree (Java) : un árbol de intervalo aumentado, con equilibrio AVL, superposición de soporte, búsqueda, interfaz de colección, intervalos asociados a ID

[1] ttps://personal.us.es/almar/cg/08windowing.pdf

[Schmidt2009-2] Jens M. Schmidt . Problemas de apuñalamiento a intervalos en rangos de enteros pequeños . DOI . ISAAC'09, 2009

[3] Consultas de rango # Operadores de semigrupo

Languages

In other projects

Árbol de intervalo - Interval tree

Contenido

Enfoque ingenuo

Árbol de intervalo centrado

Construcción

Intersección

Con un punto

Con un intervalo

Mayores dimensiones

Supresión

Equilibrio

Árbol aumentado

Consultas de membresía

Ejemplo de Java: agregar un nuevo intervalo al árbol

Ejemplo de Java: búsqueda de un punto o un intervalo en el árbol

Mayores dimensiones

Árbol orientado medial o longitudinalmente

Prueba de superposición

Agregar intervalo

Buscando todos los intervalos superpuestos

Referencias

enlaces externos