Árbol de búsqueda binaria - Binary search tree

Árbol de búsqueda binaria
Árbol de búsqueda binaria
Escribe	árbol
Inventado	1960
Inventado por	PF Windley, AD Booth , AJT Colin y TN Hibbard
Complejidad del tiempo en notación O grande
Algoritmo
Algoritmo
Espacio
Buscar
Insertar
Borrar

Un árbol de búsqueda binaria de tamaño 9 y profundidad 3, con 8 en la raíz. Las hojas no se dibujan.

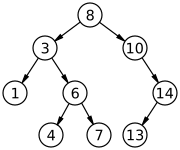
En ciencias de la computación , un árbol binario de búsqueda ( BST ), también llamado ordenado o ordenados árbol binario , es un arraigado árbol binario estructura de datos cuyo interior nodos cada tienda una mayor tecla que no todas las claves en subárbol izquierdo del nodo y menos que los de su subárbol derecho. Un árbol binario es un tipo de estructura de datos para almacenar datos como números de forma organizada. Los árboles de búsqueda binaria permiten la búsqueda binaria para una rápida búsqueda, adición y eliminación de elementos de datos, y se pueden utilizar para implementar conjuntos dinámicos y tablas de búsqueda . El orden de los nodos en un medio BST que cada comparación se salta sobre medio del árbol restante, por lo que toda la búsqueda lleva tiempo proporcional a la logaritmo binario del número de elementos almacenados en el árbol. Esto es mucho mejor que el tiempo lineal requerido para encontrar elementos por clave en una matriz (sin clasificar), pero más lento que las operaciones correspondientes en tablas hash . Se han estudiado varias variantes del árbol de búsqueda binaria.

Definición

Un árbol de búsqueda binaria es un árbol binario enraizado , cuyos nodos internos almacenan cada uno una clave (y, opcionalmente, un valor asociado), y cada uno tiene dos subárboles distinguidos, comúnmente denominados izquierda y derecha . El árbol además satisface la propiedad de búsqueda binaria : la clave en cada nodo es mayor o igual que cualquier clave almacenada en el subárbol izquierdo, y menor o igual que cualquier clave almacenada en el subárbol derecho. Las hojas (nodos finales) del árbol no contienen clave y no tienen estructura que las distinga entre sí.

A menudo, la información representada por cada nodo es un registro en lugar de un solo elemento de datos. Sin embargo, para fines de secuenciación, los nodos se comparan según sus claves en lugar de cualquier parte de sus registros asociados. La principal ventaja de los árboles de búsqueda binaria sobre otras estructuras de datos es que los algoritmos de clasificación relacionados y los algoritmos de búsqueda , como el recorrido por orden, pueden ser muy eficientes.

Árboles binarios de búsqueda son un elemento fundamental estructura de datos utilizada para construir estructuras de datos más abstractos tales como conjuntos , conjuntos múltiples y matrices asociativas .

Al insertar o buscar un elemento en un árbol de búsqueda binario, la clave de cada nodo visitado debe compararse con la clave del elemento a insertar o encontrar.
La forma del árbol de búsqueda binaria depende completamente del orden de inserciones y eliminaciones y puede volverse degenerado.
Después de una larga secuencia entremezclada de inserción y eliminación aleatoria, la altura esperada del árbol se acerca a la raíz cuadrada del número de claves, $\sqrt n$ , que crece mucho más rápido que $log n$ .
Se han realizado muchas investigaciones para evitar la degeneración del árbol, lo que resulta en la complejidad del tiempo del peor de los casos de $O (n)$ (para obtener más detalles, consulte la sección Tipos ).

Relación de pedido

La búsqueda binaria requiere una relación de orden mediante la cual cada elemento (artículo) se puede comparar con cualquier otro elemento en el sentido de un preorden total . La parte del elemento que efectivamente tiene lugar en la comparación se llama clave . Ya sean duplicados, i. mi. diferentes elementos con la misma clave, se permitirán en el árbol o no, no depende de la relación de orden, sino del conjunto subyacente, es decir: solo de la aplicación. Para una función de búsqueda que admita y maneje duplicados en un árbol, consulte la sección Búsqueda con duplicados permitidos .

En el contexto de los árboles de búsqueda binarios, un preorden total se realiza de la forma más flexible mediante una subrutina de comparación de tres vías .

Operaciones

Los árboles de búsqueda binarios admiten tres operaciones principales: búsqueda (comprobar si hay una clave), inserción de un elemento y eliminación de un elemento. Los dos últimos posiblemente cambian el árbol, mientras que el primero es una operación de navegación y de solo lectura. Otras operaciones de solo lectura son el cruce, la verificación, etc.

buscando

La búsqueda en un árbol de búsqueda binaria de una clave específica se puede programar de forma recursiva o iterativa .

Comenzamos examinando el nodo raíz . Si el árbol es nulo , la clave que estamos buscando no existe en el árbol. De lo contrario, si la clave es igual a la de la raíz, la búsqueda es exitosa y devolvemos el nodo. Si la clave es menor que la de la raíz, buscamos en el subárbol izquierdo. Del mismo modo, si la clave es mayor que la de la raíz, buscamos el subárbol derecho. Este proceso se repite hasta que se encuentra la clave o el subárbol restante es nulo . Si la clave buscada no se encuentra después de alcanzar un subárbol nulo , entonces la clave no está presente en el árbol. Esto se expresa fácilmente como un algoritmo recursivo (implementado en Python ):

def search_recursively(key, node):
    if node is None or key == node.key:
        return node
    if key < node.key:
        return search_recursively(key, node.left)
    return search_recursively(key, node.right)

El mismo algoritmo se puede implementar de forma iterativa:

def search_iteratively(key, node):
    while node is not None and node.key != key:
        if key < node.key:
            node = node.left
        else:
            node = node.right
    return node

La siguiente versión interactiva de la función de búsqueda no usa punteros principales en la estructura de datos del nodo, sino que usa una pila para mantener los punteros a los ancestros. Esta pila está incrustada en una estructura más grande, llamada traverser.

struct TreeNode {
  struct TreeNode *child[2];
  int key;
  int value;
} Node;

#define LEFT  0
#define RIGHT 1
#define left  child[LEFT]
#define right child[RIGHT]

#define MAXheight 1024 // BST is possibly unbalanced

struct traverser {
  Node*  nod1;  // current position (NULL,
                //   if nod1->key ahead or behind all nodes of bst)
  int    dir;   // ∈ {LEFT,FOUND,RIGHT}, i.e.
                // == LEFT  <==> position at < nod1
                // == FOUND <==> position at   nod1
                // == RIGHT <==> position at > nod1
  Node** parent = &ancestors[0]; // -> parent of nod1 or NULL if root
  // ancestors[0] == trav->bst->root, if tree not empty.
  Node** limit  = &ancestors[MAXheight]; // -> utmost entry
  BST*   bst;   // -> BST to which this traverser belongs
  Node*  ancestors[MAXheight-1];
};

// search Iteratively with Traverser:
int searchIT (struct traverser* trav, int key) {
  assert (trav != NULL && trav->bst != NULL);
  trav->parent = &(trav->ancestors[-1]);
  dir = LEFT; // in case trav->bst (and while-loop) is empty
  node = trav->bst->root;
  while (node != NULL) {
    if (key == node->key) { // key is in the BST
      trav->node = node; // onto trav
      trav->dir = FOUND;
      // 2 == FOUND: key == node->key
      return node;
    }
    if (key < node->key) dir = LEFT;
    else dir = RIGHT;
    if (++(trav->parent) >= limit) { // stack overflow
      fprintf (stderr, "tree too deep\n");
      exit (EXIT_FAILURE);
    }
    *(trav->parent) = node; // onto stack
    node = node->child[dir];
  }; // end of while-loop
  // *(trav->parent) is the node of closest fit
  trav->dir = dir;
  // 0 == LEFT:  key < (*(trav->parent))->key
  // 1 == RIGHT: key > (*(trav->parent))->key
  return NULL;
}

Estos tres ejemplos no admiten duplicados, es decir, consideran el árbol como totalmente ordenado.

Se puede notar que el algoritmo recursivo es recursivo de cola . En un lenguaje que admita la optimización de llamadas de cola, los ejemplos recursivos e iterativos se compilarán en programas equivalentes.

Debido a que en el peor de los casos este algoritmo debe buscar desde la raíz del árbol hasta la hoja más alejada de la raíz, la operación de búsqueda lleva un tiempo proporcional a la altura del árbol (consulte la terminología del árbol ). En promedio, los árboles de búsqueda binaria con claves de $nodos$ tienen una altura de $O (log | Nodes |)$ . Sin embargo, en el peor de los casos, los árboles de búsqueda binaria pueden tener una altura de $O (| Nodos |)$ , cuando el árbol desequilibrado se asemeja a una lista vinculada ( árbol degenerado ).

Se permite la búsqueda con duplicados

Si la relación de orden es solo un preorden total, una extensión razonable de la funcionalidad es la siguiente: también en caso de igualdad buscar hasta las hojas. De este modo, permite especificar (o cablear) una dirección, donde insertar un duplicado, ya sea a la derecha o izquierda de todos los duplicados en el árbol hasta el momento. Si la dirección está cableada, ambas opciones, derecha e izquierda, admiten una pila con insertar duplicado como operación de inserción y eliminar como operación emergente.

def search_duplicatesAllowed(key, node):
    new_node = node
    while new_node != None:
        current_node = new_node
        if key < current_node.key:
            dir = 0  # LEFT
        else:  # key >= current_node.key:
            dir = 1  # RIGHT
        new_node = current_node.child[dir]
    return (dir, current_node)

Un tipo de árbol binario equipado con dicha función de búsqueda se vuelve estable .

El recorrido

Una vez que se ha creado el árbol de búsqueda binaria, sus elementos pueden ser recuperados a finde por recursiva atravesar el subárbol izquierdo del nodo raíz, el acceso al propio nodo, entonces la exploración recursiva el subárbol derecho del nodo, continuando este patrón con cada nodo en el árbol ya que se accede de forma recursiva. Al igual que con todos los árboles binarios, se puede realizar un recorrido previo al pedido o un recorrido posterior al pedido , pero es probable que ninguno de ellos sea útil para los árboles de búsqueda binarios . Un recorrido en orden de un árbol de búsqueda binario siempre dará como resultado una lista ordenada de elementos de nodo (números, cadenas u otros elementos comparables).

El código para el recorrido en orden en Python se proporciona a continuación. Llamará a la devolución de llamada (alguna función que el programador desee llamar en el valor del nodo, como imprimir en la pantalla) para cada nodo en el árbol.

def inorder_traversal(node, callback):
    if node == None:
        return
    inorder_traversal(node.leftChild, callback)
    callback(node.value)
    inorder_traversal(node.rightChild, callback)

El código para el recorrido (recursivo) en orden en C se proporciona a continuación. En este caso se utilizará printfpara imprimir el valor entero del nodo en la pantalla.

void inorder_traversal(Node *node) {
  if (node == NULL) return;
  inorder_traversal(node->left);
  printf("%i%i ,", node->key, node->value);
  inorder_traversal(node->right);
}

Cada forma de primer recorrido de profundidad de árbol binario requiere $2 \times (n -1) \in O (n)$ tiempo, ya que visita cada arco exactamente dos veces (una vez hacia abajo, una vez hacia arriba) mientras visita cada nodo. Este algoritmo también es $O (n)$ , por lo que es asintóticamente óptimo .

El recorrido también se puede implementar de forma iterativa . Para ciertas aplicaciones, por ejemplo, búsqueda igual mayor, búsqueda aproximada, una operación paraEl recorrido de un solo paso (iterativo) puede ser muy útil. Esto, por supuesto, se implementa sin la construcción de devolución de llamada.

Avanzando al nodo anterior o siguiente

Esta función es útil, por ejemplo, en los casos en los que la ubicación del elemento que se busca no se conoce con suficiente exactitud. Después de haber buscado un punto de partida, la búsqueda puede continuar de forma secuencial.

Es posible que el nodo con el que se debe iniciar se haya encontrado en la BST mediante una función de búsqueda. En el siguiente ejemplo, que no usa punteros principales, la pila de punteros a los ancestros se ha construido, por ejemplo, mediante una searchITfunción con resultado exitoso.

La función inorderNext devuelve un finde vecino de los encontrados node, ya sea el inorder- suc cesador (para dir=RIGHT) o la inorder- prede cesador (para dir=LEFT), y la actualización stack, por lo que el árbol de búsqueda binaria puede ser atravesada secuencialmente finde y buscó en la dirección dada dirmás adelante.

/* Returns the next or previous data item in inorder within the tree being traversed with trav, or if there are no more data items returns NULL.
In the former case inorderNext() may be called again to retrieve the second next item. */
Node* inorderNext (struct traverser* trav, dir) {
  assert (trav != NULL);
  assert (trav->dir == FOUND);
  assert (dir == LEFT || dir == RIGHT);

  newnode = trav->node->child[dir];
  if (newnode != NULL) {
// Part A: node has a dir-child.
    do {
      node = newnode;
      if (++(trav->parent) > limit) { // stack overflow
        fprintf (stderr, "tree too deep\n");
        exit (EXIT_FAILURE);
      }
      *(trav->parent) = node; // onto stack
      newnode = node->child[1-dir]
    } until (newnode == NULL);
    return node;
  }
// Part B: node does not have a dir-child.
  do {
    if (--(trav->parent) < &(trav->ancestors[0])) // stack is empty
      return NULL;
    oldnode = node;
    node = *(trav->parent); // parent of oldnode
  } until (oldnode != node->child[dir]);
  // now: oldnode == node->child[1-dir], i.e.
  //      node is ancestor (and predecessor for dir==LEFT resp.
  //      successor for dir==RIGHT) of the original trav->node.
  return node;
}

Tenga en cuenta que la función no utiliza teclas, lo que significa que los arcos del árbol de búsqueda binaria registran completamente la estructura secuencial. Para recorridos sin cambio de dirección, la complejidad promedio ( amortizada ) se debe a que un recorrido completo toma pasos para un BST de tamaño 1 paso para arco hacia arriba y 1 para arco hacia abajo. La complejidad del peor de los casos es con la altura del árbol. ${\ Displaystyle {\ mathcal {O}} (1),}$ ${\ Displaystyle 2n-2}$ ${\ Displaystyle n,}$ ${\ Displaystyle {\ mathcal {O}} (h)}$ ${\ Displaystyle h}$

La implementación requiere un espacio de pila proporcional a la altura del árbol.

Verificación

A veces ya tenemos un árbol binario y necesitamos determinar si es un BST. Este problema tiene una solución recursiva simple.

La propiedad BST (cada nodo del subárbol derecho debe ser más grande que el nodo actual y cada nodo del subárbol izquierdo debe ser más pequeño que el nodo actual) es la clave para determinar si un árbol es un BST o no. El algoritmo codicioso —simplemente atraviesa el árbol, en cada nodo verifica si el nodo contiene un valor mayor que el valor del hijo izquierdo y menor que el valor del hijo derecho— no funciona en todos los casos. Considere el siguiente árbol:

En el árbol de arriba, cada nodo cumple la condición de que el nodo contiene un valor mayor que su hijo izquierdo y más pequeño que su hijo derecho, y sin embargo no es un BST: el valor 5 está en el subárbol derecho del nodo que contiene 20 , una violación de la propiedad BST.

En lugar de tomar una decisión basada únicamente en los valores de un nodo y sus hijos, también necesitamos que la información fluya desde el padre. En el caso del árbol anterior, si pudiéramos recordar sobre el nodo que contiene el valor 20, veríamos que el nodo con el valor 5 está violando el contrato de propiedad BST.

Entonces, la condición que debemos verificar en cada nodo es:

si el nodo es el hijo izquierdo de su padre, entonces debe ser más pequeño (o igual) que el padre y debe pasar el valor de su padre a su subárbol derecho para asegurarse de que ninguno de los nodos en ese subárbol sea mayor que el padre
si el nodo es el hijo derecho de su padre, entonces debe ser más grande que el padre y debe pasar el valor de su padre al subárbol izquierdo para asegurarse de que ninguno de los nodos en ese subárbol sea menor que el padre.

Una solución recursiva en C ++ puede explicar esto con más detalle:

struct TreeNode {
    int key;
    int value;
    struct TreeNode *left;
    struct TreeNode *right;
};

bool isBST(struct TreeNode *node, int minKey, int maxKey) {
    if (node == NULL) return true;
    if (node->key < minKey || node->key > maxKey) return false;
    
    return isBST(node->left, minKey, node->key−1) && isBST(node->right, node->key+1, maxKey);
}

node->key+1y node->key−1están hechos para permitir solo elementos distintos en BST.

Si queremos que también estén presentes los mismos elementos, solo podemos usarlos node->keyen ambos lugares.

La llamada inicial a esta función puede ser algo como esto:

if (isBST(root, INT_MIN, INT_MAX)) {
    puts("This is a BST.");
} else {
    puts("This is NOT a BST!");
}

Básicamente, seguimos creando un rango válido (comenzando desde [MIN_VALUE, MAX_VALUE]) y seguimos reduciéndolo para cada nodo a medida que bajamos de forma recursiva.

Como se señaló en la sección #Traversal , un recorrido en orden de un árbol de búsqueda binario devuelve los nodos ordenados. Por lo tanto, solo necesitamos mantener el último nodo visitado mientras atravesamos el árbol y verificar si su clave es más pequeña (o más pequeña / igual, si se permiten duplicados en el árbol) en comparación con la clave actual.

Inserción

La inserción comienza como comenzaría una búsqueda; si la clave no es igual a la de la raíz, buscamos los subárboles izquierdo o derecho como antes. Eventualmente, llegaremos a un nodo externo y agregaremos el nuevo par clave-valor (aquí codificado como un registro 'newNode') como su hijo derecho o izquierdo, dependiendo de la clave del nodo. En otras palabras, examinamos la raíz e insertamos recursivamente el nuevo nodo en el subárbol izquierdo si su clave es menor que la de la raíz, o el subárbol derecho si su clave es mayor o igual que la raíz.

Así es como se puede realizar una inserción típica de árbol de búsqueda binaria en un árbol binario en C ++ :

void insert(Node*& root, int key, int value) {
  if (!root) 
    root = new Node(key, value);
  else if (key == root->key)
    root->value = value;
  else if (key < root->key)
    insert(root->left, key, value);
  else  // key > root->key
    insert(root->right, key, value);
}

Alternativamente, se podría implementar una versión no recursiva en C de esta manera. El uso de un puntero a puntero para realizar un seguimiento de dónde venimos permite que el código evite la verificación explícita y el manejo del caso en el que necesita insertar un nodo en la raíz del árbol:

void insert(Node** root, int key, int value) {
  Node **walk = root;
  while (*walk) { 
    int curkey = (*walk)->key;
    if (curkey == key) {
      (*walk)->value = value;
      return;
    }
    if (key > curkey) 
      walk = &(*walk)->right;
    else 
      walk = &(*walk)->left;
  }
  *walk = new Node(key, value);
}

En el siguiente ejemplo, que no utiliza punteros principales, la pila de punteros a los ancestros se ha construido, por ejemplo, mediante una searchITfunción con la clave de resultado node->keynot FOUND.

// insert after search Iteratively with Traverser:
void insertIT(struct traverser* trav,Node* node) {
  assert (trav != NULL);
  assert (trav->node != NULL);
  assert (trav->dir == LEFT || trav->dir == RIGHT);
  assert (node != NULL);
  trav->node->child[trav->dir] = node;
  if (++(trav->parent) > limit) { // stack overflow
    fprintf (stderr, "tree too deep\n");
    exit (EXIT_FAILURE);
  }
  *(trav->parent) = node; // onto stack
}

La variante de procedimiento destructiva anterior modifica el árbol en su lugar. Solo usa espacio de pila constante (y la versión iterativa también usa espacio de pila constante), pero la versión anterior del árbol se pierde. Alternativamente, como en el siguiente ejemplo de Python , podemos reconstruir todos los ancestros del nodo insertado; cualquier referencia a la raíz del árbol original sigue siendo válida, lo que hace que el árbol sea una estructura de datos persistente :

def binary_tree_insert(node, key, value):
    if node == None:
        return NodeTree(None, key, value, None)
    if key == node.key:
        return NodeTree(node.left, key, value, node.right)
    if key < node.key:
        return NodeTree(binary_tree_insert(node.left, key, value), node.key, node.value, node.right)
    return NodeTree(node.left, node.key, node.value, binary_tree_insert(node.right, key, value))

La parte que se reconstruye usa espacio $O (log n)$ en el caso promedio y $O (n)$ en el peor de los casos.

En cualquier versión, esta operación requiere un tiempo proporcional a la altura del árbol en el peor de los casos, que es $O (log n)$ tiempo en el caso promedio sobre todos los árboles, pero $O (n)$ tiempo en el peor de los casos.

Otra forma de explicar la inserción es que para insertar un nuevo nodo en el árbol, primero se compara su clave con la de la raíz. Si su clave es menor que la de la raíz, se compara con la clave del hijo izquierdo de la raíz. Si su clave es mayor, se compara con el hijo derecho de la raíz. Este proceso continúa, hasta que el nuevo nodo se compara con un nodo hoja, y luego se agrega como hijo derecho o izquierdo de este nodo, dependiendo de su clave: si la clave es menor que la clave de la hoja, entonces se inserta como la de la hoja. hijo izquierdo, de lo contrario como hijo derecho de la hoja.

Hay otras formas de insertar nodos en un árbol binario, pero esta es la única forma de insertar nodos en las hojas y al mismo tiempo preservar la estructura BST.

Supresión

Al eliminar un nodo de un árbol de búsqueda binario , es obligatorio mantener la secuencia en orden de los nodos. Hay muchas posibilidades para hacer esto. Sin embargo, el siguiente método que ha sido propuesto por T. Hibbard en 1962 garantiza que las alturas de los subárboles sujetos se cambian como máximo en uno. Hay tres casos posibles a considerar:

Eliminar un nodo sin hijos: simplemente elimine el nodo del árbol.
Eliminación de un nodo con un hijo: elimine el nodo y reemplácelo con su hijo.
Eliminación de un nodo D con dos hijos: elija el predecesor en orden de D o el sucesor en orden E (ver figura). En lugar de eliminar D , sobrescriba su clave y valor con E 's. Si E no tiene un hijo, elimine E de su padre anterior G ; Si E tiene un niño F , es un hijo derecho, por lo que es para reemplazar E a G .

Eliminar un nodo D con dos hijos de un árbol de búsqueda binaria. Primero se identifica el nodo más a la izquierda del subárbol derecho, el sucesor del orden E. Su valor se copia en el nodo D que se está eliminando. El sucesor en orden se puede eliminar fácilmente porque tiene como máximo un hijo (que en el caso general desequilibrado puede ser un subárbol).
El mismo método funciona simétricamente usando el predecesor C en orden .

En todos los casos, cuando D sea la raíz, vuelva a hacer que el nodo de reemplazo sea la raíz.

Los nodos con dos hijos (caso 3) son más difíciles de eliminar (ver figura). El sucesor en orden de un nodo D es el hijo más a la izquierda de su subárbol derecho, digamos E , y el predecesor en orden de un nodo es el hijo más a la derecha del subárbol izquierdo, dice C. En cualquier caso, tal nodo E o C no tendrá un resp izquierdo. hijo correcto, por lo que se puede eliminar de acuerdo con uno de los dos casos más simples 1 o 2 anteriores.

El uso constante del sucesor inorder o del predecesor inorder para cada instancia del caso de dos hijos puede conducir a un árbol desequilibrado , por lo que algunas implementaciones seleccionan uno u otro en momentos diferentes.

Análisis en tiempo de ejecución: aunque esta operación no siempre atraviesa el árbol hasta una hoja, siempre es una posibilidad; por tanto, en el peor de los casos, requiere un tiempo proporcional a la altura del árbol. No requiere más, incluso cuando el nodo tiene dos hijos, ya que sigue un solo camino y no visita ningún nodo dos veces.

def find_min(self):
    """Get minimum node in a subtree."""
    current_node = self
    while current_node.left_child:
        current_node = current_node.left_child
    return current_node

def replace_node_in_parent(self, new_value=None) -> None:
    if self.parent:
        if self == self.parent.left_child:
            self.parent.left_child = new_value
        else:
            self.parent.right_child = new_value
    if new_value:
        new_value.parent = self.parent

def binary_tree_delete(self, key) -> None:
    if key < self.key:
        self.left_child.binary_tree_delete(key)
        return
    if key > self.key:
        self.right_child.binary_tree_delete(key)
        return
    # Delete the key here
    if self.left_child and self.right_child:  # If both children are present
        successor = self.right_child.find_min()
        self.key = successor.key
        successor.binary_tree_delete(successor.key)
    elif self.left_child:  # If the node has only a *left* child
        self.replace_node_in_parent(self.left_child)
    elif self.right_child:  # If the node has only a *right* child
        self.replace_node_in_parent(self.right_child)
    else:
        self.replace_node_in_parent(None)  # This node has no children

Algoritmos paralelos

También hay algoritmos paralelos para árboles de búsqueda binarios, que incluyen insertar / eliminar múltiples elementos, construcción a partir de una matriz, filtrar con cierto predicador, aplanar a una matriz, fusionar / restar / intersecar dos árboles, etc. Estos algoritmos se pueden implementar usando uniones basadas en algoritmos de árbol , que también pueden mantener el árbol equilibrado mediante varios esquemas de equilibrio (incluido el árbol AVL , el árbol rojo-negro , el árbol con equilibrio de peso y el treap ).

Ejemplos de aplicaciones

Clasificar

Se puede utilizar un árbol de búsqueda binario para implementar un algoritmo de clasificación simple . Al igual que en heapsort , insertamos todos los valores que deseamos clasificar en una nueva estructura de datos ordenada, en este caso un árbol de búsqueda binaria, y luego lo recorremos en orden.

El momento del peor de los casos de build_binary_treees $O (n 2):$ si lo alimenta con una lista ordenada de valores, los encadena en una lista vinculada sin subárboles a la izquierda. Por ejemplo, build_binary_tree([1, 2, 3, 4, 5])cede el árbol (1 (2 (3 (4 (5))))).

Hay varios esquemas para superar esta falla con árboles binarios simples; el más común es el árbol de búsqueda binario autoequilibrado . Si este mismo procedimiento se realiza utilizando un árbol de este tipo, el tiempo total en el peor de los casos es $O (n log n)$ , que es asintóticamente óptimo para una clasificación de comparación . En la práctica, la sobrecarga adicional en tiempo y espacio para una ordenación basada en árboles (particularmente para la asignación de nodos ) la hace inferior a otras ordenaciones asintóticamente óptimas como heapsort para la ordenación de listas estáticas. Por otro lado, es uno de los métodos más eficientes de clasificación incremental , agregando elementos a una lista a lo largo del tiempo y manteniendo la lista ordenada en todo momento.

Operaciones de cola de prioridad

Los árboles de búsqueda binaria pueden servir como colas de prioridad : estructuras que permiten la inserción de claves arbitrarias, así como la búsqueda y eliminación de la clave mínima (o máxima). La inserción funciona como se explicó anteriormente. Find-min camina por el árbol, siguiendo los indicadores de la izquierda tanto como puede sin tocar una hoja:

// Precondition: T is not a leaf
function find-min(T):
    while hasLeft(T):
        T ? left(T)
    return key(T)

Find-max es análogo: siga los punteros de la derecha en la medida de lo posible. Delete-min ( max ) puede simplemente buscar el mínimo (máximo) y luego eliminarlo. De esta manera, tanto la inserción como la eliminación toman un tiempo logarítmico, tal como lo hacen en un montón binario , pero a diferencia de un montón binario y la mayoría de las otras implementaciones de colas de prioridad, un solo árbol puede admitir todos los archivos find-min , find-max , delete-min. y delete-max al mismo tiempo, lo que hace que los árboles de búsqueda binarios sean adecuados como colas de prioridad de dos extremos .

Tipos

Hay muchos tipos de árboles de búsqueda binarios. Los árboles AVL y los árboles rojo-negro son ambas formas de árboles de búsqueda binaria autoequilibrados . Un árbol de splay es un árbol de búsqueda binario que mueve automáticamente los elementos a los que se accede con frecuencia más cerca de la raíz. En un treap ( montón de árbol ), cada nodo también tiene una prioridad (elegida al azar) y el nodo padre tiene una prioridad más alta que sus hijos. Los árboles de tango son árboles optimizados para búsquedas rápidas. Los árboles T son árboles de búsqueda binarios optimizados para reducir la sobrecarga del espacio de almacenamiento, ampliamente utilizados para bases de datos en memoria.

Un árbol degenerado es un árbol donde para cada nodo padre, solo hay un nodo hijo asociado. Está desequilibrado y, en el peor de los casos, el rendimiento se degrada al de una lista vinculada. Si su función de agregar nodo no maneja el reequilibrio, entonces puede construir fácilmente un árbol degenerado alimentándolo con datos que ya están ordenados. Lo que esto significa es que en una medición de rendimiento, el árbol se comportará esencialmente como una estructura de datos de lista enlazada.

Comparaciones de desempeño

DA Heger (2004) presentó una comparación de rendimiento de árboles de búsqueda binarios. Se encontró que Treap tiene el mejor desempeño promedio, mientras que el árbol rojo-negro tiene el menor número de variaciones de desempeño.

Árboles de búsqueda binarios óptimos

Las rotaciones de árboles son operaciones internas muy comunes en árboles binarios para mantener un equilibrio interno perfecto o casi perfecto en el árbol.

Si no se pretende modificar un árbol de búsqueda y se sabe exactamente con qué frecuencia se accederá a cada elemento, es posible construir un árbol de búsqueda binario óptimo , que es un árbol de búsqueda donde el costo promedio de buscar un elemento ( el costo de búsqueda esperado ) se minimiza.

Incluso si solo tenemos estimaciones de los costos de búsqueda, dicho sistema puede acelerar considerablemente las búsquedas en promedio. Por ejemplo, si tenemos una BST de palabras en inglés utilizadas en un corrector ortográfico , podríamos equilibrar el árbol en función de la frecuencia de palabras en los corpus de texto , colocando palabras como the cerca de la raíz y palabras como agerasia cerca de las hojas. Tal árbol podría compararse con los árboles de Huffman , que de manera similar buscan colocar elementos de uso frecuente cerca de la raíz para producir una codificación de información densa; sin embargo, los árboles de Huffman almacenan elementos de datos solo en hojas y no es necesario ordenar estos elementos.

Si la secuencia en la que se accederá a los elementos del árbol se desconoce de antemano, se pueden usar árboles de splay que son asintóticamente tan buenos como cualquier árbol de búsqueda estática que podamos construir para cualquier secuencia particular de operaciones de búsqueda.

Los árboles alfabéticos son árboles de Huffman con la restricción adicional de orden o, de manera equivalente, árboles de búsqueda con la modificación de que todos los elementos se almacenan en las hojas. Existen algoritmos más rápidos para árboles binarios alfabéticos óptimos (OABT).

Ver también

Notas

Referencias

Otras lecturas

Este artículo incorpora material de dominio público del documento NIST : Black, Paul E. "Binary Search Tree" . Diccionario de algoritmos y estructuras de datos .
Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford (2001). "12: árboles de búsqueda binaria, 15,5: árboles de búsqueda binaria óptimos". Introducción a los algoritmos (2ª ed.). MIT Press y McGraw-Hill. págs. 253–272, 356–363. ISBN 0-262-03293-7.
Jarc, Duane J. (3 de diciembre de 2005). "Recorridos de árboles binarios" . Visualizaciones de estructura de datos interactivas . Universidad de Maryland . Archivado desde el original el 27 de febrero de 2014 . Consultado el 30 de abril de 2006 .
Knuth, Donald (1997). "6.2.2: Búsqueda de árbol binario". El arte de la programación informática . 3: "Ordenar y buscar" (3ª ed.). Addison-Wesley. págs. 426–458. ISBN 0-201-89685-0.
Largo, Sean. "Árbol de búsqueda binaria" ( PPT ) . Visualización de estructuras de datos y algoritmos: un enfoque basado en diapositivas de PowerPoint . SUNY Oneonta .
Parlante, Nick (2001). "Árboles binarios" . Biblioteca de educación de CS . Universidad de Stanford .

enlaces externos

Ben Pfaff: Introducción a los árboles de búsqueda binaria y los árboles equilibrados . (PDF; 1675 kB) 2004.
Visualizador de árbol binario (animación JavaScript de varias estructuras de datos basadas en BT)

Languages

In other projects