Folio de Descartes - Folium of Descartes

El folio de Descartes (verde) con asíntota (azul) cuando

{\ Displaystyle a = 1}

En geometría , el folio de Descartes es una curva algebraica definida por la ecuación

{\ Displaystyle x ^ {3} + y ^ {3} -3axy = 0 \,}

.

El nombre proviene de la palabra latina folium que significa " hoja ".

Historia

La curva fue propuesta y estudiada por primera vez por René Descartes en 1638. Su fama radica en un incidente en el desarrollo del cálculo . Descartes desafió a Pierre de Fermat a encontrar la línea tangente a la curva en un punto arbitrario, ya que Fermat había descubierto recientemente un método para encontrar líneas tangentes. Fermat resolvió el problema fácilmente, algo que Descartes no pudo hacer. Desde la invención del cálculo, la pendiente de la recta tangente se puede encontrar fácilmente mediante la diferenciación implícita .

Graficar la curva

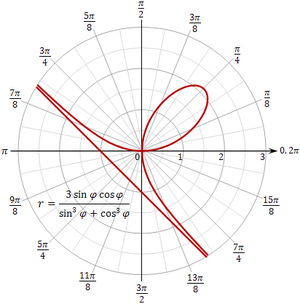
Folio de Descartes en coordenadas polares

El folio de Descartes se puede expresar en coordenadas polares como

{\ Displaystyle r = {\ frac {3a \ sin \ theta \ cos \ theta} {\ sin ^ {3} \ theta + \ cos ^ {3} \ theta}},}

que se traza a la izquierda. Esto es equivalente a

${\ Displaystyle r = {\ frac {3a \ sec \ theta \ tan \ theta} {1+ \ tan ^ {3} \ theta}}.}$

Otra técnica es escribir y resolver por y en términos de . Esto produce las ecuaciones paramétricas racionales : ${\ Displaystyle y = px}$ ${\ Displaystyle x}$ ${\ Displaystyle y}$ ${\ Displaystyle p}$

${\ displaystyle x = {{3ap} \ over {1 + p ^ {3}}}, \, y = {{3ap ^ {2}} \ over {1 + p ^ {3}}}}$ .

Podemos ver que el parámetro está relacionado con la posición en la curva de la siguiente manera:

${\ Displaystyle p <-1}$ corresponde a , : la derecha, inferior, "ala". ${\ Displaystyle x> 0}$ ${\ Displaystyle y <0}$
${\ Displaystyle -1 <p <0}$ corresponde a , : la izquierda, "ala" superior. ${\ Displaystyle x <0}$ ${\ Displaystyle y> 0}$
${\ Displaystyle p> 0}$ corresponde a , : el bucle de la curva. ${\ Displaystyle x> 0}$ ${\ Displaystyle y> 0}$

Otra forma de graficar la función se puede derivar de la simetría . La simetría se puede ver directamente en su ecuación (xey se pueden intercambiar). Al aplicar una rotación de 45 ° CW, por ejemplo, se puede trazar la función simétrica sobre el eje x girado. ${\ Displaystyle y = x}$

Esta operación es equivalente a una sustitución:

{\ Displaystyle x = {{u + v} \ over {\ sqrt {2}}}, \, y = {{uv} \ over {\ sqrt {2}}}}

y rinde

{\ Displaystyle v = \ pm u {\ sqrt {\ frac {3a {\ sqrt {2}} - 2u} {6u + 3a {\ sqrt {2}}}}}}

El trazado en el sistema cartesiano de da el folio girado 45 ° y, por lo tanto, simétrico por eje. ${\ Displaystyle (u, v)}$ ${\ Displaystyle u}$

Propiedades

Forma un bucle en el primer cuadrante con doble punto en el origen y asíntota.

{\ Displaystyle x + y + a = 0 \,}

.

Es simétrico con respecto a la línea . Como tal, los dos se cruzan en el origen y en el punto . ${\ Displaystyle y = x}$ ${\ Displaystyle (3a / 2,3a / 2)}$

La diferenciación implícita da la fórmula para que la pendiente de la recta tangente a esta curva sea

${\ Displaystyle {\ frac {dy} {dx}} = {\ frac {ay-x ^ {2}} {y ^ {2} -ax}}}$

Usando cualquiera de las representaciones polares anteriores, se encuentra que el área del interior del bucle es . Además, el área entre las "alas" de la curva y su asíntota inclinada también lo es . ${\ Displaystyle 3a ^ {2} / 2}$ ${\ Displaystyle 3a ^ {2} / 2}$

Relación con la trisectriz de Maclaurin

Trisectriz de Maclaurin

El folio de Descartes se relaciona con la trisectriz de Maclaurin por transformación afín . Para ver esto, comience con la ecuación

{\ Displaystyle x ^ {3} + y ^ {3} = 3axy \,}

,

y cambiar las variables para encontrar la ecuación en un sistema de coordenadas girado 45 grados. Esto equivale a establecer

{\ Displaystyle x = {{X + Y} \ over {\ sqrt {2}}}, y = {{XY} \ over {\ sqrt {2}}}.}

En el plano, la ecuación es ${\ Displaystyle X, Y}$

{\ Displaystyle 2X (X ^ {2} + 3Y ^ {2}) = 3 {\ sqrt {2}} a (X ^ {2} -Y ^ {2})}

.

Si estiramos la curva en la dirección en un factor de este se convierte en ${\ Displaystyle Y}$ ${\ Displaystyle {\ sqrt {3}}}$

{\ Displaystyle 2X (X ^ {2} + Y ^ {2}) = a {\ sqrt {2}} (3X ^ {2} -Y ^ {2}),}

que es la ecuación de la trisectriz de Maclaurin.

Notas

Referencias

J. Dennis Lawrence: Un catálogo de curvas planas especiales , 1972, Publicaciones de Dover. ISBN 0-486-60288-5 , págs. 106-108
George F. Simmons : Calculus Gems: Brief Lives and Memorable Mathematics , Nueva York 1992, McGraw-Hill, xiv, 355. ISBN 0-07-057566-5 ; nueva edición 2007, The Mathematical Association of America ( MAA )

Languages

In other projects