Prisma apeirogonal - Apeirogonal prism
| Prisma apeirogonal | |
|---|---|
 |
|
| Tipo | Azulejos semirregulares |
| Configuración de vértice |
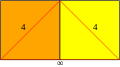 4.4.∞ |
| Símbolo Schläfli | t {2, ∞} |
| Símbolo de Wythoff | 2 ∞ | 2 |
| Diagrama de Coxeter |
   
|
| Simetría | [∞, 2], (* ∞22) |
| Simetría de rotación | [∞, 2] + , (∞22) |
| Acrónimo de Bowers | Azip |
| Doble | Bipirámide apeirogonal |
| Propiedades | Vértice-transitivo |
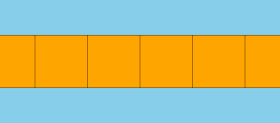
En geometría , un prisma apeirogonal o prisma infinito es el límite aritmético de la familia de prismas ; se puede considerar un poliedro infinito o un mosaico del plano.
Thorold Gosset lo llamó un semi-cheque bidimensional , como una sola fila de un tablero de ajedrez .
Si los lados son cuadrados , es un mosaico uniforme . Si se colorea con dos conjuntos de cuadrados alternos, sigue siendo uniforme.
Variante uniforme con caras cuadradas de colores alternos.
Su doble mosaico es una bipirámide apeirogonal .
Azulejos y poliedros relacionados
El mosaico apeirogonal es el límite aritmético de la familia de prismas t {2, p } o p .4.4, ya que p tiende al infinito , convirtiendo así el prisma en un mosaico euclidiano.
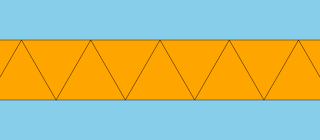
Una operación de alternancia puede crear un antiprisma apeirogonal compuesto por tres triángulos y un apeirogon en cada vértice.
De manera similar a los poliedros uniformes y los mosaicos uniformes , se pueden basar ocho mosaicos uniformes a partir del mosaico apeirogonal regular . Se duplican las formas rectificadas y canteladas , y como dos veces infinito es también infinito, también se duplican las formas truncadas y omnitruncadas , reduciendo a cuatro el número de formas únicas: el alicatado apeirogonal, el hosoedro apeirogonal, el prisma apeirogonal y el antiprisma apeirogonal .
| (∞ 2 2) | Padre | Truncado | Rectificado | Bitruncado | Birectificado (dual) |
Cantelado | Omnitruncated ( Cantitruncated ) |
Desaire |
|---|---|---|---|---|---|---|---|---|
| Wythoff | 2 | ∞ 2 | 2 2 | ∞ | 2 | ∞ 2 | 2 ∞ | 2 | ∞ | 2 2 | ∞ 2 | 2 | ∞ 2 2 | | | ∞ 2 2 |
| Schläfli | {∞, 2} | t {∞, 2} | r {∞, 2} | t {2, ∞} | {2, ∞} | rr {∞, 2} | tr {∞, 2} | sr {∞, 2} |
| Coxeter |
|
|
|
|
|
|
|
|
| Imagen figura de vértice |
 {∞, 2} |
∞.∞ |
∞.∞ |
4.4.∞ |
 {2, ∞} |
4.4.∞ |
 4.4.∞ |
 3.3.3.∞ |
Notas
Referencias
- T.Gosset : Sobre las figuras regulares y semi-regulares en el espacio de n dimensiones , Messenger of Mathematics, Macmillan, 1900
- Grünbaum, Branko ; Shephard, GC (1987). Azulejos y Patrones . WH Freeman and Company. ISBN 0-7167-1193-1 .
- Las simetrías de las cosas 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
 |
Este artículo relacionado con el poliedro es un trozo . Puedes ayudar a Wikipedia expandiéndolo . |