máquina de turing -Turing machine
Una máquina de Turing es un modelo matemático de computación que describe una máquina abstracta que manipula símbolos en una tira de cinta de acuerdo con una tabla de reglas. A pesar de la simplicidad del modelo, es capaz de implementar cualquier algoritmo informático .
La máquina opera en una cinta de memoria infinita dividida en celdas discretas , cada una de las cuales puede contener un solo símbolo extraído de un conjunto finito de símbolos llamado el alfabeto de la máquina. Tiene una "cabeza" que, en cualquier punto de la operación de la máquina, se coloca sobre una de estas celdas y un "estado" seleccionado de un conjunto finito de estados. En cada paso de su operación, la cabeza lee el símbolo en su celda. Luego, según el símbolo y el estado actual de la máquina, la máquina escribe un símbolo en la misma celda y mueve la cabeza un paso hacia la izquierda o hacia la derecha, o detiene el cálculo. La elección de qué símbolo de reemplazo escribir y en qué dirección moverse se basa en una tabla finita que especifica qué hacer para cada combinación del estado actual y el símbolo que se lee.
La máquina de Turing fue inventada en 1936 por Alan Turing , quien la llamó "a-machine" (máquina automática). Fue el asesor de doctorado de Turing, Alonzo Church , quien más tarde acuñó el término "máquina de Turing" en una reseña. Con este modelo, Turing pudo responder negativamente a dos preguntas:
- ¿Existe una máquina que pueda determinar si alguna máquina arbitraria en su cinta es "circular" (por ejemplo, se congela o no continúa con su tarea computacional)?
- ¿Existe una máquina que pueda determinar si alguna máquina arbitraria en su cinta alguna vez imprime un símbolo dado?
Por lo tanto, al proporcionar una descripción matemática de un dispositivo muy simple capaz de realizar cálculos arbitrarios, pudo probar las propiedades de la computación en general y, en particular, la incomputabilidad del Entscheidungsproblem ("problema de decisión").
Las máquinas de Turing demostraron la existencia de limitaciones fundamentales en el poder de la computación mecánica. Si bien pueden expresar cálculos arbitrarios, su diseño minimalista los hace inadecuados para el cálculo en la práctica: las computadoras del mundo real se basan en diferentes diseños que, a diferencia de las máquinas de Turing, usan memoria de acceso aleatorio .
La completitud de Turing es la capacidad de un sistema de instrucciones para simular una máquina de Turing. Un lenguaje de programación que es Turing completo es teóricamente capaz de expresar todas las tareas que pueden realizar las computadoras; casi todos los lenguajes de programación son Turing completos si se ignoran las limitaciones de la memoria finita.
Visión general
Una máquina de Turing es un ejemplo general de una unidad central de procesamiento (CPU) que controla toda la manipulación de datos realizada por una computadora, y la máquina canónica usa memoria secuencial para almacenar datos. Más específicamente, es una máquina ( autómata ) capaz de enumerar algún subconjunto arbitrario de cadenas válidas de un alfabeto ; estas cadenas son parte de un conjunto recursivamente enumerable . Una máquina de Turing tiene una cinta de longitud infinita en la que puede realizar operaciones de lectura y escritura.
Suponiendo una caja negra , la máquina de Turing no puede saber si eventualmente enumerará una cadena específica del subconjunto con un programa dado. Esto se debe al hecho de que el problema de la detención no tiene solución, lo que tiene importantes implicaciones para los límites teóricos de la computación.
La máquina de Turing es capaz de procesar una gramática sin restricciones , lo que implica además que es capaz de evaluar sólidamente la lógica de primer orden en un número infinito de formas. Esto se demuestra a través del cálculo lambda .
Una máquina de Turing que es capaz de simular cualquier otra máquina de Turing se llama máquina de Turing universal (UTM, o simplemente máquina universal). Alonzo Church introdujo una definición más orientada matemáticamente con una naturaleza "universal" similar , cuyo trabajo sobre el cálculo lambda se entrelazó con el de Turing en una teoría formal de la computación conocida como la tesis de Church-Turing . La tesis afirma que las máquinas de Turing capturan la noción informal de métodos efectivos en lógica y matemáticas y proporcionan un modelo a través del cual se puede razonar sobre un algoritmo o "procedimiento mecánico". El estudio de sus propiedades abstractas arroja muchas ideas sobre la informática y la teoría de la complejidad .
Descripción física
En su ensayo de 1948, "Maquinaria inteligente", Turing escribió que su máquina consistía en:
...una capacidad de memoria ilimitada obtenida en forma de una cinta infinita marcada en cuadrados, en cada uno de los cuales se podía imprimir un símbolo. En cualquier momento hay un símbolo en la máquina; se llama el símbolo escaneado. La máquina puede alterar el símbolo escaneado y su comportamiento está determinado en parte por ese símbolo, pero los símbolos en la cinta en otros lugares no afectan el comportamiento de la máquina. Sin embargo, la cinta se puede mover de un lado a otro a través de la máquina, siendo esta una de las operaciones elementales de la máquina. Por lo tanto, cualquier símbolo en la cinta puede eventualmente tener una entrada.
— Turing 1948, pág. 3
Descripción
La máquina de Turing modela matemáticamente una máquina que opera mecánicamente sobre una cinta. En esta cinta hay símbolos que la máquina puede leer y escribir, uno a la vez, utilizando un cabezal de cinta. La operación está totalmente determinada por un conjunto finito de instrucciones elementales como "en el estado 42, si el símbolo que se ve es 0, escriba un 1; si el símbolo que se ve es 1, cambie al estado 17; en el estado 17, si el símbolo que se ve es 0, escribe un 1 y cambia al estado 6;" etc. En el artículo original (" Sobre los números computables, con una aplicación al problema Entscheidungs ", ver también las referencias a continuación ), Turing no imagina un mecanismo, sino una persona a la que llama "computadora", que ejecuta estas reglas mecánicas deterministas servilmente. (o como dice Turing, "de una manera inconexa").

Más explícitamente, una máquina de Turing consta de:
- Una cinta dividida en celdas, una al lado de la otra. Cada celda contiene un símbolo de algún alfabeto finito. El alfabeto contiene un símbolo especial en blanco (aquí escrito como '0') y uno o más símbolos. Se supone que la cinta se puede extender arbitrariamente hacia la izquierda y hacia la derecha, de modo que la máquina de Turing siempre recibe tanta cinta como necesita para su cálculo. Se supone que las celdas que no se han escrito antes se llenan con el símbolo en blanco. En algunos modelos, la cinta tiene un extremo izquierdo marcado con un símbolo especial; la cinta se extiende o es indefinidamente extensible hacia la derecha.
- Un cabezal que puede leer y escribir símbolos en la cinta y mover la cinta hacia la izquierda y hacia la derecha una (y solo una) celda a la vez. En algunos modelos, la cabeza se mueve y la cinta está fija.
- Un registro de estado que almacena el estado de la máquina de Turing, uno de muchos. Entre estos está el estado de inicio especial con el que se inicializa el registro de estado. Estos estados, escribe Turing, reemplazan el "estado mental" en el que normalmente se encontraría una persona que realiza cálculos.
- Una tabla finita de instrucciones que, dado el estado (q i ) en el que se encuentra actualmente la máquina y el símbolo (a j ) que está leyendo en la cinta (símbolo actualmente debajo del encabezado), le dice a la máquina que haga lo siguiente en secuencia ( para los modelos de 5 tuplas):
- Borre o escriba un símbolo (reemplazando una j con una j1 ).
- Mueva la cabeza (que se describe mediante d k y puede tener valores: 'L' para un paso a la izquierda o 'R' para un paso a la derecha o 'N' para permanecer en el mismo lugar).
- Suponga el mismo estado o uno nuevo según lo prescrito (vaya al estado q i1 ).
En los modelos de 4 tuplas, borrar o escribir un símbolo (a j1 ) y mover la cabeza hacia la izquierda o hacia la derecha (d k ) se especifican como instrucciones separadas. La tabla le dice a la máquina que (ia) borre o escriba un símbolo o (ib) mueva la cabeza hacia la izquierda o hacia la derecha, y luego (ii) asuma el mismo estado o uno nuevo según lo prescrito, pero no ambas acciones (ia) y (ib) ) en la misma instrucción. En algunos modelos, si no hay una entrada en la tabla para la combinación actual de símbolo y estado, la máquina se detendrá; otros modelos requieren que se llenen todas las entradas.
Cada parte de la máquina (es decir, su estado, colección de símbolos y cinta usada en un momento dado) y sus acciones (como imprimir, borrar y mover la cinta) es finita , discreta y distinguible ; es la cantidad ilimitada de cinta y tiempo de ejecución lo que le da una cantidad ilimitada de espacio de almacenamiento .
Definicion formal
Siguiendo a Hopcroft & Ullman (1979 , p. 148) , una máquina de Turing (de una cinta) puede definirse formalmente como una tupla de 7 donde
- es un conjunto finito y no vacío de símbolos alfabéticos de cinta ;
- es el símbolo en blanco (el único símbolo permitido en la cinta con una frecuencia infinita en cualquier paso durante el cálculo);
- es el conjunto de símbolos de entrada , es decir, el conjunto de símbolos que pueden aparecer en el contenido inicial de la cinta;
- es un conjunto de estados finito, no vacío ;
- es el estado inicial ;
- es el conjunto de estados finales o estados de aceptación . Se dice que el contenido inicial de la cinta es aceptado por si finalmente se detiene en un estado de .
- es una función parcial llamada función de transición , donde L es el desplazamiento a la izquierda, R es el desplazamiento a la derecha. Si no está definido en el estado actual y el símbolo de cinta actual, la máquina se detiene; intuitivamente, la función de transición especifica el siguiente estado transitado desde el estado actual, qué símbolo sobrescribir el símbolo actual señalado por la cabeza y el próximo movimiento de la cabeza.
Además, la máquina de Turing también puede tener un estado de rechazo para que el rechazo sea más explícito. En ese caso hay tres posibilidades: aceptar, rechazar y correr para siempre. Otra posibilidad es considerar los valores finales de la cinta como salida. Sin embargo, si la única salida es el estado final en el que termina la máquina (o si nunca se detiene), la máquina aún puede generar efectivamente una cadena más larga tomando un número entero que le indica qué bit de la cadena generar.
Una variante relativamente poco común permite "sin cambio", digamos N, como un tercer elemento del conjunto de direcciones .
La tupla de 7 para el castor ocupado de 3 estados se ve así (vea más sobre este castor ocupado en los ejemplos de máquinas de Turing ):
- (estados);
- (símbolos del alfabeto de cinta);
- (símbolo en blanco);
- (símbolos de entrada);
- (estado inicial);
- (estados finales);
- consulte la tabla de estados a continuación (función de transición).
Inicialmente, todas las celdas de la cinta están marcadas con .
| Símbolo de cinta | Estado actual A | Estado actual B | Estado actual C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| escribir símbolo | Mover cinta | siguiente estado | escribir símbolo | Mover cinta | siguiente estado | escribir símbolo | Mover cinta | siguiente estado | |
| 0 | 1 | R | B | 1 | L | A | 1 | L | B |
| 1 | 1 | L | C | 1 | R | B | 1 | R | DETENER |
Se requieren detalles adicionales para visualizar o implementar máquinas de Turing
En palabras de van Emde Boas (1990), p. 6: "El objeto teórico de conjuntos [su descripción formal de siete tuplas similar a la anterior] proporciona solo información parcial sobre cómo se comportará la máquina y cómo serán sus cálculos".
Por ejemplo,
- Habrá que tomar muchas decisiones sobre el aspecto real de los símbolos y una forma infalible de leer y escribir símbolos indefinidamente.
- Las operaciones de desplazamiento hacia la izquierda y hacia la derecha pueden desplazar el cabezal de la cinta a través de la cinta, pero cuando se construye una máquina de Turing, es más práctico hacer que la cinta se deslice hacia adelante y hacia atrás debajo del cabezal.
- La cinta puede ser finita y extenderse automáticamente con espacios en blanco según sea necesario (que es lo más cercano a la definición matemática), pero es más común pensar que se estira infinitamente en uno o ambos extremos y se llena previamente con espacios en blanco excepto en el dado explícitamente el fragmento finito en el que se encuentra el cabezal de la cinta. (Esto, por supuesto, no se puede implementar en la práctica). La cinta no puede tener una longitud fija, ya que eso no correspondería a la definición dada y limitaría seriamente el rango de cálculos que la máquina puede realizar a los de un autómata lineal acotado si la cinta era proporcional al tamaño de entrada, o una máquina de estados finitos si tenía una longitud estrictamente fija.
Definiciones alternativas
Las definiciones en la literatura a veces difieren ligeramente, para hacer que los argumentos o las pruebas sean más fáciles o más claros, pero esto siempre se hace de tal manera que la máquina resultante tenga el mismo poder de cómputo. Por ejemplo, el conjunto podría cambiarse de a , donde N ("Ninguno" o "Sin operación") permitiría que la máquina permanezca en la misma celda de cinta en lugar de moverse hacia la izquierda o hacia la derecha. Esto no aumentaría la potencia computacional de la máquina.
La convención más común representa cada "instrucción de Turing" en una "tabla de Turing" mediante una de nueve tuplas de 5, según la convención de Turing/Davis (Turing (1936) en The Undecidable , p. 126–127 y Davis (2000) pág. 152):
- (definición 1): (q i , S j , S k /E/N, L/R/N, q m )
- ( estado actual q i , símbolo escaneado S j , imprimir símbolo S k /borrar E /ninguno N , mover_cinta_un_cuadrado izquierda L /derecha R /ninguno N , nuevo estado q m )
Otros autores (Minsky (1967) p. 119, Hopcroft y Ullman (1979) p. 158, Stone (1972) p. 9) adoptan una convención diferente, con el nuevo estado q m enumerado inmediatamente después del símbolo escaneado S j :
- (definición 2): (q i , S j , q m , S k /E/N, L/R/N)
- ( estado actual q i , símbolo escaneado S j , nuevo estado q m , imprimir símbolo S k /borrar E /ninguno N , mover_cinta_un_cuadrado izquierda L /derecha R /ninguno N )
Para el resto de este artículo se utilizará la "definición 1" (la convención de Turing/Davis).
| Estado actual | símbolo escaneado | Imprimir símbolo | Mover cinta | Estado final (es decir, siguiente) | 5 tuplas | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | R | B | ( A , 0, 1, R, B ) | |
| A | 1 | 1 | L | C | ( A , 1, 1, L, C ) | |
| B | 0 | 1 | L | A | ( B , 0, 1, L, A ) | |
| B | 1 | 1 | R | B | ( segundo , 1, 1, r, segundo ) | |
| C | 0 | 1 | L | B | ( C , 0, 1, L, B ) | |
| C | 1 | 1 | norte | H | ( C , 1, 1, N, H ) |
En la siguiente tabla, el modelo original de Turing permitía solo las primeras tres líneas que llamó N1, N2, N3 (cf. Turing en The Undecidable , p. 126). Permitió el borrado del "cuadrado escaneado" nombrando un símbolo 0 S 0 = "borrar" o "en blanco", etc. Sin embargo, no permitió la no impresión, por lo que cada línea de instrucción incluye "imprimir símbolo S k " o "borrar" (cf. nota al pie 12 en Post (1947), The Undecidable , p. 300). Las abreviaturas son de Turing ( The Undecidable , p. 119). Posteriormente al artículo original de Turing en 1936-1937, los modelos de máquinas han permitido los nueve tipos posibles de cinco tuplas:
| Configuración m actual (estado de Turing) |
Símbolo de cinta | operación de impresión | movimiento de cinta | Configuración m final (estado de Turing) |
tupla de 5 | comentarios de 5 tuplas | tupla de 4 | |
|---|---|---|---|---|---|---|---|---|
| N1 | q yo | s j | Imprimir ( Sk ) | Izquierda L | q metro | (q yo , S j , S k , L, q m ) | "en blanco" = S 0 , 1=S 1 , etc. | |
| N2 | q yo | s j | Imprimir ( Sk ) | Derecha R | q metro | (q yo , S j , S k , R, q m ) | "en blanco" = S 0 , 1=S 1 , etc. | |
| N3 | q yo | s j | Imprimir ( Sk ) | Ninguno norte | q metro | (q yo , S j , S k , N, q metro ) | "en blanco" = S 0 , 1=S 1 , etc. | (q yo , S j , S k , q metro ) |
| 4 | q yo | s j | Ninguno norte | Izquierda L | q metro | (q i , S j , N, L, q m ) | (q yo , S j , L, q m ) | |
| 5 | q yo | s j | Ninguno norte | Derecha R | q metro | (q i , S j , N, R, q m ) | (q yo , S j , R, q m ) | |
| 6 | q yo | s j | Ninguno norte | Ninguno norte | q metro | (q yo , S j , N, N, q m ) | Directo "salto" | (q yo , S j , N, q m ) |
| 7 | q yo | s j | Borrar | Izquierda L | q metro | (q i , S j , E, L, q m ) | ||
| 8 | q yo | s j | Borrar | Derecha R | q metro | (q i , S j , E, R, q m ) | ||
| 9 | q yo | s j | Borrar | Ninguno norte | q metro | (q i , S j , E, N, q m ) | (q i , S j , E, q m ) |
Cualquier tabla de Turing (lista de instrucciones) se puede construir a partir de las nueve 5 tuplas anteriores. Por razones técnicas, normalmente se pueden prescindir de las tres instrucciones no imprimibles o "N" (4, 5, 6). Para ver ejemplos, consulte Ejemplos de máquinas de Turing .
Con menos frecuencia se encuentra el uso de tuplas de 4: estas representan una atomización adicional de las instrucciones de Turing (cf. Post (1947), Boolos & Jeffrey (1974, 1999), Davis-Sigal-Weyuker (1994)); también vea más en Post–Turing machine .
El estado"
La palabra "estado" utilizada en el contexto de las máquinas de Turing puede ser fuente de confusión, ya que puede significar dos cosas. La mayoría de los comentaristas posteriores a Turing han usado "estado" para referirse al nombre/designador de la instrucción actual a ejecutar, es decir, el contenido del registro de estado. Pero Turing (1936) hizo una fuerte distinción entre un registro de lo que llamó la "configuración m" de la máquina y el "estado de progreso" de la máquina (o de la persona) a través del cálculo: el estado actual del sistema total. Lo que Turing llamó "la fórmula del estado" incluye tanto la instrucción actual como todos los símbolos de la cinta:
Así, el estado de progreso del cálculo en cualquier etapa está completamente determinado por la nota de instrucciones y los símbolos en la cinta. Es decir, el estado del sistema puede describirse mediante una sola expresión (secuencia de símbolos) que consta de los símbolos en la cinta seguidos de Δ (que se supone que no aparece en ningún otro lugar) y luego por la nota de instrucciones. Esta expresión se llama "fórmula de estado".
— The Undecidable , págs. 139–140, énfasis añadido
Anteriormente, en su artículo, Turing llevó esto aún más lejos: da un ejemplo en el que colocó un símbolo de la "configuración m" actual, la etiqueta de la instrucción, debajo del cuadrado escaneado, junto con todos los símbolos en la cinta ( The Undecidable , p. . 121); a esto él lo llama "la configuración completa " ( The Undecidable , p. 118). Para imprimir la "configuración completa" en una línea, coloca la etiqueta de estado/configuración m a la izquierda del símbolo escaneado.
Una variante de esto se ve en Kleene (1952), donde Kleene muestra cómo escribir el número de Gödel de la "situación" de una máquina: coloca el símbolo de "configuración m" q 4 sobre el cuadrado escaneado aproximadamente en el centro de los 6 no -cuadrados en blanco en la cinta (vea la figura de la cinta de Turing en este artículo) y lo coloca a la derecha del cuadrado escaneado. Pero Kleene se refiere a "q 4 " en sí mismo como "el estado de la máquina" (Kleene, p. 374-375). Hopcroft y Ullman llaman a este compuesto la "descripción instantánea" y siguen la convención de Turing de poner el "estado actual" (instrucción-etiqueta, m-configuración) a la izquierda del símbolo escaneado (p. 149), es decir, el instantáneo la descripción es la combinación de símbolos que no están en blanco a la izquierda, el estado de la máquina, el símbolo actual escaneado por el cabezal y los símbolos que no están en blanco a la derecha.
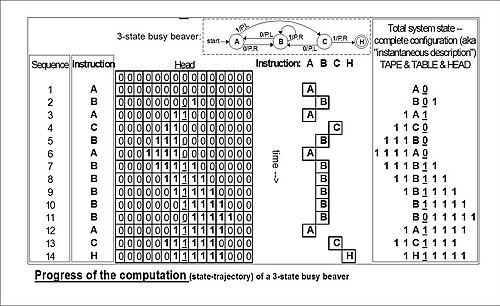
Ejemplo: estado total del castor ocupado de 3 estados y 2 símbolos después de 3 "movimientos" (tomado del ejemplo "ejecutar" en la siguiente figura):
- 1 un 1
Esto significa: después de tres movimientos, la cinta tiene ... 000110000 ... en ella, la cabeza está escaneando el 1 más a la derecha y el estado es A . Los espacios en blanco (en este caso representados por "0") pueden ser parte del estado total como se muestra aquí: B 01; la cinta tiene un solo 1, pero la cabeza está escaneando el 0 ("en blanco") a su izquierda y el estado es B.
El "estado" en el contexto de las máquinas de Turing debe aclararse en cuanto a lo que se describe: la instrucción actual, o la lista de símbolos en la cinta junto con la instrucción actual, o la lista de símbolos en la cinta junto con la instrucción actual colocado a la izquierda del símbolo escaneado o a la derecha del símbolo escaneado.
El biógrafo de Turing, Andrew Hodges (1983: 107) ha señalado y discutido esta confusión.
Diagramas de "estado"
| Símbolo de cinta | Estado actual A | Estado actual B | Estado actual C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| escribir símbolo | Mover cinta | siguiente estado | escribir símbolo | Mover cinta | siguiente estado | escribir símbolo | Mover cinta | siguiente estado | |
| 0 | PAGS | R | B | PAGS | L | A | PAGS | L | B |
| 1 | PAGS | L | C | PAGS | R | B | PAGS | R | DETENER |

A la derecha: la tabla anterior expresada como un diagrama de "transición de estado".
Por lo general, es mejor dejar las mesas grandes como mesas (Booth, p. 74). Se simulan más fácilmente por computadora en forma tabular (Booth, p. 74). Sin embargo, ciertos conceptos, por ejemplo, máquinas con estados de "reinicio" y máquinas con patrones repetitivos (cf. Hill y Peterson p. 244ff), se pueden ver más fácilmente cuando se ven como un dibujo.
El lector debe decidir si un dibujo representa una mejora en su tabla para el contexto particular.
Se debe advertir nuevamente al lector que tales diagramas representan una instantánea de su tabla congelada en el tiempo, no el curso ("trayectoria") de un cálculo a través del tiempo y el espacio. Si bien cada vez que la máquina castor ocupada "ejecuta", siempre seguirá la misma trayectoria de estado, esto no es cierto para la máquina de "copia" que puede proporcionarse con "parámetros" de entrada variable.
El diagrama "progreso del cálculo" muestra el progreso del "estado" (instrucción) del castor ocupado de tres estados a través de su cálculo de principio a fin. En el extremo derecho está la "configuración completa" de Turing ("situación" de Kleene, "descripción instantánea" de Hopcroft-Ullman) en cada paso. Si se detuviera la máquina y se borrara tanto el "registro de estado" como toda la cinta, estas "configuraciones" podrían usarse para reavivar un cómputo en cualquier parte de su progreso (cf. Turing (1936) The Undecidable , pp. 139– 140).
Modelos equivalentes
Se puede demostrar que muchas máquinas de las que se podría pensar que tienen más capacidad computacional que una simple máquina universal de Turing no tienen más poder (Hopcroft y Ullman p. 159, cf. Minsky (1967)). Quizás calculen más rápido, o usen menos memoria, o su conjunto de instrucciones sea más pequeño, pero no pueden computar con mayor potencia (es decir, más funciones matemáticas). (La tesis de Church-Turing plantea la hipótesis de que esto es cierto para cualquier tipo de máquina: que cualquier cosa que pueda "computarse" puede ser computada por alguna máquina de Turing).
Una máquina de Turing es equivalente a un autómata pushdown de una sola pila (PDA) que se ha vuelto más flexible y conciso al relajar el requisito de último en entrar, primero en salir (LIFO) de su pila. Además, una máquina de Turing también es equivalente a una PDA de dos pilas con semántica LIFO estándar, ya que usa una pila para modelar la cinta a la izquierda del cabezal y la otra pila para la cinta a la derecha.
En el otro extremo, algunos modelos muy simples resultan ser equivalentes a Turing , es decir, tienen el mismo poder computacional que el modelo de la máquina de Turing.
Los modelos equivalentes comunes son la máquina de Turing de múltiples cintas, la máquina de Turing de múltiples pistas , las máquinas con entrada y salida, y la máquina de Turing no determinista (NDTM) en oposición a la máquina de Turing determinista (DTM) para la cual la tabla de acción tiene en más una entrada para cada combinación de símbolo y estado.
Las máquinas de Turing de movimiento hacia la derecha de solo lectura son equivalentes a los DFA (así como a los NFA mediante la conversión mediante el algoritmo de conversión de NDFA a DFA ).
Para propósitos prácticos y didácticos, la máquina de registro equivalente puede usarse como un lenguaje de programación ensamblador habitual .
Una pregunta relevante es si el modelo de computación representado por lenguajes de programación concretos es o no equivalente a Turing. Si bien el cálculo de una computadora real se basa en estados finitos y, por lo tanto, no es capaz de simular una máquina de Turing, los lenguajes de programación en sí mismos no necesariamente tienen esta limitación. Kirner et al., 2009 han demostrado que entre los lenguajes de programación de propósito general, algunos son Turing completos mientras que otros no. Por ejemplo, ANSI C no es equivalente a Turing, ya que todas las instancias de ANSI C (son posibles diferentes instancias ya que el estándar deja deliberadamente cierto comportamiento sin definir por razones heredadas) implica una memoria de espacio finito. Esto se debe a que el tamaño de los tipos de datos de referencia de memoria, llamados punteros , es accesible dentro del lenguaje. Sin embargo, otros lenguajes de programación como Pascal no tienen esta característica, lo que les permite ser Turing completos en principio. En principio, es solo Turing completo, ya que se permite que falle la asignación de memoria en un lenguaje de programación, lo que significa que el lenguaje de programación puede ser Turing completo al ignorar las asignaciones de memoria fallidas, pero los programas compilados ejecutables en una computadora real no pueden.
Choice c-máquinas, oráculo o-máquinas
Al principio de su artículo (1936), Turing hace una distinción entre una "máquina automática": su "movimiento ... completamente determinado por la configuración" y una "máquina de elección":
... cuyo movimiento está determinado solo parcialmente por la configuración ... Cuando una máquina de este tipo alcanza una de estas configuraciones ambiguas, no puede continuar hasta que un operador externo haya realizado una elección arbitraria. Este sería el caso si estuviéramos usando máquinas para tratar con sistemas axiomáticos.
— Lo indecidible , pág. 118
Turing (1936) no da más detalles excepto en una nota a pie de página en la que describe cómo usar una máquina a para "encontrar todas las fórmulas comprobables del cálculo [de Hilbert]" en lugar de usar una máquina de elección. Él "supone que las opciones están siempre entre dos posibilidades 0 y 1. Cada prueba estará determinada por una secuencia de opciones i 1 , i 2 , ..., i n (i 1 = 0 o 1, i 2 = 0 o 1, ..., i n = 0 o 1), y por lo tanto el número 2 n + i 1 2 n-1 + i 2 2 n-2 + ... +i n determina completamente la prueba. La máquina automática realiza sucesivamente prueba 1, prueba 2, prueba 3,..." (Nota ‡, El Indecidible , p. 138)
De hecho, esta es la técnica mediante la cual se puede utilizar una máquina de Turing determinista (es decir, a-) para imitar la acción de una máquina de Turing no determinista ; Turing resolvió el asunto en una nota a pie de página y parece descartarlo para futuras consideraciones.
Una máquina de oráculo o máquina-o es una máquina-a de Turing que detiene su cálculo en el estado " o " mientras que, para completar su cálculo, "espera la decisión" del "oráculo", una entidad no especificada "aparte de decir que no puede ser una máquina" (Turing (1939), The Undecidable , p. 166-168).
Máquinas de Turing universales
Como escribió Turing en The Undecidable , p. 128 (cursivas añadidas):
Es posible inventar una sola máquina que pueda usarse para calcular cualquier secuencia computable. Si a esta máquina U se le suministra la cinta en cuyo comienzo está escrita la cadena de quíntuplos separados por punto y coma de alguna máquina de computación M , entonces U computará la misma secuencia que M.
Este hallazgo ahora se da por sentado, pero en ese momento (1936) se consideró asombroso. El modelo de computación que Turing llamó su "máquina universal" (" U " para abreviar) es considerado por algunos (cf. Davis (2000)) como el avance teórico fundamental que condujo a la noción de computadora con programa almacenado .
El artículo de Turing... contiene, en esencia, la invención de la computadora moderna y algunas de las técnicas de programación que la acompañaron.
— Minsky (1967), pág. 104
En términos de complejidad computacional , una máquina de Turing universal de múltiples cintas solo necesita ser más lenta por un factor logarítmico en comparación con las máquinas que simula. Este resultado fue obtenido en 1966 por FC Hennie y RE Stearns . (Arora y Barak, 2009, teorema 1.9)
Comparación con máquinas reales

A menudo se cree que las máquinas de Turing, a diferencia de los autómatas más simples, son tan poderosas como las máquinas reales y pueden ejecutar cualquier operación que pueda ejecutar un programa real. Lo que se pasa por alto en esta declaración es que, debido a que una máquina real solo puede tener un número finito de configuraciones , no es más que una máquina de estado finito , mientras que una máquina de Turing tiene una cantidad ilimitada de espacio de almacenamiento disponible para sus cálculos.
Hay varias formas de explicar por qué las máquinas de Turing son modelos útiles de computadoras reales:
- Cualquier cosa que una computadora real pueda calcular, una máquina de Turing también puede calcular. Por ejemplo: "Una máquina de Turing puede simular cualquier tipo de subrutina que se encuentre en los lenguajes de programación, incluidos los procedimientos recursivos y cualquiera de los mecanismos conocidos de paso de parámetros" (Hopcroft y Ullman p. 157). Una FSA lo suficientemente grande también puede modelar cualquier computadora real, sin tener en cuenta IO. Por lo tanto, una declaración sobre las limitaciones de las máquinas de Turing también se aplicará a las computadoras reales.
- La diferencia radica solo en la capacidad de una máquina de Turing para manipular una cantidad ilimitada de datos. Sin embargo, dada una cantidad finita de tiempo, una máquina de Turing (como una máquina real) solo puede manipular una cantidad finita de datos.
- Al igual que una máquina de Turing, una máquina real puede ampliar su espacio de almacenamiento según sea necesario, adquiriendo más discos u otros medios de almacenamiento.
- Las descripciones de programas de máquinas reales que utilizan modelos abstractos más simples suelen ser mucho más complejas que las descripciones que utilizan máquinas de Turing. Por ejemplo, una máquina de Turing que describe un algoritmo puede tener unos pocos cientos de estados, mientras que el autómata finito determinista (DFA) equivalente en una máquina real dada tiene cuatrillones. Esto hace que la representación DFA no sea factible de analizar.
- Las máquinas de Turing describen algoritmos independientemente de la cantidad de memoria que utilicen. Existe un límite para la memoria que posee cualquier máquina actual, pero este límite puede aumentar arbitrariamente con el tiempo. Las máquinas de Turing nos permiten hacer afirmaciones sobre algoritmos que (teóricamente) se mantendrán para siempre, independientemente de los avances en la arquitectura de las máquinas informáticas convencionales .
- Las máquinas de Turing simplifican la declaración de algoritmos. Los algoritmos que se ejecutan en máquinas abstractas equivalentes a Turing suelen ser más generales que sus contrapartes que se ejecutan en máquinas reales, porque tienen tipos de datos de precisión arbitraria disponibles y nunca tienen que lidiar con condiciones inesperadas (que incluyen, entre otros, quedarse sin memoria ) .
Limitaciones
Teoría de la complejidad computacional
Una limitación de las máquinas de Turing es que no modelan bien las fortalezas de un arreglo en particular. Por ejemplo, las computadoras modernas de programa almacenado son en realidad instancias de una forma más específica de máquina abstracta conocida como máquina de programa almacenado de acceso aleatorio o modelo de máquina RASP. Al igual que la máquina de Turing universal, el RASP almacena su "programa" en una "memoria" externa a las "instrucciones" de su máquina de estado finito. A diferencia de la máquina de Turing universal, el RASP tiene un número infinito de "registros" distinguibles, numerados pero ilimitados: "celdas" de memoria que pueden contener cualquier número entero (cf. Elgot y Robinson (1964), Hartmanis (1971) y, en particular, Cook -Rechow (1973); referencias en máquina de acceso aleatorio ). La máquina de estados finitos del RASP está equipada con la capacidad de direccionamiento indirecto (por ejemplo, el contenido de un registro puede usarse como una dirección para especificar otro registro); por lo tanto, el "programa" del RASP puede dirigirse a cualquier registro en la secuencia de registros. El resultado de esta distinción es que existen optimizaciones computacionales que se pueden realizar en función de los índices de memoria, que no son posibles en una máquina de Turing general; por lo tanto, cuando las máquinas de Turing se utilizan como base para acotar los tiempos de ejecución, se puede demostrar un "límite inferior falso" en los tiempos de ejecución de ciertos algoritmos (debido a la falsa suposición simplificadora de una máquina de Turing). Un ejemplo de esto es la búsqueda binaria , un algoritmo que se puede demostrar que funciona más rápido cuando se usa el modelo de cálculo RASP en lugar del modelo de la máquina de Turing.
concurrencia
Otra limitación de las máquinas de Turing es que no modelan bien la concurrencia . Por ejemplo, hay un límite en el tamaño de un entero que puede calcularse mediante una máquina de Turing no determinista que siempre se detiene y comienza en una cinta en blanco. (Consulte el artículo sobre no determinismo ilimitado ). Por el contrario, hay sistemas concurrentes que siempre se detienen sin entradas que pueden calcular un número entero de tamaño ilimitado. (Se puede crear un proceso con almacenamiento local que se inicializa con un conteo de 0 que se envía simultáneamente un mensaje de parada y uno de marcha. Cuando recibe un mensaje de marcha, incrementa su conteo en 1 y se envía a sí mismo un mensaje de marcha. Cuando recibe un mensaje de detención, se detiene con un número ilimitado en su almacenamiento local).
Interacción
En los primeros días de la informática, el uso de la computadora se limitaba típicamente al procesamiento por lotes , es decir, tareas no interactivas, cada una de las cuales producía datos de salida a partir de datos de entrada dados. La teoría de la computabilidad, que estudia la computabilidad de las funciones desde las entradas hasta las salidas, y para la cual se inventaron las máquinas de Turing, refleja esta práctica.
Desde la década de 1970, el uso interactivo de las computadoras se volvió mucho más común. En principio, es posible modelar esto haciendo que un agente externo lea la cinta y escriba en ella al mismo tiempo que una máquina de Turing, pero esto rara vez coincide con la forma en que realmente ocurre la interacción; por lo tanto, cuando se describe la interactividad, se suelen preferir alternativas como los autómatas de E/S .
Historia
Antecedentes históricos: maquinaria computacional
Robin Gandy (1919-1995), alumno de Alan Turing (1912-1954) y amigo de toda su vida, rastrea el linaje de la noción de "máquina calculadora" hasta Charles Babbage (alrededor de 1834) y, de hecho, propone la "Tesis de Babbage". :
Que todo el desarrollo y las operaciones de análisis ahora pueden ser ejecutados por maquinaria .
- (cursiva en Babbage citado por Gandy, p. 54)
El análisis de Gandy del motor analítico de Babbage describe las siguientes cinco operaciones (cf. p. 52-53):
- Las funciones aritméticas +, −, ×, donde − indica la resta "adecuada" x − y = 0 si y ≥ x .
- Cualquier secuencia de operaciones es una operación.
- Iteración de una operación (repetir n veces una operación P).
- Iteración condicional (repetir n veces una operación P condicionada al "éxito" de la prueba T).
- Transferencia condicional (es decir, " goto " condicional).
Gandy afirma que "las funciones que pueden calcularse mediante (1), (2) y (4) son precisamente aquellas que son computables por Turing ". (pág. 53). Cita otras propuestas de "máquinas calculadoras universales", incluidas las de Percy Ludgate (1909), Leonardo Torres y Quevedo (1914), Maurice d'Ocagne (1922), Louis Couffignal (1933), Vannevar Bush (1936), Howard Aiken ( 1937). Sin embargo:
… el énfasis está en programar una secuencia iterable fija de operaciones aritméticas. No se reconoce la importancia fundamental de la iteración condicional y la transferencia condicional para una teoría general de las máquinas calculadoras...
— Gandy pág. 55
El Entscheidungsproblem (el "problema de decisión"): la décima pregunta de Hilbert de 1900
Con respecto a los problemas de Hilbert planteados por el famoso matemático David Hilbert en 1900, un aspecto del problema n.º 10 había estado dando vueltas durante casi 30 años antes de que se enmarcara con precisión. La expresión original de Hilbert para el número 10 es la siguiente:
10. Determinación de la solucionabilidad de una ecuación diofántica . Dada una ecuación diofántica con cualquier cantidad de incógnitas y con coeficientes integrales racionales: Idear un proceso según el cual se pueda determinar en un número finito de operaciones si la ecuación es resoluble en números enteros racionales. El Entscheidungsproblem [problema de decisión para la lógica de primer orden ] se resuelve cuando conocemos un procedimiento que permite que cualquier expresión lógica dada decida mediante un número finito de operaciones su validez o satisfacibilidad... El Entscheidungsproblem debe considerarse el principal problema de la lógica matemática.
— citado, con esta traducción y el original en alemán, en Dershowitz y Gurevich, 2008
Para 1922, esta noción de " Entscheidungsproblem " se había desarrollado un poco, y H. Behmann afirmó que
... la forma más general del Entscheidungsproblem [es] como sigue:
Se requiere una prescripción general bastante definida que permita decidir en un número finito de pasos la verdad o falsedad de una afirmación puramente lógica dada...
— Gandy pág. 57, citando a Behmann
Behmann comenta que... el problema general es equivalente al problema de decidir qué proposiciones matemáticas son verdaderas.
— ibíd.
Si uno pudiera resolver el Entscheidungsproblem, entonces tendría un "procedimiento para resolver muchos (o incluso todos) los problemas matemáticos".
— ibíd. , pags. 92
Para el congreso internacional de matemáticos de 1928, Hilbert "hizo sus preguntas bastante precisas. Primero, ¿las matemáticas eran completas ... Segundo, las matemáticas eran consistentes ... Y tercero, ¿las matemáticas eran decidibles ?" (Hodges p. 91, Hawking p. 1121). Las dos primeras preguntas fueron respondidas en 1930 por Kurt Gödel en la misma reunión donde Hilbert pronunció su discurso de jubilación (para disgusto de Hilbert); el tercero, el Entscheidungsproblem, tuvo que esperar hasta mediados de la década de 1930.
El problema era que una respuesta requería primero una definición precisa de "prescripción aplicable general definida", que el profesor de Princeton Alonzo Church vendría a llamar " calculabilidad efectiva ", y en 1928 no existía tal definición. Pero durante los siguientes 6 a 7 años , Emil Post desarrolló su definición de un trabajador que se mueve de una habitación a otra escribiendo y borrando marcas según una lista de instrucciones (Post 1936), al igual que Church y sus dos estudiantes Stephen Kleene y JB Rosser mediante el uso de Cálculo lambda de Church y teoría de la recursión de Gödel (1934). El artículo de Church (publicado el 15 de abril de 1936) mostró que el Entscheidungsproblem era de hecho "indecidible" y venció a Turing por casi un año (el artículo de Turing presentado el 28 de mayo de 1936, publicado en enero de 1937). Mientras tanto, Emil Post presentó un breve artículo en el otoño de 1936, por lo que Turing al menos tenía prioridad sobre Post. Mientras Church arbitraba el artículo de Turing, Turing tuvo tiempo de estudiar el artículo de Church y agregar un Apéndice donde esbozaba una prueba de que el cálculo lambda de Church y sus máquinas calcularían las mismas funciones.
Pero lo que Church había hecho era algo bastante diferente y, en cierto sentido, más débil. ... la construcción de Turing fue más directa y proporcionó un argumento a partir de los primeros principios, cerrando la brecha en la demostración de Church.
— Hodges pág. 112
Y Post solo había propuesto una definición de calculabilidad y criticado la "definición" de Church, pero no había probado nada.
La máquina A de Alan Turing
En la primavera de 1935, Turing, como joven estudiante de maestría en King's College, Cambridge , asumió el desafío; había sido estimulado por las conferencias del lógico MHA Newman "y aprendió de ellas sobre el trabajo de Gödel y el Entscheidungsproblem ... Newman usó la palabra 'mecánico' ... En su obituario de Turing 1955 Newman escribe:
A la pregunta '¿qué es un proceso "mecánico"?' Turing devolvió la característica respuesta 'Algo que puede ser hecho por una máquina' y se embarcó en la muy agradable tarea de analizar la noción general de una máquina de computación.
— Gandy, pág. 74
Gandy afirma que:
Supongo, pero no lo sé, que Turing, desde el comienzo de su trabajo, tuvo como objetivo una prueba de la indecidibilidad del Entscheidungsproblem. Me dijo que la 'idea principal' del artículo se le ocurrió cuando yacía en los prados de Grantchester en el verano de 1935. La 'idea principal' podría haber sido su análisis de la computación o su comprensión de que había una máquina universal. , y así un argumento diagonal para probar la insolubilidad.
— ibíd. , pags. 76
Si bien Gandy creía que la declaración anterior de Newman es "engañosa", no todos comparten esta opinión. Turing tuvo un interés de por vida en las máquinas: "Alan había soñado con inventar máquinas de escribir cuando era niño; [su madre], la Sra. Turing, tenía una máquina de escribir; y bien podría haber comenzado preguntándose qué significaba llamar 'mecánica' a una máquina de escribir". (Hodges pág. 96). Mientras estaba en Princeton haciendo su doctorado, Turing construyó un multiplicador de lógica booleana (ver más abajo). Su tesis doctoral, titulada " Sistemas de lógica basados en ordinales ", contiene la siguiente definición de "función computable":
Se afirmó anteriormente que "una función es efectivamente calculable si sus valores se pueden encontrar mediante algún proceso puramente mecánico". Podemos tomar esta afirmación al pie de la letra, entendiendo por proceso puramente mecánico el que podría ser realizado por una máquina. Es posible dar una descripción matemática, en cierta forma normal, de las estructuras de estas máquinas. El desarrollo de estas ideas conduce a la definición del autor de una función computable ya una identificación de computabilidad con calculabilidad efectiva. No es difícil, aunque algo laborioso, probar que estas tres definiciones [la tercera es el cálculo λ] son equivalentes.
— Turing (1939) en El indecidible , p. 160
Alan Turing inventó la "máquina-a" (máquina automática) en 1936. Turing envió su artículo el 31 de mayo de 1936 a la Sociedad Matemática de Londres para sus Actas (cf. Hodges 1983: 112), pero se publicó a principios de 1937 y las separatas estaban disponibles en febrero de 1937 (cf. Hodges 1983: 129) Fue el asesor de doctorado de Turing, Alonzo Church , quien más tarde acuñó el término "máquina de Turing" en una revisión. Con este modelo, Turing pudo responder negativamente a dos preguntas:
- ¿Existe una máquina que pueda determinar si alguna máquina arbitraria en su cinta es "circular" (por ejemplo, se congela o no continúa con su tarea computacional)?
- ¿Existe una máquina que pueda determinar si alguna máquina arbitraria en su cinta alguna vez imprime un símbolo dado?
Por lo tanto, al proporcionar una descripción matemática de un dispositivo muy simple capaz de realizar cálculos arbitrarios, pudo probar las propiedades de la computación en general y, en particular, la incomputabilidad del Entscheidungsproblem ("problema de decisión").
Cuando Turing regresó al Reino Unido, finalmente se convirtió en el responsable conjunto de descifrar los códigos secretos alemanes creados por máquinas de encriptación llamadas "El Enigma"; también se involucró en el diseño de ACE ( Automatic Computing Engine ), "La propuesta de ACE [de Turing] era efectivamente autónoma, y sus raíces no estaban en EDVAC [la iniciativa de EE. UU.], sino en su propia máquina universal" ( Hodges pág. 318). Aún continúan los argumentos sobre el origen y la naturaleza de lo que Kleene (1952) ha denominado Tesis de Turing . Pero lo que Turing demostró con su modelo de máquina computacional aparece en su artículo " On Computable Numbers, with an Application to the Entscheidungsproblem " (1937):
[que] el problema de Hilbert Entscheidung no puede tener solución... Por lo tanto, propongo mostrar que no puede haber un proceso general para determinar si una fórmula dada U del cálculo funcional K es demostrable, es decir, que no puede haber una máquina que, suministrado con cualquier U de estas fórmulas, eventualmente dirá si U es demostrable.
— del artículo de Turing reimpreso en The Undecidable , p. 145
El ejemplo de Turing (su segunda prueba): si uno va a pedir un procedimiento general para decirnos: "¿Esta máquina alguna vez imprime 0?", la pregunta es "indecidible".
1937-1970: la "computadora digital", el nacimiento de la "ciencia de la computación"
En 1937, mientras trabajaba en Princeton en su tesis doctoral, Turing construyó un multiplicador digital (lógica booleana) desde cero, fabricando sus propios relés electromecánicos (Hodges p. 138). "La tarea de Alan era incorporar el diseño lógico de una máquina de Turing en una red de interruptores operados por relés..." (Hodges p. 138). Si bien Turing podría haber sido inicialmente curioso y experimentador, un trabajo bastante serio en la misma dirección estaba yendo en Alemania ( Konrad Zuse (1938)), y en los Estados Unidos ( Howard Aiken ) y George Stibitz (1937); los frutos de su trabajo fueron utilizados por los ejércitos del Eje y los Aliados en la Segunda Guerra Mundial (cf. Hodges p. 298–299). A principios y mediados de la década de 1950, Hao Wang y Marvin Minsky redujeron la máquina de Turing a una forma más simple (un precursor de la máquina Post-Turing de Martin Davis ); simultáneamente, los investigadores europeos estaban reduciendo la computadora electrónica novedosa a un objeto teórico similar a una computadora equivalente a lo que ahora se llama una "máquina de Turing". A fines de la década de 1950 y principios de la de 1960, los desarrollos coincidentemente paralelos de Melzak y Lambek (1961), Minsky (1961) y Shepherdson y Sturgis (1961) impulsaron el trabajo europeo más allá y redujeron la máquina de Turing a un modelo informático más amigable. modelo abstracto llamado máquina contadora ; Elgot y Robinson (1964), Hartmanis (1971), Cook y Reckhow (1973) llevaron este trabajo aún más lejos con los modelos de máquinas de registro y máquinas de acceso aleatorio, pero básicamente todas son máquinas de Turing de múltiples cintas con una instrucción similar a la aritmética. establecer.
1970-presente: como modelo de computación
Hoy en día, las máquinas de contador, registro y acceso aleatorio y su madre, la máquina de Turing, siguen siendo los modelos elegidos por los teóricos que investigan cuestiones de la teoría de la computación . En particular, la teoría de la complejidad computacional hace uso de la máquina de Turing:
Dependiendo de los objetos que a uno le guste manipular en los cálculos (números como enteros no negativos o cadenas alfanuméricas), dos modelos han obtenido una posición dominante en la teoría de la complejidad basada en máquinas:
la máquina de Turing multicinta fuera de línea ..., que representa el modelo estándar para el cálculo orientado a cadenas, y la máquina de acceso aleatorio (RAM) presentada por Cook y Reckhow ..., que modela la computadora idealizada de estilo Von Neumann.
— van Emde Boas 1990:4
Solo en el área relacionada con el análisis de algoritmos, el modelo RAM asume este papel.
— van Emde Boas 1990:16
Ver también
- jerarquía aritmética
- Atado de Bekenstein , que muestra la imposibilidad de máquinas de Turing de cinta infinita de tamaño finito y energía acotada
- BlooP y FlooP
- Constante de Chaitin u Omega (informática) para obtener información relacionada con el problema de detención
- cuarto chino
- El juego de la vida de Conway , un autómata celular completo de Turing
- Infinito digital
- La nueva mente del emperador
- Enumerador (en informática teórica)
- Genetix
- Gödel, Escher, Bach: An Eternal Golden Braid , un famoso libro que analiza, entre otros temas, la tesis de Church-Turing
- Problema de detención , para más referencias
- arquitectura de harvard
- programación imperativa
- La hormiga de Langton y Turmites , simples análogos bidimensionales de la máquina de Turing
- Lista de cosas que llevan el nombre de Alan Turing
- Arquitectura de Harvard modificada
- Máquina cuántica de Turing
- Claude Shannon , otro destacado pensador de la teoría de la información
- Ejemplos de máquinas de Turing
- interruptor de giro
- Turing tarpit , cualquier sistema informático o lenguaje que, a pesar de ser Turing completo, generalmente se considera inútil para la informática práctica
- Máquina no organizada , para las primeras ideas de Turing sobre redes neuronales
- arquitectura Von Neumann
notas
- ^ Minsky 1967: 107 "En su artículo de 1936, AM Turing definió la clase de máquinas abstractas que ahora llevan su nombre. Una máquina de Turing es una máquina de estado finito asociada con un tipo especial de entorno, su cinta, en el que puede almacenar (y luego recuperar) secuencias de símbolos", también Stone 1972: 8 donde la palabra "máquina" está entre comillas.
- ^ Stone 1972: 8 afirma "Esta "máquina" es un modelo matemático abstracto", también cf. Sipser 2006:137ff que describe el "modelo de máquina de Turing". Rogers 1987 (1967):13 se refiere a la "caracterización de Turing", Boolos Burgess y Jeffrey 2002:25 se refiere a un "tipo específico de máquina idealizada".
- ^ Sipser 2006: 137 "Una máquina de Turing puede hacer todo lo que puede hacer una computadora real".
- ^ Cf. Sipser 2002: 137. Además, Rogers 1987 (1967):13 describe "una cinta de papel de longitud infinita en ambas direcciones". Minsky 1967: 118 afirma que "la cinta se considera infinita en ambas direcciones". Boolos Burgess y Jeffrey 2002:25 incluyen la posibilidad de que "hay alguien estacionado en cada extremo para agregar cuadrados en blanco adicionales según sea necesario".
- ^ Cf. Rogers 1987 (1967): 13. Otros autores utilizan la palabra "cuadrado", por ejemplo, Boolos Burgess Jeffrey 2002:35, Minsky 1967:117, Penrose 1989:37.
- ^ Boolos Burgess Jeffry 2002:25 ilustra la máquina moviéndose a lo largo de la cinta. Penrose 1989: 36-37 se describe a sí mismo como "incómodo" con una cinta infinita y observa que "¡podría ser difícil de cambiar!"; él "prefiere pensar en la cinta como la representación de algún entorno externo a través del cual nuestro dispositivo finito puede moverse" y después de observar que el "'movimiento' es una forma conveniente de representar las cosas" y luego sugiere que "el dispositivo recibe todos su entrada de este entorno Algunas variaciones del modelo de la máquina de Turing también permiten que la cabeza permanezca en la misma posición en lugar de moverse o detenerse.
- ^ a b Hodges, Andrew (2012). Alan Turing: El Enigma (El Centenario ed.). Prensa de la Universidad de Princeton . ISBN 978-0-691-15564-7.
- ↑ La idea se le ocurrió a mediados de 1935 (quizás, vea más en la sección de Historia) después de una pregunta planteada por MHA Newman en sus conferencias: "¿Había un método definido, o como dijo Newman, un "proceso mecánico" que podría aplicarse a un enunciado matemático, y que arrojaría la respuesta de si es demostrable" (Hodges 1983:93). Turing envió su artículo el 31 de mayo de 1936 a la London Mathematical Society para sus procedimientos (cf. Hodges 1983: 112), pero se publicó a principios de 1937 y las separatas estaban disponibles en febrero de 1937 (cf. Hodges 1983: 129).
- ^ Ver nota al pie en Davis 2000:151.
- ^ véase la nota que sigue a The Collected Works of Alonzo Church ( Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church . Cambridge, MA, EE. UU.: MIT Press. ISBN 978-0-262-02564-5.)
- ^ Turing 1936 en The Undecidable 1965: 132-134; La definición de Turing de "circular" se encuentra en la página 119.
- ^ Turing, Alan Mathison (1937). "Sobre números computables, con una aplicación al Entscheidungsproblem ". Actas de la Sociedad Matemática de Londres . Serie 2. 42 (1): 230–265. doi : 10.1112/plms/s2-42.1.230 . S2CID 73712 .— Reimpresión en: Turing, Alan. "Sobre números computables, con una aplicación al Entscheidungsproblem" . El Archivo Digital de Turing . Consultado el 9 de julio de 2020 .
- ^ Turing 1936 en El indecidible 1965: 145
- ^ Sipser 2006: 137 observa que "una máquina de Turing puede hacer todo lo que puede hacer una computadora real. Sin embargo, incluso una máquina de Turing no puede resolver ciertos problemas. En un sentido muy real, estos problemas están más allá de los límites teóricos de la computación".
- ^ Consulte la definición de " entradas " en Wikcionario
- ^ AM Turing (julio de 1948). Maquinaria Inteligente (Informe). Laboratorio Nacional de Física. Aquí: p.3-4
- ^ Ocasionalmente llamada tabla de acción o función de transición .
- ^ Por lo general, quíntuples [5 tuplas]: q i a j → q i1 a j1 d k , pero a veces se cuadruplica [4 tuplas].
- ^ pág.149; en particular, Hopcroft y Ullman asumen queno está definido en todos los estados de
- ^ véase la nota que sigue a The Collected Works of Alonzo Church ( Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church . Cambridge, MA, EE. UU.: MIT Press. ISBN 978-0-262-02564-5.)
- ^ Turing 1936 en The Undecidable 1965: 132-134; La definición de Turing de "circular" se encuentra en la página 119.
- ^ Turing, Alan Mathison (1937). "Sobre números computables, con una aplicación al Entscheidungsproblem ". Actas de la Sociedad Matemática de Londres . Serie 2. 42 (1): 230–265. doi : 10.1112/plms/s2-42.1.230 . S2CID 73712 .— Reimpresión en: Turing, Alan. "Sobre números computables, con una aplicación al Entscheidungsproblem" . El Archivo Digital de Turing . Consultado el 9 de julio de 2020 .
- ^ Turing 1936 en El indecidible 1965: 145
Referencias
Literatura primaria, reimpresiones y compilaciones
- B. Jack Copeland ed. (2004), The Essential Turing: escritos seminales sobre computación, lógica, filosofía, inteligencia artificial y vida artificial más The Secrets of Enigma, Clarendon Press (Oxford University Press), Oxford Reino Unido, ISBN 0-19-825079-7 . Contiene los documentos de Turing más un borrador de carta a Emil Post sobre su crítica a la "convención de Turing" y las correcciones de Donald W. Davies a la máquina informática universal de Turing.
- Martin Davis (ed.) (1965), The Undecidable , Raven Press, Hewlett, NY.
- Emil Post (1936), "Finite Combinatory Processes—Formulation 1", Journal of Symbolic Logic , 1, 103–105, 1936. Reimpreso en The Undecidable , págs. 289 y sigs.
- Emil Post (1947), "Insolubilidad recursiva de un problema de Thue", Journal of Symbolic Logic , vol. 12, págs. 1–11. Reimpreso en The Undecidable , pp. 293ff. En el Apéndice de este artículo, Post comenta y corrige el artículo de Turing de 1936–1937. En particular, véanse las notas a pie de página 11 con correcciones a la codificación de la máquina informática universal y la nota a pie de página 14 con comentarios sobre la primera y segunda prueba de Turing .
- Turing, AM (1936). "Sobre números computables, con una aplicación al Entscheidungsproblem". Actas de la Sociedad Matemática de Londres . 2 (publicado en 1937). 42 : 230–265. doi : 10.1112/plms/s2-42.1.230 . S2CID 73712 .(y Turing, AM (1938). "Sobre números computables, con una aplicación al problema Entscheidungs: una corrección". Actas de la London Mathematical Society . 2 (publicado en 1937). 43 (6): 544–6. doi : 10.1112 /plms/s2-43.6.544 .). Reimpreso en muchas colecciones, por ejemplo, en The Undecidable , págs. 115–154; disponible en la web en muchos lugares.
- Alan Turing, 1948, "Maquinaria inteligente". Reimpreso en "Cybernetics: Key Papers". ed. CR Evans y ADJ Robertson. Baltimore: University Park Press, 1968. pág. 31. Reimpreso en Turing, AM (1996). "Maquinaria inteligente, una teoría herética". Filosofía Matemática . 4 (3): 256–260. doi : 10.1093/philmat/4.3.256 .
- FC Hennie y RE Stearns . Simulación de dos cintas de máquinas de Turing multicinta . JACM , 13(4):533–546, 1966.
teoría de la computabilidad
- Boolos, Jorge; Richard Jeffrey (1999) [1989]. Computabilidad y lógica (3ª ed.). Cambridge Reino Unido: Cambridge University Press. ISBN 0-521-20402-X.
- Boolos, Jorge; Juan Burgess; Richard Jeffrey (2002). Computabilidad y Lógica (4ª ed.). Cambridge Reino Unido: Cambridge University Press. ISBN 0-521-00758-5.Burgess ha reescrito significativamente algunas partes. Presentación de las máquinas de Turing en el contexto de las "máquinas de ábaco" de Lambek (cf. Máquina de registro ) y funciones recursivas , mostrando su equivalencia.
- Taylor L. Booth (1967), Máquinas secuenciales y teoría de autómatas , John Wiley and Sons, Inc., Nueva York. Texto de ingeniería de nivel de posgrado; cubre una amplia variedad de temas, el Capítulo IX Máquinas de Turing incluye algo de teoría de la recursión.
- Martín Davis (1958). Computabilidad e insolubilidad . McGraw-Hill Book Company, Inc., Nueva York.. En las páginas 12 a 20, ofrece ejemplos de tablas de 5 tuplas para la suma, la función sucesora, la resta (x ≥ y), la resta propia (0 si x < y), la función de identidad y varias funciones de identidad, y la multiplicación.
- Davis, Martín; Ron Sigal; Elaine J. Weyuker (1994). Computabilidad, complejidad y lenguajes y lógica: fundamentos de la informática teórica (2ª ed.). San Diego: Prensa Académica, Harcourt, Brace & Company. ISBN 0-12-206382-1.
- Hennie, Fredrick (1977). Introducción a la Computabilidad . Addison–Wesley, Reading, Massachusetts QA248.5H4 1977.. En las páginas 90 a 103, Hennie analiza el UTM con ejemplos y diagramas de flujo, pero sin un "código" real.
- John Hopcroft y Jeffrey Ullman (1979). Introducción a la teoría, los lenguajes y la computación de los autómatas (1.ª ed.). Addison-Wesley, Reading Mass. ISBN 0-201-02988-X.Centrado en los problemas de interpretación automática de "lenguajes", integridad de NP, etc.
- Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). Introducción a la teoría de autómatas, lenguajes y computación (2ª ed.). Misa de lectura: Addison–Wesley. ISBN 0-201-44124-1.
- Stephen Kleene (1952), Introduction to Metamathematics , North–Holland Publishing Company, Ámsterdam, Países Bajos, décima impresión (con correcciones de la sexta reimpresión, 1971). Texto de nivel de posgrado; la mayor parte del Capítulo XIII Funciones computables se trata de pruebas de máquina de Turing de computabilidad de funciones recursivas, etc.
- Knuth, Donald E. (1973). Volumen 1/Algoritmos fundamentales: El arte de la programación informática (2ª ed.). Reading, Mass.: Addison–Wesley Publishing Company.. Con referencia al papel de las máquinas de Turing en el desarrollo de la computación (tanto hardware como software), véase 1.4.5 Historia y bibliografía , págs. 225 y siguientes, y 2.6 Historia y bibliografía , págs. 456 y siguientes.
- Zohar Manna , 1974, Teoría matemática de la computación . Reimpreso, Dover, 2003. ISBN 978-0-486-43238-0
- Marvin Minsky , Computation: Finite and Infinite Machines , Prentice–Hall, Inc., NJ, 1967. Consulte el Capítulo 8, Sección 8.2, "Insolubilidad del problema de detención".
- Christos Papadimitriou (1993). Complejidad computacional (1ª ed.). AddisonWesley. ISBN 0-201-53082-1.Capítulo 2: Máquinas de Turing, págs. 19–56.
- Hartley Rogers, Jr. , Teoría de funciones recursivas y computabilidad efectiva , The MIT Press, Cambridge MA, edición de bolsillo de 1987, edición original de McGraw-Hill de 1967, ISBN 0-262-68052-1 (pbk.)
- Michael Sipser (1997). Introducción a la Teoría de la Computación . Editorial PWS. ISBN 0-534-94728-X.Capítulo 3: La tesis de Church–Turing, págs. 125–149.
- Piedra, Harold S. (1972). Introducción a la organización informática y estructuras de datos (1ª ed.). Nueva York: McGraw–Hill Book Company. ISBN 0-07-061726-0.
- Peter van Emde Boas 1990, Machine Models and Simulations , págs. 3–66, en Jan van Leeuwen , ed., Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity , The MIT Press/Elsevier, [¿lugar?], ISBN 0-444-88071-2 (Tomo A). QA76.H279 1990.
la tesis de la iglesia
- Nachum Dershowitz; Yuri Gurevich (septiembre de 2008). "Una axiomatización natural de la computabilidad y prueba de la tesis de Church" (PDF) . Boletín de Lógica Simbólica . 14 (3) . Consultado el 15 de octubre de 2008 .
- Roger Penrose (1990) [1989]. La nueva mente del emperador (2ª ed.). Prensa de la Universidad de Oxford, Nueva York. ISBN 0-19-851973-7.
Pequeñas máquinas de Turing
- Rogozhin, Yurii, 1998, " A Universal Turing Machine with 22 States and 2 Symbols ", Romanian Journal of Information Science and Technology , 1(3), 259–265, 1998. (resultados conocidos de encuestas sobre pequeñas máquinas universales de Turing)
- Stephen Wolfram , 2002, Un nuevo tipo de ciencia , Wolfram Media, ISBN 1-57955-008-8
- Brunfiel, Geoff, Student snags maths Prize , Nature , 24 de octubre de 2007.
- Jim Giles (2007), La 'computadora universal' más simple gana $ 25,000 para estudiantes , New Scientist, 24 de octubre de 2007.
- Alex Smith, Universalidad de la máquina de Turing 2, 3 de Wolfram , presentación para el premio de investigación de la máquina de Turing Wolfram 2, 3.
- Vaughan Pratt, 2007, " Máquinas de Turing simples, universalidad, codificaciones, etc. ", lista de correo electrónico de FOM. 29 de octubre de 2007.
- Martin Davis, 2007, " La máquina universal más pequeña " y Definición de la lista de correo electrónico FOM de la máquina de Turing universal . 26 y 27 de octubre de 2007.
- Alasdair Urquhart, 2007 " La máquina universal más pequeña ", lista de correo electrónico de FOM. 26 de octubre de 2007.
- Hector Zenil (Wolfram Research), 2007 " máquina universal más pequeña ", lista de correo electrónico de FOM. 29 de octubre de 2007.
- Todd Rowland, 2007, " Confusion on FOM ", tablero de mensajes de Wolfram Science, 30 de octubre de 2007.
- Olivier y Marc RAYNAUD, 2014, Un prototipo programable para lograr máquinas de Turing " Laboratorio LIMOS de la Universidad Blaise Pascal (Clermont-Ferrand en Francia).
Otro
- Martín Davis (2000). Motores de lógica: matemáticos y el origen de la computadora (1ª ed.). WW Norton & Company, Nueva York. ISBN 978-0-393-32229-3.
- Robin Gandy , "La confluencia de ideas en 1936", págs. 51–102 en Rolf Herken , ver más abajo.
- Stephen Hawking (editor), 2005, Dios creó los números enteros: los avances matemáticos que cambiaron la historia , Running Press, Filadelfia, ISBN 978-0-7624-1922-7 . Incluye el artículo de Turing de 1936–1937, con un breve comentario y una biografía de Turing escrita por Hawking.
- Rolf Herken (1995). La máquina universal de Turing: una encuesta de medio siglo . Springer Verlag. ISBN 978-3-211-82637-9.
- Andrew Hodges , Alan Turing: El Enigma , Simon and Schuster , Nueva York. Cf. Capítulo "El espíritu de la verdad" para una historia que lleva a su prueba y una discusión sobre ella.
- Ivars Peterson (1988). El turista matemático: instantáneas de las matemáticas modernas (1ª ed.). WH Freeman and Company, Nueva York. ISBN 978-0-7167-2064-5.
- Roger Penrose , The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics , Oxford University Press , Oxford y Nueva York, 1989 (correcciones de 1990), ISBN 0-19-851973-7 .
- Paul Strathern (1997). Turing y la computadora: la gran idea . Libros de anclaje/Doubleday. ISBN 978-0-385-49243-0.
- Hao Wang , "Una variante de la teoría de las máquinas informáticas de Turing", Revista de la Asociación de Maquinaria Informática (JACM) 4, 63–92 (1957).
- Charles Petzold , Petzold, Charles, El Turing anotado , John Wiley & Sons, Inc., ISBN 0-470-22905-5
- Arora, Sanjeev; Barak, Boaz, "Teoría de la complejidad: un enfoque moderno" , Cambridge University Press, 2009, ISBN 978-0-521-42426-4 , sección 1.4, "Máquinas como cuerdas y la máquina de Turing universal" y 1.7, "Prueba del teorema 1,9"
- Kantorovitz, Isaiah Pinchas (1 de diciembre de 2005). "Una nota sobre la computabilidad de la máquina de Turing de los sistemas controlados por reglas". Noticias SIGACT . 36 (4): 109–110. doi : 10.1145/1107523.1107525 . S2CID 31117713 .
- Kirner, Raimund; Zimmermann, Lobo; Richter, Dirk: "Sobre los resultados de indecidibilidad de los lenguajes de programación reales" , en 15. Kolloquium Programmiersprachen und Grundlagen der Programmierung (KPS'09), Maria Taferl, Austria, octubre de 2009.
enlaces externos
- "Máquina de Turing" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Máquina de Turing en la Enciclopedia de Filosofía de Stanford
- Turing Machine Causal Networks por Enrique Zeleny como parte del Wolfram Demonstrations Project .
- Máquinas de Turing en Curlie