Red de función de base radial - Radial basis function network

En el campo del modelado matemático , una red de función de base radial es una red neuronal artificial que utiliza funciones de base radial como funciones de activación . La salida de la red es una combinación lineal de funciones de base radial de las entradas y los parámetros neuronales. Las redes de funciones de base radial tienen muchos usos, incluida la aproximación de funciones , la predicción de series de tiempo , la clasificación y el control del sistema . Fueron formulados por primera vez en un artículo de 1988 por Broomhead y Lowe, ambos investigadores de Royal Signals y Radar Establishment .

Red de arquitectura

Arquitectura de una red de funciones de base radial. Un vector de entrada se utiliza como entrada para todas las funciones de base radial, cada una con diferentes parámetros. La salida de la red es una combinación lineal de las salidas de las funciones de base radial.${\ Displaystyle x}$

Las redes de función de base radial (RBF) suelen tener tres capas: una capa de entrada, una capa oculta con una función de activación de RBF no lineal y una capa de salida lineal. La entrada se puede modelar como un vector de números reales . La salida de la red es entonces una función escalar del vector de entrada , y viene dada por ${\ Displaystyle \ mathbf {x} \ in \ mathbb {R} ^ {n}}$${\ Displaystyle \ varphi: \ mathbb {R} ^ {n} \ to \ mathbb {R}}$

${\ Displaystyle \ varphi (\ mathbf {x}) = \ sum _ {i = 1} ^ {N} a_ {i} \ rho (|| \ mathbf {x} - \ mathbf {c} _ {i} | |)}$

donde es el número de neuronas en la capa oculta, es el vector central de la neurona y es el peso de la neurona en la neurona de salida lineal. Las funciones que dependen solo de la distancia desde un vector central son radialmente simétricas con respecto a ese vector, de ahí el nombre de función de base radial. En la forma básica, todas las entradas están conectadas a cada neurona oculta. Por lo general, se considera que la norma es la distancia euclidiana (aunque la distancia de Mahalanobis parece funcionar mejor con el reconocimiento de patrones) y la función de base radial se considera comúnmente gaussiana.${\ Displaystyle N}$${\ Displaystyle \ mathbf {c} _ {i}}$${\ Displaystyle i}$${\ Displaystyle a_ {i}}$${\ Displaystyle i}$

${\ Displaystyle \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} = \ exp \ left [- \ beta _ {i } \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert ^ {2} \ right]}$.

Las funciones de base de Gauss son locales al vector central en el sentido de que

${\ Displaystyle \ lim _ {|| x || \ to \ infty} \ rho (\ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert) = 0}$

es decir, cambiar los parámetros de una neurona sólo tiene un pequeño efecto para los valores de entrada que están lejos del centro de esa neurona.

Dadas ciertas condiciones suaves en la forma de la función de activación, las redes RBF son aproximadores universales en un subconjunto compacto de . Esto significa que una red RBF con suficientes neuronas ocultas puede aproximarse a cualquier función continua en un conjunto cerrado y acotado con precisión arbitraria. ${\ Displaystyle \ mathbb {R} ^ {n}}$

Los parámetros , y se determinan de una manera que optimiza el ajuste entre y los datos. ${\ Displaystyle a_ {i}}$${\ Displaystyle \ mathbf {c} _ {i}}$${\ Displaystyle \ beta _ {i}}$${\ Displaystyle \ varphi}$

Dos funciones de base radial no normalizadas en una dimensión de entrada. Los centros de funciones básicos se encuentran en y .${\ Displaystyle c_ {1} = 0,75}$${\ Displaystyle c_ {2} = 3,25}$

Normalizado

Dos funciones de base radial normalizadas en una dimensión de entrada ( sigmoides ). Los centros de funciones básicos se encuentran en y .${\ Displaystyle c_ {1} = 0,75}$${\ Displaystyle c_ {2} = 3,25}$

Tres funciones de base radial normalizadas en una dimensión de entrada. La función de base adicional tiene el centro en${\ Displaystyle c_ {3} = 2,75}$

Cuatro funciones de base radial normalizadas en una dimensión de entrada. La cuarta función de base tiene centro en . Tenga en cuenta que la primera función de base (azul oscuro) se ha localizado.${\ Displaystyle c_ {4} = 0}$

Arquitectura normalizada

Además de la arquitectura no normalizada anterior , las redes RBF se pueden normalizar . En este caso, el mapeo es

${\ Displaystyle \ varphi (\ mathbf {x}) \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ sum _ {i = 1} ^ {N} a_ {i} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho { \ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}} = \ sum _ {i = 1} ^ {N} a_ {i } u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

dónde

${\ Displaystyle u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} \ {\ stackrel {\ mathrm {def}} {= }} \ {\ frac {\ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {j = 1} ^ {N} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {j} \ right \ Vert {\ big)}}}}$

se conoce como función de base radial normalizada .

Motivación teórica para la normalización

Existe una justificación teórica para esta arquitectura en el caso del flujo de datos estocástico. Suponga una aproximación de kernel estocástica para la densidad de probabilidad conjunta

${\ Displaystyle P \ left (\ mathbf {x} \ land y \ right) = {1 \ over N} \ sum _ {i = 1} ^ {N} \, \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} \, \ sigma {\ big (} \ left \ vert y-e_ {i} \ right \ vert {\ big )}}$

donde los pesos y son ejemplos de los datos y requerimos que los núcleos estén normalizados ${\ Displaystyle \ mathbf {c} _ {i}}$${\ Displaystyle e_ {i}}$

${\ Displaystyle \ int \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} \, d ^ {n} \ mathbf { x} = 1}$

y

${\ Displaystyle \ int \ sigma {\ big (} \ left \ vert y-e_ {i} \ right \ vert {\ big)} \, dy = 1}$.

Las densidades de probabilidad en los espacios de entrada y salida son

${\ Displaystyle P \ left (\ mathbf {x} \ right) = \ int P \ left (\ mathbf {x} \ land y \ right) \, dy = {1 \ over N} \ sum _ {i = 1 } ^ {N} \, \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

y

La expectativa de y dada una entrada es ${\ Displaystyle \ mathbf {x}}$

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) \ {\ stackrel {\ mathrm {def}} {=}} \ E \ left (y \ mid \ mathbf {x} \ right) = \ int y \, P \ left (y \ mid \ mathbf {x} \ right) dy}$

dónde

${\ Displaystyle P \ left (y \ mid \ mathbf {x} \ right)}$

es la probabilidad condicional de y dada . La probabilidad condicional está relacionada con la probabilidad conjunta a través del teorema de Bayes.${\ Displaystyle \ mathbf {x}}$

${\ Displaystyle P \ left (y \ mid \ mathbf {x} \ right) = {\ frac {P \ left (\ mathbf {x} \ land y \ right)} {P \ left (\ mathbf {x} \ derecho)}}}$

cuyos rendimientos

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) = \ int y \, {\ frac {P \ left (\ mathbf {x} \ land y \ right)} {P \ left (\ mathbf { x} \ right)}} \, dy}$.

Esto se convierte en

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) = {\ frac {\ sum _ {i = 1} ^ {N} e_ {i} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho {\ big (} \ left \ Vert \ mathbf { x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}} = \ sum _ {i = 1} ^ {N} e_ {i} u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

cuando se realizan las integraciones.

Modelos lineales locales

A veces es conveniente expandir la arquitectura para incluir modelos lineales locales . En ese caso las arquitecturas se vuelven, de primer orden,

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) = \ sum _ {i = 1} ^ {N} \ left (a_ {i} + \ mathbf {b} _ {i} \ cdot \ left (\ mathbf {x} - \ mathbf {c} _ {i} \ right) \ right) \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

y

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) = \ sum _ {i = 1} ^ {N} \ left (a_ {i} + \ mathbf {b} _ {i} \ cdot \ left (\ mathbf {x} - \ mathbf {c} _ {i} \ right) \ right) u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

en los casos normalizados y no normalizados, respectivamente. Aquí están los pesos por determinar. También son posibles términos lineales de orden superior. ${\ Displaystyle \ mathbf {b} _ {i}}$

Este resultado se puede escribir

${\ Displaystyle \ varphi \ left (\ mathbf {x} \ right) = \ sum _ {i = 1} ^ {2N} \ sum _ {j = 1} ^ {n} e_ {ij} v_ {ij} { \ big (} \ mathbf {x} - \ mathbf {c} _ {i} {\ big)}}$

dónde

${\ displaystyle e_ {ij} = {\ begin {cases} a_ {i}, & {\ mbox {if}} i \ in [1, N] \\ b_ {ij}, & {\ mbox {if}} i \ in [N + 1,2N] \ end {cases}}}$

y

${\ Displaystyle v_ {ij} {\ big (} \ mathbf {x} - \ mathbf {c} _ {i} {\ big)} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ comenzar {casos} \ delta _ {ij} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}, & {\ mbox {if}} i \ in [1, N] \\\ left (x_ {ij} -c_ {ij} \ right) \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c } _ {i} \ right \ Vert {\ big)}, & {\ mbox {if}} i \ en [N + 1,2N] \ end {cases}}}$

en el caso no normalizado y

${\ Displaystyle v_ {ij} {\ big (} \ mathbf {x} - \ mathbf {c} _ {i} {\ big)} \ {\ stackrel {\ mathrm {def}} {=}} \ {\ comenzar {casos} \ delta _ {ij} u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}, & {\ mbox { if}} i \ in [1, N] \\\ left (x_ {ij} -c_ {ij} \ right) u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}, & {\ mbox {if}} i \ en [N + 1,2N] \ end {cases}}}$

en el caso normalizado.

Aquí hay una función delta de Kronecker definida como ${\ Displaystyle \ delta _ {ij}}$

${\ Displaystyle \ delta _ {ij} = {\ begin {cases} 1, & {\ mbox {if}} i = j \\ 0, & {\ mbox {if}} i \ neq j \ end {cases} }}$.

Capacitación

Las redes RBF generalmente se entrenan a partir de pares de valores de entrada y de destino , mediante un algoritmo de dos pasos. ${\ Displaystyle \ mathbf {x} (t), y (t)}$${\ Displaystyle t = 1, \ dots, T}$

En el primer paso, se eligen los vectores centrales de las funciones RBF en la capa oculta. Este paso se puede realizar de varias formas; los centros se pueden muestrear aleatoriamente a partir de algún conjunto de ejemplos, o se pueden determinar mediante la agrupación de k-medias . Tenga en cuenta que este paso no está supervisado . ${\ Displaystyle \ mathbf {c} _ {i}}$

El segundo paso simplemente ajusta un modelo lineal con coeficientes a las salidas de la capa oculta con respecto a alguna función objetivo. Una función objetivo común, al menos para la estimación de regresión / función, es la función de mínimos cuadrados: ${\ Displaystyle w_ {i}}$

${\ Displaystyle K (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ \ sum _ {t = 1} ^ {T} K_ {t} (\ mathbf {w}) }$

dónde

${\ Displaystyle K_ {t} (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ {\ big [} y (t) - \ varphi {\ big (} \ mathbf { x} (t), \ mathbf {w} {\ big)} {\ big]} ^ {2}}$.

Hemos incluido explícitamente la dependencia de los pesos. La minimización de la función objetivo de mínimos cuadrados mediante la elección óptima de pesos optimiza la precisión del ajuste.

Hay ocasiones en las que se deben optimizar múltiples objetivos, como la suavidad y la precisión. En ese caso, es útil optimizar una función objetivo regularizada como

${\ Displaystyle H (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ K (\ mathbf {w}) + \ lambda S (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ \ sum _ {t = 1} ^ {T} H_ {t} (\ mathbf {w})}$

dónde

${\ Displaystyle S (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ \ sum _ {t = 1} ^ {T} S_ {t} (\ mathbf {w}) }$

y

${\ Displaystyle H_ {t} (\ mathbf {w}) \ {\ stackrel {\ mathrm {def}} {=}} \ K_ {t} (\ mathbf {w}) + \ lambda S_ {t} (\ mathbf {w})}$

donde la optimización de S maximiza la suavidad y se conoce como parámetro de regularización . ${\ Displaystyle \ lambda}$

Se puede realizar un tercer paso de retropropagación opcional para ajustar todos los parámetros de la red RBF.

Interpolación

Redes RBF se pueden utilizar para interpolar una función cuando se conocen los valores de esa función en número finito de puntos: . Tomando los puntos conocidos como los centros de las funciones de base radial y evaluando los valores de las funciones de base en los mismos puntos, los pesos se pueden resolver a partir de la ecuación ${\ Displaystyle y: \ mathbb {R} ^ {n} \ to \ mathbb {R}}$${\ Displaystyle y (\ mathbf {x} _ {i}) = b_ {i}, i = 1, \ ldots, N}$${\ Displaystyle \ mathbf {x} _ {i}}$${\ Displaystyle g_ {ij} = \ rho (|| \ mathbf {x} _ {j} - \ mathbf {x} _ {i} ||)}$

${\ Displaystyle \ left [{\ begin {matrix} g_ {11} & g_ {12} & \ cdots & g_ {1N} \\ g_ {21} & g_ {22} & \ cdots & g_ {2N} \\\ vdots && \ " ddots & \ vdots \\ g_ {N1} & g_ {N2} & \ cdots & g_ {NN} \ end {matrix}} \ right] \ left [{\ begin {matrix} w_ {1} \\ w_ {2} \ \\ vdots \\ w_ {N} \ end {matriz}} \ right] = \ left [{\ begin {matrix} b_ {1} \\ b_ {2} \\\ vdots \\ b_ {N} \ end {matriz}} \ derecha]}$

Se puede demostrar que la matriz de interpolación en la ecuación anterior no es singular, si los puntos son distintos y, por lo tanto, los pesos se pueden resolver mediante álgebra lineal simple: ${\ Displaystyle \ mathbf {x} _ {i}}$${\ Displaystyle w}$

${\ Displaystyle \ mathbf {w} = \ mathbf {G} ^ {- 1} \ mathbf {b}}$

donde . ${\ Displaystyle G = (g_ {ij})}$

Aproximación de funciones

Si el propósito no es realizar una interpolación estricta, sino una aproximación o clasificación de funciones más generales , la optimización es algo más compleja porque no hay una opción obvia para los centros. El entrenamiento generalmente se realiza en dos fases, primero fijando el ancho y los centros y luego los pesos. Esto puede justificarse considerando la naturaleza diferente de las neuronas ocultas no lineales frente a la neurona de salida lineal.

Formación de los centros de funciones base

Los centros de función básica se pueden muestrear aleatoriamente entre las instancias de entrada o se pueden obtener mediante el algoritmo de aprendizaje de mínimos cuadrados ortogonales o se pueden encontrar agrupando las muestras y eligiendo las medias del grupo como centros.

Los anchos de RBF generalmente se fijan todos al mismo valor que es proporcional a la distancia máxima entre los centros elegidos.

Solución pseudoinversa para los pesos lineales

Una vez que se han fijado los centros , las ponderaciones que minimizan el error en la salida se pueden calcular con una solución lineal pseudoinversa : ${\ Displaystyle c_ {i}}$

${\ Displaystyle \ mathbf {w} = \ mathbf {G} ^ {+} \ mathbf {b}}$,

donde las entradas de G son los valores de las funciones de base radial evaluados en los puntos de : . ${\ Displaystyle x_ {i}}$${\ Displaystyle g_ {ji} = \ rho (|| x_ {j} -c_ {i} ||)}$

La existencia de esta solución lineal significa que, a diferencia de las redes de perceptrones multicapa (MLP), las redes RBF tienen un minimizador explícito (cuando los centros son fijos).

Entrenamiento de descenso de gradiente de los pesos lineales

Otro posible algoritmo de entrenamiento es el descenso de gradientes . En el entrenamiento de descenso de gradiente, los pesos se ajustan en cada paso de tiempo moviéndolos en una dirección opuesta al gradiente de la función objetivo (permitiendo así encontrar el mínimo de la función objetivo),

${\ Displaystyle \ mathbf {w} (t + 1) = \ mathbf {w} (t) - \ nu {\ frac {d} {d \ mathbf {w}}} H_ {t} (\ mathbf {w} )}$

donde es un "parámetro de aprendizaje". ${\ Displaystyle \ nu}$

Para el caso de entrenar los pesos lineales , el algoritmo se convierte en ${\ Displaystyle a_ {i}}$

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} \ rho {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big )}}$

en el caso no normalizado y

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} u {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big) }}$

en el caso normalizado.

Para arquitecturas lineales locales, el entrenamiento de descenso de gradientes es

${\ Displaystyle e_ {ij} (t + 1) = e_ {ij} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} v_ {ij} {\ big (} \ mathbf {x} (t) - \ mathbf {c} _ {i} {\ big)}}$

Entrenamiento del operador de proyección de los pesos lineales

Para el caso de entrenar los pesos lineales, y , el algoritmo se convierte en ${\ Displaystyle a_ {i}}$${\ Displaystyle e_ {ij}}$

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} {\ frac {\ rho {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho ^ {2} {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}}}$

en el caso no normalizado y

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} {\ frac {u {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} u ^ {2} {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i } \ right \ Vert {\ big)}}}}$

en el caso normalizado y

${\ Displaystyle e_ {ij} (t + 1) = e_ {ij} (t) + \ nu {\ big [} y (t) - \ varphi {\ big (} \ mathbf {x} (t), \ mathbf {w} {\ big)} {\ big]} {\ frac {v_ {ij} {\ big (} \ mathbf {x} (t) - \ mathbf {c} _ {i} {\ big)} } {\ sum _ {i = 1} ^ {N} \ sum _ {j = 1} ^ {n} v_ {ij} ^ {2} {\ big (} \ mathbf {x} (t) - \ mathbf {c} _ {i} {\ big)}}}}$

en el caso local-lineal.

Para una función básica, el entrenamiento del operador de proyección se reduce al método de Newton .

Figura 6: Serie temporal del mapa logístico. La iteración repetida del mapa logístico genera una serie de tiempo caótica. Los valores se encuentran entre cero y uno. Aquí se muestran los 100 puntos de entrenamiento utilizados para entrenar los ejemplos de esta sección. Los pesos c son los primeros cinco puntos de esta serie de tiempo.

Ejemplos de

Mapa logístico

Las propiedades básicas de las funciones de base radial se pueden ilustrar con un mapa matemático simple, el mapa logístico , que mapea el intervalo unitario sobre sí mismo. Se puede utilizar para generar un prototipo de flujo de datos conveniente. El mapa logístico se puede utilizar para explorar la aproximación de funciones , la predicción de series de tiempo y la teoría de control . El mapa se originó en el campo de la dinámica de poblaciones y se convirtió en el prototipo de series de tiempo caóticas . El mapa, en el régimen completamente caótico, está dado por

${\ Displaystyle x (t + 1) \ {\ stackrel {\ mathrm {def}} {=}} \ f \ left [x (t) \ right] = 4x (t) \ left [1-x (t) \derecho]}$

donde t es un índice de tiempo. El valor de x en el tiempo t + 1 es una función parabólica de x en el tiempo t. Esta ecuación representa la geometría subyacente de la caótica serie temporal generada por el mapa logístico.

La generación de la serie de tiempo a partir de esta ecuación es el problema hacia adelante . Los ejemplos aquí ilustran el problema inverso ; identificación de la dinámica subyacente, o ecuación fundamental, del mapa logístico a partir de ejemplos de la serie temporal. El objetivo es encontrar una estimación

${\ Displaystyle x (t + 1) = f \ left [x (t) \ right] \ approx \ varphi (t) = \ varphi \ left [x (t) \ right]}$

para f.

Aproximación de funciones

Funciones de base radial no normalizadas

La arquitectura es

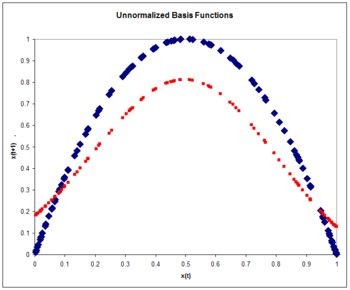
Figura 7: Funciones de base no normalizadas. El mapa logístico (azul) y la aproximación al mapa logístico (rojo) después de una pasada por el conjunto de entrenamiento.

${\ Displaystyle \ varphi (\ mathbf {x}) \ {\ stackrel {\ mathrm {def}} {=}} \ \ sum _ {i = 1} ^ {N} a_ {i} \ rho {\ big ( } \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

dónde

${\ Displaystyle \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} = \ exp \ left [- \ beta _ {i } \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert ^ {2} \ right] = \ exp \ left [- \ beta _ {i} \ left (x (t ) -c_ {i} \ right) ^ {2} \ right]}$.

Dado que la entrada es un escalar en lugar de un vector , la dimensión de entrada es uno. Elegimos el número de funciones de base como N = 5 y el tamaño del conjunto de entrenamiento para ser 100 ejemplos generados por la serie de tiempo caótica. El peso se considera una constante igual a 5. Los pesos son cinco ejemplos de la serie de tiempo. Los pesos se entrenan con la formación del operador de proyección: ${\ Displaystyle \ beta}$${\ Displaystyle c_ {i}}$${\ Displaystyle a_ {i}}$

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} x (t + 1) - \ varphi {\ big (} \ mathbf {x} (t) , \ mathbf {w} {\ big)} {\ big]} {\ frac {\ rho {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ derecha \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho ^ {2} {\ big (} \ izquierda \ Vert \ mathbf {x} (t) - \ mathbf {c } _ {i} \ right \ Vert {\ big)}}}}$

donde la tasa de aprendizaje se considera 0,3. El entrenamiento se realiza con una pasada por los 100 puntos de entrenamiento. El error rms es 0,15. ${\ Displaystyle \ nu}$

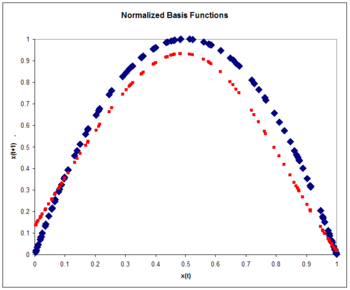
Figura 8: Funciones de base normalizadas. El mapa logístico (azul) y la aproximación al mapa logístico (rojo) después de una pasada por el conjunto de entrenamiento. Tenga en cuenta la mejora con respecto al caso no normalizado.

Funciones de base radial normalizadas

La arquitectura RBF normalizada es

${\ Displaystyle \ varphi (\ mathbf {x}) \ {\ stackrel {\ mathrm {def}} {=}} \ {\ frac {\ sum _ {i = 1} ^ {N} a_ {i} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho { \ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}} = \ sum _ {i = 1} ^ {N} a_ {i } u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}$

dónde

${\ Displaystyle u {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} \ {\ stackrel {\ mathrm {def}} {= }} \ {\ frac {\ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}}}$.

De nuevo:

${\ Displaystyle \ rho {\ big (} \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert {\ big)} = \ exp \ left [- \ beta \ left \ Vert \ mathbf {x} - \ mathbf {c} _ {i} \ right \ Vert ^ {2} \ right] = \ exp \ left [- \ beta \ left (x (t) -c_ {i} \ right ) ^ {2} \ right]}$.

Nuevamente, elegimos el número de funciones base como cinco y el tamaño del conjunto de entrenamiento para ser 100 ejemplos generados por la serie de tiempo caótica. El peso se considera una constante igual a 6. Los pesos son cinco ejemplos de la serie temporal. Los pesos se entrenan con la formación del operador de proyección: ${\ Displaystyle \ beta}$${\ Displaystyle c_ {i}}$${\ Displaystyle a_ {i}}$

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu {\ big [} x (t + 1) - \ varphi {\ big (} \ mathbf {x} (t) , \ mathbf {w} {\ big)} {\ big]} {\ frac {u {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} u ^ {2} {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}}}$

donde la tasa de aprendizaje se toma nuevamente como 0.3. El entrenamiento se realiza con una pasada por los 100 puntos de entrenamiento. El error rms en un conjunto de prueba de 100 ejemplares es 0.084, menor que el error no normalizado. La normalización produce una mejora de la precisión. Normalmente, la precisión con funciones de base normalizadas aumenta aún más que las funciones no normalizadas a medida que aumenta la dimensionalidad de entrada. ${\ Displaystyle \ nu}$

Figura 9: Funciones de base normalizadas. El mapa logístico (azul) y la aproximación al mapa logístico (rojo) en función del tiempo. Tenga en cuenta que la aproximación es válida solo para unos pocos pasos de tiempo. Ésta es una característica general de las series temporales caóticas.

Predicción de series de tiempo

Una vez que se estima la geometría subyacente de la serie de tiempo como en los ejemplos anteriores, se puede hacer una predicción para la serie de tiempo por iteración:

${\ Displaystyle \ varphi (0) = x (1)}$

${\ Displaystyle {x} (t) \ approx \ varphi (t-1)}$

${\ Displaystyle {x} (t ​​+ 1) \ approx \ varphi (t) = \ varphi [\ varphi (t-1)]}$.

En la figura se muestra una comparación de las series de tiempo real y estimada. La serie de tiempos estimada comienza en el tiempo cero con un conocimiento exacto de x (0). A continuación, utiliza la estimación de la dinámica para actualizar la estimación de la serie de tiempo para varios pasos de tiempo.

Tenga en cuenta que la estimación es precisa solo para unos pocos pasos de tiempo. Ésta es una característica general de las series temporales caóticas. Ésta es una propiedad de la dependencia sensible de las condiciones iniciales comunes a las series de tiempo caóticas. Un pequeño error inicial se amplifica con el tiempo. Una medida de la divergencia de series de tiempo con condiciones iniciales casi idénticas se conoce como exponente de Lyapunov .

Control de una serie temporal caótica

Figura 10: Control del mapa logístico. Se permite que el sistema evolucione de forma natural durante 49 pasos de tiempo. En el momento 50 se enciende el control. La trayectoria deseada para la serie temporal es roja. El sistema bajo control aprende la dinámica subyacente y conduce la serie de tiempo a la salida deseada. La arquitectura es la misma que para el ejemplo de predicción de series de tiempo.

Suponemos que la salida del mapa logístico se puede manipular a través de un parámetro de control tal que ${\ Displaystyle c [x (t), t]}$

${\ Displaystyle {x} _ {} ^ {} (t + 1) = 4x (t) [1-x (t)] + c [x (t), t]}$.

El objetivo es elegir el parámetro de control de tal manera que lleve la serie de tiempo a una salida deseada . Esto se puede hacer si elegimos el parámetro de control para ser ${\ Displaystyle d (t)}$

${\ Displaystyle c _ {} ^ {} [x (t), t] \ {\ stackrel {\ mathrm {def}} {=}} \ - \ varphi [x (t)] + d (t + 1)}$

dónde

${\ Displaystyle y [x (t)] \ approx f [x (t)] = x (t + 1) -c [x (t), t]}$

es una aproximación a la dinámica natural subyacente del sistema.

El algoritmo de aprendizaje viene dado por

${\ Displaystyle a_ {i} (t + 1) = a_ {i} (t) + \ nu \ varepsilon {\ frac {u {\ big (} \ left \ Vert \ mathbf {x} (t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}} {\ sum _ {i = 1} ^ {N} u ^ {2} {\ big (} \ left \ Vert \ mathbf {x} ( t) - \ mathbf {c} _ {i} \ right \ Vert {\ big)}}}}$

dónde

${\ Displaystyle \ varepsilon \ {\ stackrel {\ mathrm {def}} {=}} \ f [x (t)] - \ varphi [x (t)] = x (t + 1) -c [x (t) ), t] - \ varphi [x (t)] = x (t + 1) -d (t + 1)}$.

Ver también

• Núcleo de función de base radial
• aprendizaje basado en instancias
• Tabulación adaptativa in situ
• Analítica predictiva
• Teoría del caos
• RBF jerárquico
• Controlador de articulación modelo cerebeloso
• Redes neuronales entrenadas instantáneamente

Referencias

Otras lecturas

• J. Moody y CJ Darken, "Aprendizaje rápido en redes de unidades de procesamiento sintonizadas localmente", Neural Computation, 1, 281-294 (1989). Consulte también Redes de función de base radial según Moody y Darken
• T. Poggio y F. Girosi, " Redes de aproximación y aprendizaje ", Proc. IEEE 78 (9), 1484-1487 (1990).
• Roger D. Jones , YC Lee, CW Barnes, GW Flake, K. Lee, PS Lewis y S. Qian ,? Aproximación de funciones y la predicción de series temporales con redes neuronales ,? Actas de la Conferencia conjunta internacional sobre redes neuronales, 17 al 21 de junio, pág. I-649 (1990).
• Martin D. Buhmann (2003). Funciones de base radial: teoría e implementaciones . Universidad de Cambridge. ISBN 0-521-63338-9.
• Yee, Paul V. y Haykin, Simon (2001). Redes de funciones de base radial regularizadas: teoría y aplicaciones . John Wiley. ISBN 0-471-35349-3.
• John R. Davies, Stephen V. Coggeshall, Roger D. Jones y Daniel Schutzer, "Intelligent Security Systems", en Freedman, Roy S., Flein, Robert A. y Lederman, Jess, Editors (1995). Inteligencia artificial en los mercados de capitales . Chicago: Irwin. ISBN 1-55738-811-3.CS1 maint: varios nombres: lista de autores ( enlace )
• Simon Haykin (1999). Redes neuronales: una base integral (2ª ed.). Upper Saddle River, Nueva Jersey: Prentice Hall. ISBN 0-13-908385-5.
• S. Chen, CFN Cowan y PM Grant, " Algoritmo de aprendizaje de mínimos cuadrados ortogonales para redes de función de base radial ", IEEE Transactions on Neural Networks, Vol 2, No 2 (Mar) 1991.