Problema de Monty Hall - Monty Hall problem
El problema de Monty Hall es un acertijo , en forma de acertijo de probabilidad , basado libremente en el programa de televisión estadounidense Let's Make a Deal y que lleva el nombre de su presentador original, Monty Hall . El problema fue planteado originalmente (y resuelto) en una carta de Steve Selvin al estadístico estadounidense en 1975. Se hizo famoso como una pregunta del lector Craig F. Whitaker citada en la columna "Ask Marilyn" de Marilyn vos Savant en la revista Parade. en 1990:
Suponga que está en un programa de juegos y tiene la opción de elegir entre tres puertas: detrás de una puerta hay un automóvil; detrás de los demás, cabras. Eliges una puerta, digamos el número 1, y el anfitrión, que sabe lo que hay detrás de las puertas, abre otra puerta, digamos el número 3, que tiene una cabra. Luego te dice: "¿Quieres elegir la puerta número 2?" ¿Le conviene cambiar de elección?
La respuesta de Vos Savant fue que el concursante debería cambiar a la otra puerta. Bajo los supuestos estándar, la estrategia de cambio tiene un2/3 probabilidad de ganar el coche, mientras que la estrategia que permanece con la elección inicial tiene sólo una1/3 probabilidad.
Cuando el jugador hace su elección por primera vez, hay un 2/3posibilidad de que el coche esté detrás de una de las puertas no elegidas. Esta probabilidad no cambia después de que el anfitrión abre una de las puertas no elegidas. Cuando el anfitrión proporciona información sobre las 2 puertas no elegidas (revelando que una de ellas no tiene el automóvil detrás), el2/3 La posibilidad de que el automóvil esté detrás de una de las puertas no elegidas se basa en la puerta no elegida y no revelada, a diferencia de la 1/3 posibilidad de que el coche esté detrás de la puerta que el concursante eligió inicialmente.
Las probabilidades dadas dependen de suposiciones específicas sobre cómo el anfitrión y el concursante eligen sus puertas. Una idea clave es que, bajo estas condiciones estándar, hay más información sobre las puertas 2 y 3 de la que estaba disponible al comienzo del juego cuando el jugador eligió la puerta 1: la acción deliberada del anfitrión agrega valor a la puerta que no eligió. elegir eliminar, pero no a la elegida originalmente por el concursante. Otra idea es que cambiar de puerta es una acción diferente a elegir entre las dos puertas restantes al azar, ya que la primera acción usa la información anterior y la última no. Otros posibles comportamientos del anfitrión distintos al descrito pueden revelar información adicional diferente, o ninguna en absoluto, y producir probabilidades diferentes.
Muchos lectores de la columna de vos Savant se negaron a creer que el cambio fuera beneficioso y rechazaron su explicación. Después de que apareció el problema en Parade , aproximadamente 10,000 lectores, incluidos casi 1,000 con doctorados , escribieron a la revista, la mayoría de ellos calificando incorrectamente a vos Savant. Incluso cuando se les dan explicaciones, simulaciones y pruebas matemáticas formales, mucha gente todavía no acepta que cambiar es la mejor estrategia. Paul Erdős , uno de los matemáticos más prolíficos de la historia, no quedó convencido hasta que se le mostró una simulación por computadora que demostraba el resultado predicho de vos Savant.
El problema es una paradoja de tipo verídico , porque la solución de Vos Savant es tan contradictoria que puede parecer absurda, pero no obstante es demostrablemente cierta. El problema de Monty Hall está estrechamente relacionado matemáticamente con el problema anterior de los Tres Prisioneros y con la paradoja de la caja de Bertrand, mucho más antigua .
Paradoja
Steve Selvin escribió una carta al estadístico estadounidense en 1975 describiendo un problema basado en el programa de juegos Let's Make a Deal , y lo denominó el "problema de Monty Hall" en una carta posterior. El problema es matemáticamente equivalente al problema de los Tres Prisioneros descrito en la columna "Juegos Matemáticos" de Martin Gardner en Scientific American en 1959 y al Problema de las Tres Conchas descrito en el libro de Gardner Aha Gotcha .
Supuestos estándar
Bajo los supuestos estándar, la probabilidad de ganar el auto después de cambiar es 2/3. La clave de esta solución es el comportamiento del anfitrión. Las ambigüedades en la versión Parade no definen explícitamente el protocolo del anfitrión. Sin embargo, la solución de Marilyn vos Savant impresa junto con la pregunta de Whitaker implica, y tanto Selven como vos Savant definen explícitamente, el papel del anfitrión de la siguiente manera:
- El anfitrión siempre debe abrir una puerta que no haya sido elegida por el concursante.
- El anfitrión siempre debe abrir una puerta para revelar una cabra y nunca el automóvil.
- El anfitrión siempre debe ofrecer la oportunidad de cambiar entre la puerta elegida originalmente y la puerta cerrada restante.
Cuando se modifica cualquiera de estos supuestos, puede cambiar la probabilidad de ganar cambiando de puerta como se detalla en la sección siguiente . Por lo general, también se presume que el automóvil está inicialmente oculto al azar detrás de las puertas y que, si el jugador inicialmente elige el automóvil, entonces la elección del anfitrión de qué puerta para esconder las cabras abrir es aleatoria. Algunos autores, de forma independiente o inclusiva, asumen que la elección inicial del jugador también es aleatoria.
Soluciones sencillas
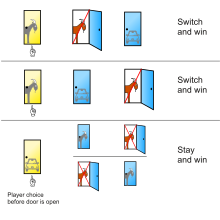
La solución presentada por vos Savant en Parade muestra las tres posibles disposiciones de un automóvil y dos cabras detrás de tres puertas y el resultado de quedarse o cambiar después de elegir inicialmente la puerta 1 en cada caso:
Detrás de la puerta 1 Detrás de la puerta 2 Detrás de la puerta 3 Resultado si se queda en la puerta # 1 Resultado si cambia a la puerta ofrecida Cabra Cabra Coche Gana cabra Gana coche Cabra Coche Cabra Gana cabra Gana coche Coche Cabra Cabra Gana coche Gana cabra
Un jugador que se queda con la opción inicial gana en solo una de cada tres de estas posibilidades igualmente probables, mientras que un jugador que cambia gana en dos de cada tres.
Una explicación intuitiva es que, si el competidor inicialmente recoge una cabra (2 de 3 puertas), el competidor se ganar el coche por el cambio porque la otra cabra ya no puede ser recogido, mientras que si el competidor inicialmente recoge el coche (1 de 3 puertas), el concursante no ganará el coche al cambiar. El hecho de que el anfitrión posteriormente revele una cabra en una de las puertas no elegidas no cambia nada sobre la probabilidad inicial.
La mayoría de la gente llega a la conclusión de que cambiar no importa porque hay dos puertas sin abrir y un automóvil y que es una elección 50/50. Esto sería cierto si el anfitrión abre una puerta al azar, pero ese no es el caso; la puerta abierta depende de la elección inicial del jugador, por lo que el supuesto de independencia no es válido. Antes de que el anfitrión abra una puerta, hay un1/3probabilidad de que el coche esté detrás de cada puerta. Si el automóvil está detrás de la puerta 1, el anfitrión puede abrir la puerta 2 o la puerta 3, por lo que la probabilidad de que el automóvil esté detrás de la puerta 1 y el anfitrión abra la puerta 3 es1/3 × 1/2 = 1/6. Si el coche está detrás de la puerta 2 (y el jugador ha elegido la puerta 1), el anfitrión debe abrir la puerta 3, por lo que la probabilidad de que el coche esté detrás de la puerta 2 y el anfitrión abra la puerta 3 es1/3 × 1 = 1/3. Estos son los únicos casos en los que el anfitrión abre la puerta 3, por lo que si el jugador ha elegido la puerta 1 y el anfitrión abre la puerta 3, es dos veces más probable que el coche esté detrás de la puerta 2 que la puerta 1. La clave es que si el coche está detrás de la puerta 2, el anfitrión debe abrir la puerta 3, pero si el automóvil está detrás de la puerta 1, el anfitrión puede abrir cualquier puerta.
Otra forma de entender la solución es considerar juntas las dos puertas originales no elegidas. Como dice Cecil Adams , "Monty está diciendo en efecto: puedes quedarte con una puerta o puedes tener las otras dos". los2/3La posibilidad de encontrar el automóvil no ha cambiado con la apertura de una de estas puertas porque Monty, conociendo la ubicación del automóvil, seguramente revelará una cabra. Entonces, la elección del jugador después de que el anfitrión abre una puerta no es diferente a si el anfitrión le ofreciera al jugador la opción de cambiar de la puerta elegida originalmente al conjunto de las dos puertas restantes. El interruptor en este caso claramente le da al jugador un2/3 probabilidad de elegir el coche.
Como dice Keith Devlin , "Al abrir su puerta, Monty le dice al concursante 'Hay dos puertas que no elegiste, y la probabilidad de que el premio esté detrás de una de ellas es2/3. Te ayudaré usando mi conocimiento de dónde está el premio para abrir una de esas dos puertas y mostrarte que no esconde el premio. Ahora puede aprovechar esta información adicional. Su elección de la puerta A tiene una probabilidad de 1 en 3 de ser la ganadora. No he cambiado eso. Pero al eliminar la puerta C, les he mostrado que la probabilidad de que la puerta B esconda el premio es 2 en 3. ' "
Vos Savant sugiere que la solución será más intuitiva con 1,000,000 de puertas en lugar de 3. En este caso, hay 999,999 puertas con cabras detrás y una puerta con premio. Después de que el jugador elige una puerta, el anfitrión abre 999.998 de las puertas restantes. En promedio, en 999,999 veces de 1,000,000, la puerta restante contendrá el premio. Intuitivamente, el jugador debería preguntarse qué tan probable es que, dado un millón de puertas, hayan logrado elegir la correcta inicialmente. Stibel et al propusieron que la demanda de memoria de trabajo se grava durante el problema de Monty Hall y que esto obliga a las personas a "colapsar" sus elecciones en dos opciones igualmente probables. Informan que cuando el número de opciones aumenta a más de 7 opciones (7 puertas), la gente tiende a cambiar con más frecuencia; sin embargo, la mayoría de los concursantes todavía juzgan incorrectamente la probabilidad de éxito en 50:50.
Vos Savant y el furor mediático
"¡Lo arruinaste, y lo arruinaste! Ya que parece que tienes dificultades para comprender el principio básico en funcionamiento aquí, te lo explicaré. Después de que el anfitrión revele una cabra, ahora tienes una posibilidad entre dos de estar en lo correcto . Cambie su selección o no, las probabilidades son las mismas. Hay suficiente analfabetismo matemático en este país, y no necesitamos que el coeficiente intelectual más alto del mundo se propague más. ¡Qué vergüenza! "
Scott Smith, Ph.D. Universidad de Florida
Vos Savant escribió en su primera columna sobre el problema de Monty Hall que el jugador debería cambiar. Recibió miles de cartas de sus lectores, la gran mayoría de las cuales, incluidas muchas de lectores con doctorados, no estaban de acuerdo con su respuesta. Durante 1990-1991, tres de sus columnas en Parade se dedicaron a la paradoja. Numerosos ejemplos de cartas de lectores de las columnas de Vos Savant se presentan y discuten en The Monty Hall Dilemma: A Cognitive Illusion Par Excellence .
La discusión se repitió en otros lugares (por ejemplo, en la columna del periódico " The Straight Dope " de Cecil Adams ) y se informó en los principales periódicos como The New York Times .
En un intento de aclarar su respuesta, propuso un juego de cáscaras para ilustrar: "Miras hacia otro lado y yo pongo un guisante debajo de una de las tres cáscaras. Luego te pido que pongas el dedo en una cáscara. Las probabilidades que tu elección contiene un guisante son 1/3, ¿acordado? Luego, simplemente levanto un caparazón vacío de los otros dos restantes. Como puedo (y haré) hacer esto independientemente de lo que hayas elegido, no hemos aprendido nada que nos permita revisar las probabilidades en el caparazón debajo de tu dedo ". También propuso una simulación similar con tres naipes.
Vos Savant comentó que, a pesar de cierta confusión fue causada por algunos lectores sin darse cuenta de que tenían que asumir que el anfitrión siempre debe revelar una cabra, casi todos sus numerosos corresponsales ha entendido bien los supuestos problemas, y todavía estaban inicialmente convencido de que vos de Savant respuesta ("interruptor") estaba mal.
Confusión y crítica
Fuentes de confusión
Cuando se les presentó por primera vez el problema de Monty Hall, una abrumadora mayoría de personas asume que cada puerta tiene la misma probabilidad y concluye que el cambio no importa. De 228 sujetos en un estudio, solo el 13% eligió cambiar. En su libro El poder del pensamiento lógico , el psicólogo cognitivo Massimo Piattelli Palmarini escribe: "Ningún otro acertijo estadístico se acerca tanto a engañar a todas las personas todo el tiempo [e] incluso los físicos Nobel dan sistemáticamente la respuesta incorrecta, y que ellos insisten en ello y están dispuestos a reprender por escrito a quienes proponen la respuesta correcta ". Las palomas expuestas repetidamente al problema muestran que aprenden rápidamente a cambiar siempre, a diferencia de los humanos.
La mayoría de las declaraciones del problema, en particular la de Parade , no coinciden con las reglas del programa de juegos real y no especifican completamente el comportamiento del anfitrión o que la ubicación del automóvil se selecciona al azar. Krauss y Wang conjeturan que las personas hacen las suposiciones estándar incluso si no se establecen explícitamente.
Aunque estos problemas son matemáticamente significativos, incluso cuando se controlan estos factores, casi todas las personas siguen pensando que cada una de las dos puertas sin abrir tiene la misma probabilidad y concluyen que el cambio no importa. Esta suposición de "probabilidad igual" es una intuición profundamente arraigada. La gente tiende fuertemente a pensar que la probabilidad se distribuye uniformemente entre tantas incógnitas como estén presentes, ya sea que lo esté o no.
El problema sigue atrayendo la atención de los psicólogos cognitivos. El comportamiento típico de la mayoría, es decir, no cambiar, puede explicarse por fenómenos conocidos en la literatura psicológica como:
- El efecto de dotación , en el que la gente tiende a sobrevalorar la probabilidad de ganar de la puerta ya elegida - ya "poseída".
- El sesgo del statu quo , en el que la gente prefiere quedarse con la elección de la puerta que ya ha hecho.
- Los errores de omisión frente a los errores de comisión tienen un efecto en el que, en igualdad de condiciones, la gente prefiere cometer errores por inacción (Quedarse) en lugar de actuar (Cambiar).
La evidencia experimental confirma que estas son explicaciones plausibles que no dependen de la intuición de la probabilidad. Otra posibilidad es que la intuición de las personas simplemente no se ocupa de la versión de libro de texto del problema, sino de la configuración de un programa de juegos real. Allí, existe la posibilidad de que el maestro del espectáculo juegue engañosamente abriendo otras puertas solo si inicialmente se eligió una puerta con el automóvil. Un maestro del espectáculo que juega engañosamente la mitad de las veces modifica las posibilidades de ganar en caso de que se le ofrezca cambiar a "igual probabilidad".
Crítica de las soluciones simples
Como ya se señaló, la mayoría de las fuentes en el campo de la probabilidad , incluidos muchos libros de texto de introducción a la probabilidad, resuelven el problema mostrando las probabilidades condicionales de que el automóvil está detrás de la puerta 1 y la puerta 2 son1/3 y 2/3 (no 1/2 y 1/2) dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3; En las subsecciones anteriores se dieron varias formas de obtener y comprender este resultado.
Entre estas fuentes hay varias que critican explícitamente las soluciones "simples" presentadas popularmente, diciendo que estas soluciones son "correctas pero ... inestables", o no "abordan el problema planteado", o son "incompletas", o son "poco convincentes y engañosas ", o son (más francamente)" falsas ".
Sasha Voloch (2015) escribió que "cualquier explicación que diga algo como 'la probabilidad de que la puerta 1 sea 1/3, y nada puede cambiar eso ... 'es automáticamente sospechoso: las probabilidades son expresiones de nuestra ignorancia sobre el mundo, y la nueva información puede cambiar el alcance de nuestra ignorancia ".
Algunos dicen que estas soluciones responden a una pregunta ligeramente diferente: una frase es "tienes que anunciar antes de que se abra una puerta si planeas cambiar".
Las soluciones simples muestran de varias maneras que un concursante que está decidido a cambiar ganará el auto con probabilidad 2/3y, por tanto, el cambio es la estrategia ganadora, si el jugador tiene que elegir de antemano entre "cambiar siempre" y "quedarse siempre". Sin embargo, la probabilidad de ganar cambiando siempre es un concepto lógicamente distinto de la probabilidad de ganar cambiando, dado que el jugador ha elegido la puerta 1 y el anfitrión ha abierto la puerta 3 . Como dice una fuente, "la distinción entre [estas preguntas] parece confundir a muchos". El hecho de que sean diferentes se puede demostrar variando el problema de modo que estas dos probabilidades tengan valores numéricos diferentes. Por ejemplo, suponga que el concursante sabe que Monty no elige la segunda puerta al azar entre todas las alternativas legales, sino que, cuando se le da la oportunidad de elegir entre dos puertas perdedoras, Monty abre la de la derecha. En esta situación, las siguientes dos preguntas tienen diferentes respuestas:
- ¿Cuál es la probabilidad de ganar el auto cambiando siempre ?
- ¿Cuál es la probabilidad de ganar el coche dado que el jugador ha elegido la puerta 1 y el anfitrión ha abierto la puerta 3 ?
La respuesta a la primera pregunta es 2/3, como se muestra correctamente en las soluciones "simples". Pero la respuesta a la segunda pregunta ahora es diferente: la probabilidad condicional de que el automóvil esté detrás de la puerta 1 o la puerta 2 dado que el anfitrión ha abierto la puerta 3 (la puerta de la derecha) es1/2. Esto se debe a que la preferencia de Monty por las puertas más a la derecha significa que abre la puerta 3 si el automóvil está detrás de la puerta 1 (que originalmente era con probabilidad1/3) o si el coche está detrás de la puerta 2 (también originalmente con probabilidad 1/3). Para esta variación, las dos preguntas producen respuestas diferentes. Sin embargo, siempre que la probabilidad inicial de que el automóvil esté detrás de cada puerta sea1/3, nunca es una desventaja para el concursante cambiar, ya que la probabilidad condicional de ganar al cambiar es siempre al menos 1/2.
En Morgan et al. , cuatro profesores universitarios publicaron un artículo en The American Statistician afirmando que vos Savant dio el consejo correcto pero el argumento equivocado. Creían que la pregunta pedía la posibilidad de que el coche estuviera detrás de la puerta 2 dada la elección inicial del jugador para la puerta 1 y la puerta abierta 3, y demostraron que esta posibilidad era algo intermedio.1/2y 1 dependiendo del proceso de decisión del anfitrión al que se le haya dado la opción. Solo cuando la decisión es completamente aleatoria es la oportunidad2/3.
En un comentario invitado y en cartas posteriores al editor, Morgan et al fueron apoyados por algunos escritores, criticados por otros; en cada caso, se publica una respuesta de Morgan et al junto con la carta o comentario en The American Statistician . En particular, vos Savant se defendió vigorosamente. Morgan et al se quejaron en su respuesta a vos Savant de que vos Savant todavía no había respondido realmente a su propio punto principal. Más tarde, en su respuesta a Hogbin y Nijdam, estuvieron de acuerdo en que era natural suponer que el anfitrión elige una puerta para abrirse completamente al azar, cuando tiene una opción, y por lo tanto, la probabilidad condicional de ganar al cambiar (es decir, condicional dada la situación en la que se encuentra el jugador cuando tiene que hacer su elección) tiene el mismo valor,2/3, como la probabilidad incondicional de ganar cambiando (es decir, promediada sobre todas las situaciones posibles). Esta igualdad ya fue enfatizada por Bell (1992), quien sugirió que la solución matemáticamente involucrada de Morgan et al atraería sólo a los estadísticos, mientras que la equivalencia de las soluciones condicionales e incondicionales en el caso de la simetría era intuitivamente obvia.
Existe un desacuerdo en la literatura acerca de si la formulación del problema de vos Savant, como se presenta en Parade , está formulando la primera o la segunda pregunta, y si esta diferencia es significativa. Behrends concluye que "hay que considerar el asunto con cuidado para ver que ambos análisis son correctos"; lo que no quiere decir que sean iguales. Varios críticos del artículo de Morgan et al. , cuyas contribuciones se publicaron junto con el artículo original, criticó a los autores por alterar la redacción de vos Savant y malinterpretar su intención. Un comentarista (William Bell) consideró una cuestión de gusto si se menciona explícitamente que (en las condiciones estándar), qué puerta abre el anfitrión es independiente de si se debe querer cambiar.
Entre las soluciones simples, la "solución de puertas combinadas" se acerca más a una solución condicional, como vimos en la discusión de enfoques que utilizan el concepto de probabilidades y el teorema de Bayes. Se basa en la intuición profundamente arraigada de que revelar información que ya se conoce no afecta las probabilidades . Pero, saber que el anfitrión puede abrir una de las dos puertas no elegidas para mostrar una cabra no significa que abrir una puerta específica no afectaría la probabilidad de que el automóvil esté detrás de la puerta elegida inicialmente. El caso es que, aunque sabemos de antemano que el anfitrión abrirá una puerta y revelará una cabra, no sabemos qué puerta abrirá. Si el anfitrión elige uniformemente al azar entre las puertas que esconden una cabra (como es el caso en la interpretación estándar), esta probabilidad de hecho permanece sin cambios, pero si el anfitrión puede elegir de manera no aleatoria entre tales puertas, entonces la puerta específica que abre el anfitrión revela información adicional. El anfitrión siempre puede abrir una puerta revelando una cabra y (en la interpretación estándar del problema) la probabilidad de que el automóvil esté detrás de la puerta elegida inicialmente no cambia, pero no es por lo primero que lo segundo sea cierto. Las soluciones basadas en la afirmación de que las acciones del anfitrión no pueden afectar la probabilidad de que el automóvil esté detrás del elegido inicialmente parecen persuasivas, pero la afirmación es simplemente falsa a menos que cada una de las dos opciones del anfitrión sean igualmente probables, si tiene una opción. Por tanto, la afirmación debe estar justificada; sin justificación, la solución es, en el mejor de los casos, incompleta. La respuesta puede ser correcta, pero el razonamiento utilizado para justificarla es defectuoso.
Soluciones que utilizan probabilidad condicional y otras soluciones.
Las soluciones simples anteriores muestran que un jugador con una estrategia de cambio gana el auto con probabilidad general 2/3, es decir, sin tener en cuenta qué puerta abrió el anfitrión. En contraste, la mayoría de las fuentes en el campo de la probabilidad calculan las probabilidades condicionales de que el automóvil esté detrás de la puerta 1 y la puerta 2 sean1/3 y 2/3 dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3. Las soluciones en esta sección consideran solo aquellos casos en los que el jugador eligió la puerta 1 y el anfitrión abrió la puerta 3.
Refinando la solución simple
Si asumimos que el anfitrión abre una puerta al azar, cuando se le da una opción, entonces la puerta que abre el anfitrión no nos da ninguna información sobre si el automóvil está detrás de la puerta 1. En las soluciones simples, ya hemos observado que la probabilidad de que el coche esté detrás de la puerta 1, la puerta elegida inicialmente por el jugador, es inicialmente 1/3. Además, el anfitrión ciertamente va a abrir una puerta (diferente), por lo que abrir una puerta ( cuya puerta no está especificada) no cambia esto.1/3debe ser la probabilidad media de que el coche esté detrás de la puerta 1 dado que el anfitrión eligió la puerta 2 y el anfitrión eligió la puerta 3 porque estas son las únicas dos posibilidades. Pero estas dos probabilidades son las mismas. Por lo tanto, ambos son iguales a1/3. Esto muestra que la probabilidad de que el automóvil esté detrás de la puerta 1, dado que el jugador inicialmente eligió esta puerta y dado que el anfitrión abrió la puerta 3, es1/3, y se deduce que la probabilidad de que el coche esté detrás de la puerta 2, dado que el jugador inicialmente eligió la puerta 1 y el anfitrión abrió la puerta 3, es 2/3. El análisis también muestra que la tasa de éxito general de2/3, que se logra cambiando siempre , no se puede mejorar, y subraya lo que ya puede haber sido intuitivamente obvio: la elección que enfrenta el jugador es que entre la puerta elegida inicialmente y la otra puerta que el anfitrión dejó cerrada, los números específicos en estas puertas son irrelevantes.
Probabilidad condicional por cálculo directo
Por definición, la probabilidad condicional de ganar al cambiar dado que el concursante inicialmente elige la puerta 1 y el anfitrión abre la puerta 3 es la probabilidad del evento "el coche está detrás de la puerta 2 y el anfitrión abre la puerta 3" dividida por la probabilidad de "el anfitrión abre la puerta 3 ". Estas probabilidades se pueden determinar con referencia a la tabla de probabilidad condicional a continuación, o a un árbol de decisión equivalente como se muestra a la derecha. La probabilidad condicional de ganar cambiando es1/3/1/3 + 1/6, cual es 2/3.
La siguiente tabla de probabilidad condicional muestra cómo 300 casos, en todos los cuales el jugador elige inicialmente la puerta 1, se dividirían, en promedio, de acuerdo con la ubicación del automóvil y la elección de la puerta para abrir por parte del anfitrión.
Teorema de Bayes
Muchos libros de texto y artículos sobre probabilidad en el campo de la teoría de la probabilidad derivan la solución de probabilidad condicional a través de una aplicación formal del teorema de Bayes ; entre ellos libros de Gill y Henze. El uso de la forma de probabilidades del teorema de Bayes, a menudo llamado regla de Bayes, hace que dicha derivación sea más transparente.
Inicialmente, es igualmente probable que el automóvil esté detrás de cualquiera de las tres puertas: las probabilidades en la puerta 1, puerta 2 y puerta 3 son 1: 1: 1 . Este sigue siendo el caso después de que el jugador ha elegido la puerta 1, por independencia. Según la regla de Bayes , las probabilidades posteriores en la ubicación del automóvil, dado que el anfitrión abre la puerta 3, son iguales a las probabilidades anteriores multiplicadas por el factor de Bayes o probabilidad, que es, por definición, la probabilidad de la nueva pieza. de información (el anfitrión abre la puerta 3) bajo cada una de las hipótesis consideradas (ubicación del coche). Ahora, dado que el jugador eligió inicialmente la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 es del 50% si el automóvil está detrás de la puerta 1, del 100% si el automóvil está detrás de la puerta 2, del 0% si el automóvil está detrás de la puerta 3. Por lo tanto el factor de Bayes consiste en las razones1/2 : 1: 0 o equivalentemente 1: 2: 0 , mientras que las probabilidades anteriores eran 1: 1: 1 . Por lo tanto, las probabilidades posteriores se vuelven iguales al factor de Bayes 1: 2: 0 . Dado que el anfitrión abrió la puerta 3, la probabilidad de que el automóvil esté detrás de la puerta 3 es cero, y es dos veces más probable que esté detrás de la puerta 2 que la puerta 1.
Richard Gill analiza la probabilidad de que el anfitrión abra la puerta 3 de la siguiente manera. Dado que el automóvil no está detrás de la puerta 1, es igualmente probable que esté detrás de la puerta 2 o 3. Por lo tanto, la probabilidad de que el anfitrión abra la puerta 3 es del 50%. Dado que el automóvil está detrás de la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 también es del 50%, porque, cuando el anfitrión tiene una opción, cualquier opción es igualmente probable. Por lo tanto, esté o no el automóvil detrás de la puerta 1, la probabilidad de que el anfitrión abra la puerta 3 es del 50%. La información "el anfitrión abre la puerta 3" aporta un factor de Bayes o una relación de probabilidad de 1: 1 , sobre si el automóvil está detrás de la puerta 1. Inicialmente, las probabilidades de que la puerta 1 oculte el automóvil eran 2: 1 . Por lo tanto, las probabilidades posteriores de que la puerta 1 oculte el automóvil siguen siendo las mismas que las probabilidades anteriores, 2: 1 .
En palabras, la información sobre qué puerta abre el anfitrión (¿puerta 2 o puerta 3?) No revela información alguna sobre si el automóvil está o no detrás de la puerta 1, y esto es precisamente lo que supuestamente es intuitivamente obvio por los partidarios de soluciones simples, o usando los modismos de las pruebas matemáticas, "obviamente cierto, por simetría".
Cálculo directo
Considere el evento Ci , que indica que el automóvil está detrás de la puerta número i , toma el valor Xi , para la elección del jugador, y el valor Hi , para el anfitrión que abre la puerta. El jugador elige inicialmente la puerta i = 1, C = X1 y el anfitrión abre la puerta i = 3, C = H3.
En este caso, tenemos:
P (H3 | X1) = 1/2 porque esta expresión solo depende de X1 , no de Ci . Entonces, en esta expresión en particular, la elección del anfitrión no depende de dónde esté el automóvil, y solo quedan dos puertas una vez que se elige X1 (por ejemplo, P (H1 | X1) = 0 ); y P (Ci, Xi) = P (Ci) P (Xi) porque Ci y Xi son eventos independientes (el jugador no sabe dónde está el automóvil para poder elegir).
Entonces, si el jugador selecciona inicialmente la puerta 1 y el anfitrión abre la puerta 3, demostramos que la probabilidad condicional de ganar al cambiar es:
De la regla de Bayes , sabemos que P (A, B) = P (A | B) P (B) = P (B | A) P (A) . Extendiendo esta lógica a múltiples eventos, por ejemplo A , B y C , obtenemos que podemos jugar con los diferentes subconjuntos de {A, B, C} para calcular la probabilidad de la intersección, como herramienta para simplificar el cálculo de nuestra la probabilidad condicional:
En nuestro caso, como sabemos que P (H3 | C2, X1) = 1 , estamos de suerte:
Solución de dominio estratégico
Volviendo a Nalebuff, el problema de Monty Hall también está muy estudiado en la literatura sobre teoría de juegos y teoría de decisiones , y también algunas soluciones populares corresponden a este punto de vista. Vos Savant pide una decisión, no una oportunidad. Y se desconocen los aspectos casuales de cómo se oculta el automóvil y cómo se abre una puerta no elegida. Desde este punto de vista, hay que recordar que el jugador tiene dos oportunidades para tomar decisiones: en primer lugar, qué puerta elegir inicialmente; y en segundo lugar, si cambiar o no. Dado que no sabe cómo está oculto el automóvil ni cómo el presentador toma decisiones, es posible que pueda aprovechar su primera oportunidad de elección, como para neutralizar las acciones del equipo que ejecuta el programa de preguntas, incluido el presentador.
Siguiendo a Gill, una estrategia de concursante implica dos acciones: la elección inicial de una puerta y la decisión de cambiar (o quedarse) que puede depender tanto de la puerta elegida inicialmente como de la puerta a la que el anfitrión ofrece cambiar. Por ejemplo, la estrategia de un concursante es "elegir la puerta 1, luego cambiar a la puerta 2 cuando se le ofrezca, y no cambiar a la puerta 3 cuando se le ofrezca". Existen doce de esas estrategias deterministas del concursante.
La comparación elemental de las estrategias de los concursantes muestra que, para cada estrategia A, existe otra estrategia B "elegir una puerta y luego cambiar pase lo que pase" que la domina. No importa cómo esté oculto el automóvil y no importa qué regla use el anfitrión cuando tiene que elegir entre dos cabras, si A gana el automóvil, B también lo hace. Por ejemplo, la estrategia A "elige la puerta 1 y luego quédate siempre con ella" está dominada por la estrategia B "elige la puerta 1 y luego siempre cambia después de que el anfitrión revela una puerta": A gana cuando la puerta 1 oculta el automóvil, mientras que B gana cuando una de las puertas 2 y 3 oculta el coche. De manera similar, la estrategia A "elegir la puerta 1 y luego cambiar a la puerta 2 (si se ofrece), pero no cambiar a la puerta 3 (si se ofrece)" está dominada por la estrategia B "elegir la puerta 3 y luego cambiar siempre".
La dominación es una razón de peso para buscar una solución entre las estrategias siempre cambiantes, bajo supuestos bastante generales sobre el entorno en el que el competidor está tomando decisiones. En particular, si el automóvil está oculto por medio de algún dispositivo de aleatorización, como lanzar un dado de tres lados simétrico o asimétrico, el dominio implica que una estrategia que maximice la probabilidad de ganar el automóvil estará entre las tres estrategias siempre cambiantes, a saber: ser la estrategia que inicialmente escoge la puerta menos probable y luego cambia sin importar qué puerta cambiar ofrezca el anfitrión.
El dominio estratégico vincula el problema de Monty Hall con la teoría de juegos . En la configuración del juego de suma cero de Gill, descartar las estrategias de no cambio reduce el juego a la siguiente variante simple: el anfitrión (o el equipo de TV) decide la puerta para esconder el automóvil, y el concursante elige dos puertas ( es decir, las dos puertas que quedan después de la primera elección nominal del jugador). La concursante gana (y su oponente pierde) si el automóvil está detrás de una de las dos puertas que eligió.
Soluciones por simulación
Una forma sencilla de demostrar que una estrategia de cambio realmente gana dos de cada tres veces con las suposiciones estándar es simular el juego con cartas . Se utilizan tres cartas de una baraja ordinaria para representar las tres puertas; una tarjeta 'especial' representa la puerta con el automóvil y otras dos tarjetas representan las puertas de las cabras.
La simulación se puede repetir varias veces para simular múltiples rondas del juego. El jugador elige una de las tres cartas, luego, mirando las dos cartas restantes, el 'anfitrión' descarta una carta de cabra. Si la carta que queda en la mano del anfitrión es la carta del coche, esto se registra como una ganancia por cambio; si el anfitrión tiene una tarjeta de cabra, la ronda se registra como una victoria permanente. Como este experimento se repite en varias rondas, es probable que la tasa de ganancia observada para cada estrategia se aproxime a su probabilidad de ganancia teórica, de acuerdo con la ley de los números grandes .
Las jugadas repetidas también aclaran por qué cambiar es la mejor estrategia. Después de que el jugador elige su carta, ya se determina si el cambio ganará la ronda para el jugador. Si esto no resulta convincente, la simulación se puede realizar con toda la plataforma. En esta variante, la tarjeta de automóvil va al host 51 de 52 veces y permanece con el host sin importar cuántas tarjetas que no sean de automóvil se descarten.
Variantes
Una variante común del problema, asumida por varios autores académicos como el problema canónico , no hace la suposición simplificadora de que el anfitrión debe elegir uniformemente la puerta para abrir, sino que usa alguna otra estrategia . La confusión en cuanto a qué formalización es autoritaria ha llevado a una considerable acritud, particularmente porque esta variante hace que las pruebas sean más complicadas sin alterar la optimización de la estrategia de cambio constante para el jugador. En esta variante, el jugador puede tener diferentes probabilidades de ganar dependiendo de la elección observada del anfitrión, pero en cualquier caso, la probabilidad de ganar al cambiar es al menos1/2(y puede ser tan alto como 1), mientras que la probabilidad general de ganar al cambiar sigue siendo exactamente2/3. A veces, las variantes se presentan sucesivamente en libros de texto y artículos destinados a enseñar los conceptos básicos de la teoría de la probabilidad y la teoría de juegos . También se han estudiado un número considerable de otras generalizaciones.
Otros comportamientos del anfitrión
La versión del problema de Monty Hall publicada en Parade en 1990 no establecía específicamente que el anfitrión siempre abriría otra puerta, o siempre ofrecería la opción de cambiar, o incluso nunca abriría la puerta revelando el automóvil. Sin embargo, vos Savant dejó en claro en su segunda columna de seguimiento que el comportamiento del anfitrión previsto solo podía ser lo que llevó al2/3probabilidad que dio como respuesta original. "Cualquier otra cosa es una cuestión diferente". "Prácticamente todos mis críticos entendieron el escenario pretendido. Yo personalmente leí casi tres mil cartas (de las muchas miles adicionales que llegaron) y encontré que casi todas insistían simplemente en que debido a que quedaban dos opciones (o un error equivalente), las posibilidades eran incluso. Muy pocos plantearon preguntas sobre la ambigüedad, y las cartas que realmente se publicaron en la columna no estaban entre esas pocas ". La respuesta sigue si el automóvil se coloca al azar detrás de cualquier puerta, el anfitrión debe abrir una puerta que muestre una cabra independientemente de la elección inicial del jugador y, si hay dos puertas disponibles, elige cuál abrir al azar. La siguiente tabla muestra una variedad de otros posibles comportamientos del anfitrión y el impacto en el éxito del cambio.
Determinar la mejor estrategia del jugador dentro de un conjunto dado de otras reglas que el anfitrión debe seguir es el tipo de problema que se estudia en la teoría de juegos . Por ejemplo, si no se requiere que el anfitrión haga la oferta para cambiar, el jugador puede sospechar que el anfitrión es malintencionado y hace las ofertas con más frecuencia si el jugador ha seleccionado inicialmente el automóvil. En general, la respuesta a este tipo de preguntas depende de las suposiciones específicas hechas sobre el comportamiento del anfitrión, y puede variar desde "ignorar al anfitrión por completo" hasta "lanzar una moneda y cambiar si sale cara"; consulte la última fila de la tabla a continuación.
Morgan et al y Gillman muestran una solución más general en la que el automóvil se coloca (uniformemente) al azar, pero el anfitrión no está obligado a elegir uniformemente al azar si el jugador ha seleccionado inicialmente el automóvil, que es la forma en que ambos interpretan el enunciado del problema. in Parade a pesar de las exenciones de responsabilidad del autor. Ambos cambiaron la redacción de la versión Parade para enfatizar ese punto cuando reafirmaron el problema. Consideran un escenario donde el anfitrión elige entre revelar dos cabras con una preferencia expresada como una probabilidad q , que tiene un valor entre 0 y 1. Si el anfitrión escoge al azar q sería1/2 y cambiar gana con probabilidad 2/3independientemente de la puerta que abra el anfitrión. Si el jugador elige la puerta 1 y la preferencia del anfitrión por la puerta 3 es q , entonces la probabilidad de que el anfitrión abra la puerta 3 y el automóvil esté detrás de la puerta 2 es1/3, mientras que la probabilidad de que el anfitrión abra la puerta 3 y el automóvil esté detrás de la puerta 1 es q/3. Estos son los únicos casos en los que el anfitrión abre la puerta 3, por lo que la probabilidad condicional de ganar al cambiar dado que el anfitrión abre la puerta 3 es1/3/1/3 + q / 3 que simplifica a 1/1 + q. Dado que q puede variar entre 0 y 1, esta probabilidad condicional puede variar entre1/2y 1. Esto significa que incluso sin obligar al anfitrión a elegir al azar si el jugador selecciona inicialmente el coche, el jugador nunca está peor si cambia. Sin embargo, ninguna de las fuentes sugiere que el jugador sepa cuál es el valor de q, por lo que el jugador no puede atribuir una probabilidad que no sea la2/3 que vos Savant asumió estaba implícito.
| Posibles comportamientos del anfitrión en un problema no especificado | |
|---|---|
| Comportamiento del anfitrión | Resultado |
| El anfitrión actúa como se indica en la versión específica del problema. | Cambiar gana el coche dos tercios de las veces. (Caso específico de la forma generalizada a continuación con p = q = 1/2) |
| El anfitrión siempre revela una cabra y siempre ofrece un cambio. Si tiene una opción, elige la cabra más a la izquierda con probabilidad p (que puede depender de la elección inicial del jugador) y la puerta más a la derecha con probabilidad q = 1 - p . | Si el anfitrión abre la puerta más a la derecha, el cambio gana con probabilidad 1 / (1+ q ). |
| "Monty from Hell": el anfitrión ofrece la opción de cambiar solo cuando la elección inicial del jugador es la puerta ganadora. | Cambiar siempre produce una cabra. |
| "Monty para leer la mente": el anfitrión ofrece la opción de cambiar en caso de que el invitado esté decidido a quedarse de todos modos o en caso de que el invitado cambie a una cabra. | Cambiar siempre produce una cabra. |
| "Angelic Monty": el anfitrión ofrece la opción de cambiar solo cuando el jugador ha elegido incorrectamente. | Cambiar siempre gana el coche. |
| "Monty Fall" o "Ignorant Monty": El anfitrión no sabe lo que hay detrás de las puertas, y abre una al azar que no deja al descubierto el coche. | Cambiar gana el coche la mitad del tiempo. |
| El anfitrión sabe lo que hay detrás de las puertas y (antes de la elección del jugador) elige al azar qué cabra revelar. Ofrece la opción de cambiar solo cuando la elección del jugador difiere de la suya. | Cambiar gana el coche la mitad del tiempo. |
| El anfitrión abre una puerta y hace la oferta de cambiar el 100% del tiempo si el concursante inicialmente eligió el auto, y el 50% del tiempo en caso contrario. | Cambio gana 1/2el tiempo en el equilibrio de Nash . |
| Teoría del juego de cuatro etapas para dos jugadores. El jugador juega contra los organizadores del programa (estación de TV) que incluye al anfitrión. Primera etapa: los organizadores eligen una puerta (la elección se mantiene en secreto para el jugador). Segunda etapa: el jugador hace una elección preliminar de puerta. Tercera etapa: el anfitrión abre una puerta. Cuarta etapa: el jugador toma una decisión final. El jugador quiere ganar el coche, la emisora de televisión quiere quedárselo. Este es un juego de dos personas de suma cero. Según el teorema de von Neumann de la teoría de juegos , si permitimos a ambas partes estrategias completamente aleatorias, existe una solución minimax o equilibrio de Nash . | Solución Minimax ( equilibrio de Nash ): el automóvil primero se oculta uniformemente al azar y el anfitrión luego elige la puerta uniforme aleatoria para abrir sin revelar el automóvil y diferente de la puerta del jugador; El jugador primero elige una puerta uniforme al azar y luego siempre cambia a otra puerta cerrada. Con su estrategia, el jugador tiene una probabilidad de ganar de al menos2/3, sin embargo, la estación de televisión juega; con la estrategia de la estación de televisión, la estación de televisión perderá con probabilidad a lo sumo2/3, como quiera que juegue el jugador. El hecho de que estas dos estrategias coincidan (al menos2/3, a lo sumo 2/3) demuestra que forman la solución minimax. |
| Como antes, pero ahora el anfitrión tiene la opción de no abrir ninguna puerta. | Solución Minimax ( equilibrio de Nash ): el automóvil primero se oculta uniformemente al azar y luego el anfitrión nunca abre una puerta; El jugador primero elige una puerta uniformemente al azar y luego nunca cambia. La estrategia del jugador garantiza una posibilidad de ganar de al menos1/3. La estrategia de la estación de televisión garantiza una pérdida de posibilidades de como máximo1/3. |
| Caso Deal or No Deal : el anfitrión le pide al jugador que abra una puerta, luego ofrece un interruptor en caso de que el auto no haya sido revelado. | Cambiar gana el coche la mitad del tiempo. |
N puertas
DL Ferguson (1975 en una carta a Selvin) sugiere una generalización de N- puertas del problema original en el que el anfitrión abre p puertas perdedoras y luego ofrece al jugador la oportunidad de cambiar; en esta variante, el cambio gana con probabilidad . Esta probabilidad es siempre mayor que , por lo que el cambio siempre trae una ventaja.
Incluso si el anfitrión abre solo una puerta ( ), es mejor que el jugador cambie en todos los casos. A medida que N crece, la ventaja disminuye y se acerca a cero. En el otro extremo, si el anfitrión abre todas las puertas perdedoras menos una ( p = N - 2), la ventaja aumenta a medida que N crece (la probabilidad de ganar al cambiar esN - 1/norte, que se acerca a 1 cuando N crece mucho).
Versión cuántica
Una versión cuántica de la paradoja ilustra algunos puntos sobre la relación entre la información clásica o no cuántica y la información cuántica , tal como se codifica en los estados de los sistemas mecánicos cuánticos. La formulación se basa libremente en la teoría cuántica de juegos . Las tres puertas son reemplazadas por un sistema cuántico que permite tres alternativas; abrir una puerta y mirar hacia atrás se traduce como hacer una medida particular. Las reglas se pueden establecer en este idioma y, una vez más, la elección del jugador es seguir con la elección inicial o cambiar a otra opción "ortogonal". La última estrategia resulta duplicar las posibilidades, al igual que en el caso clásico. Sin embargo, si el presentador del programa no ha aleatorizado la posición del premio de una manera totalmente mecánica cuántica, el jugador puede hacerlo aún mejor y, a veces, incluso puede ganar el premio con certeza.
Historia
El primero de varios acertijos de probabilidad relacionados con el problema de Monty Hall es la paradoja de la caja de Bertrand , planteada por Joseph Bertrand en 1889 en su Calcul des probabilités . En este rompecabezas, hay tres cajas: una caja que contiene dos monedas de oro, una caja con dos monedas de plata y una caja con una de cada una. Después de elegir una caja al azar y retirar una moneda al azar que resulta ser una moneda de oro, la pregunta es cuál es la probabilidad de que la otra moneda sea de oro. Como en el problema de Monty Hall, la respuesta intuitiva es1/2, pero la probabilidad es en realidad 2/3.
El problema de los Reclusos de tres , publicado en Martin Gardner 's juegos matemáticos columna en Scientific American en 1959 es equivalente al problema de Monty Hall. Este problema involucra a tres presos condenados, uno al azar de los cuales ha sido elegido en secreto para ser indultado. Uno de los prisioneros le ruega al alcaide que le diga el nombre de uno de los otros a ejecutar, argumentando que esto no revela información sobre su propio destino, pero aumenta sus posibilidades de ser indultado.1/3 para 1/2. El alcaide obliga, (en secreto) tirando una moneda al aire para decidir qué nombre proporcionar si el prisionero que pregunta es el que está siendo indultado. La pregunta es si conocer la respuesta del alcaide cambia las posibilidades del prisionero de ser indultado. Este problema es equivalente al problema de Monty Hall; el prisionero que hace la pregunta todavía tiene un1/3 posibilidad de ser perdonado, pero su colega anónimo tiene una 2/3 oportunidad.
Steve Selvin planteó el problema de Monty Hall en un par de cartas a The American Statistician en 1975. La primera carta presentaba el problema en una versión cercana a su presentación en Parade 15 años después. El segundo parece ser el primer uso del término "problema de Monty Hall". El problema es en realidad una extrapolación del programa de juegos. Monty Hall hizo abierta una puerta equivocada de crear entusiasmo, pero ofreció un premio menos conocido - por ejemplo, $ 100 en efectivo - en lugar de la opción de puertas de conmutación. Como le escribió Monty Hall a Selvin:
Y si alguna vez te subes a mi programa, las reglas se mantienen firmes para ti: no hay casillas de intercambio después de la selección.
- Monty Hall
Una versión del problema muy similar a la que apareció tres años después en Parade se publicó en 1987 en la sección Puzzles de The Journal of Economic Perspectives . Nalebuff, como escritores posteriores en economía matemática, ve el problema como un ejercicio simple y divertido de teoría de juegos .
"The Monty Hall Trap", el artículo de 1989 de Phillip Martin en Bridge Today , presentó el problema de Selvin como un ejemplo de lo que Martin llama la trampa de la probabilidad de tratar la información no aleatoria como si fuera aleatoria, y lo relaciona con conceptos en el juego de bridge. .
Una versión refundido del problema de Selvin aparecido en Marilyn vos Savant s' Pregunta Marilyn columna de preguntas y respuestas del desfile en septiembre de 1990. A pesar de vos Savant dio la respuesta correcta que el cambio iba a ganar dos tercios del tiempo, se estima la revista recibida 10,000 cartas, incluidas cerca de 1,000 firmadas por doctores, muchas en membretes de departamentos de matemáticas y ciencias, declarando que su solución era incorrecta. Debido a la abrumadora respuesta, Parade publicó cuatro columnas sin precedentes sobre el problema. Como resultado de la publicidad, el problema ganó el nombre alternativo de "Marilyn y las cabras".
En noviembre de 1990, tuvo lugar una discusión igualmente polémica del artículo de vos Savant en la columna de Cecil Adams " The Straight Dope ". Adams inicialmente respondió, incorrectamente, que las posibilidades de las dos puertas restantes deben ser de una en dos. Después de que un lector escribió para corregir las matemáticas del análisis de Adams, Adams estuvo de acuerdo en que matemáticamente se había equivocado. "Eliges la puerta n. ° 1. Ahora se te ofrece esta opción: abre la puerta n. ° 1 o abre la puerta n. ° 2 y la puerta n. ° 3. En este último caso, te quedas con el premio si está detrás de cualquiera de las puertas. dos de cada tres posibilidades de ganar el premio que uno de cada tres, ¿no? Si lo piensas bien, el problema original te ofrece básicamente la misma opción. Monty está diciendo en efecto: puedes quedarte con tu única puerta o puedes tener las otras dos puertas, una de las cuales (una puerta sin premio) te abriré ". Adams dijo que la versión Parade dejaba las limitaciones críticas sin declarar, y sin esas limitaciones, las posibilidades de ganar cambiando no eran necesariamente dos de cada tres (por ejemplo, no era razonable asumir que el anfitrión siempre abre una puerta). Numerosos lectores, sin embargo, escribieron para afirmar que Adams había tenido "razón la primera vez" y que las posibilidades correctas eran una entre dos.
La columna Parade y su respuesta recibieron una atención considerable en la prensa, incluida una historia de primera plana en el New York Times en la que se entrevistó al propio Monty Hall . Hall entendió el problema, le dio al reportero una demostración con las llaves del auto y le explicó cómo el juego real de Let's Make a Deal difería de las reglas del rompecabezas. En el artículo, Hall señaló que debido a que tenía control sobre la forma en que progresaba el juego, jugando con la psicología del concursante, la solución teórica no se aplicaba a la jugabilidad real del programa. Dijo que no le sorprendió la insistencia de los expertos en que la probabilidad era de 1 sobre 2. "Esa es la misma suposición que los concursantes harían en el programa después de que les mostré que no había nada detrás de una puerta", dijo. "Pensarían que las probabilidades en su puerta ahora habían subido a 1 en 2, por lo que odiaban ceder la puerta sin importar cuánto dinero les ofreciera. Al abrir esa puerta estábamos presionando. Lo llamamos Henry James tratamiento. Fue ' La vuelta del tornillo ' ". Hall aclaró que, como presentador de un programa de concursos, no tenía que seguir las reglas del rompecabezas en la columna de vos Savant y no siempre tenía que permitirle a una persona la oportunidad de cambiar (por ejemplo, podría abrir su puerta inmediatamente si era un puerta perdida, podría ofrecerles dinero para no pasar de una puerta perdedora a una puerta ganadora, o podría darles la oportunidad de cambiar solo si tuvieran una puerta ganadora). "Si se requiere que el anfitrión abra una puerta todo el tiempo y le ofrezca un interruptor, entonces usted debe tomar el interruptor", dijo. "Pero si tiene la opción de permitir un cambio o no, tenga cuidado. Caveat emptor. Todo depende de su estado de ánimo".
Ver también
- MythBusters Episodio 177 "Wheel of Mythfortune" - Elige una puerta
- Principio de elección restringida : aplicación similar de la actualización bayesiana en el puente de contrato
Acertijos similares en la teoría de la probabilidad y la decisión
Referencias
Bibliografía
- Adams, Cecil (2 de noviembre de 1990). "En Hagamos un trato , eliges la puerta n. ° 1. Monty abre la puerta n. ° 2, sin premio. ¿Te quedas con la puerta n. ° 1 o cambias a la n. ° 3?" . La droga recta . Consultado el 25 de julio de 2005 .
- Barbeau, Edward (1993). "Falacias, defectos y flimflam: el problema del coche y las cabras". The College Mathematics Journal . 24 (2): 149-154. doi : 10.1080 / 07468342.1993.11973519 .
- Behrends, Ehrhard (2008). Matemáticas de cinco minutos . Librería AMS. pag. 57. ISBN 978-0-8218-4348-2.
- Bell, William (agosto de 1992). "Comente sobre Vamos a hacer un trato por Morgan et al ". El estadístico estadounidense . 46 (3): 241.
- Carlton, Matthew (2005). "Pedigríes, premios y prisioneros: el mal uso de la probabilidad condicional" . Revista de Educación en Estadística . 13 (2). doi : 10.1080 / 10691898.2005.11910554 . S2CID 118792491 .
- Chun, Young H. (1991). "Problema del programa de juegos". OR / MS hoy . 18 (3): 9.
- D'Ariano, GM; Gill, RD; Keyl, M .; Kuemmerer, B .; Maassen, H .; Werner, RF (21 de febrero de 2002). "El problema de Quantum Monty Hall". Quant. Inf. Computación . 2 (5): 355–366. arXiv : quant-ph / 0202120 . Código bibliográfico : 2002quant.ph..2120D .
- Devlin, Keith (julio-agosto de 2003). "Ángulo de Devlin: Monty Hall" . La Asociación Matemática de América . Consultado el 23 de junio de 2014 .
- Devlin, Keith (diciembre de 2005). "Ángulo de Devlin: Monty Hall revisitado" . La Asociación Matemática de América . Consultado el 23 de junio de 2014 .
- Eisenhauer, Joseph G. (2001). "La matriz de Monty Hall" (PDF) . Enseñanza de la estadística . 22 (1): 17-20. doi : 10.1111 / 1467-9639.00005 . Archivado desde el original (PDF) el 1 de marzo de 2012 . Consultado el 9 de julio de 2012 .
- Enßlin, Torsten A .; Westerkamp, Margret (abril de 2018). "La racionalidad de la irracionalidad en el problema de Monty Hall". Annalen der Physik . 531 (3): 1800128. arXiv : 1804.04948 . Código bibliográfico : 2019AnP ... 53100128E . doi : 10.1002 / yp.201800128 . S2CID 56036255 .
- Falk, Ruma (1992). "Una mirada más cercana a las probabilidades de los famosos tres prisioneros". Cognición . 43 (3): 197–223. doi : 10.1016 / 0010-0277 (92) 90012-7 . PMID 1643813 . S2CID 39617738 .
- Flitney, Adrian P. y Abbott, Derek (2002). "Versión cuántica del problema de Monty Hall". Physical Review A . 65 (6): 062318. arXiv : quant-ph / 0109035 . Código Bibliográfico : 2002PhRvA..65f2318F . doi : 10.1103 / PhysRevA.65.062318 . S2CID 119417490 . Arte. No. 062318, 2002.
- Fox, Craig R. y Levav, Jonathan (2004). "Partition-Edit-Count: razonamiento extensional ingenuo en el juicio de probabilidad condicional" (PDF) . Revista de Psicología Experimental: General . 133 (4): 626–642. doi : 10.1037 / 0096-3445.133.4.626 . PMID 15584810 . Archivado desde el original (PDF) el 10 de abril de 2020.
- Gardner, Martin (octubre de 1959a). "Juegos matemáticos". Scientific American : 180–182. Reimpreso en The Second Scientific American Book of Mathematical Puzzles and DiversionsCS1 maint: posdata ( enlace )
- Gardner, Martin (noviembre de 1959b). "Juegos matemáticos". Scientific American : 188.
- Gardner, Martin (1982). ¡Ajá! Gotcha: Paradoxes to Puzzle and Delight . WH Freeman. ISBN 978-0716713616.
- Gill, Jeff (2002). Métodos bayesianos . Prensa CRC. págs. 8-10. ISBN 1-58488-288-3. ( copia en línea restringida , p. 8, en Google Books )CS1 maint: posdata ( enlace )
- Gill, Richard (2010). "Problema de Monty Hall". Enciclopedia internacional de ciencia estadística . Saltador. págs. 858–863. arXiv : 1002.3878v2 .
- Gill, Richard (febrero de 2011). "El problema de Monty Hall no es un rompecabezas de probabilidades (es un desafío en el modelado matemático)". Statistica Neerlandica . 65 (1): 58–71. arXiv : 1002.0651v3 . doi : 10.1111 / j.1467-9574.2010.00474.x .
- Gill, Richard (17 de marzo de 2011a). "El problema de Monty Hall" (PDF) . Instituto de Matemáticas, Universidad de Leiden, Holanda. págs. 10-13.
- Gillman, Leonard (1992). "El coche y las cabras". American Mathematical Monthly . 99 (1): 3–7. doi : 10.2307 / 2324540 . JSTOR 2324540 .
- Gilovich, T .; Medvec, VH y Chen, S. (1995). "Comisión, omisión y reducción de la disonancia: hacer frente al arrepentimiento en el problema" Monty Hall "". Revista de Personalidad y Psicología Social . 21 (2): 182-190. doi : 10.1177 / 0146167295212008 . S2CID 146500989 .
- Gnedin, Sasha (2011). "El juego de las branquias de Mondee" . El inteligente matemático . 34 : 34–41. doi : 10.1007 / s00283-011-9253-0 .
- Granberg, Donald (2014). El dilema de Monty Hall: una ilusión cognitiva por excelencia . Lumad / CreateSpace. ISBN 978-0996100809.
- Granberg, Donald (1996). "Cambiar o no cambiar". En vos Savant, Marilyn (ed.). El poder del pensamiento lógico . Prensa de San Martín. ISBN 0-312-30463-3. ( copia en línea restringida , p. 169, en Google Books )CS1 maint: posdata ( enlace )
- Granberg, Donald y Brown, Thad A. (1995). "El dilema de Monty Hall". Boletín de Personalidad y Psicología Social . 21 (7): 711–729. doi : 10.1177 / 0146167295217006 . S2CID 146329922 .
- Grinstead, Charles M. y Snell, J. Laurie (4 de julio de 2006). Introducción a la probabilidad de Grinstead y Snell (PDF) . Consultado el 2 de abril de 2008 .
- Hall, Monty (1975). "El problema de Monty Hall" . LetsMakeADeal.com . Consultado el 15 de enero de 2007 . Incluye carta del 12 de mayo de 1975 a Steve SelvinCS1 maint: posdata ( enlace )
- Henze, Norbert (2011) [1997]. Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls (9ª ed.). Saltador. págs. 50–51, 105–107. ISBN 978-3834818454. ( copia en línea restringida , p. 105, en Google Books )CS1 maint: posdata ( enlace )
- Herbranson, WT y Schroeder, J. (2010). "¿Son las aves más inteligentes que los matemáticos? Las palomas ( Columba livia ) funcionan de manera óptima en una versión del Dilema de Monty Hall" . Revista de Psicología Comparada . 124 (1): 1–13. doi : 10.1037 / a0017703 . PMC 3086893 . PMID 20175592 .
- Hogbin, M .; Nijdam, W. (2010). "Carta al editor en Hagamos un trato por Morgan et al ". El estadístico estadounidense . 64 (2): 193. doi : 10.1198 / tast.2010.09227 . S2CID 219595003 .
- Kahneman, D .; Knetsch, JL y Thaler, RH (1991). "Anomalías: el efecto de la dotación, la aversión a las pérdidas y el sesgo de status quo" . Revista de perspectivas económicas . 5 : 193-206. doi : 10.1257 / jep.5.1.193 .
- Kaivanto, K .; Kroll, EB y Zabinski, M. (2014). "Manipulación de desencadenadores de sesgo y comprensión de formularios de tareas en Monty Hall" (PDF) . Boletín de Economía . 34 (1): 89–98.
- Krauss, Stefan y Wang, XT (2003). "La psicología del problema de Monty Hall: descubrimiento de mecanismos psicológicos para resolver un acertijo tenaz" (PDF) . Revista de Psicología Experimental: General . 132 (1): 3-22. doi : 10.1037 / 0096-3445.132.1.3 . Consultado el 30 de marzo de 2008 .
- Lucas, Stephen; Rosenhouse, Jason y Schepler, Andrew (2009). "El problema de Monty Hall, reconsiderado" (PDF) . Revista de Matemáticas . 82 (5): 332–342. doi : 10.4169 / 002557009X478355 . Consultado el 9 de julio de 2012 .
- Martin, Phillip (1993) [1989]. Granovetter, Pamela; Granovetter, Matthew (eds.). La trampa de Monty Hall . Solo para expertos . Libros de Granovetter.
- Morgan, JP; Chaganty, NR; Dahiya, RC y Doviak, MJ (1991). "Hagamos un trato: el dilema del jugador". El estadístico estadounidense . 45 (4): 284-287. doi : 10.1080 / 00031305.1991.10475821 . JSTOR 2684453 .
- Morone, A. y Fiore, A. (2007). "Tres puertas de Monty Hall para tontos" . Dipartimento di Scienze Economiche e Metodi Matematici - Università di Bari, Sur de Europa Investigación en estudios económicos - SERIES Documento de trabajo núm. 0012.
- Mueser, Peter R. y Granberg, Donald (mayo de 1999). "El dilema de Monty Hall revisado: comprensión de la interacción de la definición del problema y la toma de decisiones" . Experimental . Biblioteca de la Universidad de Munich. Documento de trabajo 99–06 . Consultado el 10 de junio de 2010 .
- Nalebuff, Barry (otoño de 1987). "Rompecabezas: elija un telón, duelo, conversiones de dos puntos y más" . Revista de perspectivas económicas . 1 (2): 157-163. doi : 10.1257 / jep.1.2.157 .
- Rao, M. Bhaskara (agosto de 1992). "Comente sobre Vamos a hacer un trato por Morgan et al ". El estadístico estadounidense . 46 (3): 241–242.
- Rosenhouse, Jason (2009). El problema de Monty Hall . Prensa de la Universidad de Oxford. ISBN 978-0-19-536789-8.
- Rosenthal, Jeffrey S. (septiembre de 2005a). "Monty Hall, Monty Fall, Monty Crawl" (PDF) . Horizontes de matemáticas : 5–7.
- Rosenthal, Jeffrey S. (2005b). Golpeado por un rayo: el curioso mundo de las probabilidades . Harper Collins. ISBN 978-0-00-200791-7.
- Samuelson, W. y Zeckhauser, R. (1988). "Sesgo de status quo en la toma de decisiones". Revista de riesgo e incertidumbre . 1 : 7-59. CiteSeerX 10.1.1.632.3193 . doi : 10.1007 / bf00055564 . S2CID 5641133 .
- Selvin, Steve (febrero de 1975a). "Un problema de probabilidad (carta al editor)". El estadístico estadounidense . 29 (1): 67–71. doi : 10.1080 / 00031305.1975.10479121 . JSTOR 2683689 .
- Selvin, Steve (agosto de 1975b). "Sobre el problema de Monty Hall (carta al editor)". El estadístico estadounidense . 29 (3): 134. JSTOR 2683443 .
- Seymann, RG (1991). "Comente sobre Hagamos un trato : el dilema del jugador". El estadístico estadounidense . 45 (4): 287–288. doi : 10.2307 / 2684454 . JSTOR 2684454 .
- Stibel, Jeffrey ; Dror, Itiel; Ben-Zeev, Talia (2008). "La teoría de la elección que colapsa: disociar la elección y el juicio en la toma de decisiones" (PDF) . Teoría y Decisión .
- Tierney, John (21 de julio de 1991). "Detrás de las puertas de Monty Hall: ¿rompecabezas, debate y respuesta?" . The New York Times . Consultado el 18 de enero de 2008 .
- Vazsonyi, Andrew (diciembre de 1998 - enero de 1999). "¿Qué puerta tiene el Cadillac?" (PDF) . Línea de decisión : 17-19. Archivado desde el original (PDF) el 13 de abril de 2014 . Consultado el 16 de octubre de 2012 .Mantenimiento CS1: fecha y año ( enlace )
- VerBruggen, Robert (24 de febrero de 2015). "El problema de 'Monty Hall': todo el mundo está equivocado" . RealClearScience . Consultado el 12 de octubre de 2017 .
- Volokh, Sasha (2 de marzo de 2015). "Una respuesta 'fácil' al infame problema de Monty Hall" . The Washington Post . ISSN 0190-8286 . Consultado el 12 de octubre de 2017 .
- vos Savant, Marilyn (2012) [1990-1991]. "Problema del programa de juegos" . Desfile . Archivado desde el original el 29 de abril de 2012.
- vos Savant, Marilyn (9 de septiembre de 1990a). "Pregúntale a Marilyn" . Desfile : 16. Archivado desde el original el 21 de enero de 2013 . Consultado el 12 de noviembre de 2012 .
- vos Savant, Marilyn (2 de diciembre de 1990b). "Pregúntale a Marilyn" . Parade : 25. Archivado desde el original el 21 de enero de 2013 . Consultado el 12 de noviembre de 2012 .
- vos Savant, Marilyn (17 de febrero de 1991a). "Pregúntale a Marilyn" . Parade : 12. Archivado desde el original el 21 de enero de 2013 . Consultado el 12 de noviembre de 2012 .
- vos Savant, Marilyn (noviembre de 1991c). "Respuesta de Marilyn vos Savant". Cartas al editor. El estadístico estadounidense . 45 (4): 347.
- vos Savant, Marilyn (1996). El poder del pensamiento lógico . Prensa de San Martín. pag. 5 . ISBN 0-312-15627-8.
- Williams, Richard (2004). "Apéndice D: La controversia de Monty Hall" (PDF) . Notas del curso de Sociología Licenciado Estadística I . Consultado el 25 de abril de 2008 .
- Whitaker, Craig F. (9 de septiembre de 1990). "[Formulación de Marilyn vos Savant de la pregunta planteada en una carta de Craig Whitaker]. Pregúntale a Marilyn". Desfile : 16.
Otras lecturas
- Gill, Richard (2011b). "Problema de Monty Hall (versión 5)" . StatProb: la enciclopedia patrocinada por sociedades de estadística y probabilidad . Archivado desde el original el 21 de enero de 2016 . Consultado el 3 de abril de 2011 .
- vos Savant, Marilyn (7 de julio de 1991b). "Pregúntale a Marilyn" . Parade : 26. Archivado desde el original el 21 de enero de 2013 . Consultado el 12 de noviembre de 2012 .
- vos Savant, Marilyn (26 de noviembre de 2006). "Pregúntale a Marilyn". Desfile : 6.
enlaces externos
- El problema del programa de juegos : la pregunta y las respuestas originales en el sitio web de Marilyn vos Savant
- Universidad de California en San Diego, Monty Knows Version y Monty Does Not Know Version, Una explicación del juego
- Monty Hall en Curlie
- "Stick or switch? Probability and the Monty Hall problem" , BBC News Magazine , 11 de septiembre de 2013 (vídeo). El matemático Marcus du Sautoy explica la paradoja de Monty Hall.