Distribución logarítmica normal - Log-normal distribution

Logaritmo normal

Función de densidad de probabilidad 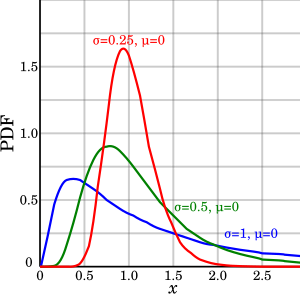Parámetro idéntico pero parámetros diferentes${\ Displaystyle \ mu}$${\ Displaystyle \ sigma}$
Función de distribución acumulativa ${\ Displaystyle \ mu = 0}$
Notación	${\ Displaystyle \ operatorname {Lognormal} (\ mu, \, \ sigma ^ {2})}$
Parámetros	${\ Displaystyle \ mu \ in (- \ infty, + \ infty)}$, ${\ Displaystyle \ sigma> 0}$
Apoyo	${\ Displaystyle x \ in (0, + \ infty)}$
PDF	${\ Displaystyle {\ frac {1} {x \ sigma {\ sqrt {2 \ pi}}}} \ \ exp \ left (- {\ frac {\ left (\ ln x- \ mu \ right) ^ {2 }} {2 \ sigma ^ {2}}} \ right)}$
CDF	${\ Displaystyle {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {\ ln x- \ mu} {\ sigma {\ sqrt {2}}}} \ bien bien]}$
Cuantil	${\ Displaystyle \ exp (\ mu + {\ sqrt {2 \ sigma ^ {2}}} \ operatorname {erf} ^ {- 1} (2p-1))}$
Significar	${\ Displaystyle \ exp \ left (\ mu + {\ frac {\ sigma ^ {2}} {2}} \ right)}$
Mediana	${\ Displaystyle \ exp (\ mu)}$
Modo	${\ Displaystyle \ exp (\ mu - \ sigma ^ {2})}$
Diferencia	${\ Displaystyle [\ exp (\ sigma ^ {2}) - 1] \ exp (2 \ mu + \ sigma ^ {2})}$
Oblicuidad	${\ Displaystyle (\ exp (\ sigma ^ {2}) + 2) {\ sqrt {\ exp (\ sigma ^ {2}) - 1}}}$
Ex. curtosis	${\ Displaystyle \ exp (4 \ sigma ^ {2}) + 2 \ exp (3 \ sigma ^ {2}) + 3 \ exp (2 \ sigma ^ {2}) - 6}$
Entropía	${\ Displaystyle \ log _ {2} (\ sigma e ^ {\ mu + {\ tfrac {1} {2}}} {\ sqrt {2 \ pi}})}$
MGF	definido solo para números con una parte real no positiva, ver texto
CF	la representación es asintóticamente divergente pero suficiente para propósitos numéricos${\ Displaystyle \ sum _ {n = 0} ^ {\ infty} {\ frac {(it) ^ {n}} {n!}} e ^ {n \ mu + n ^ {2} \ sigma ^ {2 } / 2}}$
Información de Fisher	${\ displaystyle {\ begin {pmatrix} 1 / \ sigma ^ {2} & 0 \\ 0 & 1/2 \ sigma ^ {2} \ end {pmatrix}}}$
Método de los momentos	${\ Displaystyle \ mu = \ log \ left ({\ frac {\ operatorname {E} [X] ^ {2}} {\ sqrt {\ operatorname {Var} [X] + \ operatorname {E} [X] ^ {2}}}} \ derecha)}$, ${\ Displaystyle \ sigma ^ {2} = \ log \ left ({\ frac {\ operatorname {Var} [X]} {\ operatorname {E} [X] ^ {2}}} + 1 \ right)}$

En la teoría de la probabilidad , una distribución logarítmica normal (o logarítmica normal) es una distribución de probabilidad continua de una variable aleatoria cuyo logaritmo se distribuye normalmente . Por tanto, si la variable aleatoria X tiene una distribución logarítmica normal, Y = ln ( X ) tiene una distribución normal. De manera equivalente, si Y tiene una distribución normal, entonces la función exponencial de Y , X = exp ( Y ) , tiene una distribución logarítmica normal. Una variable aleatoria que tiene una distribución logarítmica normal toma solo valores reales positivos. Es un modelo conveniente y útil para mediciones en ciencias exactas y de ingeniería , así como en medicina , economía y otros temas (por ejemplo, energías, concentraciones, longitudes, rendimientos financieros y otras métricas).

En ocasiones, la distribución se denomina distribución de Galton o distribución de Galton , en honor a Francis Galton . La distribución logarítmica normal también se ha asociado con otros nombres, como McAlister, Gibrat y Cobb – Douglas .

Un proceso logarítmico normal es la realización estadística del producto multiplicativo de muchas variables aleatorias independientes , cada una de las cuales es positiva. Esto se justifica considerando el teorema del límite central en el dominio logarítmico (a veces llamado ley de Gibrat ). La distribución logarítmica normal es la distribución de probabilidad de entropía máxima para una variable aleatoria X, para la cual se especifican la media y la varianza de ln ( X ) .

Definiciones

Generación y parámetros

Sea una variable normal estándar y sea y sea ​​dos números reales. Entonces, la distribución de la variable aleatoria ${\ Displaystyle Z}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma> 0}$

${\ Displaystyle X = e ^ {\ mu + \ sigma Z}}$

se llama distribución logarítmica normal con parámetros y . Estos son el valor esperado (o media ) y la desviación estándar del logaritmo natural de la variable , no la expectativa y la desviación estándar de sí misma. ${\ Displaystyle \ mu}$${\ Displaystyle \ sigma}$${\ Displaystyle X}$

Relación entre distribución normal y log-normal. Si se distribuye normalmente, entonces se distribuye logarítmicamente normalmente.${\ Displaystyle Y = \ mu + \ sigma Z}$${\ Displaystyle X \ sim e ^ {Y}}$

Esta relación es verdadera independientemente de la base de la función logarítmica o exponencial: si está distribuida normalmente, entonces también lo es para dos números positivos cualesquiera . Del mismo modo, si se distribuye normalmente en logaritmo, entonces también lo es , dónde . ${\ Displaystyle \ log _ {a} (X)}$${\ Displaystyle \ log _ {b} (X)}$${\ Displaystyle a, b \ neq 1}$${\ Displaystyle e ^ {Y}}$${\ Displaystyle a ^ {Y}}$${\ Displaystyle 0 <a \ neq 1}$

Para producir una distribución con la media y la varianza deseadas , se utilizan y${\ Displaystyle \ mu _ {X}}$${\ Displaystyle \ sigma _ {X} ^ {2}}$${\ Displaystyle \ mu = \ ln \ left ({\ frac {\ mu _ {X} ^ {2}} {\ sqrt {\ mu _ {X} ^ {2} + \ sigma _ {X} ^ {2 }}}}\Derecha)}$${\ Displaystyle \ sigma ^ {2} = \ ln \ left (1 + {\ frac {\ sigma _ {X} ^ {2}} {\ mu _ {X} ^ {2}}} \ right).}$

Alternativamente, se pueden utilizar los parámetros "multiplicativos" o "geométricos" y . Tienen una interpretación más directa: es la mediana de la distribución y es útil para determinar intervalos de "dispersión", ver más abajo. ${\ Displaystyle \ mu ^ {*} = e ^ {\ mu}}$${\ Displaystyle \ sigma ^ {*} = e ^ {\ sigma}}$${\ Displaystyle \ mu ^ {*}}$${\ Displaystyle \ sigma ^ {*}}$

Función de densidad de probabilidad

Una variable aleatoria positiva X tiene una distribución logarítmica normal (es decir, ), si el logaritmo natural de X se distribuye normalmente con media y varianza : ${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu _ {x}, \ sigma _ {x} ^ {2})}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma ^ {2}}$

${\ Displaystyle \ ln (X) \ sim {\ mathcal {N}} (\ mu, \ sigma ^ {2})}$

Sean y respectivamente la función de distribución de probabilidad acumulada y la función de densidad de probabilidad de la distribución N (0,1), entonces tenemos que ${\ Displaystyle \ Phi}$${\ Displaystyle \ varphi}$

${\ Displaystyle {\ begin {alineado} f_ {X} (x) & = {\ frac {\ rm {d}} {{\ rm {d}} x}} \ Pr (X \ leq x) = {\ frac {\ rm {d}} {{\ rm {d}} x}} \ Pr (\ ln X \ leq \ ln x) = {\ frac {\ rm {d}} {{\ rm {d}} x}} \ Phi \ left ({\ frac {\ ln x- \ mu} {\ sigma}} \ right) \\ [6pt] & = \ varphi \ left ({\ frac {\ ln x- \ mu} {\ sigma}} \ right) {\ frac {\ rm {d}} {{\ rm {d}} x}} \ left ({\ frac {\ ln x- \ mu} {\ sigma}} \ right ) = \ varphi \ left ({\ frac {\ ln x- \ mu} {\ sigma}} \ right) {\ frac {1} {\ sigma x}} \\ [6pt] & = {\ frac {1 } {x \ sigma {\ sqrt {2 \ pi \,}}}} \ exp \ left (- {\ frac {(\ ln x- \ mu) ^ {2}} {2 \ sigma ^ {2}} } \ right). \ end {alineado}}}$

Función de distribución acumulativa

La función de distribución acumulativa es

${\ Displaystyle F_ {X} (x) = \ Phi \ left ({\ frac {(\ ln x) - \ mu} {\ sigma}} \ right)}$

donde es la función de distribución acumulativa de la distribución normal estándar (es decir, N (0,1)). ${\ Displaystyle \ Phi}$

Esto también se puede expresar de la siguiente manera:

${\ Displaystyle {\ frac {1} {2}} \ left [1+ \ operatorname {erf} \ left ({\ frac {\ ln x- \ mu} {\ sigma {\ sqrt {2}}}} \ derecha) \ derecha] = {\ frac {1} {2}} \ operatorname {erfc} \ left (- {\ frac {\ ln x- \ mu} {\ sigma {\ sqrt {2}}}} \ right )}$

donde erfc es la función de error complementaria .

Logaritmo normal multivariante

Si es una distribución normal multivariante , entonces tiene una distribución logarítmica normal multivariante con media ${\ displaystyle {\ boldsymbol {X}} \ sim {\ mathcal {N}} ({\ boldsymbol {\ mu}}, \, {\ boldsymbol {\ Sigma}})}$${\ displaystyle {\ boldsymbol {Y}} = \ exp ({\ boldsymbol {X}})}$

${\ Displaystyle \ operatorname {E} [{\ boldsymbol {Y}}] _ {i} = e ^ {\ mu _ {i} + {\ frac {1} {2}} \ Sigma _ {ii}}, }$

y matriz de covarianza

${\ Displaystyle \ operatorname {Var} [{\ boldsymbol {Y}}] _ {ij} = e ^ {\ mu _ {i} + \ mu _ {j} + {\ frac {1} {2}} ( \ Sigma _ {ii} + \ Sigma _ {jj})} (e ^ {\ Sigma _ {ij}} - 1).}$

Dado que la distribución logarítmica normal multivariante no se usa ampliamente, el resto de esta entrada solo trata de la distribución univariante .

Función característica y función generadora de momentos

Todos los momentos de la distribución logarítmica normal existen y

${\ Displaystyle \ operatorname {E} [X ^ {n}] = e ^ {n \ mu + n ^ {2} \ sigma ^ {2} / 2}}$

Esto se puede derivar dejando dentro de la integral. Sin embargo, la distribución logarítmica normal no está determinada por sus momentos. Esto implica que no puede tener una función de generación de momento definida en una vecindad de cero. De hecho, el valor esperado no se define para ningún valor positivo del argumento , ya que la integral definitoria diverge. ${\ Displaystyle z = {\ tfrac {\ ln (x) - (\ mu + n \ sigma ^ {2})} {\ sigma}}}$${\ Displaystyle \ operatorname {E} [e ^ {tX}]}$${\ Displaystyle t}$

La función característica se define para valores reales de t , pero no se define para ningún valor complejo de t que tenga una parte imaginaria negativa y, por lo tanto, la función característica no es analítica en el origen. En consecuencia, la función característica de la distribución logarítmica normal no se puede representar como una serie convergente infinita. En particular, su serie formal de Taylor diverge: ${\ Displaystyle \ operatorname {E} [e ^ {itX}]}$

${\ Displaystyle \ sum _ {n = 0} ^ {\ infty} {\ frac {(it) ^ {n}} {n!}} e ^ {n \ mu + n ^ {2} \ sigma ^ {2 } / 2}}$

Sin embargo, se han obtenido varias representaciones de series divergentes alternativas .

No se conoce una fórmula de forma cerrada para la función característica con en el dominio de convergencia. Una fórmula aproximada relativamente simple está disponible en forma cerrada, y está dada por ${\ Displaystyle \ varphi (t)}$${\ Displaystyle t}$

${\ Displaystyle \ varphi (t) \ approx {\ frac {\ exp \ left (- {\ frac {W ^ {2} (- es \ sigma ^ {2} e ^ {\ mu}) + 2W (-it \ sigma ^ {2} e ^ {\ mu})} {2 \ sigma ^ {2}}} \ right)} {\ sqrt {1 + W (-it \ sigma ^ {2} e ^ {\ mu} )}}}}$

donde es la función W de Lambert . Esta aproximación se deriva mediante un método asintótico, pero se mantiene nítida en todo el dominio de convergencia de . ${\ Displaystyle W}$${\ Displaystyle \ varphi}$

Propiedades

una. es una variable logarítmica normal con . se calcula transformando a la variable normal , luego integrando su densidad sobre el dominio definido por (regiones azules), usando el método numérico de trazado de rayos. antes de Cristo. El pdf y el cdf de la función de la variable log-normal también se pueden calcular de esta manera.${\ Displaystyle y}$${\ Displaystyle \ mu = 1, \ sigma = 0.5}$${\ Displaystyle p (\ sin y> 0)}$${\ Displaystyle x = \ ln y}$${\ Displaystyle \ sin e ^ {x}> 0}$${\ Displaystyle \ sin y}$

Probabilidad en diferentes dominios

El contenido de probabilidad de una distribución logarítmica normal en cualquier dominio arbitrario se puede calcular con la precisión deseada transformando primero la variable a normal y luego integrándola numéricamente utilizando el método de trazado de rayos. ( Código de Matlab )

Probabilidades de funciones de una variable logarítmica normal

Dado que la probabilidad de un log-normal se puede calcular en cualquier dominio, esto significa que el CDF (y, en consecuencia, el pdf y el CDF inverso) de cualquier función de una variable logarítmica normal también se puede calcular. ( Código de Matlab )

Momentos geométricos o multiplicativos

La media geométrica o multiplicativa de la distribución log-normal es . Es igual a la mediana. La desviación estándar geométrica o multiplicativa es . ${\ Displaystyle \ operatorname {GM} [X] = e ^ {\ mu} = \ mu ^ {*}}$${\ Displaystyle \ operatorname {GSD} [X] = e ^ {\ sigma} = \ sigma ^ {*}}$

Por analogía con las estadísticas aritméticas, se puede definir una variación geométrica, y un coeficiente de variación geométrica de , , se ha propuesto. Se pretendía que este término fuera análogo al coeficiente de variación, para describir la variación multiplicativa en datos log-normales, pero esta definición de GCV no tiene una base teórica como una estimación de sí mismo (ver también Coeficiente de variación ). ${\ Displaystyle \ operatorname {GVar} [X] = e ^ {\ sigma ^ {2}}}$${\ Displaystyle \ operatorname {GCV} [X] = e ^ {\ sigma} -1}$${\ Displaystyle \ operatorname {CV}}$

Tenga en cuenta que la media geométrica es menor que la media aritmética. Esto se debe a la desigualdad AM-GM y es una consecuencia de que el logaritmo es una función cóncava . De hecho,

${\ Displaystyle \ operatorname {E} [X] = e ^ {\ mu + {\ frac {1} {2}} \ sigma ^ {2}} = e ^ {\ mu} \ cdot {\ sqrt {e ^ {\ sigma ^ {2}}}} = \ operatorname {GM} [X] \ cdot {\ sqrt {\ operatorname {GVar} [X]}}.}$

En finanzas, el término a veces se interpreta como una corrección de convexidad . Desde el punto de vista del cálculo estocástico , este es el mismo término de corrección que en el lema de Itō para el movimiento browniano geométrico . ${\ Displaystyle e ^ {- {\ frac {1} {2}} \ sigma ^ {2}}}$

Momentos aritméticos

Para cualquier número real o complejo n , el n -ésimo momento de una variable X con distribución logarítmica normal viene dado por

${\ Displaystyle \ operatorname {E} [X ^ {n}] = e ^ {n \ mu + {\ frac {1} {2}} n ^ {2} \ sigma ^ {2}}.}$

Específicamente, la media aritmética, el cuadrado esperado, la varianza aritmética y la desviación estándar aritmética de una variable X con distribución logarítmica normal vienen dadas respectivamente por:

${\ displaystyle {\ begin {alineado} \ operatorname {E} [X] & = e ^ {\ mu + {\ tfrac {1} {2}} \ sigma ^ {2}}, \\ [4pt] \ operatorname {E} [X ^ {2}] & = e ^ {2 \ mu +2 \ sigma ^ {2}}, \\ [4pt] \ operatorname {Var} [X] & = \ operatorname {E} [X ^ {2}] - \ operatorname {E} [X] ^ {2} = (\ operatorname {E} [X]) ^ {2} (e ^ {\ sigma ^ {2}} - 1) = e ^ {2 \ mu + \ sigma ^ {2}} (e ^ {\ sigma ^ {2}} - 1), \\ [4pt] \ operatorname {SD} [X] & = {\ sqrt {\ operatorname {Var } [X]}} = \ operatorname {E} [X] {\ sqrt {e ^ {\ sigma ^ {2}} - 1}} = e ^ {\ mu + {\ tfrac {1} {2}} \ sigma ^ {2}} {\ sqrt {e ^ {\ sigma ^ {2}} - 1}}, \ end {alineado}}}$

El coeficiente de variación aritmético es la razón . Para una distribución logarítmica normal es igual a ${\ Displaystyle \ operatorname {CV} [X]}$${\ displaystyle {\ tfrac {\ operatorname {SD} [X]} {\ operatorname {E} [X]}}}$

${\ Displaystyle \ operatorname {CV} [X] = {\ sqrt {e ^ {\ sigma ^ {2}} - 1}}.}$

Esta estimación a veces se denomina "CV geométrico" (GCV), debido a su uso de la varianza geométrica. Al contrario de la desviación estándar aritmética, el coeficiente de variación aritmético es independiente de la media aritmética.

Los parámetros μ y σ se pueden obtener si se conocen la media aritmética y la varianza aritmética:

${\ Displaystyle {\ begin {alineado} \ mu & = \ ln \ left ({\ frac {\ operatorname {E} [X] ^ {2}} {\ sqrt {\ operatorname {E} [X ^ {2} ]}}} \ right) = \ ln \ left ({\ frac {\ operatorname {E} [X] ^ {2}} {\ sqrt {\ operatorname {Var} [X] + \ operatorname {E} [X ] ^ {2}}}} \ right), \\ [4pt] \ sigma ^ {2} & = \ ln \ left ({\ frac {\ operatorname {E} [X ^ {2}]} {\ operatorname {E} [X] ^ {2}}} \ right) = \ ln \ left (1 + {\ frac {\ operatorname {Var} [X]} {\ operatorname {E} [X] ^ {2}} } \ right). \ end {alineado}}}$

Una distribución de probabilidad no está determinada únicamente por los momentos E [ X ⁿ ] = e ^{nμ + 1/2n 2 σ 2} para n ≥ 1. Es decir, existen otras distribuciones con el mismo conjunto de momentos. De hecho, existe toda una familia de distribuciones con los mismos momentos que la distribución logarítmica normal.

Moda, mediana, cuantiles

Comparación de la media , la mediana y la moda de dos distribuciones logarítmicas normales con diferente asimetría .

La moda es el punto de máximo global de la función de densidad de probabilidad. En particular, al resolver la ecuación , obtenemos que: ${\ Displaystyle (\ ln f) '= 0}$

${\ Displaystyle \ operatorname {Modo} [X] = e ^ {\ mu - \ sigma ^ {2}}.}$

Dado que la variable transformada logarítmicamente tiene una distribución normal y los cuantiles se conservan bajo transformaciones monótonas, los cuantiles de son ${\ Displaystyle Y = \ ln X}$${\ Displaystyle X}$

${\ Displaystyle q_ {X} (\ alpha) = e ^ {\ mu + \ sigma q _ {\ Phi} (\ alpha)} = \ mu ^ {*} (\ sigma ^ {*}) ^ {q _ {\ Phi} (\ alpha)},}$

donde es el cuantil de la distribución normal estándar. ${\ Displaystyle q _ {\ Phi} (\ alpha)}$

Específicamente, la mediana de una distribución logarítmica normal es igual a su media multiplicativa,

${\ Displaystyle \ operatorname {Med} [X] = e ^ {\ mu} = \ mu ^ {*}.}$

Expectativa parcial

La expectativa parcial de una variable aleatoria con respecto a un umbral se define como ${\ Displaystyle X}$${\ Displaystyle k}$

${\ Displaystyle g (k) = \ int _ {k} ^ {\ infty} xf_ {X} (x) \, dx.}$

Alternativamente, utilizando la definición de expectativa condicional , se puede escribir como . Para una variable aleatoria logarítmica normal, la expectativa parcial viene dada por: ${\ Displaystyle g (k) = \ operatorname {E} [X \ mid X> k] P (X> k)}$

${\ Displaystyle g (k) = \ int _ {k} ^ {\ infty} xf_ {X} (x) \, dx = e ^ {\ mu + {\ tfrac {1} {2}} \ sigma ^ { 2}} \, \ Phi \! \ Left ({\ frac {\ mu + \ sigma ^ {2} - \ ln k} {\ sigma}} \ right)}$

donde es la función de distribución acumulativa normal . La derivación de la fórmula se proporciona en la página Discusión . La fórmula de expectativa parcial tiene aplicaciones en seguros y economía , se utiliza para resolver la ecuación diferencial parcial que conduce a la fórmula de Black-Scholes . ${\ Displaystyle \ Phi}$

Expectativa condicional

La expectativa condicional de una variable aleatoria logarítmica normal, con respecto a un umbral, es su expectativa parcial dividida por la probabilidad acumulada de estar en ese rango: ${\ Displaystyle X}$${\ Displaystyle k}$

${\ Displaystyle {\ begin {alineado} E [X \ mid X <k] & = e ^ {\ mu + {\ frac {\ sigma ^ {2}} {2}}} \ cdot {\ frac {\ Phi \ left [{\ frac {\ ln (k) - \ mu - \ sigma ^ {2}} {\ sigma}} \ right]} {\ Phi \ left [{\ frac {\ ln (k) - \ mu } {\ sigma}} \ right]}} \\ [8pt] E [X \ mid X \ geqslant k] & = e ^ {\ mu + {\ frac {\ sigma ^ {2}} {2}}} \ cdot {\ frac {\ Phi \ left [{\ frac {\ mu + \ sigma ^ {2} - \ ln (k)} {\ sigma}} \ right]} {1- \ Phi \ left [{\ frac {\ ln (k) - \ mu} {\ sigma}} \ right]}} \\ [8pt] E [X \ mid X \ in [k_ {1}, k_ {2}]] & = e ^ {\ mu + {\ frac {\ sigma ^ {2}} {2}}} \ cdot {\ frac {\ Phi \ left [{\ frac {\ ln (k_ {2}) - \ mu - \ sigma ^ " {2}} {\ sigma}} \ right] - \ Phi \ left [{\ frac {\ ln (k_ {1}) - \ mu - \ sigma ^ {2}} {\ sigma}} \ right]} {\ Phi \ left [{\ frac {\ ln (k_ {2}) - \ mu} {\ sigma}} \ right] - \ Phi \ left [{\ frac {\ ln (k_ {1}) - \ mu} {\ sigma}} \ right]}} \ end {alineado}}}$

Parametrizaciones alternativas

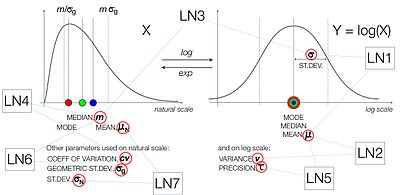
Además de la caracterización mediante o , aquí hay varias formas de parametrizar la distribución logarítmica normal. ProbOnto , la base de conocimientos y la ontología de distribuciones de probabilidad enumera siete de tales formas:${\ Displaystyle \ mu, \ sigma}$${\ Displaystyle \ mu ^ {*}, \ sigma ^ {*}}$

Resumen de parametrizaciones de las distribuciones log-normales.

• LogNormal1 (μ, σ) con media , μ y desviación estándar , σ, ambas en la escala logarítmica

  ${\ Displaystyle P (x; {\ boldsymbol {\ mu}}, {\ boldsymbol {\ sigma}}) = {\ frac {1} {x \ sigma {\ sqrt {2 \ pi}}}} \ exp \ izquierda [- {\ frac {(\ ln x- \ mu) ^ {2}} {2 \ sigma ^ {2}}} \ right]}$

• LogNormal2 (μ, υ) con media, μ y varianza, υ, ambos en la escala logarítmica

  ${\ displaystyle P (x; {\ boldsymbol {\ mu}}, {\ boldsymbol {v}}) = {\ frac {1} {x {\ sqrt {v}} {\ sqrt {2 \ pi}}} } \ exp \ left [- {\ frac {(\ ln x- \ mu) ^ {2}} {2v}} \ right]}$

• LogNormal3 (m, σ) con mediana , m, en la escala natural y desviación estándar, σ, en la escala logarítmica

  ${\ displaystyle P (x; {\ boldsymbol {m}}, {\ boldsymbol {\ sigma}}) = {\ frac {1} {x \ sigma {\ sqrt {2 \ pi}}}} \ exp \ left [- {\ frac {\ ln ^ {2} (x / m)} {2 \ sigma ^ {2}}} \ right]}$

• LogNormal4 (m, cv) con mediana, m y coeficiente de variación , cv, ambos en la escala natural

  ${\ displaystyle P (x; {\ boldsymbol {m}}, {\ boldsymbol {cv}}) = {\ frac {1} {x {\ sqrt {\ ln (cv ^ {2} +1)}} { \ sqrt {2 \ pi}}}} \ exp \ left [- {\ frac {\ ln ^ {2} (x / m)} {2 \ ln (cv ^ {2} +1)}} \ right] }$

• LogNormal5 (μ, τ) con media, μ y precisión, τ, ambos en la escala logarítmica

  ${\ displaystyle P (x; {\ boldsymbol {\ mu}}, {\ boldsymbol {\ tau}}) = {\ sqrt {\ frac {\ tau} {2 \ pi}}} {\ frac {1} { x}} \ exp \ left [- {\ frac {\ tau} {2}} (\ ln x- \ mu) ^ {2} \ right]}$

• LogNormal6 (m, σ _g ) con mediana, m, y desviación estándar geométrica , σ _g , ambos en la escala natural

  ${\ Displaystyle P (x; {\ boldsymbol {m}}, {\ boldsymbol {\ sigma _ {g}}}) = {\ frac {1} {x \ ln (\ sigma _ {g}) {\ sqrt {2 \ pi}}}} \ exp \ left [- {\ frac {\ ln ^ {2} (x / m)} {2 \ ln ^ {2} (\ sigma _ {g})}} \ right ]}$

• LogNormal7 (μ _N , σ _N ) con media, μ _N y desviación estándar, σ _N , ambas en la escala natural

  ${\ Displaystyle P (x; {\ boldsymbol {\ mu _ {N}}}, {\ boldsymbol {\ sigma _ {N}}}) = {\ frac {1} {x {\ sqrt {2 \ pi \ ln \ left (1+ \ sigma _ {N} ^ {2} / \ mu _ {N} ^ {2} \ right)}}}} \ exp \ left (- {\ frac {{\ Big [} \ ln x- \ ln {\ frac {\ mu _ {N}} {\ sqrt {1+ \ sigma _ {N} ^ {2} / \ mu _ {N} ^ {2}}}} {\ Big] } ^ {2}} {2 \ ln (1+ \ sigma _ {N} ^ {2} / \ mu _ {N} ^ {2})}} \ right)}$

Ejemplos de re-parametrización

Considere la situación en la que a uno le gustaría ejecutar un modelo utilizando dos herramientas de diseño óptimas diferentes, por ejemplo, PFIM y PopED. El primero admite la parametrización LN2, el último LN7, respectivamente. Por lo tanto, se requiere la re-parametrización, de lo contrario las dos herramientas producirían resultados diferentes.

Para la transición, se mantienen las siguientes fórmulas . ${\ Displaystyle \ operatorname {LN2} (\ mu, v) \ a \ operatorname {LN7} (\ mu _ {N}, \ sigma _ {N})}$${\ Displaystyle \ mu _ {N} = \ exp (\ mu + v / 2) {\ text {y}} \ sigma _ {N} = \ exp (\ mu + v / 2) {\ sqrt {\ exp (v) -1}}}$

Para la transición, se mantienen las siguientes fórmulas . ${\ Displaystyle \ operatorname {LN7} (\ mu _ {N}, \ sigma _ {N}) \ to \ operatorname {LN2} (\ mu, v)}$${\ Displaystyle \ mu = \ ln {\ Big (} \ mu _ {N} / {\ sqrt {1+ \ sigma _ {N} ^ {2} / \ mu _ {N} ^ {2}}} { \ Big)} {\ text {y}} v = \ ln (1+ \ sigma _ {N} ^ {2} / \ mu _ {N} ^ {2})}$

Todas las fórmulas de re-parametrización restantes se pueden encontrar en el documento de especificaciones en el sitio web del proyecto.

Poder múltiple, recíproco

• Multiplicación por una constante: si entonces${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle aX \ sim \ operatorname {Lognormal} (\ mu + \ ln a, \ \ sigma ^ {2}).}$
• Recíproco: si entonces${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle {\ tfrac {1} {X}} \ sim \ operatorname {Lognormal} (- \ mu, \ \ sigma ^ {2}).}$
• Poder: Si entonces para${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle X ^ {a} \ sim \ operatorname {Lognormal} (a \ mu, \ a ^ {2} \ sigma ^ {2})}$${\ Displaystyle a \ neq 0.}$

Multiplicación y división de variables aleatorias independientes logarítmicas normales

Si se multiplican [se dividen] dos variables independientes , logarítmicas normales y , el producto [razón] vuelve a ser logarítmico normal, con los parámetros [ ] y , donde . Esto se generaliza fácilmente al producto de tales variables. ${\ Displaystyle X_ {1}}$${\ Displaystyle X_ {2}}$${\ Displaystyle \ mu = \ mu _ {1} + \ mu _ {2}}$${\ Displaystyle \ mu = \ mu _ {1} - \ mu _ {2}}$${\ Displaystyle \ sigma}$${\ Displaystyle \ sigma ^ {2} = \ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2}}$${\ Displaystyle n}$

De manera más general, si son variables independientes, con distribución logarítmica normal, entonces${\ Displaystyle X_ {j} \ sim \ operatorname {Lognormal} (\ mu _ {j}, \ sigma _ {j} ^ {2})}$${\ Displaystyle n}$${\ Displaystyle Y = \ textstyle \ prod _ {j = 1} ^ {n} X_ {j} \ sim \ operatorname {Lognormal} {\ Big (} \ textstyle \ sum _ {j = 1} ^ {n} \ mu _ {j}, \ \ sum _ {j = 1} ^ {n} \ sigma _ {j} ^ {2} {\ Big)}.}$

Teorema del límite central multiplicativo

La media geométrica o multiplicativa de variables aleatorias positivas independientes distribuidas de manera idéntica muestra, para aproximadamente una distribución logarítmica normal con parámetros y , asumiendo que es finito. ${\ Displaystyle n}$${\ Displaystyle X_ {i}}$${\ Displaystyle n \ to \ infty}$${\ Displaystyle \ mu = E [\ ln (X_ {i})]}$${\ Displaystyle \ sigma ^ {2} = {\ mbox {var}} [\ ln (X_ {i})] / n}$${\ Displaystyle \ sigma ^ {2}}$

De hecho, las variables aleatorias no tienen que estar distribuidas de forma idéntica. Es suficiente que todas las distribuciones de tengan varianza finita y satisfagan las demás condiciones de cualquiera de las muchas variantes del teorema del límite central . ${\ Displaystyle \ ln (X_ {i})}$

Esto se conoce comúnmente como ley de Gibrat .

Otro

Un conjunto de datos que surge de la distribución log-normal tiene una curva de Lorenz simétrica (ver también el coeficiente de asimetría de Lorenz ).

Las medias armónicas , geométricas y aritméticas de esta distribución están relacionadas; tal relación viene dada por ${\ Displaystyle H}$${\ Displaystyle G}$${\ Displaystyle A}$

${\ Displaystyle H = {\ frac {G ^ {2}} {A}}.}$

Las distribuciones logarítmicas normales son infinitamente divisibles , pero no son distribuciones estables de las que se puedan extraer fácilmente.

Distribuciones relacionadas

• Si es una distribución normal , entonces${\ Displaystyle X \ sim {\ mathcal {N}} (\ mu, \ sigma ^ {2})}$${\ Displaystyle \ exp (X) \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2}).}$
• Si se distribuye logarítmicamente normalmente, entonces es una variable aleatoria normal.${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle \ ln (X) \ sim {\ mathcal {N}} (\ mu, \ sigma ^ {2})}$
• Sean variables independientes logarítmicamente distribuidas normalmente con parámetros y posiblemente variables , y . La distribución de no tiene una expresión de forma cerrada, pero puede aproximarse razonablemente mediante otra distribución logarítmica normal en la cola derecha. Se ha caracterizado su función de densidad de probabilidad en la vecindad de 0 y no se parece a ninguna distribución logarítmica normal. Una aproximación comúnmente utilizada debida a LF Fenton (pero previamente establecida por RI Wilkinson y justificada matemáticamente por Marlow) se obtiene al hacer coincidir la media y la varianza de otra distribución logarítmica normal:${\ Displaystyle X_ {j} \ sim \ operatorname {Lognormal} (\ mu _ {j}, \ sigma _ {j} ^ {2}) \}$${\ Displaystyle \ sigma}$${\ Displaystyle \ mu}$${\ Displaystyle Y = \ textstyle \ sum _ {j = 1} ^ {n} X_ {j}}$${\ Displaystyle Y}$${\ Displaystyle Z}$

${\ Displaystyle {\ begin {alineado} \ sigma _ {Z} ^ {2} & = \ ln \! \ left [{\ frac {\ sum e ^ {2 \ mu _ {j} + \ sigma _ {j } ^ {2}} (e ^ {\ sigma _ {j} ^ {2}} - 1)} {(\ sum e ^ {\ mu _ {j} + \ sigma _ {j} ^ {2} / 2}) ^ {2}}} + 1 \ right], \\\ mu _ {Z} & = \ ln \! \ Left [\ sum e ^ {\ mu _ {j} + \ sigma _ {j} ^ {2} / 2} \ right] - {\ frac {\ sigma _ {Z} ^ {2}} {2}}. \ End {alineado}}}$

En el caso de que todos tengan el mismo parámetro de varianza , estas fórmulas se simplifican a ${\ Displaystyle X_ {j}}$${\ Displaystyle \ sigma _ {j} = \ sigma}$

${\ Displaystyle {\ begin {alineado} \ sigma _ {Z} ^ {2} & = \ ln \! \ left [(e ^ {\ sigma ^ {2}} - 1) {\ frac {\ sum e ^ {2 \ mu _ {j}}} {(\ sum e ^ {\ mu _ {j}}) ^ {2}}} + 1 \ right], \\\ mu _ {Z} & = \ ln \ ! \ left [\ sum e ^ {\ mu _ {j}} \ right] + {\ frac {\ sigma ^ {2}} {2}} - {\ frac {\ sigma _ {Z} ^ {2} } {2}}. \ End {alineado}}}$

Para una aproximación más precisa, se puede utilizar el método de Monte Carlo para estimar la función de distribución acumulativa, el pdf y la cola derecha.

La suma de las variables aleatorias correlacionadas con distribución logarítmica normal también se puede aproximar mediante una distribución logarítmica normal

${\ Displaystyle {\ begin {alineado} S _ {+} & = \ operatorname {E} \ left [\ sum _ {i} X_ {i} \ right] = \ sum _ {i} \ operatorname {E} [X_ {i}] = \ sum _ {i} e ^ {\ mu _ {i} + \ sigma _ {i} ^ {2} / 2} \\\ sigma _ {Z} ^ {2} & = 1 / S _ {+} ^ {2} \, \ sum _ {i, j} \ operatorname {cor} _ {ij} \ sigma _ {i} \ sigma _ {j} \ operatorname {E} [X_ {i}] \ operatorname {E} [X_ {j}] = 1 / S _ {+} ^ {2} \, \ sum _ {i, j} \ operatorname {cor} _ {ij} \ sigma _ {i} \ sigma _ {j} e ^ {\ mu _ {i} + \ sigma _ {i} ^ {2} / 2} e ^ {\ mu _ {j} + \ sigma _ {j} ^ {2} / 2} \ \\ mu _ {Z} & = \ ln \ left (S _ {+} \ right) - \ sigma _ {Z} ^ {2} / 2 \ end {alineado}}}$

• Si entonces se dice que tiene una distribución logarítmica normal de tres parámetros con soporte . , .${\ Displaystyle X \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle X + c}$${\ Displaystyle x \ in (c, + \ infty)}$${\ Displaystyle \ operatorname {E} [X + c] = \ operatorname {E} [X] + c}$${\ Displaystyle \ operatorname {Var} [X + c] = \ operatorname {Var} [X]}$
• La distribución logarítmica normal es un caso especial de la distribución SU de Johnson semilimitada .
• Si es con , entonces ( distribución Suzuki ).${\ Displaystyle X \ mid Y \ sim \ operatorname {Rayleigh} (Y) \,}$${\ Displaystyle Y \ sim \ operatorname {Lognormal} (\ mu, \ sigma ^ {2})}$${\ Displaystyle X \ sim \ operatorname {Suzuki} (\ mu, \ sigma)}$
• Se puede obtener un sustituto del log-normal cuya integral se puede expresar en términos de funciones más elementales con base en la distribución logística para obtener una aproximación de la CDF

${\ Displaystyle F (x; \ mu, \ sigma) = \ left [\ left ({\ frac {e ^ {\ mu}} {x}} \ right) ^ {\ pi / (\ sigma {\ sqrt { 3}})} + 1 \ right] ^ {- 1}.}$

Esta es una distribución log-logística .

Inferencia estadística

Estimación de parámetros

Para determinar los estimadores de máxima verosimilitud de los parámetros de distribución logarítmica normal μ y σ , podemos utilizar el mismo procedimiento que para la distribución normal . Tenga en cuenta que

${\ Displaystyle L (\ mu, \ sigma) = \ prod _ {i = 1} ^ {n} {\ frac {1} {x_ {i}}} \ varphi _ {\ mu, \ sigma} (\ ln x_ {i})}$,

donde es la función de densidad de la distribución normal . Por lo tanto, la función logarítmica de verosimilitud es ${\ Displaystyle \ varphi _ {}}$${\ Displaystyle {\ mathcal {N}} (\ mu, \ sigma ^ {2})}$

${\ Displaystyle \ ell (\ mu, \ sigma \ mid x_ {1}, x_ {2}, \ ldots, x_ {n}) = - \ sum _ {i} \ ln x_ {i} + \ ell _ { N} (\ mu, \ sigma \ mid \ ln x_ {1}, \ ln x_ {2}, \ dots, \ ln x_ {n})}$.

Dado que el primer término es constante con respecto a μ y σ , ambas funciones de verosimilitud logarítmica, y , alcanzan su máximo con el mismo y . Por tanto, los estimadores de máxima verosimilitud son idénticos a los de una distribución normal para las observaciones , ${\ Displaystyle \ ell}$${\ Displaystyle \ ell _ {N}}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma}$${\ Displaystyle \ ln x_ {1}, \ ln x_ {2}, \ dots, \ ln x_ {n})}$

${\ Displaystyle {\ widehat {\ mu}} = {\ frac {\ sum _ {k} \ ln x_ {k}} {n}}, \ qquad {\ widehat {\ sigma}} ^ {2} = { \ frac {\ sum _ {k} \ left (\ ln x_ {k} - {\ widehat {\ mu}} \ right) ^ {2}} {n}}.}$

Para n finito , estos estimadores están sesgados. Mientras que el sesgo para es insignificante, se obtiene un estimador menos sesgado para la distribución normal reemplazando el denominador n por n-1 en la ecuación para . ${\ Displaystyle {\ widehat {\ mu}}}$${\ Displaystyle \ sigma}$${\ Displaystyle {\ widehat {\ sigma}} ^ {2}}$

Cuando los valores individuales no están disponibles, pero la media de la muestra y la desviación estándar s sí lo son, los parámetros correspondientes se determinan mediante las siguientes fórmulas, obtenidas al resolver las ecuaciones para la expectativa y la varianza para y : ${\ Displaystyle x_ {1}, x_ {2}, \ ldots, x_ {n}}$${\ displaystyle {\ bar {x}}}$ ${\ Displaystyle \ operatorname {E} [X]}$${\ Displaystyle \ operatorname {Var} [X]}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma}$

${\ Displaystyle \ mu = \ ln \ left ({\ bar {x}} \ {\ Big /} \ {\ sqrt {1 + {\ frac {{\ widehat {\ sigma}} ^ {2}} {{ \ bar {x}} ^ {2}}}}} \ right), \ qquad \ sigma ^ {2} = \ ln \ left (1 + {\ frac {{\ widehat {\ sigma}} ^ {2} } {{\ bar {x}} ^ {2}}} \ right)}$.

Estadísticas

La forma más eficiente de analizar datos distribuidos logarítmicamente normalmente consiste en aplicar los métodos bien conocidos basados ​​en la distribución normal a los datos transformados logarítmicamente y luego volver a transformar los resultados si es apropiado.

Intervalos de dispersión

Los intervalos de dispersión dan un ejemplo básico: para la distribución normal, el intervalo contiene aproximadamente dos tercios (68%) de la probabilidad (o de una muestra grande) y contiene el 95%. Por lo tanto, para una distribución logarítmica normal, ${\ Displaystyle [\ mu - \ sigma, \ mu + \ sigma]}$${\ Displaystyle [\ mu -2 \ sigma, \ mu +2 \ sigma]}$

${\ Displaystyle [\ mu ^ {*} / \ sigma ^ {*}, \ mu ^ {*} \ cdot \ sigma ^ {*}] = [\ mu ^ {*} {} ^ {\ times} \! \! / \ sigma ^ {*}]}$ contiene 2/3, y

${\ Displaystyle [\ mu ^ {*} / (\ sigma ^ {*}) ^ {2}, \ mu ^ {*} \ cdot (\ sigma ^ {*}) ^ {2}] = [\ mu ^ {*} {} ^ {\ times} \! \! / (\ sigma ^ {*}) ^ {2}]}$ contiene 95%

de la probabilidad. Usando parámetros estimados, entonces aproximadamente los mismos porcentajes de los datos deben estar contenidos en estos intervalos.

Intervalo de confianza para ${\ Displaystyle \ mu ^ {*}}$

Utilizando el principio, observe que un intervalo de confianza para es , donde es el error estándar yq es el cuantil del 97,5% de una distribución t con n-1 grados de libertad. La retrotransformación conduce a un intervalo de confianza para , ${\ Displaystyle \ mu}$${\ Displaystyle [{\ widehat {\ mu}} \ pm q \ cdot {\ widehat {\ mathop {se}}}]}$${\ Displaystyle \ mathop {se} = {\ widehat {\ sigma}} / {\ sqrt {n}}}$${\ Displaystyle \ mu ^ {*}}$

${\ Displaystyle [{\ widehat {\ mu}} ^ {*} {} ^ {\ times} \! \! / (\ operatorname {sem} ^ {*}) ^ {q}]}$ con ${\ Displaystyle \ operatorname {sem} ^ {*} = ({\ widehat {\ sigma}} ^ {*}) ^ {1 / {\ sqrt {n}}}}$

Principio extremo de entropía para fijar el parámetro libre. ${\ Displaystyle \ sigma}$

En aplicaciones, es un parámetro por determinar. Para los procesos de crecimiento equilibrados por la producción y la disipación, el uso de un principio extremo de entropía de Shannon muestra que ${\ Displaystyle \ sigma}$

${\ Displaystyle {\ begin {alineado} \ sigma = 1 {\ big /} {\ sqrt {6}} \ end {alineado}}}$

Este valor se puede utilizar para dar alguna relación de escala entre el punto de inflexión y el punto máximo de la distribución log-normal. Esta relación está determinada por la base del logaritmo natural , y exhibe cierta similitud geométrica con el principio de energía superficial mínima. Estas relaciones de escala son útiles para predecir una serie de procesos de crecimiento (propagación de la epidemia, salpicaduras de gotas, crecimiento de la población, velocidad de remolino del vórtice de la bañera, distribución de los caracteres del lenguaje, perfil de velocidad de las turbulencias, etc.). Por ejemplo, la función logarítmica normal con tal encaja bien con el tamaño de las gotas producidas de forma secundaria durante el impacto de las gotas y la propagación de una enfermedad epidémica. ${\ Displaystyle e = 2.718 \ ldots}$${\ Displaystyle \ sigma}$

El valor se usa para proporcionar una solución probabilística para la ecuación de Drake. ${\ Displaystyle \ sigma = 1 {\ big /} {\ sqrt {6}}}$

Ocurrencia y aplicaciones

La distribución logarítmica normal es importante en la descripción de los fenómenos naturales. Muchos procesos de crecimiento natural son impulsados ​​por la acumulación de muchos pequeños cambios porcentuales que se vuelven aditivos en una escala logarítmica. En condiciones de regularidad apropiadas, la distribución de los cambios acumulados resultantes se aproximará cada vez más mediante un log-normal, como se indica en la sección anterior sobre el " Teorema del límite central multiplicativo ". Esto también se conoce como ley de Gibrat , en honor a Robert Gibrat (1904-1980), quien la formuló para las empresas. Si la tasa de acumulación de estos pequeños cambios no varía con el tiempo, el crecimiento se vuelve independiente del tamaño. Incluso si eso no es cierto, las distribuciones de tamaño a cualquier edad de las cosas que crecen con el tiempo tienden a ser logarítmicas normales.

Una segunda justificación se basa en la observación de que las leyes naturales fundamentales implican multiplicaciones y divisiones de variables positivas. Algunos ejemplos son la ley de gravitación simple que conecta masas y distancias con la fuerza resultante, o la fórmula para concentraciones de equilibrio de sustancias químicas en una solución que conecta concentraciones de eductos y productos. Asumir distribuciones log-normales de las variables involucradas conduce a modelos consistentes en estos casos.

Incluso si ninguna de estas justificaciones se aplica, la distribución logarítmica normal es a menudo un modelo plausible y empíricamente adecuado. Los ejemplos incluyen lo siguiente:

Comportamientos humanos

• La longitud de los comentarios publicados en los foros de discusión de Internet sigue una distribución logarítmica normal.
• El tiempo de permanencia de los usuarios en los artículos en línea (bromas, noticias, etc.) sigue una distribución logarítmica normal.
• La duración de las partidas de ajedrez tiende a seguir una distribución logarítmica normal.
• Las duraciones de inicio de los estímulos de comparación acústica que se corresponden con un estímulo estándar siguen una distribución logarítmica normal.
• Las soluciones del cubo de Rubik , tanto generales como personales, parecen seguir una distribución logarítmica normal.

En biología y medicina

• Medidas de tamaño de tejido vivo (longitud, área de piel, peso).
• Para epidemias altamente transmisibles, como el SARS en 2003, si se involucran políticas de control de intervención pública, se muestra que el número de casos hospitalizados satisface la distribución logarítmica normal sin parámetros libres si se asume una entropía y la desviación estándar está determinada por la principio de la tasa máxima de producción de entropía.
• La longitud de los apéndices inertes (pelo, garras, uñas, dientes) de especímenes biológicos, en la dirección de crecimiento.
• El recuento normalizado de RNA-Seq para cualquier región genómica puede aproximarse bien mediante una distribución logarítmica normal.
• La longitud de lectura de secuenciación de PacBio sigue una distribución logarítmica normal.
• Ciertas medidas fisiológicas, como la presión arterial de humanos adultos (después de la separación en subpoblaciones masculinas / femeninas).
• Varias variables farmacocinéticas , como la C _max , la vida media de eliminación y la tasa de eliminación constante .
• En neurociencia, la distribución de las tasas de activación en una población de neuronas suele ser aproximadamente logarítmica normal. Esto se ha observado primero en la corteza y el cuerpo estriado y más tarde en el hipocampo y la corteza entorrinal, y en otras partes del cerebro. Además, las distribuciones de ganancia intrínseca y las distribuciones de peso sinápticas también parecen ser logarítmicas normales.
• En la gestión de quirófanos, la distribución de la duración de la cirugía .

En química coloidal y química de polímeros

• Distribuciones de tamaño de partículas .
• Distribuciones de masa molar .

En consecuencia, los rangos de referencia para las mediciones en individuos sanos se estiman con mayor precisión asumiendo una distribución logarítmica normal que asumiendo una distribución simétrica alrededor de la media.

Distribución logarítmica normal acumulada ajustada a las precipitaciones máximas anuales de 1 día, ver ajuste de distribución

Hidrología

• En hidrología , la distribución logarítmica normal se utiliza para analizar valores extremos de variables tales como los valores máximos mensuales y anuales de las precipitaciones diarias y los volúmenes de descarga de los ríos.

La imagen de la derecha, realizada con CumFreq , ilustra un ejemplo de cómo ajustar la distribución logarítmica normal a las precipitaciones máximas anuales clasificadas en un día, mostrando también el cinturón de confianza del 90% basado en la distribución binomial .

Los datos de lluvia se representan trazando posiciones como parte de un análisis de frecuencia acumulativa .

Ciencias sociales y demografía

• En economía , hay evidencia de que los ingresos del 97% -99% de la población se distribuyen logarítmicamente normal. (La distribución de los individuos de mayores ingresos sigue una distribución de Pareto ).
• Si una distribución del ingreso sigue una distribución logarítmica normal con desviación estándar , entonces el coeficiente de Gini , que se usa comúnmente para evaluar la desigualdad del ingreso, se puede calcular como donde es la función de error , ya que donde es la función de distribución acumulada de una distribución normal estándar.${\ Displaystyle \ sigma}$${\ Displaystyle G = \ operatorname {erf} \ left ({\ frac {\ sigma} {2}} \ right)}$${\ Displaystyle \ operatorname {erf}}$${\ Displaystyle G = 2 \ Phi \ left ({\ frac {\ sigma} {\ sqrt {2}}} \ right) -1}$${\ Displaystyle \ Phi (x)}$
• En finanzas , en particular el modelo Black-Scholes , los cambios en el logaritmo de los tipos de cambio, índices de precios e índices bursátiles se asumen normales (estas variables se comportan como interés compuesto, no como interés simple, y por tanto son multiplicativas). Sin embargo, algunos matemáticos como Benoit Mandelbrot han argumentado que las distribuciones log-Lévy , que poseen colas pesadas , serían un modelo más apropiado, en particular para el análisis de caídas del mercado de valores . De hecho, las distribuciones de los precios de las acciones suelen tener una cola gruesa . La distribución de cola gruesa de los cambios durante las caídas del mercado de valores invalida los supuestos del teorema del límite central .
• En cienciometría , el número de citas a artículos de revistas y patentes sigue una distribución logarítmica normal discreta.
• Los tamaños de las ciudades (población) satisfacen la Ley de Gibrat. El proceso de crecimiento del tamaño de las ciudades es proporcional e invariable con respecto al tamaño. Por lo tanto, a partir del teorema del límite central , el logaritmo del tamaño de la ciudad se distribuye normalmente.

Tecnología

• En el análisis de confiabilidad , la distribución logarítmica normal se usa a menudo para modelar los tiempos para reparar un sistema mantenible.
• En la comunicación inalámbrica , "la potencia media local expresada en valores logarítmicos, como dB o neper, tiene una distribución normal (es decir, gaussiana)". Además, la obstrucción aleatoria de las señales de radio debido a grandes edificios y colinas, denominada sombra , a menudo se modela como una distribución logarítmica normal.
• Distribuciones de tamaño de partículas producidas por trituración con impactos aleatorios, como en el molino de bolas .
• La distribución del tamaño de los archivos de datos de audio y video disponibles públicamente ( tipos MIME ) sigue una distribución logarítmica normal en cinco órdenes de magnitud .
• En redes de computadoras y análisis de tráfico de Internet , logaritmo normal se muestra como un buen modelo estadístico para representar la cantidad de tráfico por unidad de tiempo. Esto se ha demostrado mediante la aplicación de un enfoque estadístico sólido en un gran grupo de rastros reales de Internet. En este contexto, la distribución logarítmica normal ha mostrado un buen desempeño en dos casos de uso principales: (1) predecir la proporción de tiempo que el tráfico excederá un nivel dado (para acuerdo de nivel de servicio o estimación de capacidad de enlace), es decir, dimensionamiento de enlace basado en ancho de banda aprovisionamiento y (2) predicción de precios del percentil 95.

Ver también

• Distribución de cola pesada
• Modelo de pérdida de trayectoria de distancia logarítmica
• Distribución de ley de potencia lognormal modificada
• Desvanecimiento lento

Notas

Otras lecturas

• Cuervo, Edwin L .; Shimizu, Kunio, eds. (1988), Distribuciones lognormales, teoría y aplicaciones , Estadística: libros de texto y monografías, 88 , Nueva York: Marcel Dekker, Inc., págs. Xvi + 387, ISBN 978-0-8247-7803-3, MR  0939191 , Zbl  0.644,62014
• Aitchison, J. y Brown, JAC (1957) The Lognormal Distribution , Cambridge University Press.
• Limpert, E; Stahel, W; Abbt, M (2001). "Distribuciones lognormales en las ciencias: claves y pistas" . BioScience . 51 (5): 341–352. doi : 10.1641 / 0006-3568 (2001) 051 [0341: LNDATS] 2.0.CO; 2 .
• Holgate, P. (1989). "La función característica logarítmica normal". Comunicaciones en estadística: teoría y métodos . 18 (12): 4539–4548. doi : 10.1080 / 03610928908830173 .
• Brooks, Robert; Corson, Jon; Donal, Gales (1994). "El precio de las opciones de índice cuando todos los activos subyacentes siguen una difusión lognormal". Avances en la investigación de futuros y opciones . 7 . SSRN  5735 .

enlaces externos

• La distribución normal es la distribución logarítmica normal