Límite de una función - Limit of a function

Parte de una serie de artículos sobre
Cálculo
Teorema fundamental Regla integral de Leibniz Límites de funciones Continuidad Teorema del valor medio Teorema de rolle
Diferencial Definiciones Derivado  ( generalizaciones ) Diferencial infinitesimal de una función total Conceptos Notación de diferenciación Segunda derivada Diferenciación implícita Diferenciación logarítmica Tarifas relacionadas Teorema de Taylor Reglas e identidades Suma Producto Cadena Poder Cociente Regla de L'Hôpital Inverso General Leibniz La fórmula de Faà di Bruno Reynolds
Integral Listas de integrales Transformada integral Definiciones Antiderivada Integral  ( inadecuado ) Integral de Riemann Integración de Lebesgue Integración de contorno Integral de funciones inversas Integración por Partes Discos Carcasas cilíndricas Sustitución  ( trigonométrica , Weierstrass , Euler ) Fórmula de Euler Fracciones parciales Cambio de orden Fórmulas de reducción Diferenciar bajo el signo integral Algoritmo de Risch
Serie Geométrico  ( aritmético-geométrico ) Armónico Alterno Poder Binomio Taylor Pruebas de convergencia Límite de suma (prueba temporal) Proporción Raíz Integral Comparación directa Límite de comparación Serie alternante Condensación de Cauchy Dirichlet Abel
Vector Degradado Divergencia Rizo Laplaciano Derivado direccional Identidades Teoremas Degradado Verduras Stokes ' Divergencia Stokes generalizado
Multivariable Formalismos Matriz Tensor Exterior Geométrico Definiciones Derivada parcial Integral múltiple Integral de línea Integral de superficie Integral de volumen Jacobiano arpillera
Especializado Fraccionario Malliavin Estocástico Variaciones
Diverso Precálculo Historia Glosario Lista de temas Abeja de integración Análisis
v t mi

En matemáticas , el límite de una función es un concepto fundamental en cálculo y análisis sobre el comportamiento de esa función cerca de una entrada en particular .

Las definiciones formales, concebidas por primera vez a principios del siglo XIX, se dan a continuación. De manera informal, una función f asigna una salida f ( x ) a cada entrada x . Decimos que la función tiene un límite L en una entrada p, si f ( x ) se acerca más y más a L a medida que x se acerca más y más a p . Más específicamente, cuando f se aplica a cualquier entrada suficientemente cerca de p , el valor de salida es forzado arbitrariamente cerca de L . Por otro lado, si algunas entradas muy cercanas ap se llevan a salidas que se mantienen separadas a una distancia fija, entonces decimos que el límite no existe .

La noción de límite tiene muchas aplicaciones en el cálculo moderno . En particular, las muchas definiciones de continuidad emplean el concepto de límite: aproximadamente, una función es continua si todos sus límites concuerdan con los valores de la función. El concepto de límite también aparece en la definición de la derivada : en el cálculo de una variable, este es el valor límite de la pendiente de las líneas secantes a la gráfica de una función.

Historia

Aunque implícita en el desarrollo del cálculo de los siglos XVII y XVIII, la idea moderna del límite de una función se remonta a Bolzano quien, en 1817, introdujo los fundamentos de la técnica épsilon-delta para definir funciones continuas. Sin embargo, su trabajo no se conoció durante su vida.

En su libro de 1821 Cours d'analyse , Cauchy discutió cantidades variables, infinitesimales y límites, y definió la continuidad de diciendo que un cambio infinitesimal en x necesariamente produce un cambio infinitesimal en y , mientras que ( Grabiner 1983 ) afirma que usó una épsilon rigurosa -definición delta en pruebas. Weierstrass introdujo por primera vez la definición de límite épsilon-delta en la forma en que se escribe habitualmente en la actualidad. También introdujo las notaciones lim y lim _{x → x 0} . ${\ Displaystyle y = f (x)}$

La notación moderna de colocar la flecha debajo del símbolo del límite se debe a Hardy , que se presenta en su libro A Course of Pure Mathematics en 1908.

Motivación

Imagina a una persona caminando sobre un paisaje representado por la gráfica de y = f ( x ). Su posición horizontal se mide por el valor de x , al igual que la posición dada por un mapa de la tierra o por un sistema de posicionamiento global . Su altitud viene dada por la coordenada y . Caminan hacia la posición horizontal dada por x = p . A medida que se acerca cada vez más a ella, se dan cuenta de que su altura se aproxima a L . Si se le pregunta acerca de la altitud de x = p , entonces respondería L .

Entonces, ¿qué significa decir que su altitud se acerca a L? Significa que su altitud se acerca cada vez más a L, excepto por un posible pequeño error en la precisión. Por ejemplo, supongamos que fijamos una meta exactitud particular para nuestro viajero: deben acercarse a menos de diez metros de L . Ellos informan que, en efecto, que pueden conseguir dentro de diez metros de desnivel de L , ya que cuenta que cuando están a menos de cincuenta metros horizontales de p , su altitud es siempre metros diez o menos de L .

Luego se cambia el objetivo de precisión: ¿pueden llegar dentro de un metro vertical? Si. Si están en cualquier lugar dentro de los siete metros horizontales de p , su altitud permanecerá siempre dentro de un metro de la meta L . En resumen, decir que la altitud del viajero se acerca a L cuando su posición horizontal se acerca a p , es decir que para cada objetivo de precisión objetivo, por pequeño que sea, hay algún vecindario de p cuya altitud cumple ese objetivo de precisión.

La declaración informal inicial ahora se puede explicar:

El límite de una función f ( x ) cuando x se acerca a p es un número L con la siguiente propiedad: dada cualquier distancia objetivo desde L , hay una distancia desde p dentro de la cual los valores de f ( x ) permanecen dentro de la distancia objetivo.

De hecho, esta declaración explícita se acerca bastante a la definición formal del límite de una función, con valores en un espacio topológico .

Más específicamente, para decir que

${\ Displaystyle \ lim _ {x \ ap} f (x) = L, \,}$

es decir que ƒ ( x ) puede hacerse tan cerca de L como se desee, haciendo x suficientemente cerca, pero no es igual, a  p .

Las siguientes definiciones, conocidas como definiciones (ε, δ), son las definiciones generalmente aceptadas para el límite de una función en varios contextos.

Funciones de una sola variable

(ε, δ) -definición de límite

Supongamos que f  : R → R se define en la recta real y p, L ∈ R . Se diría que el límite de f , cuando x se acerca a p , es L y se escribe

${\ Displaystyle \ lim _ {x \ ap} f (x) = L,}$

o alternativamente como:

${\ Displaystyle f (x) \ a L}$como (lee " tiende a como tiende a ")${\ Displaystyle x \ to p}$${\ Displaystyle f (x)}$${\ Displaystyle L}$${\ Displaystyle x}$${\ Displaystyle p}$

si se cumple la siguiente propiedad:

• Para todo ε > 0 real , existe un δ > 0 real tal que para todo x real, 0 <| x - p | < δ implica que | f ( x ) - L | < ε .

Se aplica una definición más general para las funciones definidas en subconjuntos de la línea real. Sea ( a ,  b ) un intervalo abierto en R , yp un punto de ( a ,  b ). Sea f una función de valor real definida en todo ( a ,  b ), excepto posiblemente en el mismo p . Entonces se dice que el límite de f cuando x se acerca a p es L, si para todo ε > 0 real , existe un δ > 0 real tal que 0 <| x - p | < δ y x ∈ ( a , b ) implica que | f ( x ) - L | < ε .

Aquí, observe que el valor del límite no depende de que f se defina en p , ni del valor f ( p ), si está definido.

Las letras ε y δ pueden entenderse como "error" y "distancia". De hecho, Cauchy usó ε como abreviatura de "error" en algunos de sus trabajos, aunque en su definición de continuidad, usó un infinitesimal en lugar de ε o δ (ver Cours d'Analyse ). En estos términos, el error ( ε ) en la medición del valor en el límite se puede hacer tan pequeño como se desee, reduciendo la distancia ( δ ) al punto límite. Como se analiza a continuación, esta definición también funciona para funciones en un contexto más general. La idea de que δ y ε representan distancias ayuda a sugerir estas generalizaciones. ${\ Displaystyle \ alpha}$

Existencia y límites unilaterales

Alternativamente, x puede acercarse a p desde arriba (derecha) o desde abajo (izquierda), en cuyo caso los límites pueden escribirse como

${\ Displaystyle \ lim _ {x \ ap ^ {+}} f (x) = L}$

o

${\ Displaystyle \ lim _ {x \ ap ^ {-}} f (x) = L}$

respectivamente. Si estos límites existen en p y son iguales allí, entonces esto se puede denominar el límite de f ( x ) en p . Si los límites unilaterales existen en p , pero son desiguales, entonces no hay límite en p (es decir, el límite en p no existe). Si alguno de los límites unilaterales no existe en p , entonces el límite en p tampoco existe.

Una definición formal es la siguiente. El límite de f ( x ) cuando x se acerca a p desde arriba es L si, para todo ε  > 0, existe un δ > 0 tal que | f ( x ) -  L | <  ε siempre que 0 <  x  -  p  <  δ . El límite de f ( x ) cuando x se acerca a p desde abajo es L si, para todo ε > 0, existe un δ > 0 tal que | f ( x ) -  L | <  ε siempre que 0 <  p  -  x  <  δ .

Si el límite no existe, entonces la oscilación de f en p es distinta de cero.

Subconjuntos más generales

Aparte de los intervalos abiertos, se pueden definir límites para funciones en subconjuntos arbitrarios de R , como sigue ( Bartle y Sherbert 2000 ) : sea f una función de valor real definida en un subconjunto S de la línea real. Sea p un punto límite de S , es decir, p es el límite de alguna secuencia de elementos de S distintos de p. El límite de f , cuando x se acerca a p desde los valores en S , es L, si para todo ε > 0 , existe un δ > 0 tal que 0 <| x - p | < δ y x ∈ S implica que | f ( x ) - L | < ε . error de harv: sin destino: CITEREFBartleSherbert2000 ( ayuda )

Este límite a menudo se escribe como:

${\ Displaystyle L = \ lim _ {\ stackrel {x \ ap} {x \ in S}} f (x).}$

La condición de que f se defina en S es que S sea ​​un subconjunto del dominio de f . Esta generalización incluye, como casos especiales, límites en un intervalo, así como límites para zurdos de funciones con valor real (p. Ej., Tomando S como un intervalo abierto de la forma ) y límites para diestros (p. Ej., Tomando S ser un intervalo abierto de la forma ). También extiende la noción de límites unilaterales a los puntos finales incluidos de los intervalos (medio) cerrados, por lo que la función de raíz cuadrada f ( x ) = √ x puede tener un límite 0 cuando x se acerca a 0 desde arriba. ${\ Displaystyle (- \ infty, a)}$${\ Displaystyle (a, \ infty)}$

Límites eliminados versus no eliminados

La definición de límite dada aquí no depende de cómo (o si) se define f en p . Bartle (1967) se refiere a esto como un límite eliminado , porque excluye el valor de f en p . El límite no eliminado correspondiente depende del valor de f en p , si p está en el dominio de f :

• Un número L es el límite no eliminado de f cuando x se acerca a p si, para todo ε > 0 , existe un δ > 0 tal que | x  -  p  | <  Δ y x ∈ Dm ( f ) implica | f ( x ) -  L  | <  ε .

La definición es la misma, excepto que el barrio | x  -  p  | <  δ ahora incluye el punto p , en contraste con la vecindad eliminada 0 <| x  -  p  | <  δ . Esto hace que la definición de un límite no eliminado sea menos general. Una de las ventajas de trabajar con límites no eliminados es que permiten establecer el teorema sobre los límites de las composiciones sin ninguna restricción sobre las funciones (aparte de la existencia de sus límites no eliminados) ( Hubbard (2015) ).

Bartle (1967) señala que, aunque algunos autores se refieren a este límite no eliminado por "límite", los límites eliminados son los más populares. Por ejemplo, Apostol (1974) , Courant (1924) , Hardy (1921) , Rudin (1964) , Whittaker y Watson (1902) todos toman "límite" para significar el límite eliminado. error de harvtxt: sin destino: CITEREFWhittakerWatson1902 ( ayuda )

Ejemplos de

Inexistencia de límites unilaterales

La función

${\ displaystyle f (x) = {\ begin {cases} \ sin {\ frac {5} {x-1}} & {\ text {for}} x <1 \\ 0 & {\ text {for}} x = 1 \\ {\ frac {0.1} {x-1}} & {\ text {for}} x> 1 \ end {cases}}}$

no tiene límite en (el límite de la izquierda no existe debido a la naturaleza oscilatoria de la función seno, y el límite de la derecha no existe debido al comportamiento asintótico de la función recíproca), pero tiene un límite en todos los demás x -coordinate. ${\ Displaystyle x_ {0} = 1}$

La función

${\ displaystyle f (x) = {\ begin {cases} 1 & x {\ text {racional}} \\ 0 & x {\ text {irrational}} \ end {cases}}}$

(también conocida como la función de Dirichlet ) no tiene límite en ninguna coordenada x .

No igualdad de límites unilaterales

La función

${\ displaystyle f (x) = {\ begin {cases} 1 & {\ text {for}} x <0 \\ 2 & {\ text {for}} x \ geq 0 \ end {cases}}}$

tiene un límite en cada coordenada x distinta de cero (el límite es igual a 1 para x negativa e igual a 2 para x positiva ). El límite en x = 0 no existe (el límite de la izquierda es igual a 1, mientras que el límite de la derecha es igual a 2).

Límites en un solo punto

Las funciones

${\displaystyle f(x)={\begin{cases}x&x{\text{ rational }}\\0&x{\text{ irrational }}\end{cases}}}$

y

${\ displaystyle f (x) = {\ begin {cases} | x | & x {\ text {racional}} \\ 0 & x {\ text {irrational}} \ end {cases}}}$

ambos tienen un límite en x = 0 y es igual a 0.

Límites en innumerables puntos

La función

${\ Displaystyle f (x) = {\ begin {cases} \ sin x & x {\ text {irracional}} \\ 1 & x {\ text {racional}} \ end {cases}}}$

tiene un límite en cualquier coordenada x de la forma , donde n es cualquier número entero. ${\ Displaystyle {\ frac {\ pi} {2}} + 2n \ pi}$

Funciones en espacios métricos

Supongamos que M y N son subconjuntos de espacios métricos A y B , respectivamente, y f  : M → N se define entre M y N , con x ∈ M, p un punto límite de M y L ∈ N . Se dice que el límite de f cuando x se acerca a p es L y escribe

${\ Displaystyle \ lim _ {x \ ap} f (x) = L}$

si se cumple la siguiente propiedad:

• Para cada ε> 0, existe un δ> 0 tal que d _B ( f ( x ), L ) <ε siempre que 0 <  d _A ( x ,  p ) <  δ .

Una vez más, nota que p no tiene que ser en el dominio de f , ni L necesidad de estar en la gama de f , e incluso si f ( p se define) no tiene que ser igual a L .

Una definición alternativa que utiliza el concepto de vecindario es la siguiente:

${\ Displaystyle \ lim _ {x \ ap} f (x) = L}$

si, para cada zona V de L en B , existe un entorno U de p en A tal que f (U ∩ M - { p }) ⊆ V .

Funciones en espacios topológicos

Suponga que X , Y son espacios topológicos con Y un espacio de Hausdorff . Deje que p sea un punto límite de Ω ⊆  X , y L ∈ Y . Para una función f  : Ω → Y , se dice que el límite de f cuando x se acerca a p es L (es decir, f ( x ) → L cuando x → p ) y se escribe

${\ Displaystyle \ lim _ {x \ ap} f (x) = L}$

si se cumple la siguiente propiedad:

• Por cada abierto vecindad V de L , existe un entorno abierto U de p tal que f ( U  ∩ Ω - { p }) ⊆ V .

Esta última parte de la definición también puede expresarse "existe una vecindad perforada abierta U de p tal que f ( U ∩Ω) ⊆ V ".

Tenga en cuenta que el dominio de f no necesita contener p . Si es así, entonces el valor de f en p es irrelevante para la definición del límite. En particular, si el dominio de f es X  - { p } (o todo X ), entonces el límite de f cuando x → p existe y es igual a L si, para todos los subconjuntos Ω de X con punto límite p , el límite de la restricción de f a Ω existe y es igual a L . A veces, este criterio se utiliza para establecer la inexistencia del límite bilateral de una función en R mostrando que los límites unilaterales no existen o no concuerdan. Esta visión es fundamental en el campo de la topología general , donde los límites y la continuidad en un punto se definen en términos de familias especiales de subconjuntos, llamados filtros , o secuencias generalizadas conocidas como redes .

Alternativamente, el requisito de que Y sea ​​un espacio de Hausdorff se puede relajar al supuesto de que Y sea ​​un espacio topológico general, pero entonces el límite de una función puede no ser único. En particular, ya no se puede hablar del límite de una función en un punto, sino de un límite o del conjunto de límites en un punto.

Una función es continua en un punto límite p de y en su dominio si y solo si f ( p ) es el (o, en el caso general, a ) límite de f ( x ) cuando x tiende ap .

Límites que involucran el infinito

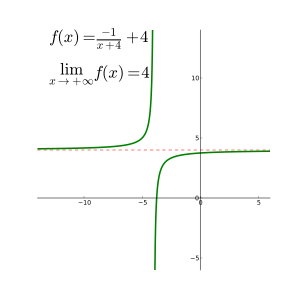
Límites en el infinito

Deja , y . ${\ Displaystyle S \ subseteq \ mathbb {R}}$${\ Displaystyle x \ in S}$${\ Displaystyle f: S \ mapsto \ mathbb {R}}$

El límite de f cuando x se acerca al infinito es L , denotado

${\ Displaystyle \ lim _ {x \ to \ infty} f (x) = L,}$

significa que para todos , existe c tal que siempre que x  >  c . O simbólicamente: ${\ Displaystyle \ varepsilon> 0}$${\ Displaystyle | f (x) -L | <\ varepsilon}$

${\ Displaystyle \ forall \ varepsilon> 0 \; \ existe c \; \ forall x> c: \; | f (x) -L | <\ varepsilon}$.

De manera similar, el límite de f cuando x se acerca al infinito negativo es L , denotado

${\ Displaystyle \ lim _ {x \ to - \ infty} f (x) = L,}$

significa que para todo existe c tal que siempre que x  <  c . O simbólicamente: ${\ Displaystyle \ varepsilon> 0}$${\ Displaystyle | f (x) -L | <\ varepsilon}$

${\ Displaystyle \ forall \ varepsilon> 0 \; \ existe c \; \ forall x <c: \; | f (x) -L | <\ varepsilon}$.

Por ejemplo,

${\ Displaystyle \ lim _ {x \ to - \ infty} e ^ {x} = 0. \,}$

Límites infinitos

Para una función cuyos valores crecen sin límite, la función diverge y el límite habitual no existe. Sin embargo, en este caso se pueden introducir límites con valores infinitos. Deja , y . El enunciado del límite de f cuando x se acerca a a es infinito , denotado ${\ Displaystyle S \ subseteq \ mathbb {R}}$${\ Displaystyle x \ in S}$${\ Displaystyle f: S \ mapsto \ mathbb {R}}$

${\ Displaystyle \ lim _ {x \ to a} f (x) = \ infty,}$

significa que para todo existe tal que siempre que${\ Displaystyle N> 0}$${\ Displaystyle \ delta> 0}$${\ Displaystyle f (x)> N}$${\ Displaystyle 0 <| xa | <\ delta.}$

Estas ideas se pueden combinar de forma natural para producir definiciones para diferentes combinaciones, como

${\ Displaystyle \ lim _ {x \ to \ infty} f (x) = \ infty, \ lim _ {x \ to a ^ {+}} f (x) = - \ infty.}$

Por ejemplo,

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} \ ln x = - \ infty.}$

Los límites que involucran infinito están conectados con el concepto de asíntotas .

Estas nociones de límite intentan proporcionar una interpretación del espacio métrico hasta los límites en el infinito. De hecho, son consistentes con la definición de límite de espacio topológico si

• una vecindad de −∞ se define para contener un intervalo [−∞,  c ) para algún c  ∈  R ,
• una vecindad de ∞ se define para contener un intervalo ( c , ∞] donde c  ∈  R , y
• un barrio de una ∈ R se define en el espacio métrico forma normal R .

En este caso, R es un espacio topológico y cualquier función de la forma f :  X  →  Y con X ,  Y ⊆  R está sujeta a la definición topológica de un límite. Tenga en cuenta que con esta definición topológica, es fácil definir límites infinitos en puntos finitos, que no se han definido anteriormente en el sentido métrico.

Notación alternativa

Muchos autores permiten que la línea real extendida proyectivamente se utilice como una forma de incluir valores infinitos, así como la línea real extendida . Con esta notación, la línea real extendida se da como R ∪ {−∞, + ∞} y la línea real extendida proyectivamente es R  ∪ {∞} donde una vecindad de ∞ es un conjunto de la forma { x : | x | > c }. La ventaja es que solo se necesitan tres definiciones de límites (izquierda, derecha y central) para cubrir todos los casos. Como se presentó anteriormente, para una explicación completamente rigurosa, necesitaríamos considerar 15 casos separados para cada combinación de infinitos (cinco direcciones: −∞, izquierda, central, derecha y + ∞; tres límites: −∞, finito o + ∞). También hay escollos dignos de mención. Por ejemplo, cuando se trabaja con la línea real extendida, no posee un límite central (lo cual es normal): ${\ displaystyle x ^ {- 1}}$

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} {1 \ over x} = + \ infty, \ lim _ {x \ to 0 ^ {-}} {1 \ over x} = - \ infty .}$

Por el contrario, cuando se trabaja con la recta real proyectiva, infinitos (muy parecido a 0) no están firmados, así, el límite central hace existir en ese contexto:

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} {1 \ over x} = \ lim _ {x \ to 0 ^ {-}} {1 \ over x} = \ lim _ {x \ to 0} {1 \ over x} = \ infty.}$

De hecho, hay una plétora de sistemas formales en conflicto en uso. En determinadas aplicaciones de diferenciación e integración numérica es conveniente, por ejemplo, tener ceros con signo . Una razón simple tiene que ver con lo contrario , es decir, es conveniente que se considere verdadero. Estos ceros pueden verse como una aproximación a infinitesimales . ${\ Displaystyle \ lim _ {x \ to 0 ^ {-}} {x ^ {- 1}} = - \ infty}$${\ Displaystyle \ lim _ {x \ to - \ infty} {x ^ {- 1}} = - 0}$

Límites en el infinito para funciones racionales

Hay tres reglas básicas para la evaluación de los límites en el infinito para una función racional f ( x ) = p ( x ) / q ( x ): (en la que p y q son polinomios):

• Si el grado de p es mayor que el grado de q , entonces el límite es infinito positivo o negativo dependiendo de los signos de los coeficientes principales;
• Si el grado de p y q son iguales, el límite es el coeficiente principal de p dividida por el coeficiente principal de q ;
• Si el grado de p es menor que el grado de q , el límite es 0.

Si existe el límite en el infinito, que representa una asíntota horizontal en y = L . Los polinomios no tienen asíntotas horizontales; Sin embargo, tales asíntotas pueden ocurrir con funciones racionales.

Funciones de más de una variable

Tomando nota de que | x  -  p | representa una distancia, la definición de un límite puede extenderse a funciones de más de una variable. En el caso de una función f  : R ² → R ,

${\ Displaystyle \ lim _ {(x, y) \ to (p, q)} f (x, y) = L}$

si

para todo ε > 0 existe un δ> 0 tal que para todo ( x , y ) con 0 <|| ( x , y ) - ( p , q ) || <δ, entonces | f ( x , y ) -  L | <ε

donde || ( x , y ) - ( p , q ) || representa la distancia euclidiana . Esto se puede extender a cualquier número de variables.

Límites secuenciales

Deje f  : X → Y sea un mapeo desde un espacio topológico X en un espacio de Hausdorff Y , p ∈ X un punto de límite X y L ∈ Y .

El límite secuencial de f como x tiende a p es L si, para cada secuencia ( x _n ) en X - { p } que converge a p , la secuencia de f ( x _n ) converge a L .

Si L es el límite (en el sentido anterior) de f cuando x se acerca a p , entonces también es un límite secuencial; sin embargo, no es necesario que lo contrario se mantenga en general. Si además X es metrizable , entonces L es el límite secuencial de f cuando x se acerca a p si y solo si es el límite (en el sentido anterior) de f cuando x se acerca a p .

Otras caracterizaciones

En términos de secuencias

Para funciones en la línea real, una forma de definir el límite de una función es en términos del límite de sucesiones. (Esta definición generalmente se atribuye a Eduard Heine ). En este contexto:

${\ Displaystyle \ lim _ {x \ to a} f (x) = L}$

si, y solo si, para todas las secuencias (con no igual a a para todos los n ) que convergen a la secuencia converge a . Sierpiński demostró en 1916 que probar la equivalencia de esta definición y la definición anterior requiere y es equivalente a una forma débil del axioma de elección . Tenga en cuenta que definir lo que significa que una secuencia converja requiere el método épsilon, delta . ${\ Displaystyle x_ {n}}$${\ Displaystyle x_ {n}}$${\ Displaystyle a}$${\ Displaystyle f (x_ {n})}$${\ Displaystyle L}$${\ Displaystyle x_ {n}}$${\ Displaystyle a}$

De manera similar, como fue el caso de la definición de Weierstrass, una definición de Heine más general se aplica a las funciones definidas en subconjuntos de la línea real. Sea f una función de valor real con el dominio Dm ( f ). Sea a el límite de una secuencia de elementos de Dm ( f ) \ { a }. Entonces el límite (en este sentido) de f es L cuando x se acerca a p si para cada secuencia  ∈  Dm ( f ) \ { a } (de modo que para todo n , no es igual a a ) que converge a a , la secuencia converge a . Esta es la misma que la definición de un límite secuencial en la sección anterior obtenida al considerar el subconjunto Dm ( f ) de R como un espacio métrico con la métrica inducida. ${\ Displaystyle x_ {n}}$${\ Displaystyle x_ {n}}$${\ Displaystyle f (x_ {n})}$${\ Displaystyle L}$

En cálculo no estándar

En cálculo no estándar, el límite de una función está definido por:

${\ Displaystyle \ lim _ {x \ to a} f (x) = L}$

si y solo si para todos , es infinitesimal siempre que sea ​​infinitesimal. Aquí están los números hiperreales y es la extensión natural de f a los números reales no estándar. Keisler demostró que tal definición hiperreal de límite reduce la complejidad del cuantificador en dos cuantificadores. Por otro lado, Hrbacek escribe que para que las definiciones sean válidas para todos los números hiperreales deben estar implícitamente basadas en el método ε-δ, y afirma que, desde el punto de vista pedagógico, la esperanza de que el cálculo no estándar pueda ser hecho sin los métodos ε-δ no se puede realizar en su totalidad. Bŀaszczyk y col. detallan la utilidad de la microcontinuidad en el desarrollo de una definición transparente de continuidad uniforme y caracterizan la crítica de Hrbacek como un "lamento dudoso". ${\ Displaystyle x \ in \ mathbb {R} ^ {*}}$${\ Displaystyle f ^ {*} (x) -L}$${\ Displaystyle xa}$${\ Displaystyle \ mathbb {R} ^ {*}}$${\ Displaystyle f ^ {*}}$

En términos de cercanía

En el congreso internacional de matemáticas de 1908, F. Riesz introdujo una forma alternativa de definir límites y continuidad en el concepto llamado "cercanía". Un punto se define para estar cerca de un conjunto si para cada hay un punto de modo que . En este escenario el ${\ Displaystyle x}$${\ Displaystyle A \ subseteq \ mathbb {R}}$${\ Displaystyle r> 0}$${\ Displaystyle a \ in A}$${\ Displaystyle | xa | <r}$

${\ Displaystyle \ lim _ {x \ to a} f (x) = L}$

si y solo si para todos , está cerca siempre que esté cerca . Aquí está el set . Esta definición también se puede extender a espacios métricos y topológicos. ${\ Displaystyle A \ subseteq \ mathbb {R}}$${\ Displaystyle L}$${\ Displaystyle f (A)}$${\ Displaystyle a}$${\ Displaystyle A}$${\ Displaystyle f (A)}$${\ Displaystyle \ {f (x) | x \ in A \}}$

Relación con la continuidad

La noción de límite de una función está muy relacionada con el concepto de continuidad. Se dice que una función f es continua en c si está definida en c y su valor en c es igual al límite de f cuando x se acerca a c :

${\ Displaystyle \ lim _ {x \ to c} f (x) = f (c).}$

(Hemos asumido aquí que c es un punto límite del dominio de f .)

Propiedades

Si una función f se valora real, entonces el límite de f en p es L si y sólo si tanto el límite de la mano derecha y el límite de la mano izquierda de f en p existen y son iguales a L .

La función f es continua en p si y solo si el límite de f ( x ) cuando x se acerca a p existe y es igual af ( p ). Si f  : M → N es una función entre los espacios métricos M y N , entonces es equivalente que f transforme cada secuencia en M que converge hacia p en una secuencia en N que converge hacia f ( p ).

Si N es un espacio vectorial normalizado , entonces la operación límite es lineal en el siguiente sentido: si el límite de f ( x ) cuando x se acerca a p es L y el límite de g ( x ) cuando x se acerca a p es P , entonces el límite de f ( x ) + g ( x ) como x se acerca p es L + P . Si a es un escalar del campo base , entonces el límite de af ( x ) cuando x se acerca a p es aL .

Si f y g se valoran real (o de valor complejo) funciones, a continuación, tomando el límite de una operación en f ( x ) y g ( x ) (por ejemplo, , , , , ) bajo ciertas condiciones es compatible con la operación de límites de f (x) y g (x) . Este hecho a menudo se denomina teorema del límite algebraico . La principal condición necesaria para aplicar las siguientes reglas es que existan los límites en el lado derecho de las ecuaciones (en otras palabras, estos límites son valores finitos, incluido 0). Además, la identidad para la división requiere que el denominador del lado derecho sea distinto de cero (la división por 0 no está definida), y la identidad para la exponenciación requiere que la base sea positiva o cero mientras que el exponente sea positivo (finito ). ${\ Displaystyle f + g}$ ${\ displaystyle fg}$ ${\ Displaystyle f \ times g}$ ${\ displaystyle f / g}$ ${\ Displaystyle f ^ {g}}$

${\ Displaystyle {\ begin {matrix} \ lim \ limits _ {x \ to p} & (f (x) + g (x)) & = & \ lim \ limits _ {x \ to p} f (x) + \ lím \ límites _ {x \ ap} g (x) \\\ lím \ límites _ {x \ ap} & (f (x) -g (x)) & = & \ lim \ límites _ { x \ ap} f (x) - \ lim \ limites _ {x \ ap} g (x) \\\ lim \ limites _ {x \ to p} & (f (x) \ cdot g (x) ) & = & \ lim \ limits _ {x \ to p} f (x) \ cdot \ lim \ limits _ {x \ to p} g (x) \\\ lim \ limits _ {x \ to p} & (f (x) / g (x)) & = & {\ lim \ limits _ {x \ to p} f (x) / \ lim \ limits _ {x \ to p} g (x)} \\\ lím \ límites _ {x \ ap} & f (x) ^ {g (x)} & = & {\ lim \ límites _ {x \ ap} f (x) ^ {\ lim \ límites _ {x \ ap} g (x)}} \ end {matriz}}}$

Estas reglas también son válidas para límites unilaterales, incluso cuando p es ∞ o −∞. En cada regla anterior, cuando uno de los límites de la derecha es ∞ o −∞, el límite de la izquierda a veces aún puede estar determinado por las siguientes reglas.

• q + ∞ = ∞ si q ≠ −∞
• q × ∞ = ∞ si q > 0
• q × ∞ = −∞ si q <0
• q / ∞ = 0 si q ≠ ∞ y q ≠ −∞
• ∞ ^q = 0 si q <0
• ∞ ^q = ∞ si q > 0
• q ^∞ = 0 si 0 < q <1
• q ^∞ = ∞ si q > 1
• q ^−∞ = ∞ si 0 < q <1
• q ^−∞ = 0 si q > 1

(ver también Recta numérica real extendida ).

En otros casos, el límite de la izquierda todavía puede existir, aunque el lado derecho, llamado forma indeterminada , no permite determinar el resultado. Esto depende de las funciones f y g . Estas formas indeterminadas son:

• 0/0
• ± ∞ / ± ∞
• 0 × ± ∞
• ∞ + −∞
• 0 ⁰
• ∞ ⁰
• 1 ^{± ∞}

Consulte más abajo la regla de L'Hôpital y la forma indeterminada .

Límites de composición de funciones.

En general, de saber que

${\ Displaystyle \ lim _ {y \ to b} f (y) = c}$y ,${\ Displaystyle \ lim _ {x \ to a} g (x) = b}$

sí no se sigue que . Sin embargo, esta "regla de la cadena" se cumple si se cumple una de las siguientes condiciones adicionales : ${\ Displaystyle \ lim _ {x \ to a} f (g (x)) = c}$

• f ( b ) = c (es decir, f es continua en b ), o
• g no toma el valor b cerca de a (es decir, existe tal que si entonces ).${\ Displaystyle \ delta> 0}$${\ Displaystyle 0 <| xa | <\ delta}$${\ Displaystyle | g (x) -b |> 0}$

Como ejemplo de este fenómeno, considere las siguientes funciones que violan ambas restricciones adicionales:

${\ displaystyle f (x) = g (x) = {\ begin {cases} 0 & {\ text {if}} x \ neq 0 \\ 1 & {\ text {if}} x = 0 \ end {cases}} .}$

Dado que el valor en f (0) es una discontinuidad removible ,

${\ Displaystyle \ lim _ {x \ to a} f (x) = 0}$para todos .${\ Displaystyle a}$

Por lo tanto, la regla de la cadena ingenua sugeriría que el límite de f ( f ( x )) es 0. Sin embargo, se da el caso de que

${\ displaystyle f (f (x)) = {\ begin {cases} 1 & {\ text {if}} x \ neq 0 \\ 0 & {\ text {if}} x = 0 \ end {cases}}}$

y entonces

${\ Displaystyle \ lim _ {x \ to a} f (f (x)) = 1}$para todos .${\ Displaystyle a}$

Límites de especial interés

Funciones racionales

Para un entero no negativo y constantes y , ${\ Displaystyle n}$${\ Displaystyle a_ {1}, a_ {2}, a_ {3}, \ ldots, a_ {n}}$${\ Displaystyle b_ {1}, b_ {2}, b_ {3}, \ ldots, b_ {n}}$

• ${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {a_ {1} {x} ^ {n} + a_ {2} {x} ^ {n-1} + a_ {3} {x} ^ {n-2} + ... + a_ {n}} {b_ {1} {x} ^ {n} + b_ {2} {x} ^ {n-1} + b_ {3} {x} ^ {n-2} + ... + b_ {n}}} = {\ frac {a_ {1}} {b_ {1}}}}$

Esto se puede demostrar dividiendo tanto el numerador como el denominador por . Si el numerador es un polinomio de mayor grado, el límite no existe. Si el denominador es de grado superior, el límite es 0. ${\ Displaystyle x ^ {n}}$

Funciones trigonométricas

• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {\ sin x} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {1- \ cos x} {x}} = 0}$

Funciones exponenciales

• ${\ Displaystyle \ lim _ {x \ to 0} (1 + x) ^ {\ frac {1} {x}} = \ lim _ {r \ to \ infty} \ left (1 + {\ frac {1} {r}} \ right) ^ {r} = e}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {e ^ {x} -1} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {e ^ {ax} -1} {bx}} = {\ frac {a} {b}}}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {c ^ {ax} -1} {bx}} = {\ frac {a} {b}} \ ln c}$
• ${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x ^ {x} = 1}$

Funciones logarítmicas

• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {\ ln (1 + x)} {x}} = 1}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {\ ln (1 + ax)} {bx}} = {\ frac {a} {b}}}$
• ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {\ log _ {c} (1 + ax)} {bx}} = {\ frac {a} {b \ ln c}}}$

Regla de L'Hôpital

Esta regla usa derivadas para encontrar límites de formas indeterminadas 0/0 o ± ∞ / ∞ , y solo se aplica a tales casos. Otras formas indeterminadas pueden manipularse en esta forma. Dadas dos funciones f ( x ) y g ( x ) , definidas sobre un intervalo abierto I que contiene el punto límite deseado c , entonces si:

1. ${\ Displaystyle \ lim _ {x \ to c} f (x) = \ lim _ {x \ to c} g (x) = 0,}$ o , y${\ Displaystyle \ lim _ {x \ to c} f (x) = \ pm \ lim _ {x \ to c} g (x) = \ pm \ infty}$
2. ${\ Displaystyle f}$y son diferenciables sobre , y${\ Displaystyle g}$${\ Displaystyle I \ setminus \ {c \}}$
3. ${\ Displaystyle g '(x) \ neq 0}$para todos , y${\ Displaystyle x \ in I \ setminus \ {c \}}$
4. ${\ Displaystyle \ lim _ {x \ to c} {\ frac {f '(x)} {g' (x)}}}$ existe

luego:

${\ Displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to c} {\ frac {f '(x)} {g '(X)}}}$

Normalmente, la primera condición es la más importante.

Por ejemplo: ${\ Displaystyle \ lim _ {x \ to 0} {\ frac {\ sin (2x)} {\ sin (3x)}} = \ lim _ {x \ to 0} {\ frac {2 \ cos (2x) } {3 \ cos (3x)}} = {\ frac {2 \ cdot 1} {3 \ cdot 1}} = {\ frac {2} {3}}.}$

Sumas e integrales

Especificar un límite infinito en una suma o integral es una forma abreviada común de especificar un límite.

Una forma corta de escribir el límite es . Un ejemplo importante de límites de sumas como estos son las series . ${\ Displaystyle \ lim _ {n \ to \ infty} \ sum _ {i = s} ^ {n} f (i)}$${\ Displaystyle \ sum _ {i = s} ^ {\ infty} f (i)}$

Una forma corta de escribir el límite es . ${\ Displaystyle \ lim _ {x \ to \ infty} \ int _ {a} ^ {x} f (t) \; dt}$${\ Displaystyle \ int _ {a} ^ {\ infty} f (t) \; dt}$

Una forma corta de escribir el límite es . ${\ Displaystyle \ lim _ {x \ to - \ infty} \ int _ {x} ^ {b} f (t) \; dt}$${\ Displaystyle \ int _ {- \ infty} ^ {b} f (t) \; dt}$

Ver también

• Notación Big O  : notación que describe el comportamiento limitante
• Regla de L'Hôpital: regla  matemática para evaluar ciertos límites
• Lista de límites  - artículo de la lista de Wikipedia
• Límite de una secuencia  : valor al que "tienden" los términos de una secuencia.
• Límite superior y límite inferior
• Net (matemáticas)  : una generalización de una secuencia de puntos
• Cálculo no estándar
• Teorema de compresión  : sobre el cálculo de límites al delimitar una función entre otras dos funciones
• Límite subsecuente  : el límite de alguna subsecuencia

Notas

Referencias

• Apostol, Tom M. (1974), Análisis matemático (2 ed.), Addison-Wesley, ISBN 0-201-00288-4
• Bartle, Robert (1967), Los elementos del análisis real , Wiley
• Courant, Richard (1924), Vorlesungen über Differential- und Integralrechnung , Springer Verlag
• Hardy, GH (1921), Un curso de matemáticas puras , Cambridge University Press
• Hubbard, John H. (2015), Cálculo vectorial, álgebra lineal y formas diferenciales: un enfoque unificado (Quinta ed.), Matrix Editions
• Page, Warren; Hersh, Rubén; Selden, Annie; et al., eds. (2002), "Media Highlights", The College Mathematics , 33 (2): 147-154, JSTOR  2687124.
• Rudin, Walter (1964), Principios del análisis matemático , McGraw-Hill
• Sutherland, WA (1975), Introducción a los espacios métricos y topológicos , Oxford: Oxford University Press, ISBN 0-19-853161-3
• Sherbert, Robert (2000), Introducción al análisis real , Wiley
• Whittaker ; Watson (1904), Un curso de análisis moderno , Cambridge University Press

enlaces externos

• MacTutor Historia de Weierstrass.
• MacTutor Historia de Bolzano
• Cálculo visual por Lawrence S. Husch , Universidad de Tennessee (2001)