Cubo de Hilbert - Hilbert cube

En matemáticas , el cubo de Hilbert , llamado así por David Hilbert , es un espacio topológico que proporciona un ejemplo instructivo de algunas ideas en topología . Además, muchos espacios topológicos interesantes se pueden incrustar en el cubo de Hilbert; es decir, pueden verse como subespacios del cubo de Hilbert (ver más abajo).

Definición

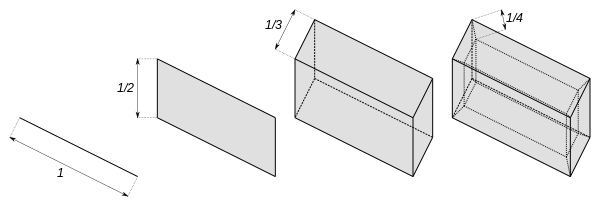
El cubo de Hilbert se define mejor como el producto topológico de los intervalos [0, 1 / n ] para n  = 1, 2, 3, 4, ... Es decir, es un cuboide de dimensión infinita numerable , donde las longitudes de los bordes en cada dirección ortogonal forman la secuencia . ${\ Displaystyle \ lbrace 1 / n \ rbrace _ {n \ in \ mathbb {N}}}$

El cubo de Hilbert es homeomorfo al producto de un número infinito de copias del intervalo unitario [0, 1]. En otras palabras, es topológicamente indistinguible del cubo unitario de dimensión numerablemente infinita.

Si un punto en el cubo de Hilbert se especifica mediante una secuencia con , entonces un homeomorfismo al cubo de la unidad de dimensión infinita viene dado por . ${\ Displaystyle \ lbrace a_ {n} \ rbrace}$${\ Displaystyle 0 \ leq a_ {n} \ leq 1 / n}$${\ Displaystyle h (a) _ {n} = n \ cdot a_ {n}}$

El cubo de Hilbert como espacio métrico

A veces es conveniente pensar en el cubo de Hilbert como un espacio métrico , de hecho como un subconjunto específico de un espacio de Hilbert separable (es decir, un espacio de Hilbert con una base de Hilbert numerablemente infinita). A estos efectos, es mejor no pensar en él como un producto de copias de [0,1], sino como

[0,1] × [0,1 / 2] × [0,1 / 3] × ···;

como se indicó anteriormente, para las propiedades topológicas, esto no hace ninguna diferencia. Es decir, un elemento del cubo de Hilbert es una secuencia infinita

( x _n )

que satisface

0 ≤ x _n ≤ 1 / n .

Cualquier secuencia de este tipo pertenece al espacio de Hilbert ℓ ₂ , por lo que el cubo de Hilbert hereda una métrica de allí. Se puede demostrar que la topología inducida por la métrica es la misma que la topología del producto en la definición anterior.

Propiedades

Como producto de espacios compactos de Hausdorff , el cubo de Hilbert es en sí mismo un espacio compacto de Hausdorff como resultado del teorema de Tychonoff . La compacidad del cubo de Hilbert también se puede demostrar sin el axioma de elección mediante la construcción de una función continua a partir del conjunto de Cantor habitual en el cubo de Hilbert.

En ℓ ₂ , ningún punto tiene una vecindad compacta (por lo tanto, ℓ ₂ no es localmente compacto ). Uno podría esperar que todos los subconjuntos compactos de ℓ ₂ sean de dimensión finita. El cubo de Hilbert muestra que este no es el caso. Pero el cubo de Hilbert no es una vecindad de ningún punto p porque su lado se vuelve cada vez más pequeño en cada dimensión, de modo que una bola abierta alrededor de p de cualquier radio fijo e > 0 debe salir del cubo en alguna dimensión.

Cualquier subconjunto compacto convexo de dimensión infinita de es homeomorfo al cubo de Hilbert. El cubo de Hilbert es un conjunto convexo, cuyo tramo es todo el espacio, pero cuyo interior está vacío. Esta situación es imposible en dimensiones finitas. El cono tangente al cubo en el vector cero es todo el espacio. ${\ Displaystyle l_ {2}}$

Cada subconjunto del cubo de Hilbert hereda del cubo de Hilbert las propiedades de ser metrizable (y por lo tanto T4 ) y segundo contable . Es más interesante que lo contrario también sea válido: cada segundo espacio T4 contable es homeomórfico a un subconjunto del cubo de Hilbert.

Cada subconjunto G _δ del cubo de Hilbert es un espacio polaco , un espacio topológico homeomorfo a un espacio métrico completo y separable. Por el contrario, cada espacio polaco es homeomorfo a un subconjunto G _δ del cubo de Hilbert.

Notas

Referencias

• Srivastava, Shashi Mohan (1998). Un curso sobre conjuntos de Borel . Textos de Posgrado en Matemáticas . Springer-Verlag . ISBN   978-0-387-98412-4 . Consultado el 4 de diciembre de 2008 .
• "Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum" [El homomorfismo de los conjuntos convexos compactos en el espacio de Hilbert] (en alemán). EUDML. Archivado desde el original el 2 de marzo de 2020.

Otras lecturas

• Steen, Lynn Arthur ; Seebach, J. Arthur Jr. (1995) [1978]. Contraejemplos en topología ( reimpresión de Dover de 1978 ed.). Berlín, Nueva York: Springer-Verlag . ISBN   978-0-486-68735-3 . Señor   0507446 .