Descenso de gradiente - Gradient descent

Reproducir medios

Descenso de gradiente en 2D

El descenso de gradiente es un algoritmo de optimización iterativo de primer orden para encontrar un mínimo local de una función diferenciable . La idea es dar pasos repetidos en la dirección opuesta al gradiente (o gradiente aproximado) de la función en el punto actual, porque esta es la dirección de descenso más pronunciado. A la inversa, dar un paso en la dirección del gradiente conducirá a un máximo local de esa función; el procedimiento se conoce como ascenso en pendiente .

El descenso del gradiente se atribuye generalmente a Cauchy , quien lo sugirió por primera vez en 1847. Hadamard propuso de forma independiente un método similar en 1907. Sus propiedades de convergencia para problemas de optimización no lineal fueron estudiadas por primera vez por Haskell Curry en 1944, y el método se volvió cada vez más estudiado. y utilizado en las décadas siguientes, también llamado a menudo descenso más empinado.

Descripción

Ilustración de descenso de gradiente en una serie de conjuntos de niveles

El descenso de gradiente se basa en la observación de que si la función multivariable está definida y es diferenciable en una vecindad de un punto , entonces disminuye más rápido si se va en la dirección del gradiente negativo de en . De ello se deduce que, si ${\ Displaystyle F (\ mathbf {x})}$${\ Displaystyle \ mathbf {a}}$${\ Displaystyle F (\ mathbf {x})}$${\ Displaystyle \ mathbf {a}}$${\ Displaystyle F}$${\ Displaystyle \ mathbf {a}, - \ nabla F (\ mathbf {a})}$

${\ Displaystyle \ mathbf {a} _ {n + 1} = \ mathbf {a} _ {n} - \ gamma \ nabla F (\ mathbf {a} _ {n})}$

por lo suficientemente pequeño, entonces . En otras palabras, el término se resta porque queremos movernos contra el gradiente, hacia el mínimo local. Con esta observación en mente, uno comienza con una suposición de un mínimo local de y considera la secuencia tal que ${\ Displaystyle \ gamma \ in \ mathbb {R} _ {+}}$${\ Displaystyle F (\ mathbf {a_ {n}}) \ geq F (\ mathbf {a_ {n + 1}})}$${\ Displaystyle \ gamma \ nabla F (\ mathbf {a})}$${\ Displaystyle \ mathbf {a}}$${\ Displaystyle \ mathbf {x} _ {0}}$${\ Displaystyle F}$${\ Displaystyle \ mathbf {x} _ {0}, \ mathbf {x} _ {1}, \ mathbf {x} _ {2}, \ ldots}$

${\ Displaystyle \ mathbf {x} _ {n + 1} = \ mathbf {x} _ {n} - \ gamma _ {n} \ nabla F (\ mathbf {x} _ {n}), \ n \ geq 0.}$

Tenemos una secuencia monótona

${\ Displaystyle F (\ mathbf {x} _ {0}) \ geq F (\ mathbf {x} _ {1}) \ geq F (\ mathbf {x} _ {2}) \ geq \ cdots,}$

por lo que, con suerte, la secuencia converge al mínimo local deseado. Tenga en cuenta que se permite que el valor del tamaño del paso cambie en cada iteración. Con ciertas suposiciones sobre la función (por ejemplo, convexa y Lipschitz ) y opciones particulares de (p. Ej., Elegidas mediante una búsqueda de línea que satisfaga las condiciones de Wolfe , o el método de Barzilai-Borwein que se muestra a continuación), ${\ Displaystyle (\ mathbf {x} _ {n})}$ ${\ Displaystyle \ gamma}$${\ Displaystyle F}$${\ Displaystyle F}$ ${\ Displaystyle \ nabla F}$ ${\ Displaystyle \ gamma}$

${\ Displaystyle \ gamma _ {n} = {\ frac {\ left | \ left (\ mathbf {x} _ {n} - \ mathbf {x} _ {n-1} \ right) ^ {T} \ left [\ nabla F (\ mathbf {x} _ {n}) - \ nabla F (\ mathbf {x} _ {n-1}) \ derecha] \ derecha |} {\ izquierda \ | \ nabla F (\ mathbf {x} _ {n}) - \ nabla F (\ mathbf {x} _ {n-1}) \ right \ | ^ {2}}}}$

se puede garantizar la convergencia a un mínimo local. Cuando la función es convexa , todos los mínimos locales también son mínimos globales, por lo que en este caso el descenso del gradiente puede converger a la solución global. ${\ Displaystyle F}$

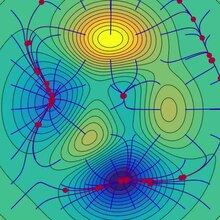
Este proceso se ilustra en la imagen adyacente. Aquí, se supone que está definido en el plano y que su gráfico tiene forma de cuenco . Las curvas azules son las curvas de nivel , es decir, las regiones en las que el valor de es constante. Una flecha roja que se origina en un punto muestra la dirección del gradiente negativo en ese punto. Tenga en cuenta que el gradiente (negativo) en un punto es ortogonal a la línea de contorno que pasa por ese punto. Vemos que el descenso de gradiente nos lleva al fondo del cuenco, es decir, al punto donde el valor de la función es mínimo. ${\ Displaystyle F}$${\ Displaystyle F}$${\ Displaystyle F}$

Una analogía para comprender el descenso de gradientes

Niebla en las montañas

La intuición básica detrás del descenso de gradientes puede ilustrarse mediante un escenario hipotético. Una persona está atrapada en las montañas y está tratando de bajar (es decir, tratando de encontrar el mínimo global). Hay una densa niebla que hace que la visibilidad sea extremadamente baja. Por lo tanto, el camino de bajada de la montaña no es visible, por lo que deben usar la información local para encontrar el mínimo. Pueden usar el método de descenso en gradiente, que implica mirar la pendiente de la colina en su posición actual y luego proceder en la dirección con el descenso más empinado (es decir, cuesta abajo). Si estuvieran tratando de encontrar la cima de la montaña (es decir, el máximo), entonces continuarían en la dirección del ascenso más empinado (es decir, cuesta arriba). Usando este método, eventualmente encontrarían su camino hacia abajo de la montaña o posiblemente se atascarían en algún agujero (es decir, el mínimo local o punto de silla ), como un lago de montaña. Sin embargo, suponga también que la pendiente de la colina no es inmediatamente obvia con una simple observación, sino que requiere un instrumento sofisticado para medir, que la persona tiene en ese momento. Se necesita bastante tiempo para medir la pendiente de la colina con el instrumento, por lo que deben minimizar el uso del instrumento si quieren bajar de la montaña antes de la puesta del sol. La dificultad entonces es elegir la frecuencia con la que deben medir la pendiente de la colina para no salirse de la pista.

En esta analogía, la persona representa el algoritmo y el camino recorrido por la montaña representa la secuencia de ajustes de parámetros que explorará el algoritmo. La pendiente de la colina representa la pendiente de la superficie de error en ese punto. El instrumento utilizado para medir la pendiente es la diferenciación (la pendiente de la superficie de error se puede calcular tomando la derivada de la función de error al cuadrado en ese punto). La dirección en la que eligen viajar se alinea con el gradiente de la superficie de error en ese punto. La cantidad de tiempo que viajan antes de tomar otra medida es el tamaño del paso.

Ejemplos de

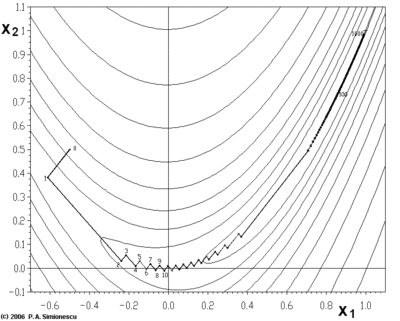
El gradiente de descenso tiene problemas con funciones patológicas como la función de Rosenbrock que se muestra aquí.

${\ Displaystyle f (x_ {1}, x_ {2}) = (1-x_ {1}) ^ {2} +100 (x_ {2} -x_ {1} ^ {2}) ^ {2}. }$

La función Rosenbrock tiene un estrecho valle curvo que contiene el mínimo. El fondo del valle es muy plano. Debido al valle plano curvo, la optimización se realiza en zigzag lentamente con pasos pequeños hacia el mínimo. El latigazo cervical pendiente de descenso resuelve este problema en particular.

La naturaleza en zigzag del método también es evidente a continuación, donde el método de descenso de gradiente se aplica a

${\ Displaystyle F (x, y) = \ sin \ left ({\ frac {1} {2}} x ^ {2} - {\ frac {1} {4}} y ^ {2} +3 \ right ) \ cos \ left (2x + 1-e ^ {y} \ right).}$

Elegir el tamaño del paso y la dirección de descenso

Dado que el uso de un tamaño de paso demasiado pequeño ralentizaría la convergencia y uno demasiado grande conduciría a la divergencia, encontrar un buen ajuste de es un problema práctico importante. Philip Wolfe también abogó por utilizar "elecciones inteligentes de la dirección [de descenso]" en la práctica. Si bien el uso de una dirección que se desvía de la dirección de descenso más empinada puede parecer contrario a la intuición, la idea es que la pendiente más pequeña se puede compensar manteniéndose en una distancia mucho más larga. ${\ Displaystyle \ gamma}$${\ Displaystyle \ gamma}$${\ Displaystyle \ gamma}$

Para razonar sobre esto matemáticamente, usemos una dirección y un tamaño de paso y consideremos la actualización más general: ${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$

${\ Displaystyle \ mathbf {a} _ {n + 1} = \ mathbf {a} _ {n} - \ gamma _ {n} \, \ mathbf {p} _ {n}}$.

Encontrar una buena configuración de y requiere un poco de reflexión. En primer lugar, nos gustaría que la dirección de actualización apunte cuesta abajo. Matemáticamente, dejar denotar el ángulo entre y , esto requiere que Para decir más, necesitamos más información sobre la función objetivo que estamos optimizando. Bajo el supuesto bastante débil que es continuamente diferenciable, podemos probar que: ${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$${\ Displaystyle \ theta _ {n}}$${\ Displaystyle \ nabla F (\ mathbf {a_ {n}})}$${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ cos \ theta _ {n}> 0.}$${\ Displaystyle F}$

${\ Displaystyle F (\ mathbf {a} _ {n + 1}) \ leq F (\ mathbf {a} _ {n}) - \ gamma _ {n} \ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2} \ | \ mathbf {p} _ {n} \ | _ {2} \ left [\ cos \ theta _ {n} - \ max _ {t \ in [0,1 ]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} \ right]}$

( 1 )

Esta desigualdad implica que la cantidad en la que podemos estar seguros de que la función disminuye depende de una compensación entre los dos términos entre corchetes. El primer término entre corchetes mide el ángulo entre la dirección de descenso y la pendiente negativa. El segundo término mide la rapidez con que cambia el gradiente a lo largo de la dirección de descenso. ${\ Displaystyle F}$

En principio, la desigualdad ( 1 ) podría optimizarse y elegir un tamaño y una dirección de paso óptimos. El problema es que evaluar el segundo término entre corchetes requiere una evaluación , y las evaluaciones de gradiente adicionales son generalmente costosas e indeseables. Algunas formas de solucionar este problema son: ${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$${\ Displaystyle \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})}$

• Olvídese de los beneficios de una dirección de descenso inteligente estableciendo y use la búsqueda de línea para encontrar un tamaño de paso adecuado , como uno que satisfaga las condiciones de Wolfe .${\ Displaystyle \ mathbf {p} _ {n} = \ nabla F (\ mathbf {a_ {n}})}$${\ Displaystyle \ gamma _ {n}}$
• Suponiendo que sea ​​dos veces diferenciable, use su hessiano para estimar Luego elija y optimizando la desigualdad ( 1 ).${\ Displaystyle F}$${\ Displaystyle \ nabla ^ {2} F}$${\ Displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ approx \ | t \ gamma _ {n} \ nabla ^ {2} F (\ mathbf {a} _ {n}) \ mathbf {p} _ {n} \ |.}$${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$
• Suponiendo que es Lipschitz , use su constante de Lipschitz para enlazar Luego elija y optimizando la desigualdad ( 1 ).${\ Displaystyle \ nabla F}$${\ Displaystyle L}$${\ Displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ leq Lt \ gamma _ {n} \ | \ mathbf {p} _ {n} \ |.}$${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$
• Cree un modelo personalizado de for . Luego elija y optimizando la desigualdad ( 1 ).${\ Displaystyle \ max _ {t \ in [0,1]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ { n}) - \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} }$${\ Displaystyle F}$${\ Displaystyle \ mathbf {p} _ {n}}$${\ Displaystyle \ gamma _ {n}}$
• Bajo supuestos más sólidos sobre la función , como la convexidad , pueden ser posibles técnicas más avanzadas .${\ Displaystyle F}$

Por lo general, siguiendo una de las recetas anteriores, se puede garantizar la convergencia a un mínimo local. Cuando la función es convexa , todos los mínimos locales también son mínimos globales, por lo que en este caso el descenso del gradiente puede converger a la solución global. ${\ Displaystyle F}$

Solución de un sistema lineal

El algoritmo de descenso más pronunciado aplicado al filtro Wiener

El descenso de gradiente se puede utilizar para resolver un sistema de ecuaciones lineales

${\ Displaystyle A \ mathbf {x} - \ mathbf {b} = 0}$

reformulado como un problema de minimización cuadrática. Si la matriz del sistema es simétrica real y definida positiva , una función objetivo se define como la función cuadrática, con la minimización de ${\ Displaystyle A}$

${\ Displaystyle F (\ mathbf {x}) = \ mathbf {x} ^ {T} A \ mathbf {x} -2 \ mathbf {x} ^ {T} \ mathbf {b},}$

así que eso

${\ Displaystyle \ nabla F (\ mathbf {x}) = 2 (A \ mathbf {x} - \ mathbf {b}).}$

Para una matriz real general , los mínimos cuadrados lineales definen ${\ Displaystyle A}$

${\ Displaystyle F (\ mathbf {x}) = \ left \ | A \ mathbf {x} - \ mathbf {b} \ right \ | ^ {2}.}$

En lineales de mínimos cuadrados tradicionales de los bienes y la norma euclidiana se utiliza, en cuyo caso ${\ Displaystyle A}$${\ Displaystyle \ mathbf {b}}$

${\ Displaystyle \ nabla F (\ mathbf {x}) = 2A ^ {T} (A \ mathbf {x} - \ mathbf {b}).}$

La minimización de la búsqueda de líneas , encontrando el tamaño de paso localmente óptimo en cada iteración, se puede realizar analíticamente para funciones cuadráticas, y se conocen fórmulas explícitas para el localmente óptimo . ${\ Displaystyle \ gamma}$${\ Displaystyle \ gamma}$

Por ejemplo, para una matriz real simétrica y definida positiva , un algoritmo simple puede ser el siguiente: ${\ Displaystyle A}$

${\ displaystyle {\ begin {alineado} & {\ text {repetir en el bucle:}} \\ & \ qquad \ mathbf {r}: = \ mathbf {b} - \ mathbf {Ax} \\ & \ qquad \ gamma: = {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r}} / {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf {x}: = \ mathbf {x} + \ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r} { \ text {es lo suficientemente pequeño, luego sale del ciclo}} \\ & {\ text {finaliza el ciclo de repetición}} \\ & {\ text {return}} \ mathbf {x} {\ text {como resultado}} \ end {alineado}}}$

Para evitar multiplicar por dos veces por iteración, observamos que implica , lo que da el algoritmo tradicional, ${\ Displaystyle A}$${\ Displaystyle \ mathbf {x}: = \ mathbf {x} + \ gamma \ mathbf {r}}$${\ Displaystyle \ mathbf {r}: = \ mathbf {r} - \ gamma \ mathbf {Ar}}$

${\ displaystyle {\ begin {alineado} & \ mathbf {r}: = \ mathbf {b} - \ mathbf {Ax} \\ & {\ text {repetir en el bucle:}} \\ & \ qquad \ gamma: = {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r}} / {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf { x}: = \ mathbf {x} + \ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r} {\ text {es lo suficientemente pequeño, luego sale del ciclo}} \\ & \ qquad \ mathbf {r}: = \ mathbf {r} - \ gamma \ mathbf {Ar} \\ & {\ text {fin del ciclo de repetición}} \\ & {\ text {return}} \ mathbf {x} {\ text {como resultado}} \ end {alineado}}}$

El método rara vez se usa para resolver ecuaciones lineales, siendo el método de gradiente conjugado una de las alternativas más populares. El número de iteraciones de descenso de gradiente es comúnmente proporcional al número de condición espectral de la matriz del sistema (la relación entre los valores propios máximo y mínimo de ) , mientras que la convergencia del método de gradiente conjugado generalmente se determina mediante una raíz cuadrada del número de condición, es decir , es mucho más rápido. Ambos métodos pueden beneficiarse del preacondicionamiento , donde el descenso del gradiente puede requerir menos suposiciones en el preacondicionador. ${\ Displaystyle \ kappa (A)}$${\ Displaystyle A}$${\ Displaystyle A ^ {T} A}$

Solución de un sistema no lineal

El descenso de gradiente también se puede utilizar para resolver un sistema de ecuaciones no lineales . A continuación se muestra un ejemplo que muestra cómo usar el descenso de gradiente para resolver tres variables desconocidas, x ₁ , x ₂ y x ₃ . Este ejemplo muestra una iteración del descenso de gradiente.

Considere el sistema de ecuaciones no lineal

${\ Displaystyle {\ begin {cases} 3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ tfrac {3} {2}} = 0 \\ 4x_ {1} ^ {2} - 625x_ {2} ^ {2} + 2x_ {2} -1 = 0 \\\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ tfrac {10 \ pi -3} {3 }} = 0 \ end {cases}}}$

Introducimos la función asociada

${\ Displaystyle G (\ mathbf {x}) = {\ begin {bmatrix} 3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ tfrac {3} {2}} \\ 4x_ { 1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 \\\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ tfrac {10 \ pi -3} {3}} \\\ end {bmatrix}},}$

dónde

${\ Displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \\\ end {bmatrix}}.}$

Ahora se podría definir la función objetivo

${\ Displaystyle F (\ mathbf {x}) = {\ frac {1} {2}} G ^ {\ mathrm {T}} (\ mathbf {x}) G (\ mathbf {x}) = {\ frac {1} {2}} \ left [\ left (3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ frac {3} {2}} \ right) ^ {2} + \ izquierda (4x_ {1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 \ derecha) ^ {2} + \ izquierda (\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ frac {10 \ pi -3} {3}} \ right) ^ {2} \ right],}$

que intentaremos minimizar. Como conjetura inicial, usemos

${\ displaystyle \ mathbf {x} ^ {(0)} = \ mathbf {0} = {\ begin {bmatrix} 0 \\ 0 \\ 0 \\\ end {bmatrix}}.}$

Lo sabemos

${\ Displaystyle \ mathbf {x} ^ {(1)} = \ mathbf {0} - \ gamma _ {0} \ nabla F (\ mathbf {0}) = \ mathbf {0} - \ gamma _ {0} J_ {G} (\ mathbf {0}) ^ {\ mathrm {T}} G ​​(\ mathbf {0}),}$

donde la matriz jacobiana está dada por ${\ Displaystyle J_ {G}}$

${\ displaystyle J_ {G} (\ mathbf {x}) = {\ begin {bmatrix} 3 & \ sin (x_ {2} x_ {3}) x_ {3} & \ sin (x_ {2} x_ {3} ) x_ {2} \\ 8x_ {1} y - 1250x_ {2} + 2 y 0 \\ - x_ {2} \ exp {(-x_ {1} x_ {2})} y - x_ {1} \ exp ( -x_ {1} x_ {2}) y 20 \\\ end {bmatrix}}.}$

Calculamos:

${\ displaystyle J_ {G} (\ mathbf {0}) = {\ begin {bmatrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 20 \ end {bmatrix}}, \ qquad G (\ mathbf {0}) = {\ begin { bmatrix} -2.5 \\ - 1 \\ 10.472 \ end {bmatrix}}.}$

Por lo tanto

${\ displaystyle \ mathbf {x} ^ {(1)} = \ mathbf {0} - \ gamma _ {0} {\ begin {bmatrix} -7.5 \\ - 2 \\ 209.44 \ end {bmatrix}},}$

y

${\ displaystyle F (\ mathbf {0}) = 0.5 \ left ((- 2.5) ^ {2} + (- 1) ^ {2} + (10.472) ^ {2} \ right) = 58.456.}$

Una animación que muestra las primeras 83 iteraciones de descenso de gradiente aplicadas a este ejemplo. Las superficies son isosuperficies de la estimación actual y las flechas muestran la dirección de descenso. Debido a un tamaño de paso pequeño y constante, la convergencia es lenta.${\ Displaystyle F (\ mathbf {x} ^ {(n)})}$${\ Displaystyle \ mathbf {x} ^ {(n)}}$

Ahora, se debe encontrar un adecuado tal que ${\ Displaystyle \ gamma _ {0}}$

${\ Displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) \ leq F \ left (\ mathbf {x} ^ {(0)} \ right) = F (\ mathbf {0}) .}$

Esto se puede hacer con cualquiera de una variedad de algoritmos de búsqueda de líneas . También se podría simplemente adivinar cuál da ${\ Displaystyle \ gamma _ {0} = 0.001,}$

${\ displaystyle \ mathbf {x} ^ {(1)} = {\ begin {bmatrix} 0,0075 \\ 0,002 \\ - 0,20944 \\\ end {bmatrix}}.}$

Al evaluar la función objetivo en este valor, se obtiene

${\ displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) = 0.5 \ left ((- 2.48) ^ {2} + (- 1.00) ^ {2} + (6.28) ^ {2 } \ right) = 23.306.}$

La disminución desde el valor del siguiente paso de ${\ Displaystyle F (\ mathbf {0}) = 58,456}$

${\ Displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) = 23,306}$

es una disminución considerable de la función objetivo. Más pasos reducirían su valor aún más, hasta que se encontrara una solución aproximada al sistema.

Comentarios

El descenso de gradiente funciona en espacios de cualquier número de dimensiones, incluso en dimensiones infinitas. En el último caso, el espacio de búsqueda es típicamente un espacio de función , y se calcula la derivada de Fréchet del funcional que se minimizará para determinar la dirección de descenso.

Ese descenso de gradiente funciona en cualquier número de dimensiones (número finito al menos) puede verse como una consecuencia de la desigualdad de Cauchy-Schwarz . Ese artículo prueba que la magnitud del producto interno (punto) de dos vectores de cualquier dimensión se maximiza cuando son colineales. En el caso del descenso de gradiente, sería cuando el vector de ajustes de variables independientes es proporcional al vector de gradiente de derivadas parciales.

El descenso del gradiente puede tomar muchas iteraciones para calcular un mínimo local con la precisión requerida , si la curvatura en diferentes direcciones es muy diferente para la función dada. Para tales funciones, el preacondicionamiento , que cambia la geometría del espacio para dar forma a los conjuntos de niveles de función como círculos concéntricos , cura la convergencia lenta. Sin embargo, construir y aplicar el preacondicionamiento puede resultar computacionalmente costoso.

El descenso de gradiente se puede combinar con una búsqueda de líneas , encontrando el tamaño de paso óptimo localmente en cada iteración. Realizar la búsqueda de línea puede llevar mucho tiempo. Por el contrario, el uso de un valor pequeño fijo puede producir una convergencia deficiente. ${\ Displaystyle \ gamma}$${\ Displaystyle \ gamma}$

Los métodos basados ​​en el método de Newton y la inversión del hessiano utilizando técnicas de gradiente conjugado pueden ser mejores alternativas. Generalmente, estos métodos convergen en menos iteraciones, pero el costo de cada iteración es mayor. Un ejemplo es el método BFGS que consiste en calcular en cada paso una matriz por la cual se multiplica el vector de gradiente para ir en una dirección "mejor", combinado con un algoritmo de búsqueda de líneas más sofisticado , para encontrar el "mejor" valor de Para extremadamente problemas grandes, donde dominan los problemas de memoria de la computadora, se debe usar un método de memoria limitada como L-BFGS en lugar de BFGS o el descenso más pronunciado. ${\ Displaystyle \ gamma.}$

El descenso de gradiente puede verse como la aplicación del método de Euler para resolver ecuaciones diferenciales ordinarias a un flujo de gradiente . A su vez, esta ecuación se puede derivar como un controlador óptimo para el sistema de control con dado en forma de la regeneración . ${\ Displaystyle x '(t) = - \ nabla f (x (t))}$${\ Displaystyle x '(t) = u (t)}$${\ Displaystyle u (t)}$${\ Displaystyle u (t) = - \ nabla f (x (t))}$

Modificaciones

El descenso en gradiente puede converger a un mínimo local y disminuir la velocidad en un vecindario de un punto de silla . Incluso para la minimización cuadrática sin restricciones, el descenso de gradiente desarrolla un patrón en zig-zag de iteraciones posteriores a medida que avanzan las iteraciones, lo que resulta en una convergencia lenta. Se han propuesto múltiples modificaciones del descenso de gradientes para abordar estas deficiencias.

Métodos de gradiente rápido

Yurii Nesterov ha propuesto una modificación simple que permite una convergencia más rápida para problemas convexos y desde entonces se ha generalizado aún más. Para problemas suaves sin restricciones, el método se denomina método de gradiente rápido (FGM) o método de gradiente acelerado (AGM). Específicamente, si la función diferenciable es convexa y es Lipschitz , y no se supone que sea fuertemente convexa , entonces el error en el valor objetivo generado en cada paso por el método de descenso de gradiente estará acotado por . Usando la técnica de aceleración de Nesterov, el error disminuye en . Se sabe que la tasa de disminución de la función de costo es óptima para los métodos de optimización de primer orden. Sin embargo, existe la oportunidad de mejorar el algoritmo reduciendo el factor constante. El método de gradiente optimizado (OGM) reduce esa constante en un factor de dos y es un método óptimo de primer orden para problemas a gran escala. ${\ Displaystyle F}$${\ Displaystyle \ nabla F}$${\ Displaystyle F}$${\ Displaystyle k}$ ${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k}} \ right)}$${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k ^ {2}}} \ right)}$${\ Displaystyle {\ mathcal {O}} \ left ({k ^ {- 2}} \ right)}$

Para problemas restringidos o no suaves, la MGF de Nesterov se denomina método de gradiente proximal rápido (FPGM), una aceleración del método de gradiente proximal .

Momento o método de bola pesada

Al tratar de romper el patrón en zig-zag del descenso de gradiente, el método de la bola pesada o impulso utiliza un término de impulso en analogía a una bola pesada que se desliza sobre la superficie de valores de la función que se minimiza, o al movimiento de masas en la dinámica newtoniana a través de un viscoso medio en un campo de fuerza conservador. El descenso de gradiente con impulso recuerda la actualización de la solución en cada iteración y determina la siguiente actualización como una combinación lineal del gradiente y la actualización anterior. Para la minimización cuadrática sin restricciones, un límite de velocidad de convergencia teórica del método de bola pesada es asintóticamente igual que el del método de gradiente conjugado óptimo .

Esta técnica se utiliza en el descenso de gradiente estocástico # Momentum y como una extensión de los algoritmos de retropropagación utilizados para entrenar redes neuronales artificiales .

Extensiones

El descenso de gradiente se puede extender para manejar restricciones al incluir una proyección en el conjunto de restricciones. Este método solo es factible cuando la proyección se puede calcular de manera eficiente en una computadora. Bajo supuestos adecuados, este método converge. Este método es un caso específico del algoritmo hacia adelante y hacia atrás para inclusiones monótonas (que incluye programación convexa y desigualdades variacionales ).

Ver también

Referencias

Otras lecturas

• Boyd, Stephen ; Vandenberghe, Lieven (2004). "Minimización sin restricciones" (PDF) . Optimización convexa . Nueva York: Cambridge University Press. págs. 457–520. ISBN 0-521-83378-7.
• Chong, Edwin KP; Żak, Stanislaw H. (2013). "Métodos de gradiente" . Introducción a la optimización (cuarta edición). Hoboken: Wiley. págs. 131–160. ISBN 978-1-118-27901-4.
• Himmelblau, David M. (1972). "Procedimientos de minimización sin restricciones mediante derivados". Programación no lineal aplicada . Nueva York: McGraw-Hill. págs. 63-132. ISBN 0-07-028921-2.

enlaces externos

• Usando el descenso de gradiente en C ++, Boost, Ublas para regresión lineal
• Una serie de videos de Khan Academy discute el ascenso en gradiente
• Libro en línea que enseña el descenso de gradientes en el contexto de una red neuronal profunda
• "Gradient Descent, cómo aprenden las redes neuronales" . 3Azul1Marrón . 16 de octubre de 2017 - a través de YouTube .

arxiv.org/2108.1283