Fundamentos de la geometría - Foundations of geometry

Los fundamentos de la geometría son el estudio de las geometrías como sistemas axiomáticos . Hay varios conjuntos de axiomas que dan lugar a geometrías euclidianas o no euclidianas . Estos son fundamentales para el estudio y de importancia histórica, pero hay una gran cantidad de geometrías modernas que no son euclidianas que pueden estudiarse desde este punto de vista. El término geometría axiomática se puede aplicar a cualquier geometría que se desarrolle a partir de un sistema de axiomas, pero a menudo se usa para referirse a la geometría euclidiana estudiada desde este punto de vista. La integridad y la independencia de los sistemas axiomáticos generales son consideraciones matemáticas importantes, pero también hay cuestiones relacionadas con la enseñanza de la geometría que entran en juego.

Sistemas axiomáticos

Basado en métodos griegos antiguos, un sistema axiomático es una descripción formal de una forma de establecer la verdad matemática que fluye de un conjunto fijo de supuestos. Aunque es aplicable a cualquier área de las matemáticas, la geometría es la rama de las matemáticas elementales en la que este método se ha aplicado con mayor éxito.

Hay varios componentes de un sistema axiomático.

1. Los primitivos (términos indefinidos) son las ideas más básicas. Por lo general, incluyen objetos y relaciones. En geometría, los objetos son cosas como puntos , líneas y planos, mientras que una relación fundamental es la de incidencia , de un objeto que se encuentra o se une a otro. Los términos en sí mismos no están definidos. Hilbert comentó una vez que en lugar de puntos, líneas y planos, también se podría hablar de mesas, sillas y jarras de cerveza. Su punto es que los términos primitivos son simplemente cáscaras vacías, marcadores de posición si se quiere, y no tienen propiedades intrínsecas.
2. Los axiomas (o postulados) son declaraciones sobre estos primitivos; por ejemplo, dos puntos cualesquiera inciden juntos con una sola línea (es decir, que para dos puntos cualesquiera, solo hay una línea que pasa por ambos). Se asume que los axiomas son verdaderos y no se prueban. Son los componentes básicos de los conceptos geométricos, ya que especifican las propiedades que tienen las primitivas.
3. Las leyes de la lógica .
4. Los teoremas son las consecuencias lógicas de los axiomas, es decir, los enunciados que se pueden obtener de los axiomas utilizando las leyes de la lógica deductiva.

Una interpretación de un sistema axiomático es una forma particular de dar un significado concreto a los primitivos de ese sistema. Si esta asociación de significados hace que los axiomas del sistema sean enunciados verdaderos, entonces la interpretación se denomina modelo del sistema. En un modelo, todos los teoremas del sistema son automáticamente enunciados verdaderos.

Propiedades de los sistemas axiomáticos

Al discutir los sistemas axiomáticos, a menudo se enfocan varias propiedades en:

• Se dice que los axiomas de un sistema axiomático son consistentes si no se puede derivar de ellos ninguna contradicción lógica. Excepto en los sistemas más simples, la consistencia es una propiedad difícil de establecer en un sistema axiomático. Por otro lado, si existe un modelo para el sistema axiomático, entonces cualquier contradicción derivable en el sistema también es derivable en el modelo, y el sistema axiomático es tan consistente como cualquier sistema al que pertenezca el modelo. Esta propiedad (tener un modelo) se conoce como consistencia relativa o consistencia del modelo .
• Un axioma se llama independiente si no se puede probar o refutar a partir de los otros axiomas del sistema axiomático. Se dice que un sistema axiomático es independiente si cada uno de sus axiomas es independiente. Si un enunciado verdadero es una consecuencia lógica de un sistema axiomático, entonces será un enunciado verdadero en todos los modelos de ese sistema. Para probar que un axioma es independiente de los axiomas restantes del sistema, es suficiente encontrar dos modelos de los axiomas restantes, para los cuales el axioma es un enunciado verdadero en uno y un enunciado falso en el otro. La independencia no siempre es una propiedad deseable desde un punto de vista pedagógico.
• Un sistema axiomático se llama completo si cada enunciado expresable en los términos del sistema es demostrable o tiene una negación demostrable. Otra forma de afirmar esto es que no se puede agregar ningún enunciado independiente a un sistema axiomático completo que sea consistente con los axiomas de ese sistema.
• Un sistema axiomático es categórico si dos modelos cualesquiera del sistema son isomórficos (esencialmente, solo hay un modelo para el sistema). Un sistema categórico es necesariamente completo, pero la integridad no implica categoricidad. En algunas situaciones, la categoricidad no es una propiedad deseable, ya que los sistemas axiomáticos categóricos no pueden generalizarse. Por ejemplo, el valor del sistema axiomático para la teoría de grupos es que no es categórico, por lo que demostrar un resultado en la teoría de grupos significa que el resultado es válido en todos los diferentes modelos para la teoría de grupos y uno no tiene que reprobar el resultado. en cada uno de los modelos no isomorfos.

Geometría euclidiana

La geometría euclidiana es un sistema matemático atribuido al matemático griego alejandrino Euclides , que describió (aunque no rigurosamente según los estándares modernos) en su libro de texto sobre geometría : los elementos . El método de Euclides consiste en asumir un pequeño conjunto de axiomas intuitivamente atractivos y deducir muchas otras proposiciones ( teoremas ) de estos. Aunque muchos de los resultados de Euclides habían sido establecidos por matemáticos anteriores, Euclides fue el primero en mostrar cómo estas proposiciones podían encajar en un sistema lógico y deductivo comprensivo . Los Elementos comienzan con la geometría plana, que todavía se enseña en la escuela secundaria como el primer sistema axiomático y los primeros ejemplos de demostración formal . Continúa con la geometría sólida de tres dimensiones . Gran parte de los Elementos establece los resultados de lo que ahora se llama álgebra y teoría de números , explicados en lenguaje geométrico.

Durante más de dos mil años, el adjetivo "euclidiano" fue innecesario porque no se había concebido ningún otro tipo de geometría. Los axiomas de Euclides parecían tan intuitivamente obvios (con la posible excepción del postulado paralelo ) que cualquier teorema probado a partir de ellos se consideraba verdadero en un sentido absoluto, a menudo metafísico. En la actualidad, sin embargo, se conocen muchas otras geometrías que no son euclidianas, y las primeras se descubrieron a principios del siglo XIX.

Elementos de Euclides

Elementos de Euclides es un tratado matemático y geométrico que consta de 13 libros escritos por el antiguo matemático griego Euclides en Alejandría c. 300 AC. Es una colección de definiciones, postulados ( axiomas ), proposiciones ( teoremas y construcciones ) y pruebas matemáticas de las proposiciones. Los trece libros cubren la geometría euclidiana y la versión griega antigua de la teoría de números elemental . Con la excepción de Sobre la esfera móvil de Autolycus , los Elementos es uno de los tratados matemáticos griegos más antiguos que existen, y es el tratamiento deductivo axiomático más antiguo que existe de las matemáticas . Ha demostrado ser fundamental en el desarrollo de la lógica y la ciencia moderna .

Euclid's Elements ha sido referido como el libro de texto más exitoso e influyente jamás escrito. Habiendo sido escrito por primera vez en Venecia en 1482, es una de las primeras obras matemáticas que se imprimieron después de la invención de la imprenta y fue estimado por Carl Benjamin Boyer como el segundo después de la Biblia en el número de ediciones publicadas. con el número llegando a más de mil. Durante siglos, cuando el quadrivium se incluyó en el plan de estudios de todos los estudiantes universitarios, se exigió a todos los estudiantes el conocimiento de al menos parte de los Elementos de Euclides . No fue sino hasta el siglo XX, cuando su contenido se enseñó universalmente a través de otros libros de texto escolares, que dejó de ser considerado algo que todas las personas educadas habían leído.

Los Elementos son principalmente una sistematización de conocimientos previos de geometría. Se supone que se reconoció su superioridad sobre los tratamientos anteriores, con la consecuencia de que hubo poco interés en preservar los anteriores, y ahora están casi todos perdidos.

Los libros I – IV y VI discuten la geometría plana. Se prueban muchos resultados sobre figuras planas, por ejemplo, si un triángulo tiene dos ángulos iguales, entonces los lados subtendidos por los ángulos son iguales. Se demuestra el teorema de Pitágoras .

Los libros V y VII-X tratan de la teoría de números, con números tratados geométricamente a través de su representación como segmentos de línea con varias longitudes. Se introducen nociones como números primos y números racionales e irracionales . Se demuestra la infinitud de los números primos.

Los libros XI-XIII se refieren a la geometría sólida. Un resultado típico es la relación 1: 3 entre el volumen de un cono y un cilindro con la misma altura y base.

El postulado paralelo: si dos líneas se cruzan con una tercera de tal manera que la suma de los ángulos internos de un lado es menor que dos ángulos rectos, entonces las dos líneas inevitablemente deben cruzarse entre sí en ese lado si se extienden lo suficiente.

Cerca del comienzo del primer libro de los Elementos , Euclides da cinco postulados (axiomas) para la geometría plana, expresados ​​en términos de construcciones (traducidos por Thomas Heath):

"Postulemos lo siguiente":

1. "Dibujar una línea recta desde cualquier punto a cualquier punto".
2. "Para producir [extender] una línea recta finita continuamente en línea recta".
3. "Para describir un círculo con cualquier centro y distancia [radio]".
4. "Que todos los ángulos rectos son iguales entre sí".
5. El postulado paralelo : "Que, si una línea recta que cae sobre dos líneas rectas hace que los ángulos interiores del mismo lado sean menores que dos ángulos rectos, las dos líneas rectas, si se producen indefinidamente, se encuentran en el lado en el que están los ángulos menores que los dos ángulos rectos ".

Aunque la declaración de Euclides de los postulados solo afirma explícitamente la existencia de las construcciones, también se supone que producen objetos únicos.

El éxito de los Elementos se debe principalmente a su presentación lógica de la mayor parte del conocimiento matemático disponible para Euclides. Gran parte del material no es original de él, aunque muchas de las pruebas son supuestamente suyas. El desarrollo sistemático de Euclides de su tema, desde un pequeño conjunto de axiomas hasta resultados profundos, y la coherencia de su enfoque a lo largo de los Elementos , alentó su uso como libro de texto durante unos 2000 años. The Elements todavía influye en los libros de geometría moderna. Además, su enfoque axiomático lógico y sus pruebas rigurosas siguen siendo la piedra angular de las matemáticas.

Una crítica de Euclides

Los estándares de rigor matemático han cambiado desde que Euclides escribió los Elementos . Las actitudes y los puntos de vista modernos hacia un sistema axiomático pueden hacer parecer que Euclides fue de alguna manera descuidado o descuidado en su enfoque del tema, pero esto es una ilusión ahistórica. Es solo después de que los cimientos fueron examinados cuidadosamente en respuesta a la introducción de la geometría no euclidiana que comenzaron a surgir lo que ahora consideramos fallas . El matemático e historiador WW Rouse Ball puso estas críticas en perspectiva y señaló que "el hecho de que durante dos mil años [los Elementos ] fuera el libro de texto habitual sobre el tema plantea una fuerte presunción de que no es inadecuado para ese propósito".

Algunos de los principales problemas con la presentación de Euclid son:

• Falta de reconocimiento del concepto de términos primitivos , objetos y nociones que deben dejarse sin definir en el desarrollo de un sistema axiomático.
• El uso de la superposición en algunas pruebas sin que exista una justificación axiomática de este método.
• Falta de un concepto de continuidad, que es necesario para probar la existencia de algunos puntos y líneas que construye Euclides.
• Falta de claridad sobre si una línea recta es infinita o sin límites en el segundo postulado.
• Falta del concepto de intermediación utilizado, entre otras cosas, para distinguir entre el interior y el exterior de varias figuras.

La lista de axiomas de Euclides en los Elementos no era exhaustiva, pero representaba los principios que parecían más importantes. Sus pruebas a menudo invocan nociones axiomáticas que no se presentaron originalmente en su lista de axiomas. No se extravía y prueba cosas erróneas por ello, ya que hace uso de supuestos implícitos cuya validez parece estar justificada por los diagramas que acompañan a sus demostraciones. Los matemáticos posteriores han incorporado los supuestos axiomáticos implícitos de Euclides en la lista de axiomas formales, ampliando así enormemente esa lista.

Por ejemplo, en la primera construcción del Libro 1, Euclides usó una premisa que no fue postulada ni probada: que dos círculos con centros a la distancia de su radio se intersecarán en dos puntos. Más tarde, en la cuarta construcción, usó la superposición (moviendo los triángulos uno encima del otro) para demostrar que si dos lados y sus ángulos son iguales, entonces son congruentes; durante estas consideraciones utiliza algunas propiedades de superposición, pero estas propiedades no se describen explícitamente en el tratado. Si la superposición se considera un método válido de demostración geométrica, toda la geometría estaría llena de tales demostraciones. Por ejemplo, las proposiciones I.1 a I.3 pueden probarse trivialmente usando superposición.

Para abordar estos problemas en el trabajo de Euclides, los autores posteriores han intentado llenar los huecos en la presentación de Euclides (el más notable de estos intentos se debe a D. Hilbert ) o organizar el sistema de axiomas en torno a diferentes conceptos, como lo ha hecho GD Birkhoff. .

Pasch y Peano

El matemático alemán Moritz Pasch (1843-1930) fue el primero en realizar la tarea de colocar la geometría euclidiana sobre una base axiomática firme. En su libro, Vorlesungen über neuere Geometrie, publicado en 1882, Pasch sentó las bases del método axiomático moderno. Él originó el concepto de noción primitiva (que llamó Kernbegriffe ) y junto con los axiomas ( Kernsätzen ) construye un sistema formal que está libre de cualquier influencia intuitiva. Según Pasch, el único lugar donde la intuición debería desempeñar un papel es decidir cuáles deberían ser las nociones y axiomas primitivos. Por lo tanto, para Pasch, el punto es una noción primitiva, pero la línea (línea recta) no lo es, ya que tenemos una buena intuición sobre los puntos, pero nadie ha visto o tenido experiencia con una línea infinita. La noción primitiva que Pasch usa en su lugar es segmento de línea .

Pasch observó que el orden de los puntos en una línea (o, de manera equivalente, las propiedades de contención de los segmentos de línea) no se resuelve adecuadamente mediante los axiomas de Euclides; por lo tanto, el teorema de Pasch , que establece que si se cumplen dos relaciones de contención de segmento de línea, entonces también se cumple una tercera, no puede probarse a partir de los axiomas de Euclides. El axioma de Pasch relacionado se refiere a las propiedades de intersección de líneas y triángulos.

El trabajo de Pasch sobre los cimientos estableció el estándar de rigor, no solo en geometría sino también en el contexto más amplio de las matemáticas. Sus ideas revolucionarias son ahora tan comunes que es difícil recordar que tuvieron un único creador. El trabajo de Pasch influyó directamente en muchos otros matemáticos, en particular D. Hilbert y el matemático italiano Giuseppe Peano (1858-1932). El trabajo de 1889 de Peano sobre geometría, en gran parte una traducción del tratado de Pasch a la notación de la lógica simbólica (que Peano inventó), utiliza las nociones primitivas de punto e intermediación . Peano rompe el lazo empírico en la elección de nociones y axiomas primitivos que Pasch requería. Para Peano, todo el sistema es puramente formal, divorciado de cualquier información empírica.

Pieri y la escuela italiana de geómetras

El matemático italiano Mario Pieri (1860-1913) adoptó un enfoque diferente y consideró un sistema en el que solo había dos nociones primitivas, la de punto y la de movimiento . Pasch había usado cuatro primitivos y Peano lo había reducido a tres, pero ambos enfoques se basaban en algún concepto de intermediación que Pieri reemplazó por su formulación del movimiento . En 1905, Pieri dio el primer tratamiento axiomático de la geometría proyectiva compleja que no comenzó construyendo geometría proyectiva real .

Pieri era miembro de un grupo de geómetras y lógicos italianos que Peano había reunido a su alrededor en Turín. Este grupo de asistentes, colegas jóvenes y otros se dedicó a llevar a cabo el programa lógico-geométrico de Peano de poner los cimientos de la geometría en una base axiomática firme basada en el simbolismo lógico de Peano. Además de Pieri, Burali-Forti , Padoa y Fano estaban en este grupo. En 1900 hubo dos conferencias internacionales consecutivas en París, el Congreso Internacional de Filosofía y el Segundo Congreso Internacional de Matemáticos . Este grupo de matemáticos italianos estuvo muy presente en estos congresos, impulsando su agenda axiomática. Padoa dio una charla bien considerada y Peano, en el período de preguntas después del famoso discurso de David Hilbert sobre problemas no resueltos , comentó que sus colegas ya habían resuelto el segundo problema de Hilbert.

Los axiomas de Hilbert

David Hilbert

En la Universidad de Gotinga, durante el período de invierno de 1898-1899, el eminente matemático alemán David Hilbert (1862-1943) presentó un curso de conferencias sobre los fundamentos de la geometría. A petición de Felix Klein , se le pidió al profesor Hilbert que redactara las notas de la conferencia para este curso a tiempo para la ceremonia de dedicación del verano de 1899 de un monumento a CF Gauss y Wilhelm Weber que se llevaría a cabo en la universidad. Las conferencias reorganizadas se publicaron en junio de 1899 con el título Grundlagen der Geometrie (Fundamentos de la geometría). La influencia del libro fue inmediata. Según Eves (1963 , págs. 384–5):

Al desarrollar un conjunto de postulados para la geometría euclidiana que no se aparta demasiado en espíritu del propio Euclides, y al emplear un mínimo de simbolismo, Hilbert logró convencer a los matemáticos en un grado mucho mayor que Pasch y Peano, de lo puramente hipotético-deductivo. naturaleza de la geometría. Pero la influencia del trabajo de Hilbert fue mucho más allá de esto, ya que, respaldado por la gran autoridad matemática del autor, implantó firmemente el método postulacional, no solo en el campo de la geometría, sino también esencialmente en todas las demás ramas de las matemáticas. El estímulo al desarrollo de los fundamentos de las matemáticas proporcionado por el librito de Hilbert es difícil de sobreestimar. Careciendo del extraño simbolismo de las obras de Pasch y Peano, la obra de Hilbert puede ser leída, en gran parte, por cualquier estudiante inteligente de geometría de secundaria.

Es difícil especificar los axiomas usados ​​por Hilbert sin referirse al historial de publicaciones de Grundlagen ya que Hilbert los cambió y modificó varias veces. La monografía original fue seguida rápidamente por una traducción al francés, en la que Hilbert agregó V.2, el axioma de integridad. EJ Townsend realizó una traducción al inglés, autorizada por Hilbert, que se registró con derechos de autor en 1902. Esta traducción incorporó los cambios realizados en la traducción al francés y, por lo tanto, se considera una traducción de la segunda edición. Hilbert continuó haciendo cambios en el texto y aparecieron varias ediciones en alemán. La séptima edición fue la última en aparecer en vida de Hilbert. Nuevas ediciones siguieron a la séptima, pero el texto principal esencialmente no fue revisado. Las modificaciones en estas ediciones ocurren en los apéndices y en los suplementos. Los cambios en el texto fueron grandes en comparación con el original y Open Court Publishers encargó una nueva traducción al inglés, que había publicado la traducción de Townsend. Entonces, la segunda edición en inglés fue traducida por Leo Unger de la décima edición en alemán en 1971. Esta traducción incorpora varias revisiones y ampliaciones de las ediciones alemanas posteriores de Paul Bernays. Las diferencias entre las dos traducciones al inglés se deben no solo a Hilbert, sino también a las diferentes elecciones de los dos traductores. Lo que sigue se basará en la traducción de Unger.

El sistema de axiomas de Hilbert se construye con seis nociones primitivas : punto , línea , plano , intermediación , mentiras sobre (contención) y congruencia .

Todos los puntos, líneas y planos de los siguientes axiomas son distintos a menos que se indique lo contrario.

I. Incidencia

1. Por cada dos puntos A y B existe una línea a que los contiene a ambos. Escribimos AB = a o BA = a . En lugar de "contiene", también podemos emplear otras formas de expresión; por ejemplo, podemos decir " A se encuentra sobre a ", " A es un punto de a ", " a pasa por A y por B ", " a une A con B ", etc. Si A se encuentra sobre a y en el mismo tiempo sobre otra línea b , que hacer uso también de la expresión: “las líneas una y b tienen el punto a en común”, etc.
2. Por cada dos puntos no existe más de una línea que los contenga a ambos; en consecuencia, si AB = a y AC = a , donde B ≠ C , entonces también BC = a .
3. Existen al menos dos puntos en una línea. Existen al menos tres puntos que no se encuentran en una línea.
4. Por cada tres puntos A , B , C no situados en la misma línea existe un plano α que los contiene a todos. Para cada plano existe un punto que se encuentra en él. Escribimos ABC = α . Empleamos también las expresiones: “ A , B , C , se encuentran en α”; “A, B, C son puntos de α”, etc.
5. Por cada tres puntos A , B , C que no se encuentran en la misma línea, no existe más de un plano que los contenga a todos.
6. Si dos puntos A , B de una línea a se encuentran en un plano α, entonces todos los puntos de a se encuentran en α. En este caso decimos: “La recta a está en el plano α”, etc.
7. Si dos planos α, β tienen un punto A en común, entonces tienen al menos un segundo punto B en común.
8. Existen al menos cuatro puntos que no se encuentran en un plano.

II. Pedido

1. Si un punto B se encuentra entre los puntos A y C , B también es de entre C y A , y no existe una línea que contiene los puntos distintos A, B, C .
2. Si A y C son dos puntos de una línea, entonces existe al menos un punto B que se extiende entre A y C .
3. De cualesquiera tres puntos situados en una línea, no hay más de uno que se encuentre entre los otros dos.
4. Axioma de Pascua : Let A , B , C tres puntos no puesto en la misma línea y dejar que un ser una línea situada en el plano ABC y no pasa a través de cualquiera de los puntos A , B , C . Entonces, si la línea a pasa por un punto del segmento AB , también pasará por un punto del segmento BC o por un punto del segmento AC .

III. Congruencia

1. Si A , B son dos puntos en una línea a , y si A ′ es un punto en la misma u otra línea a ′ , entonces, en un lado dado de A ′ en la línea recta a ′ , siempre podemos encontrar un punto B ′ de modo que el segmento AB sea ​​congruente con el segmento A′B ′ . Indicamos esta relación escribiendo AB ≅ A ′ B ′ . Cada segmento es congruente consigo mismo; es decir, siempre tenemos AB ≅ AB .
   Podemos enunciar el axioma anterior brevemente diciendo que cada segmento puede descartarse en un lado dado de un punto dado de una línea recta dada, al menos de una manera.
2. Si un segmento AB es congruente con el segmento A′B ′ y también con el segmento A ″ B ″ , entonces el segmento A′B ′ es congruente con el segmento A ″ B ″ ; es decir, si AB ≅ A′B ′ y AB ≅ A ″ B ″ , entonces A′B ′ ≅ A ″ B ″ .
3. Sean AB y BC dos segmentos de una recta a que no tienen puntos en común aparte del punto B y, además, sean A′B ′ y B′C ′ dos segmentos de la misma recta o de otra a ′ que tenga , asimismo, ningún otro punto que no sea B ′ en común. Entonces, si AB ≅ A′B ′ y BC ≅ B′C ′ , tenemos AC ≅ A′C ′ .
4. Sea un ángulo ∠ ( h , k ) en el plano α y una recta a ′ en un plano α ′. Supongamos también que, en el plano α ′, se asigna un lado definido de la línea recta a ′ . Denote por h ′ un rayo de la recta a ′ que emana de un punto O ′ de esta recta. Entonces en el plano α ′ hay uno y solo un rayo k ′ tal que el ángulo ∠ ( h , k ), o ∠ ( k , h ), es congruente con el ángulo ∠ ( h ′ , k ′ ) y en el Al mismo tiempo, todos los puntos interiores del ángulo ∠ ( h ′ , k ′ ) se encuentran en el lado dado de a ′ . Expresamos esta relación mediante la notación ∠ ( h , k ) ≅ ∠ ( h ′ , k ′ ).
5. Si el ángulo ∠ ( h , k ) es congruente con el ángulo ∠ ( h ′ , k ′ ) y con el ángulo ∠ ( h ″ , k ″ ), entonces el ángulo ∠ ( h ′ , k ′ ) es congruente con el ángulo ∠ ( h ″ , k ″ ); es decir, si ∠ ( h , k ) ≅ ∠ ( h ′ , k ′ ) y ∠ ( h , k ) ≅ ∠ ( h ″ , k ″ ), entonces ∠ ( h ′ , k ′ ) ≅ ∠ ( h ″ , k ″ ).

IV. Paralelas

1. (Axioma de Euclides): Sea a cualquier línea y A un punto que no está en ella. Entonces hay a lo sumo una línea en el plano, determinado por una y A , que pasa por A y no lo hace de intersección una .

V. Continuidad

1. Axioma de Arquímedes . Si AB y CD son cualquiera de los segmentos entonces existe un número n tal que n segmentos CD construida contigua desde A , a lo largo del rayo desde A a través de B , pasará más allá del punto B .
2. Axioma de completitud de la línea . Una extensión de un conjunto de puntos en una línea con su orden y relaciones de congruencia que preservaría las relaciones existentes entre los elementos originales, así como las propiedades fundamentales de orden de línea y congruencia que se siguen de los axiomas I-III y de V-1 es imposible.

Cambios en los axiomas de Hilbert

Cuando se tradujo al francés la monografía de 1899, Hilbert añadió:

V.2 Axioma de completitud . A un sistema de puntos, rectas y planos, es imposible agregar otros elementos de tal manera que el sistema así generalizado forme una nueva geometría que obedezca a los cinco grupos de axiomas. En otras palabras, los elementos de la geometría forman un sistema que no es susceptible de extensión, si consideramos válidos los cinco grupos de axiomas.

Este axioma no es necesario para el desarrollo de la geometría euclidiana, pero es necesario para establecer una biyección entre los números reales y los puntos de una línea. Este fue un ingrediente esencial en la prueba de Hilbert de la consistencia de su sistema de axiomas.

En la séptima edición del Grundlagen , este axioma había sido reemplazado por el axioma de completitud de la línea dado anteriormente y el antiguo axioma V.2 se convirtió en el Teorema 32.

También se puede encontrar en la monografía de 1899 (y que aparece en la traducción de Townsend):

II.4. Cualesquiera cuatro puntos A , B , C , D de una línea siempre se pueden etiquetar de modo que B se encuentre entre A y C y también entre A y D , y, además, que C esté entre A y D y también entre B y D .

Sin embargo, EH Moore y RL Moore demostraron de forma independiente que este axioma es redundante, y el primero publicó este resultado en un artículo que apareció en Transactions of the American Mathematical Society en 1902. Hilbert trasladó el axioma al Teorema 5 y volvió a numerar los axiomas en consecuencia (antiguo axioma II-5 (axioma de Pasch) ahora se convirtió en II-4).

Si bien no es tan dramático como estos cambios, la mayoría de los axiomas restantes también se modificaron en forma y / o función en el transcurso de las primeras siete ediciones.

Consistencia e independencia

Yendo más allá del establecimiento de un conjunto satisfactorio de axiomas, Hilbert también demostró la consistencia de su sistema en relación con la teoría de los números reales al construir un modelo de su sistema de axiomas a partir de los números reales. Demostró la independencia de algunos de sus axiomas construyendo modelos de geometrías que satisfacen todos excepto el axioma en consideración. Así, hay ejemplos de geometrías que satisfacen todos excepto el axioma de Arquímedes V.1 (geometrías no arquimedianas), todos excepto el axioma paralelo IV.1 (geometrías no euclidianas) y así sucesivamente. Utilizando la misma técnica, también mostró cómo algunos teoremas importantes dependían de ciertos axiomas y eran independientes de otros. Algunos de sus modelos eran muy complejos y otros matemáticos intentaron simplificarlos. Por ejemplo, el modelo de Hilbert para mostrar la independencia del teorema de Desargues de ciertos axiomas finalmente llevó a Ray Moulton a descubrir el plano de Moulton no desarguesiano . Estas investigaciones de Hilbert inauguraron virtualmente el estudio moderno de la geometría abstracta en el siglo XX.

Axiomas de Birkhoff

George David Birkhoff

En 1932, GD Birkhoff creó un conjunto de cuatro postulados de geometría euclidiana a los que a veces se hace referencia como axiomas de Birkhoff . Todos estos postulados se basan en la geometría básica que se puede verificar experimentalmente con una escala y un transportador . En una desviación radical del enfoque sintético de Hilbert, Birkhoff fue el primero en construir los cimientos de la geometría en el sistema de números reales . Es esta poderosa suposición la que permite el pequeño número de axiomas en este sistema.

Postulados

Birkhoff usa cuatro términos indefinidos: punto , línea , distancia y ángulo . Sus postulados son:

Postulado I: Postulado de la medida lineal . Los puntos A , B , ... de cualquier recta se pueden poner en correspondencia 1: 1 con los números reales x de modo que | x _B  - x _A | = D ( A, B ) para todos los puntos A y  B .  

Postulado II: Postulado punto-línea . Hay una y solo una línea recta, ℓ , que contiene dos puntos distintos P y  Q dados .

Postulado III: Postulado de la medida del ángulo . Los rayos { ℓ, m, n , ...} a través de cualquier punto O se pueden poner en correspondencia 1: 1 con los números reales a  (mod 2 π ) de modo que si A y B son puntos (no iguales a O ) de ℓ y m , respectivamente, la diferencia a _m  -  a _ℓ  (mod 2π) de los números asociados con las líneas ℓ y m es AOB . Además, si el punto B en m varía continuamente en una línea r que no contiene el vértice O , el número a _m varía continuamente también. ${\ Displaystyle \ angle}$

Postulado IV: Postulado de semejanza . Si en dos triángulos ABC y A'B'C '  y para alguna constante k  > 0, d ( A', B ' ) =  kd ( A, B ), d ( A', C '  ) =  kd ( A, C ) y B'A'C '   = ± BAC , entonces d ( B', C '  ) =  kd ( B, C ), C'B'A'   = ± CBA y A'C'B '   = ± ACB . ${\ Displaystyle \ angle}$${\ Displaystyle \ angle}$${\ Displaystyle \ angle}$ ${\ Displaystyle \ angle}$${\ Displaystyle \ angle}$${\ Displaystyle \ angle}$

Geometría de la escuela

George Bruce Halsted

Si es prudente o no enseñar geometría euclidiana desde un punto de vista axiomático al nivel de la escuela secundaria ha sido un tema de debate. Ha habido muchos intentos de hacerlo y no todos han tenido éxito. En 1904, George Bruce Halsted publicó un texto de geometría de la escuela secundaria basado en el conjunto de axiomas de Hilbert. Las críticas lógicas de este texto llevaron a una segunda edición muy revisada. Como reacción al lanzamiento del satélite ruso Sputnik, se hizo un llamamiento para revisar el plan de estudios de matemáticas de la escuela. De este esfuerzo surgió el programa New Math de la década de 1960. Con esto como trasfondo, muchos individuos y grupos se dispusieron a proporcionar material textual para clases de geometría basado en un enfoque axiomático.

Axiomas de Mac Lane

Saunders Mac Lane

Saunders Mac Lane (1909-2005), un matemático, escribió un artículo en 1959 en el que propuso un conjunto de axiomas para la geometría euclidiana en el espíritu del tratamiento de Birkhoff usando una función de distancia para asociar números reales con segmentos de línea. Este no fue el primer intento de basar un tratamiento a nivel escolar en el sistema de Birkhoff; de hecho, Birkhoff y Ralph Beatley habían escrito un texto de secundaria en 1940 que desarrolló la geometría euclidiana a partir de cinco axiomas y la capacidad de medir segmentos y ángulos de línea. Sin embargo, para orientar el tratamiento a una audiencia de la escuela secundaria, algunos argumentos matemáticos y lógicos fueron ignorados o arrastrados.

En el sistema de Mac Lane hay cuatro nociones primitivas (términos indefinidos): punto , distancia , línea y medida de ángulo . También hay 14 axiomas, cuatro que dan las propiedades de la función de distancia, cuatro que describen las propiedades de las líneas, cuatro que discuten los ángulos (que son ángulos dirigidos en este tratamiento), un axioma de similitud (esencialmente el mismo que el de Birkhoff) y un axioma de continuidad que puede utilizarse para derivar el teorema de la barra transversal y su inverso. El mayor número de axiomas tiene la ventaja pedagógica de hacer que las primeras pruebas en el desarrollo sean más fáciles de seguir y el uso de una métrica familiar permite un rápido avance a través del material básico de modo que los aspectos más "interesantes" del tema se puedan abordar antes.

Axiomas del SMSG (Grupo de Estudio de Matemáticas Escolares)

En la década de 1960, el Grupo de Estudio de Matemáticas Escolares (SMSG) introdujo un nuevo conjunto de axiomas para la geometría euclidiana, adecuado para los cursos de geometría de la escuela secundaria , como parte del nuevo plan de estudios de matemáticas . Este conjunto de axiomas sigue el modelo de Birkhoff de utilizar los números reales para acceder rápidamente a los fundamentos geométricos. Sin embargo, mientras Birkhoff trató de minimizar el número de axiomas utilizados, y la mayoría de los autores estaban preocupados por la independencia de los axiomas en sus tratamientos, la lista de axiomas SMSG se hizo intencionalmente grande y redundante por razones pedagógicas. El SMSG solo produjo un texto mimeografiado usando estos axiomas, pero Edwin E. Moise , un miembro del SMSG, escribió un texto de escuela secundaria basado en este sistema, y ​​un texto de nivel universitario, Moise (1974) , con algunas de las redundancias eliminadas. y modificaciones hechas a los axiomas para una audiencia más sofisticada.

Hay ocho términos indefinidos: punto , línea , plano , reposo , distancia , medida de ángulo , área y volumen . Los 22 axiomas de este sistema reciben nombres individuales para facilitar la referencia. Entre estos se encuentran: el Postulado de la regla, el Postulado de la colocación de la regla, el Postulado de la separación del plano, el Postulado de la suma de ángulos , el Postulado del ángulo lateral (SAS), el Postulado paralelo (en la forma de Playfair ) y el principio de Cavalieri .

Axiomas de UCSMP (Proyecto de Matemáticas Escolares de la Universidad de Chicago)

Aunque gran parte del nuevo plan de estudios de matemáticas se ha modificado o abandonado drásticamente, la parte de geometría se ha mantenido relativamente estable. Los libros de texto de las escuelas secundarias modernas utilizan sistemas de axiomas que son muy similares a los del SMSG. Por ejemplo, los textos producidos por el Proyecto de Matemáticas Escolares de la Universidad de Chicago (UCSMP) utilizan un sistema que, además de alguna actualización del lenguaje, se diferencia principalmente del sistema SMSG en que incluye algunos conceptos de transformación bajo su "Postulado de Reflexión".

Solo hay tres términos indefinidos: punto , línea y plano . Hay ocho "postulados", pero la mayoría de ellos tienen varias partes (que en este sistema se denominan generalmente supuestos ). Contando estas partes, hay 32 axiomas en este sistema. Entre los postulados se encuentran el postulado punto-línea-plano , el postulado de desigualdad del triángulo , los postulados de distancia, medida de ángulos, ángulos correspondientes, área y volumen, y el postulado de Reflexión. El postulado de reflexión se utiliza como reemplazo del postulado SAS del sistema SMSG.

Otros sistemas

Oswald Veblen (1880-1960) proporcionó un nuevo sistema de axiomas en 1904 cuando reemplazó el concepto de "intermediación", tal como lo usaron Hilbert y Pasch, por un nuevo orden primitivo . Esto permitió que varios términos primitivos usados ​​por Hilbert se convirtieran en entidades definidas, reduciendo el número de nociones primitivas a dos, punto y orden .

A lo largo de los años se han propuesto muchos otros sistemas axiomáticos para la geometría euclidiana. Se puede encontrar una comparación de muchos de estos en una monografía de 1927 de Henry George Forder. Forder también da, al combinar axiomas de diferentes sistemas, su propio tratamiento basado en las dos nociones primitivas de punto y orden . También proporciona un tratamiento más abstracto de uno de los sistemas de Pieri (de 1909) basado en el punto primitivo y la congruencia .

Comenzando con Peano, ha habido un hilo de interés paralelo entre los lógicos sobre los fundamentos axiomáticos de la geometría euclidiana. Esto se puede ver, en parte, en la notación utilizada para describir los axiomas. Pieri afirmó que a pesar de que escribió en el lenguaje tradicional de la geometría, siempre estaba pensando en términos de la notación lógica introducida por Peano, y usó ese formalismo para ver cómo probar las cosas. Un ejemplo típico de este tipo de notación se puede encontrar en el trabajo de EV Huntington (1874-1952) quien, en 1913, produjo un tratamiento axiomático de la geometría euclidiana tridimensional basado en las nociones primitivas de esfera e inclusión (una esfera que yace dentro de otro). Más allá de la notación, también hay interés en la estructura lógica de la teoría de la geometría. Alfred Tarski demostró que una parte de la geometría, a la que llamó geometría elemental , es una teoría lógica de primer orden (véanse los axiomas de Tarski ).

Los tratamientos textuales modernos de los fundamentos axiomáticos de la geometría euclidiana siguen el patrón de HG Forder y Gilbert de B. Robinson, quienes mezclan y combinan axiomas de diferentes sistemas para producir diferentes énfasis. Venema (2006) es un ejemplo moderno de este enfoque.

Geometría no euclidiana

En vista del papel que desempeñan las matemáticas en la ciencia y las implicaciones del conocimiento científico para todas nuestras creencias, los cambios revolucionarios en la comprensión del hombre de la naturaleza de las matemáticas no podían sino significar cambios revolucionarios en su comprensión de la ciencia, doctrinas filosóficas, religiosas y éticas. creencias y, de hecho, todas las disciplinas intelectuales.

En la primera mitad del siglo XIX tuvo lugar una revolución en el campo de la geometría que fue científicamente tan importante como la revolución copernicana en astronomía y tan filosóficamente profunda como la teoría darwiniana de la evolución en su impacto en la forma en que pensamos. Esta fue la consecuencia del descubrimiento de la geometría no euclidiana. Durante más de dos mil años, a partir de la época de Euclides, los postulados que fundamentan la geometría se consideraron verdades evidentes sobre el espacio físico. Los geómetras pensaron que estaban deduciendo de ellos otras verdades más oscuras, sin posibilidad de error. Esta visión se volvió insostenible con el desarrollo de la geometría hiperbólica. Ahora había dos sistemas de geometría incompatibles (y más tarde vinieron) que eran autoconsistentes y compatibles con el mundo físico observable. "A partir de este momento, toda la discusión sobre la relación entre geometría y espacio físico se llevó a cabo en términos bastante diferentes" ( Moise 1974 , p. 388).

Para obtener una geometría no euclidiana, el postulado paralelo (o su equivalente) debe reemplazarse por su negación . Negar la forma del axioma de Playfair , ya que es un enunciado compuesto (... existe uno y solo uno ...), se puede hacer de dos maneras. O existirá más de una línea a través del punto paralelo a la línea dada o no existirán líneas a través del punto paralelo a la línea dada. En el primer caso, reemplazando el postulado paralelo (o su equivalente) con el enunciado "En un plano, dado un punto P y una recta ℓ que no pasa por P, existen dos rectas que pasan por P que no se encuentran con ℓ " y se mantienen todos los otros axiomas, produce geometría hiperbólica . El segundo caso no se resuelve tan fácilmente. Simplemente reemplazando el postulado paralelo con el enunciado, "En un plano, dado un punto P y una línea ℓ que no pasa por P, todas las líneas que pasan por P se encuentran con ℓ ", no da un conjunto consistente de axiomas. Esto se sigue ya que las líneas paralelas existen en geometría absoluta, pero esta afirmación diría que no hay líneas paralelas. Este problema era conocido (en una forma diferente) por Khayyam, Saccheri y Lambert y fue la base para rechazar lo que se conoció como el "caso del ángulo obtuso". Para obtener un conjunto consistente de axiomas que incluya este axioma de no tener líneas paralelas, algunos de los otros axiomas deben modificarse. Los ajustes a realizar dependen del sistema de axiomas que se utilice. Entre otros, estos ajustes tendrán el efecto de modificar el segundo postulado de Euclides desde la afirmación de que los segmentos de línea pueden extenderse indefinidamente hasta la afirmación de que las líneas son ilimitadas. La geometría elíptica de Riemann surge como la geometría más natural que satisface este axioma.

Fue Gauss quien acuñó el término "geometría no euclidiana". Se refería a su propia obra inédita, que hoy llamamos geometría hiperbólica . Varios autores todavía consideran sinónimos "geometría no euclidiana" y "geometría hiperbólica". En 1871, Felix Klein , al adaptar una métrica discutida por Arthur Cayley en 1852, pudo llevar las propiedades métricas a un escenario proyectivo y así pudo unificar los tratamientos de la geometría hiperbólica, euclidiana y elíptica bajo el paraguas de la geometría proyectiva . Klein es responsable de los términos "hiperbólico" y "elíptico" (en su sistema llamó a la geometría euclidiana "parabólica", un término que no ha sobrevivido a la prueba del tiempo y se utiliza hoy sólo en algunas disciplinas). al uso común del término "geometría no euclidiana" para significar geometría "hiperbólica" o "elíptica".

Hay algunos matemáticos que ampliarían la lista de geometrías que deberían llamarse "no euclidianas" de varias formas. En otras disciplinas, sobre todo la física matemática , donde la influencia de Klein no fue tan fuerte, el término "no euclidiano" a menudo se considera que no significa euclidiano.

Postulado paralelo de Euclides

Durante dos mil años, se hicieron muchos intentos para probar el postulado paralelo utilizando los primeros cuatro postulados de Euclides. Una posible razón por la que tal prueba fue tan buscada fue que, a diferencia de los primeros cuatro postulados, el postulado paralelo no es evidente por sí mismo. Si el orden en que se enumeraron los postulados en los Elementos es significativo, indica que Euclides incluyó este postulado solo cuando se dio cuenta de que no podía probarlo ni proceder sin él. Se hicieron muchos intentos para probar el quinto postulado de los otros cuatro, muchos de ellos fueron aceptados como pruebas durante largos períodos de tiempo hasta que se encontró el error. Invariablemente, el error fue asumir alguna propiedad "obvia" que resultó ser equivalente al quinto postulado. Con el tiempo, se comprendió que este postulado puede no ser demostrable a partir de los otros cuatro. Según Trudeau (1987 , p. 154) esta opinión sobre el postulado paralelo (Postulado 5) aparece impresa:

Aparentemente, el primero en hacerlo fue GS Klügel (1739-1812), un estudiante de doctorado en la Universidad de Göttingen, con el apoyo de su maestro AG Kästner, en la disertación de 1763 del primero Conatuum praecipuorum theoriam paralelarum demostrandi recensio (Revisión de los más celebrados Intentos de demostrar la teoría de los paralelos). En este trabajo, Klügel examinó 28 intentos de probar el Postulado 5 (incluido el de Saccheri), los encontró todos deficientes y ofreció la opinión de que el Postulado 5 es indemostrable y está respaldado únicamente por el juicio de nuestros sentidos.

El comienzo del siglo XIX finalmente sería testigo de pasos decisivos en la creación de la geometría no euclidiana. Alrededor de 1813, Carl Friedrich Gauss e independientemente alrededor de 1818, el profesor de derecho alemán Ferdinand Karl Schweikart tenían las ideas germinales de la geometría no euclidiana elaboradas, pero ninguno publicó ningún resultado. Luego, alrededor de 1830, el matemático húngaro János Bolyai y el matemático ruso Nikolai Ivanovich Lobachevsky publicaron por separado tratados sobre lo que hoy llamamos geometría hiperbólica . En consecuencia, la geometría hiperbólica se ha denominado geometría Bolyai-Lobachevskiana, ya que ambos matemáticos, independientes entre sí, son los autores básicos de la geometría no euclidiana. Gauss mencionó al padre de Bolyai, cuando le mostró el trabajo del joven Bolyai, que había desarrollado tal geometría varios años antes, aunque no la publicó. Mientras Lobachevsky creó una geometría no euclidiana al negar el postulado paralelo, Bolyai elaboró ​​una geometría en la que tanto la geometría euclidiana como la hiperbólica son posibles dependiendo de un parámetro k . Bolyai termina su trabajo mencionando que no es posible decidir a través del razonamiento matemático solamente si la geometría del universo físico es euclidiana o no euclidiana; esta es una tarea de las ciencias físicas. La independencia del postulado paralelo de los otros axiomas de Euclides fue finalmente demostrada por Eugenio Beltrami en 1868.

Los diversos intentos de demostración del postulado paralelo produjeron una larga lista de teoremas que son equivalentes al postulado paralelo. La equivalencia aquí significa que en presencia de los otros axiomas de la geometría se puede suponer que cada uno de estos teoremas es verdadero y el postulado paralelo se puede probar a partir de este conjunto alterado de axiomas. Esto no es lo mismo que la equivalencia lógica . En diferentes conjuntos de axiomas para la geometría euclidiana, cualquiera de estos puede reemplazar el postulado paralelo euclidiano. La siguiente lista parcial indica algunos de estos teoremas que son de interés histórico.

1. Las líneas rectas paralelas son equidistantes. (Poseidonios, siglo I a.C.)
2. Todos los puntos equidistantes de una línea recta dada, en un lado dado de ella, constituyen una línea recta. (Christoph Clavius, 1574)
3. El axioma de Playfair . En un plano, hay como máximo una línea que se puede trazar paralela a otra dada a través de un punto externo. (Proclo, siglo V, pero popularizado por John Playfair, finales del siglo XVIII)
4. La suma de los ángulos en cada triángulo es 180 ° (Gerolamo Saccheri, 1733; Adrien-Marie Legendre, principios del siglo XIX)
5. Existe un triángulo cuyos ángulos suman 180 °. (Gerolamo Saccheri, 1733; Adrien-Marie Legendre, principios del siglo XIX)
6. Existe un par de triángulos similares , pero no congruentes . (Gerolamo Saccheri, 1733)
7. Cada triángulo se puede circunscribir . (Adrien-Marie Legendre, Farkas Bolyai, principios del siglo XIX)
8. Si tres ángulos de un cuadrilátero son ángulos rectos , entonces el cuarto ángulo también es un ángulo recto. (Alexis-Claude Clairaut, 1741; Johann Heinrich Lambert, 1766)
9. Existe un cuadrilátero en el que todos los ángulos son ángulos rectos. (Geralamo Saccheri, 1733)
10. Postulado de Wallis . En una línea recta finita dada siempre es posible construir un triángulo similar a un triángulo dado. (John Wallis, 1663; Lazare-Nicholas-Marguerite Carnot, 1803; Adrien-Marie Legendre, 1824)
11. No hay límite superior para el área de un triángulo. (Carl Friedrich Gauss, 1799)
12. Los ángulos de la cumbre del cuadrilátero de Saccheri son 90 °. (Geralamo Saccheri, 1733)
13. Axioma de Proclo . Si una línea se cruza con una de dos líneas paralelas, ambas coplanares con la línea original, entonces también se cruza con la otra. (Proclo, siglo V)

Geometría neutra (o absoluta)

La geometría absoluta es una geometría basada en un sistema de axiomas que consta de todos los axiomas que dan la geometría euclidiana excepto el postulado paralelo o cualquiera de sus alternativas. El término fue introducido por János Bolyai en 1832. A veces se le llama geometría neutra , ya que es neutra con respecto al postulado paralelo.

Relación con otras geometrías

En los Elementos de Euclides , las primeras 28 proposiciones y la Proposición I.31 evitan el uso del postulado paralelo y, por lo tanto, son teoremas válidos en geometría absoluta. La propuesta I.31 prueba la existencia de líneas paralelas (por construcción). Además, se puede demostrar el teorema de Saccheri-Legendre , que establece que la suma de los ángulos de un triángulo es como máximo 180 °.

Los teoremas de la geometría absoluta se mantienen tanto en la geometría hiperbólica como en la euclidiana .

La geometría absoluta es incompatible con la geometría elíptica : en la geometría elíptica no hay líneas paralelas en absoluto, pero en la geometría absoluta existen líneas paralelas. Además, en geometría elíptica, la suma de los ángulos en cualquier triángulo es mayor que 180 °.

Incompletitud

Lógicamente, los axiomas no forman una teoría completa, ya que se pueden agregar axiomas independientes adicionales sin hacer que el sistema de axiomas sea inconsistente. Se puede extender la geometría absoluta agregando diferentes axiomas sobre el paralelismo y obtener sistemas de axiomas incompatibles pero consistentes, dando lugar a la geometría euclidiana o hiperbólica. Por tanto, todo teorema de geometría absoluta es un teorema de geometría hiperbólica y geometría euclidiana. Sin embargo, lo contrario no es cierto. Además, la geometría absoluta no es una teoría categórica , ya que tiene modelos que no son isomorfos.

Geometría hiperbólica

En el enfoque axiomático de la geometría hiperbólica (también conocida como geometría lobachevskiana o geometría bolyai-lobachevskiana), se agrega un axioma adicional a los axiomas que dan la geometría absoluta . El nuevo axioma es el postulado paralelo de Lobachevsky (también conocido como el postulado característico de la geometría hiperbólica ):

A través de un punto que no está en una línea dada, existen (en el plano determinado por este punto y línea) al menos dos líneas que no se encuentran con la línea dada.

Con esta adición, el sistema axiom ahora está completo.

Aunque el nuevo axioma afirma solo la existencia de dos líneas, se establece fácilmente que hay un número infinito de líneas a través del punto dado que no se encuentran con la línea dada. Dada esta plenitud, uno debe tener cuidado con la terminología en este contexto, ya que el término línea paralela ya no tiene el significado único que tiene en la geometría euclidiana. Específicamente, sea P un punto que no está en una línea dada . Sea PA la perpendicular trazada desde P hasta (encuentro en el punto A ). Las líneas que pasan por P se dividen en dos clases, las que se encuentran y las que no. El postulado característico de la geometría hiperbólica dice que hay al menos dos líneas de este último tipo. De las líneas que no se encuentran , habrá (a cada lado de PA ) una línea que forma el ángulo más pequeño con PA . A veces, estas líneas se conocen como las primeras líneas a través de P que no se encuentran y se denominan de forma diversa líneas limitantes, asintóticas o paralelas (cuando se usa este último término, estas son las únicas líneas paralelas). Todas las demás líneas que pasan por P y que no se encuentran se denominan líneas que no se cruzan o ultraparalelas . ${\ Displaystyle \ ell}$${\ Displaystyle \ ell}$${\ Displaystyle \ ell}$${\ Displaystyle \ ell}$${\ Displaystyle \ ell}$${\ Displaystyle \ ell}$

Dado que la geometría hiperbólica y la geometría euclidiana se basan en los axiomas de la geometría absoluta, comparten muchas propiedades y proposiciones. Sin embargo, las consecuencias de reemplazar el postulado paralelo de la geometría euclidiana por el postulado característico de la geometría hiperbólica pueden ser dramáticas. Para mencionar algunos de estos:

Cuadrilátero de Lambert en geometría hiperbólica

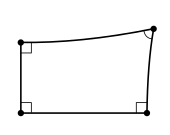
• Un cuadrilátero de Lambert es un cuadrilátero que tiene tres ángulos rectos. El cuarto ángulo de un cuadrilátero de Lambert es agudo si la geometría es hiperbólica y un ángulo recto si la geometría es euclidiana. Además, los rectángulos pueden existir (un enunciado equivalente al postulado paralelo) solo en la geometría euclidiana.
• Un cuadrilátero de Saccheri es un cuadrilátero que tiene dos lados de igual longitud, ambos perpendiculares a un lado llamado base . Los otros dos ángulos de un cuadrilátero de Saccheri se llaman ángulos de la cumbre y tienen la misma medida. Los ángulos de la cumbre de un cuadrilátero de Saccheri son agudos si la geometría es hiperbólica y ángulos rectos si la geometría es euclidiana.
• La suma de las medidas de los ángulos de cualquier triángulo es menor que 180 ° si la geometría es hiperbólica, e igual a 180 ° si la geometría es euclidiana. El defecto de un triángulo es el valor numérico (180 ° - suma de las medidas de los ángulos del triángulo). Este resultado también puede expresarse como: el defecto de los triángulos en la geometría hiperbólica es positivo y el defecto de los triángulos en la geometría euclidiana es cero.
• El área de un triángulo en geometría hiperbólica está acotada, mientras que existen triángulos con áreas arbitrariamente grandes en geometría euclidiana.
• El conjunto de puntos en el mismo lado e igualmente lejos de una línea recta dada forman ellos mismos una línea en la geometría euclidiana, pero no en la geometría hiperbólica (forman un hiperciclo ).

Los defensores de la posición de que la geometría euclidiana es la única geometría "verdadera" recibieron un revés cuando, en un libro de memorias publicado en 1868, "Teoría fundamental de los espacios de curvatura constante", Eugenio Beltrami dio una prueba abstracta de la equiconsistencia de la geometría hiperbólica y euclidiana. geometría para cualquier dimensión. Lo logró al introducir varios modelos de geometría no euclidiana que ahora se conocen como el modelo de Beltrami-Klein , el modelo de disco de Poincaré y el modelo de medio plano de Poincaré , junto con transformaciones que los relacionan. Para el modelo de semiplano, Beltrami citó una nota de Liouville en el tratado de Monge sobre geometría diferencial . Beltrami también mostró que la geometría euclidiana n- dimensional se realiza en una horósfera del espacio hiperbólico ( n  + 1) -dimensional , por lo que la relación lógica entre la consistencia de las geometrías euclidiana y no euclidiana es simétrica.

Geometría elíptica

Otra forma de modificar el postulado de las paralelas euclidianas es asumir que no hay líneas paralelas en un plano. A diferencia de la situación con la geometría hiperbólica , donde solo agregamos un nuevo axioma, no podemos obtener un sistema consistente agregando este enunciado como un nuevo axioma a los axiomas de la geometría absoluta . Esto se sigue ya que las líneas paralelas probablemente existen en geometría absoluta. Hay que cambiar otros axiomas.

Comenzando con los axiomas de Hilbert, los cambios necesarios implican eliminar los cuatro axiomas de orden de Hilbert y reemplazarlos con estos siete axiomas de separación relacionados con una nueva relación indefinida.

Hay una relación indefinida ( primitiva ) entre cuatro puntos, A , B , C y D denotados por ( A , C | B , D ) y leídos como " A y C separan B y D ", satisfaciendo estos axiomas:

1. Si ( A , B | C , D ), entonces los puntos A , B , C y D son colineales y distintos.
2. Si ( A , B | C , D ), entonces ( C , D | A , B ) y ( B , A | D , C ).
3. Si ( A , B | C , D ), entonces no ( A , C | B , D ).
4. Si los puntos A , B , C y D son colineales y distintos, entonces ( A , B | C , D ) o ( A , C | B , D ) o ( A , D | B , C ).
5. Si los puntos A , B y C son colineales y distintos, entonces existe un punto D tal que ( A , B | C , D ).
6. Para cinco puntos colineales distintos A , B , C , D y E , si ( A , B | D , E ), entonces ( A , B | C , D ) o ( A , B | C , E ).
7. Las perspectivas preservan la separación.

Dado que se ha eliminado la noción de Hilbert de "intermediación", es necesario redefinir los términos que se definieron utilizando ese concepto. Por lo tanto, es necesario reformular un segmento de línea AB definido como los puntos A y B y todos los puntos entre A y B en geometría absoluta. Un segmento de línea en esta nueva geometría está determinada por tres puntos colineales A , B y C y se compone de esos tres puntos y todos los puntos no separado de B por A y C . Hay más consecuencias. Dado que dos puntos no determinan un segmento de línea de forma única, tres puntos no colineales no determinan un triángulo único, y la definición de triángulo debe reformularse.

Una vez redefinidas estas nociones, los otros axiomas de la geometría absoluta (incidencia, congruencia y continuidad) cobran sentido y quedan tranquilos. Junto con el nuevo axioma sobre la inexistencia de líneas paralelas, tenemos un sistema consistente de axiomas que dan una nueva geometría. La geometría resultante se llama geometría elíptica (plana) .

Cuadriláteros de Saccheri en geometría euclidiana, elíptica e hiperbólica

Aunque la geometría elíptica no es una extensión de la geometría absoluta (como lo son la geometría euclidiana e hiperbólica), hay una cierta "simetría" en las proposiciones de las tres geometrías que refleja una conexión más profunda que fue observada por Felix Klein. Algunas de las proposiciones que exhiben esta propiedad son:

• El cuarto ángulo de un cuadrilátero de Lambert es un ángulo obtuso en geometría elíptica.
• Los ángulos de la cumbre de un cuadrilátero de Saccheri son obtusos en geometría elíptica.
• La suma de las medidas de los ángulos de cualquier triángulo es mayor que 180 ° si la geometría es elíptica. Es decir, el defecto de un triángulo es negativo.
• Todas las líneas perpendiculares a una línea dada se encuentran en un punto común en la geometría elíptica, llamado polo de la línea. En la geometría hiperbólica, estas líneas no se cruzan mutuamente, mientras que en la geometría euclidiana son mutuamente paralelas.

Otros resultados, como el teorema del ángulo exterior , enfatizan claramente la diferencia entre las geometrías elípticas y las que son extensiones de la geometría absoluta.

Geometría esférica

Otras geometrías

Geometría proyectiva

Geometría afín

Geometría ordenada

La geometría absoluta es una extensión de la geometría ordenada y, por lo tanto, todos los teoremas de la geometría ordenada se mantienen en la geometría absoluta. Lo contrario no es cierto. La geometría absoluta asume los primeros cuatro axiomas de Euclides (o sus equivalentes), para contrastarlos con la geometría afín , que no asume el tercer y cuarto axiomas de Euclides. La geometría ordenada es una base común de la geometría absoluta y afín.

Geometría finita

Ver también

• Sin coordenadas
• Geometría sintética

Notas

Referencias

• Bola, WW Rouse (1960). A Short Account of the History of Mathematics (4ª ed. [Reimpresión. Publicación original: Londres: Macmillan & Co., 1908] ed.). Nueva York: Publicaciones de Dover. págs.  50–62 . ISBN 0-486-20630-0.
• Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Geometría proyectiva: de los cimientos a las aplicaciones , Cambridge University Press , ISBN 978-0-521-48364-3, MR  1629468
• Eves, Howard (1963), A Survey of Geometry (Volumen uno) , Boston: Allyn y Bacon
• Faber, Richard L. (1983), Fundamentos de la geometría euclidiana y no euclidiana , Nueva York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
• Greenberg, Marvin Jay (2007), Geometrías euclidianas y no euclidianas / Desarrollo e historia, 4a edición , San Francisco: WH Freeman, ISBN 978-0716799481
• Heath, Thomas L. (1956). Los trece libros de los elementos de Euclides (2ª ed. [Facsímil. Publicación original: Cambridge University Press, 1925] ed.). Nueva York: Publicaciones de Dover.

(3 vols.): ISBN  0-486-60088-2 (vol. 1), ISBN  0-486-60089-0 (vol. 2), ISBN  0-486-60090-4 (vol. 3).

• Hilbert, David (1950) [publicado por primera vez en 1902], The Foundations of Geometry [Grundlagen der Geometrie] (PDF) , traducción al inglés de EJ Townsend (2ª ed.), La Salle, IL: Open Court Publishing
• Hilbert, David (1990) [1971], Foundations of Geometry [Grundlagen der Geometrie] , traducido por Leo Unger de la 10ª edición alemana (2ª ed. En inglés), La Salle, IL: Open Court Publishing, ISBN 0-87548-164-7
• Moise, Edwin E. (1974), Geometría elemental desde un punto de vista avanzado (2ª ed.), Reading, MA: Addison – Wesley, ISBN 0-201-04793-4
• Peano, Giuseppe (1889), I principii di geometria: logicamente esposti , Turín: Fratres Bocca
• Russell, Bertrand (1897) Un ensayo sobre los fundamentos de la geometría , a través de Internet Archive
• Trudeau, Richard J. (1987), La revolución no euclidiana , Boston: Birkhauser, ISBN 0-8176-3311-1
• Venema, Gerard A. (2006), Fundamentos de la geometría , Upper Saddle River, Nueva Jersey: Pearson Prentice Hall, ISBN 0-13-143700-3
• Wylie Jr., CR (1964), Foundations of Geometry , Nueva York: McGraw – Hill

enlaces externos

• O'Connor, John J .; Robertson, Edmund F. , "Moritz Pasch" , archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
• A. Seidenberg (2008). "Pasch, Moritz" . Diccionario completo de biografía científica . Consultado el 25 de agosto de 2013 .
• Moritz Pasch en el Proyecto de genealogía matemática
• O'Connor, John J .; Robertson, Edmund F. , "Giuseppe Peano" , archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
• Hubert Kennedy (2002). "Doce artículos sobre Giuseppe Peano" (PDF) . San Francisco: Publicaciones perentorias . Consultado el 8 de abril de 2012 . Colección de artículos sobre la vida y las matemáticas de Peano (años 1960 a 1980).
• Giuseppe Peano en el Proyecto de genealogía matemática
• O'Connor, John J .; Robertson, Edmund F. , "Mario Pieri" , archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
• Hubert Kennedy. "Pieri, Mario" . Diccionario completo de biografía científica . Consultado el 26 de agosto de 2013 .
• Axiomas de SMSG