Integral exponencial - Exponential integral

En matemáticas, la integral exponencial Ei es una función especial en el plano complejo . Se define como una integral definida particular de la razón entre una función exponencial y su argumento .

Definiciones

Para valores reales distintos de cero de  x , la integral exponencial Ei ( x ) se define como

${\ Displaystyle \ operatorname {Ei} (x) = - \ int _ {- x} ^ {\ infty} {\ frac {e ^ {- t}} {t}} \, dt = \ int _ {- \ infty} ^ {x} {\ frac {e ^ {t}} {t}} \, dt.}$

El algoritmo de Risch muestra que Ei no es una función elemental . La definición anterior se puede utilizar para valores positivos de  x , pero la integral debe entenderse en términos del valor principal de Cauchy debido a la singularidad del integrando en cero.

Para valores complejos del argumento, la definición se vuelve ambigua debido a los puntos de bifurcación en 0 y . En lugar de Ei, se usa la siguiente notación, ${\ Displaystyle \ infty}$

${\ Displaystyle E_ {1} (z) = \ int _ {z} ^ {\ infty} {\ frac {e ^ {- t}} {t}} \, dt, \ qquad | {\ rm {Arg} } (z) | <\ pi}$

Para valores positivos de  x , tenemos .${\ Displaystyle -E_ {1} (x) = \ operatorname {Ei} (-x)}$

En general, un corte de rama se toma en el eje real negativo y E ₁ puede definirse mediante la continuación analítica en cualquier otro lugar del plano complejo.

Para valores positivos de la parte real de , esto se puede escribir ${\ Displaystyle z}$

${\ Displaystyle E_ {1} (z) = \ int _ {1} ^ {\ infty} {\ frac {e ^ {- tz}} {t}} \, dt = \ int _ {0} ^ {1 } {\ frac {e ^ {- z / u}} {u}} \, du, \ qquad \ Re (z) \ geq 0.}$

El comportamiento de E ₁ cerca del corte de la rama se puede ver por la siguiente relación:

${\ Displaystyle \ lim _ {\ delta \ to 0+} E_ {1} (- x \ pm i \ delta) = - \ operatorname {Ei} (x) \ mp i \ pi, \ qquad x> 0.}$

Propiedades

Varias propiedades de la integral exponencial a continuación, en ciertos casos, permiten evitar su evaluación explícita a través de la definición anterior.

Serie convergente

Para argumentos reales o complejos fuera del eje real negativo, se puede expresar como ${\ Displaystyle E_ {1} (z)}$

${\ Displaystyle E_ {1} (z) = - \ gamma - \ ln z- \ sum _ {k = 1} ^ {\ infty} {\ frac {(-z) ^ {k}} {k \; k !}} \ qquad (\ left | \ operatorname {Arg} (z) \ right | <\ pi)}$

donde es la constante de Euler-Mascheroni . La suma converge para todos los complejos y tomamos el valor habitual del logaritmo complejo que tiene una rama cortada a lo largo del eje real negativo. ${\ Displaystyle \ gamma}$${\ Displaystyle z}$

Esta fórmula se puede utilizar para calcular con operaciones de coma flotante para valores reales entre 0 y 2,5. Porque , el resultado es inexacto debido a la cancelación . ${\ Displaystyle E_ {1} (x)}$${\ Displaystyle x}$${\ Displaystyle x> 2.5}$

Ramanujan encontró una serie convergente más rápida :

${\ Displaystyle {\ rm {Ei}} (x) = \ gamma + \ ln x + \ exp {(x / 2)} \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n-1} x ^ {n}} {n! \, 2 ^ {n-1}}} \ sum _ {k = 0} ^ {\ lfloor (n-1) / 2 \ rfloor} {\ frac {1} {2k + 1}}}$

Estas series alternas también se pueden usar para dar buenos límites asintóticos para x pequeña, por ejemplo:

${\ Displaystyle 1 - {\ frac {3x} {4}} \ leq {\ rm {Ei}} (x) - \ gamma - \ ln x \ leq 1 - {\ frac {3x} {4}} + { \ frac {11x ^ {2}} {36}}}$

para . ${\ Displaystyle x \ geq 0}$

Serie asintótica (divergente)

Desafortunadamente, la convergencia de la serie anterior es lenta para argumentos de módulo mayor. Por ejemplo, para x  = 10 se requieren más de 40 términos para obtener una respuesta correcta a tres cifras significativas para . Sin embargo, existe una aproximación de series divergentes que se puede obtener integrando por partes: ${\ Displaystyle E_ {1} (z)}$${\ Displaystyle ze ^ {z} E_ {1} (z)}$

${\ Displaystyle E_ {1} (z) = {\ frac {\ exp (-z)} {z}} \ sum _ {n = 0} ^ {N-1} {\ frac {n!} {(- z) ^ {n}}}}$

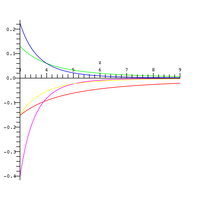
que tiene error de orden y es válido para valores grandes de . El error relativo de la aproximación anterior se representa en la figura de la derecha para varios valores de , el número de términos en la suma truncada ( en rojo, en rosa). ${\ Displaystyle O (N! z ^ {- N})}$${\ Displaystyle \ operatorname {Re} (z)}$${\ Displaystyle N}$${\ Displaystyle N = 1}$${\ Displaystyle N = 5}$

Comportamiento exponencial y logarítmico: horquillado

De las dos series sugeridas en subsecciones anteriores, se deduce que se comporta como una exponencial negativa para valores grandes del argumento y como un logaritmo para valores pequeños. Para valores reales positivos del argumento, se puede poner entre corchetes por funciones elementales de la siguiente manera: ${\ Displaystyle E_ {1}}$${\ Displaystyle E_ {1}}$

${\ Displaystyle {\ frac {1} {2}} e ^ {- x} \, \ ln \! \ left (1 + {\ frac {2} {x}} \ right) <E_ {1} (x ) <e ^ {- x} \, \ ln \! \ left (1 + {\ frac {1} {x}} \ right) \ qquad x> 0}$

El lado izquierdo de esta desigualdad se muestra en el gráfico de la izquierda en azul; la parte central se muestra en negro y el lado derecho se muestra en rojo. ${\ Displaystyle E_ {1} (x)}$

Definición de Ein

Ambos y se pueden escribir de forma más sencilla utilizando toda la función definida como ${\ Displaystyle \ operatorname {Ei}}$${\ Displaystyle E_ {1}}$ ${\ Displaystyle \ operatorname {Ein}}$

${\ Displaystyle \ operatorname {Ein} (z) = \ int _ {0} ^ {z} (1-e ^ {- t}) {\ frac {dt} {t}} = \ sum _ {k = 1 } ^ {\ infty} {\ frac {(-1) ^ {k + 1} z ^ {k}} {k \; k!}}}$

(tenga en cuenta que esta es solo la serie alterna en la definición anterior de ). Entonces tenemos ${\ Displaystyle \ mathrm {E} _ {1}}$

${\ Displaystyle E_ {1} (z) \, = \, - \ gamma - \ ln z + {\ rm {Ein}} (z) \ qquad \ left | \ operatorname {Arg} (z) \ right | <\ Pi }$

${\ Displaystyle \ operatorname {Ei} (x) \, = \, \ gamma + \ ln x- \ operatorname {Ein} (-x) \ qquad x> 0}$

Relación con otras funciones

Ecuación de Kummer

${\ Displaystyle z {\ frac {d ^ {2} w} {dz ^ {2}}} + (bz) {\ frac {dw} {dz}} - aw = 0}$

generalmente se resuelve mediante las funciones hipergeométricas confluentes y Pero cuando y eso es, ${\ Displaystyle M (a, b, z)}$${\ Displaystyle U (a, b, z).}$${\ Displaystyle a = 0}$${\ Displaystyle b = 1,}$

${\ Displaystyle z {\ frac {d ^ {2} w} {dz ^ {2}}} + (1-z) {\ frac {dw} {dz}} = 0}$

tenemos

${\ Displaystyle M (0,1, z) = U (0,1, z) = 1}$

para todo z . Entonces, E ₁ (- z ) da una segunda solución . De hecho,

${\ Displaystyle E_ {1} (- z) = - \ gamma -i \ pi + {\ frac {\ parcial [U (a, 1, z) -M (a, 1, z)]} {\ parcial a }}, \ qquad 0 <{\ rm {Arg}} (z) <2 \ pi}$

con la derivada evaluada en Otra conexión con las funciones hipergeométricas confluentes es que E ₁ es una exponencial multiplicada por la función U (1,1, z ): ${\ Displaystyle a = 0.}$

${\ Displaystyle E_ {1} (z) = e ^ {- z} U (1,1, z)}$

La integral exponencial está estrechamente relacionada con la función integral logarítmica li ( x ) por la fórmula

${\ Displaystyle \ operatorname {li} (e ^ {x}) = \ operatorname {Ei} (x)}$

para valores reales distintos de cero de . ${\ Displaystyle x}$

Generalización

La integral exponencial también se puede generalizar a

${\ Displaystyle E_ {n} (x) = \ int _ {1} ^ {\ infty} {\ frac {e ^ {- xt}} {t ^ {n}}} \, dt,}$

que se puede escribir como un caso especial de la función gamma incompleta :

${\ Displaystyle E_ {n} (x) = x ^ {n-1} \ Gamma (1-n, x).}$

La forma generalizada a veces se denomina función Misra , definida como ${\ Displaystyle \ varphi _ {m} (x)}$

${\ Displaystyle \ varphi _ {m} (x) = E _ {- m} (x).}$

Muchas propiedades de esta forma generalizada se pueden encontrar en la Biblioteca digital de funciones matemáticas del NIST.

La inclusión de un logaritmo define la función integro-exponencial generalizada

${\ Displaystyle E_ {s} ^ {j} (z) = {\ frac {1} {\ Gamma (j + 1)}} \ int _ {1} ^ {\ infty} \ left (\ log t \ right ) ^ {j} {\ frac {e ^ {- zt}} {t ^ {s}}} \, dt.}$

La integral indefinida:

${\ Displaystyle \ operatorname {Ei} (a \ cdot b) = \ iint e ^ {ab} \, da \, db}$

es similar en forma a la función generadora ordinaria para el número de divisores de : ${\ Displaystyle d (n)}$${\ Displaystyle n}$

${\ Displaystyle \ sum \ limits _ {n = 1} ^ {\ infty} d (n) x ^ {n} = \ sum \ limits _ {a = 1} ^ {\ infty} \ sum \ limits _ {b = 1} ^ {\ infty} x ^ {ab}}$

Derivados

Las derivadas de las funciones generalizadas se pueden calcular mediante la fórmula ${\ Displaystyle E_ {n}}$

${\ Displaystyle E_ {n} '(z) = - E_ {n-1} (z) \ qquad (n = 1,2,3, \ ldots)}$

Tenga en cuenta que la función es fácil de evaluar (lo que hace que esta recursión sea útil), ya que es solo . ${\ Displaystyle E_ {0}}$${\ Displaystyle e ^ {- z} / z}$

Integral exponencial de argumento imaginario

Si es imaginario, tiene una parte real no negativa, por lo que podemos usar la fórmula ${\ Displaystyle z}$

${\ Displaystyle E_ {1} (z) = \ int _ {1} ^ {\ infty} {\ frac {e ^ {- tz}} {t}} \, dt}$

para obtener una relación con las integrales trigonométricas y : ${\ Displaystyle \ operatorname {Si}}$${\ Displaystyle \ operatorname {Ci}}$

${\ Displaystyle E_ {1} (ix) = i \ left [- {\ tfrac {1} {2}} \ pi + \ operatorname {Si} (x) \ right] - \ operatorname {Ci} (x) \ qquad (x> 0)}$

Las partes reales e imaginarias de están representadas en la figura de la derecha con curvas negras y rojas. ${\ Displaystyle \ mathrm {E} _ {1} (ix)}$

Aproximaciones

Ha habido varias aproximaciones para la función integral exponencial. Éstos incluyen:

• La aproximación de Swamee y Ohija
  $${\ Displaystyle E_ {1} (x) = \ left (A ^ {- 7.7} + B \ right) ^ {- 0.13},}$$

  
  dónde
  $${\ displaystyle {\ begin {alineado} A & = \ ln \ left [\ left ({\ frac {0.56146} {x}} + 0.65 \ right) (1 + x) \ right] \\ B & = x ^ {4 } e ^ {7.7x} (2 + x) ^ {3.7} \ end {alineado}}}$$

  
• La aproximación de Allen y Hastings
  $${\ Displaystyle E_ {1} (x) = {\ begin {cases} - \ ln x + {\ textbf {a}} ^ {T} {\ textbf {x}} _ {5}, & x \ leq 1 \\ {\ frac {e ^ {- x}} {x}} {\ frac {{\ textbf {b}} ^ {T} {\ textbf {x}} _ {3}} {{\ textbf {c}} ^ {T} {\ textbf {x}} _ {3}}}, & x \ geq 1 \ end {cases}}}$$

  
  dónde
  $${\ displaystyle {\ begin {alineado} {\ textbf {a}} & \ triangleq [-0.57722,0.99999, -0.24991,0.05519, -0.00976,0.00108] ^ {T} \\ {\ textbf {b}} & \ triangleq [0.26777,8.63476,18.05902,8.57333] ^ {T} \\ {\ textbf {c}} & \ triangleq [3.95850,21.09965,25.63296,9.57332] ^ {T} \\ {\ textbf {x}} _ { k} & \ triangleq [x ^ {0}, x ^ {1}, \ dots, x ^ {k}] ^ {T} \ end {alineado}}}$$

  
• La expansión continua de la fracción
  $${\ Displaystyle E_ {1} (x) = {\ cfrac {e ^ {- x}} {x + {\ cfrac {1} {1 + {\ cfrac {1} {x + {\ cfrac {2} {1+ {\ cfrac {2} {x + {\ cfrac {3} {\ ddots}}}}}}}}}}}.}$$

  
• La aproximación de Barry et al.
  $${\ Displaystyle E_ {1} (x) = {\ frac {e ^ {- x}} {G + (1-G) e ^ {- {\ frac {x} {1-G}}}}} \ ln \ left [1 + {\ frac {G} {x}} - {\ frac {1-G} {(h + bx) ^ {2}}} \ right],}$$

  
  dónde:
  $${\ Displaystyle {\ begin {alineado} h & = {\ frac {1} {1 + x {\ sqrt {x}}}} + {\ frac {h _ {\ infty} q} {1 + q}} \\ q & = {\ frac {20} {47}} x ^ {\ sqrt {\ frac {31} {26}}} \\ h _ {\ infty} & = {\ frac {(1-G) (G ^ { 2} -6G + 12)} {3G (2-G) ^ {2} b}} \\ b & = {\ sqrt {\ frac {2 (1-G)} {G (2-G)}}} \\ G & = e ^ {- \ gamma} \ end {alineado}}}$$

  
  con siendo la constante de Euler-Mascheroni .${\ Displaystyle \ gamma}$

Aplicaciones

• Transferencia de calor dependiente del tiempo
• Flujo de agua subterránea sin equilibrio en la solución de Theis (llamada función de pozo )
• Transferencia radiativa en atmósferas estelares y planetarias
• Ecuación de difusividad radial para flujo en estado transitorio o inestable con fuentes de línea y sumideros
• Soluciones a la ecuación de transporte de neutrones en geometrías 1-D simplificadas

Ver también

• Integral de Goodwin-Staton
• Funciones de Bickley-Naylor

Notas

Referencias

• Abramowitz, Milton; Irene Stegun (1964). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Abramowitz y Stegun . Nueva York: Dover. ISBN 978-0-486-61272-0., Capítulo 5 .
• Bender, Carl M .; Steven A. Orszag (1978). Métodos matemáticos avanzados para científicos e ingenieros . McGraw – Hill. ISBN 978-0-07-004452-4.
• Bleistein, Norman; Richard A. Handelsman (1986). Expansiones asintóticas de integrales . Dover. ISBN 978-0-486-65082-1.
• Busbridge, Ida W. (1950). "Sobre la función integro-exponencial y la evaluación de algunas integrales que la involucran". Cuarto de galón. J. Math. (Oxford) . 1 (1): 176–184. Código Bib : 1950QJMat ... 1..176B . doi : 10.1093 / qmath / 1.1.176 .
• Stankiewicz, A. (1968). "Tablas de las funciones integro-exponenciales". Acta Astronomica . 18 : 289. Bibcode : 1968AcA .... 18..289S .
• Sharma, RR; Zohuri, Bahman (1977). "Un método general para una evaluación precisa de integrales exponenciales E ₁ (x), x> 0". J. Comput. Phys . 25 (2): 199–204. Código bibliográfico : 1977JCoPh..25..199S . doi : 10.1016 / 0021-9991 (77) 90022-5 .
• Kölbig, KS (1983). "En la integral exp (- μt ) t ^{ν − 1} log ^m t  dt " . Matemáticas. Computación . 41 (163): 171–182. doi : 10.1090 / S0025-5718-1983-0701632-1 .
• Milgram, MS (1985). "La función integro-exponencial generalizada" . Matemáticas de la Computación . 44 (170): 443–458. doi : 10.1090 / S0025-5718-1985-0777276-4 . JSTOR  2007964 . Señor  0777276 .
• Misra, Rama Dhar; Nacido, M. (1940). "Sobre la estabilidad de Crystal Lattices. II". Procedimientos matemáticos de la Sociedad Filosófica de Cambridge . 36 (2): 173. Código Bibliográfico : 1940PCPS ... 36..173M . doi : 10.1017 / S030500410001714X .
• Chiccoli, C .; Lorenzutta, S .; Maino, G. (1988). "Sobre la evaluación de integrales exponenciales generalizadas E _ν (x)". J. Comput. Phys . 78 (2): 278–287. Código bibliográfico : 1988JCoPh..78..278C . doi : 10.1016 / 0021-9991 (88) 90050-2 .
• Chiccoli, C .; Lorenzutta, S .; Maino, G. (1990). "Resultados recientes para integrales exponenciales generalizadas" . Matemáticas informáticas. Applic . 19 (5): 21-29. doi : 10.1016 / 0898-1221 (90) 90098-5 .
• MacLeod, Allan J. (2002). "El cálculo eficiente de algunas integrales exponenciales generalizadas" . J. Comput. Apl. Matemáticas . 148 (2): 363–374. Código bibliográfico : 2002JCoAm.138..363M . doi : 10.1016 / S0377-0427 (02) 00556-3 .
• Presione, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 6.3. Integrales exponenciales" , Recetas numéricas: El arte de la informática científica (3ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-521-88068-8
• Temme, NM (2010), "Integrales exponenciales, logarítmicas, seno y coseno" , en Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR  2723248

enlaces externos

• "Función exponencial integral" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Documentación del NIST sobre la integral exponencial generalizada
• Weisstein, Eric W. "Integral exponencial" . MathWorld .
• Weisstein, Eric W. " En- Función" . MathWorld .
• "Integral exponencial Ei" . Sitio de Wolfram Functions.
• Integrales exponencial, logarítmica, seno y coseno en DLMF .