Castor ocupado - Busy beaver
En la informática teórica , el atareado juego del castor tiene como objetivo encontrar un programa final de un tamaño determinado que produzca el mayor rendimiento posible. Dado que un programa en bucle sin fin que produce una salida infinita se concibe fácilmente, tales programas se excluyen del juego.
Más precisamente, el ajetreado juego del castor consiste en diseñar una máquina de Turing de alfabeto binario que se detiene y que escribe la mayor cantidad de 1 en la cinta, utilizando solo un conjunto determinado de estados. Las reglas para el juego de 2 estados son las siguientes:
- la máquina debe tener dos estados además del estado de detención, y
- la cinta contiene inicialmente sólo ceros.
Un jugador debe concebir una tabla de transición que apunte a la salida más larga de 1 en la cinta mientras se asegura de que la máquina se detendrá eventualmente.
Un n º castor ocupado , BB- n o simplemente "castor ocupado" es una máquina de Turing que gana el n -state Busy Beaver juego. Es decir, alcanza la mayor cantidad de 1 entre todas las demás Máquinas de Turing posibles que compiten en n estados. La máquina BB-2 Turing , por ejemplo, logra cuatro 1 en seis pasos.
Determinar si una máquina de Turing arbitraria es un castor ocupado es indecidible . Esto tiene implicaciones en la teoría de la computabilidad , el problema de la detención y la teoría de la complejidad . El concepto fue introducido por primera vez por Tibor Radó en su artículo de 1962, "On Non-Computable Functions".
El juego
El n -state ocupada juego de castor (o BB- n juego ), introducido en Tibor Radó 1962 de papel 's, implica una clase de máquinas de Turing , cada miembro de que se requiere para cumplir con las siguientes especificaciones de diseño:
- La máquina tiene n estados "operativos" más un estado de detención, donde n es un número entero positivo, y uno de los n estados se distingue como el estado inicial. (Normalmente, los estados se etiquetan con 1, 2, ..., n , con el estado 1 como estado inicial, o con A , B , C , ..., con el estado A como estado inicial).
- La máquina utiliza una única cinta bidireccional infinita (o ilimitada).
- El alfabeto de la cinta es {0, 1}, con 0 como símbolo en blanco.
- La función de transición de la máquina toma dos entradas:
- el estado actual de no detención,
- el símbolo en la celda de cinta actual,
- y produce tres salidas:
- un símbolo para escribir sobre el símbolo en la celda de cinta actual (puede ser el mismo símbolo que el símbolo sobreescrito),
- una dirección para moverse (izquierda o derecha; es decir, cambiar a la celda de cinta un lugar a la izquierda o derecha de la celda actual), y
- un estado al que pasar (que puede ser el estado de detención).
- Por tanto, hay (4 n + 4) 2 n máquinas de Turing de n estados que cumplen esta definición porque la forma general de la fórmula es ( símbolos × direcciones × ( estados + 1)) ( símbolos × estados ) .
- La función de transición puede verse como una tabla finita de 5 tuplas, cada una de las cuales tiene la forma
- (estado actual, símbolo actual, símbolo a escribir, dirección de cambio, siguiente estado).
"Ejecutar" la máquina consiste en comenzar en el estado inicial, con la celda de cinta actual siendo cualquier celda de una cinta en blanco (todo-0), y luego iterar la función de transición hasta que se ingrese al estado de detención (si alguna vez). Si, y solo si, la máquina finalmente se detiene, entonces el número de unos que quedan finalmente en la cinta se denomina puntuación de la máquina .
El juego del castor ocupado de n estados (BB- n ) es un concurso para encontrar una máquina de Turing de n estados que tenga la mayor puntuación posible: el mayor número de 1 en su cinta después de detenerse. Una máquina que alcanza el puntaje más alto posible entre todas las máquinas de Turing de n estados se llama castor ocupado de n estados, y una máquina cuyo puntaje es simplemente el más alto alcanzado hasta ahora (quizás no el más grande posible) se llama campeón n- estado máquina.
Radó requirió que cada máquina inscrita en el concurso vaya acompañada de una declaración del número exacto de pasos que se necesitan para alcanzar el estado de parada, lo que permite verificar la puntuación de cada entrada (en principio) haciendo funcionar la máquina para el número indicado. de pasos. (Si las entradas consistieran solo en descripciones de máquinas, entonces el problema de verificar cada entrada potencial es indecidible, porque es equivalente al conocido problema de detención : no habría una forma efectiva de decidir si una máquina arbitraria finalmente se detiene).
Funciones relacionadas
La función del castor ocupado Σ
La función de castor ocupado cuantifica la puntuación máxima que puede alcanzar un castor ocupado en una medida determinada. Esta es una función no computable . Además, se puede demostrar que una función de castor ocupada crece asintóticamente más rápido que cualquier función computable.
La función de castor ocupado, Σ: ℕ → ℕ, se define de manera que Σ ( n ) es la puntuación máxima alcanzable (el número máximo de 1 finalmente en la cinta) entre todas las máquinas de Turing de 2 símbolos n- estados que se detienen de las anteriores- tipo descrito, cuando se inicia en una cinta en blanco.
Está claro que Σ es una función bien definida: para cada n , hay como mucho un número finito de máquinas de Turing de estado n como antes, hasta el isomorfismo, por lo tanto, como mucho, un número finito de tiempos de ejecución posibles.
Esta secuencia infinita Σ es la función de castor ocupado , y cualquier máquina M de Turing de 2 símbolos y estado n para la cual σ ( M ) = Σ ( n ) (es decir, que alcanza la puntuación máxima) se denomina castor ocupado . Tenga en cuenta que para cada n , existen al menos cuatro castores ocupados en n estados (porque, dado cualquier castor ocupado en n estados, se obtiene otro simplemente cambiando la dirección de cambio en una transición que se detiene, otro cambiando todos los cambios de dirección a su contrario , y la final cambiando la dirección de parada del atareado castor totalmente intercambiado).
No computabilidad
El artículo de Radó de 1962 demostró que si f : ℕ → ℕ es cualquier función computable , entonces Σ ( n )> f (n) para todos los n suficientemente grandes y, por lo tanto, Σ no es una función computable.
Además, esto implica que es indecidible por un algoritmo general si una máquina de Turing arbitraria es un castor ocupado. (Tal algoritmo no puede existir, porque su existencia permitiría calcular Σ, lo cual es una imposibilidad probada. En particular, dicho algoritmo podría usarse para construir otro algoritmo que calcularía Σ de la siguiente manera: para cualquier n dado , cada uno de las finitas muchas máquinas de Turing de 2 símbolos de n estados se probarían hasta que se encontrara un castor ocupado de n estados; esta máquina de castor ocupada se simularía entonces para determinar su puntuación, que es por definición Σ ( n )).
Si bien Σ ( n ) es una función no calculable, existen algunas n pequeñas para las que es posible obtener sus valores y demostrar que son correctos. No es difícil demostrar que Σ (0) = 0, Σ (1) = 1, Σ (2) = 4, y con progresivamente más dificultad se puede demostrar que Σ (3) = 6 y Σ (4) = 13 (secuencia A028444 en la OEIS ). Σ ( n ) aún no se ha determinado para ninguna instancia de n > 4, aunque se han establecido límites inferiores (consulte la sección Valores conocidos a continuación).
En 2016, Adam Yedidia y Scott Aaronson obtuvieron el primer límite superior (explícito) en el mínimo n para el cual Σ ( n ) no se puede demostrar en ZFC . Para ello, construyeron una máquina de Turing de 7910 estados cuyo comportamiento no puede probarse basándose en los axiomas habituales de la teoría de conjuntos (teoría de conjuntos de Zermelo-Fraenkel con el axioma de elección ), bajo hipótesis de consistencia razonable ( propiedad estacionaria de Ramsey ). Esto se redujo más tarde a 1919 estados, con la dependencia de la propiedad estacionaria de Ramsey eliminada, y más tarde a 748 estados.
Complejidad e imposibilidad de demostrar Σ
Una variante de la complejidad de Kolmogorov se define como sigue [cf. Boolos, Burgess & Jeffrey, 2007]: La complejidad de un número n es el número más pequeño de estados necesarios para una máquina de Turing clase BB que se detiene con un solo bloque de n 1 consecutivos en una cinta inicialmente en blanco. La variante correspondiente del teorema de incompletitud de Chaitin establece que, en el contexto de un sistema axiomático dado para los números naturales, existe un número k tal que no se puede demostrar que ningún número específico tenga una complejidad mayor que k y, por lo tanto, que ningún límite superior específico se puede probar para Σ ( k ) (lo último se debe a que "la complejidad de n es mayor que k " se probaría si se probara " n > Σ ( k )"). Como se menciona en la referencia citada, para cualquier sistema axiomático de "matemáticas ordinarias", el valor mínimo k para el cual esto es cierto es mucho menor que 10 ↑↑ 10 ; en consecuencia, en el contexto de las matemáticas ordinarias, no se puede probar ni el valor ni ningún límite superior de Σ (10 ↑↑ 10). ( El primer teorema de incompletitud de Gödel se ilustra con este resultado: en un sistema axiomático de matemáticas ordinarias, hay un enunciado verdadero pero no demostrable de la forma "Σ (10 ↑↑ 10) = n ", y hay infinitos pero-frases no demostrables de la forma "Σ (10 ↑↑ 10) < n ".)
Función de cambios máximos S
Además de la función Σ, Radó [1962] introdujo otra función extrema para la clase BB de máquinas de Turing, la función de desplazamiento máximo , S , definida de la siguiente manera:
- s ( M ) = el número de cambios que M hace antes de detenerse, para cualquier M en E n ,
- S ( n ) = máximo { s ( M ) | M ∈ E n } = el mayor número de cambios realizados por cualquier máquina de Turing de 2 símbolos de estado n que se detenga.
Debido a que se requiere que estas máquinas de Turing tengan un cambio en todas y cada una de las transiciones o "pasos" (incluida cualquier transición a un estado de detención), la función de cambios máximos es al mismo tiempo una función de pasos máximos.
Radó demostró que S no es computable por la misma razón que Σ no es computable: crece más rápido que cualquier función computable. Demostró esto simplemente señalando que para cada n , S ( n ) ≥ Σ ( n ). Cada turno puede escribir un 0 o un 1 en la cinta, mientras que Σ cuenta un subconjunto de los turnos que escribieron un 1, es decir, los que no se habían sobrescrito cuando la máquina de Turing se detuvo; en consecuencia, S crece al menos tan rápido como Σ, que ya se ha demostrado que crece más rápido que cualquier función computable.
La siguiente conexión entre Σ y S fue utilizada por Lin & Radó [ Computer Studies of Turing Machine Problems , 1965] para demostrar que Σ (3) = 6: Para un n dado , si S ( n ) es conocido, entonces todos los estados n Las máquinas de Turing pueden (en principio) funcionar hasta en S ( n ) pasos, momento en el que cualquier máquina que aún no se haya detenido nunca se detendrá. En ese punto, al observar qué máquinas se han detenido con más 1 en la cinta (es decir, los castores ocupados), se obtiene de sus cintas el valor de Σ ( n ). El enfoque utilizado por Lin & Radó para el caso de n = 3 fue conjeturar que S (3) = 21, luego simular todas las máquinas de 3 estados esencialmente diferentes para hasta 21 pasos. Al analizar el comportamiento de las máquinas que no se habían detenido en 21 pasos, lograron mostrar que ninguna de esas máquinas se detendría nunca, probando así la conjetura de que S (3) = 21, y determinando que Σ (3) = 6 por el procedimiento que se acaba de describir.
Las desigualdades que relacionan Σ y S incluyen las siguientes (de [Ben-Amram, et al., 1996]), que son válidas para todo n ≥ 1 :
y un límite mejorado asintóticamente (de [Ben-Amram, Petersen, 2002]): existe una constante c , tal que para todo n ≥ 2 ,
tiende a estar cerca del cuadrado de y, de hecho, muchas máquinas dan menos de .
Valores conocidos para Σ y S
A partir de 2016, los valores de la función para Σ ( n ) y S ( n ) solo se conocen exactamente para n <5.
El actual (a partir de 2018) campeón de castores ocupados de 5 estados produce 4098 1s, usando47 176 870 pasos (descubierto por Heiner Marxen y Jürgen Buntrock en 1989), pero sigue habiendo 18 o 19 (posiblemente bajo 10, ver más abajo) máquinas con un comportamiento no habitual que se cree que nunca se detiene, pero que no han sido probados para corre infinitamente. Skelet enumera 42 o 43 máquinas no probadas, pero 24 ya están probadas. Las máquinas restantes se han simulado en 81,8 mil millones de pasos, pero ninguna se detuvo. Daniel Briggs también probó algunas máquinas. Otra fuente dice que 98 máquinas aún no han sido probadas. Hay un análisis de los holdouts. Por lo tanto, es probable que Σ (5) = 4098 y S (5) = 47176870, pero esto no se ha probado y se desconoce si quedan reservas (a partir de 2018). Por el momento, el campeón récord de 6 estados produce más de3,515 × 10 18 267 1s (exactamente (25 × 4 30341 +23) / 9), usando más de7.412 × 10 36 534 pasos (encontrado por Pavel Kropitz en 2010). Como se señaló anteriormente, estas son máquinas de Turing de 2 símbolos.
Una simple extensión de la máquina de 6 estados conduce a una máquina de 7 estados que escribirá más de 10 10 10 1018 705 353 1 en la cinta, pero indudablemente hay máquinas de 7 estados mucho más ocupadas. Sin embargo, otros cazadores de castores ocupados tienen diferentes juegos de máquinas.
Milton Green, en su artículo de 1964 "A Lower Bound on Rado's Sigma Function for Binary Turing Machines", construyó un conjunto de máquinas de Turing que demostraban que
donde ↑ es la notación de flecha hacia arriba de Knuth y A es la función de Ackermann .
Por lo tanto
(con 3 3 3 = 7 625 597 484 987 términos en la torre exponencial), y
donde el número g 1 es el enorme valor inicial en la secuencia que define el número de Graham .
En 1964, Milton Green desarrolló un límite inferior para la función Busy Beaver que se publicó en las actas del simposio IEEE de 1964 sobre teoría de circuitos de conmutación y diseño lógico. Heiner Marxen y Jürgen Buntrock lo describieron como "un límite inferior no trivial (no primitivo recursivo)". Este límite inferior se puede calcular pero es demasiado complejo para expresarlo como una sola expresión en términos de n. Cuando n = 8, el método da Σ (8) ≥ 3 × (7 × 3 92 - 1) / 2 ≈ 8.248 × 10 44 .
Se puede derivar de los límites inferiores actuales que:
Por el contrario, el mejor límite inferior actual (a partir de 2018) en Σ (6) es 10 18 267 , que es mayor que el límite inferior dado por la fórmula de Green, 3 3 = 27 (que es pequeño en comparación). De hecho, es mucho mayor que el límite inferior: 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , que es Verde de primera límite inferior para Σ (8), y también mucho mayor que el segundo límite inferior: 3 × (7 × 3 92 -1) / 2.
Σ (7) es de la misma manera mucho, mucho mayor que el límite inferior común actual 3 31 (casi 618 billones), por lo que el segundo límite inferior también es muy, muy débil.
Prueba de incomputabilidad de S ( n ) y Σ ( n )
Suponga que S ( n ) es una función computable y deje que EvalS denote una TM, evaluando S ( n ). Dada una cinta con n 1s, producirá S ( n ) 1s en la cinta y luego se detendrá. Deje que Clean denote una máquina de Turing que limpia la secuencia de unos escritos inicialmente en la cinta. Sea Double una máquina de Turing que evalúa la función n + n . Dada una cinta con n 1s, producirá 2 n 1s en la cinta y luego se detendrá. Creemos la composición Doble | EvalS | Limpiar y dejar que n 0 sea el número de estados de esta máquina. Deje que Create_n 0 denote una máquina de Turing que crea n 0 1s en una cinta inicialmente en blanco. Esta máquina puede construirse de manera trivial para tener n 0 estados (el estado i escribe 1, mueve la cabeza hacia la derecha y cambia al estado i + 1, excepto el estado n 0 , que se detiene). Sea N la suma n 0 + n 0 .
Sea BadS la composición Create_n 0 | Doble | EvalS | Limpio . Tenga en cuenta que esta máquina tiene N estados. Comenzando con una cinta inicialmente en blanco, primero crea una secuencia de n 0 1s y luego la duplica, produciendo una secuencia de N 1s. Entonces BadS producirá S ( N ) 1 en la cinta y, por último, borrará todos los 1 y luego se detendrá. Pero la fase de limpieza continuará al menos S ( N ) pasos, por lo que el tiempo de trabajo de BadS es estrictamente mayor que S ( N ), lo que contradice la definición de la función S ( n ).
La incomputabilidad de Σ ( n ) puede demostrarse de manera similar. En la prueba anterior, se debe cambiar la máquina EvalS por EvalΣ y Limpiar con Incremento - una TM simple, buscando un primer 0 en la cinta y reemplazándolo con 1.
La incomputabilidad de S ( n ) también se puede establecer haciendo referencia al problema de detención de la cinta en blanco. El problema de la detención de la cinta en blanco es el problema de decidir para cualquier máquina de Turing si se detendrá o no cuando se encienda con una cinta vacía. El problema de detención de la cinta en blanco es equivalente al problema de detención estándar y, por lo tanto, también es incuestionable. Si S ( n ) fuera computable, entonces podríamos resolver el problema de detención de la cinta en blanco simplemente ejecutando cualquier máquina de Turing dada con n estados para S ( n ) pasos; si todavía no se ha detenido, nunca lo hará. Por lo tanto, dado que el problema de detención de la cinta en blanco no es computable, se deduce que S ( n ) debe ser igualmente incomputable.
Generalizaciones
Para cualquier modelo de cálculo existen análogos simples del castor ocupado. Por ejemplo, la generalización a las máquinas de Turing con n estados y m símbolos define las siguientes funciones generalizadas de castor ocupado :
- Σ ( n , m ): el mayor número de no ceros imprimibles por un estado n , máquina de símbolo m que se inició en una cinta inicialmente en blanco antes de detenerse, y
- S ( n , m ): el mayor número de pasos dados por una máquina de n- estado, símbolo m , iniciada en una cinta inicialmente en blanco antes de detenerse.
Por ejemplo, la máquina de 3 símbolos de 3 estados más antigua encontrada hasta ahora ejecuta 119 112 334 170 342 540 pasos antes de detenerse. La máquina de 2 símbolos y 6 estados de funcionamiento más prolongado que tiene la propiedad adicional de invertir el valor de la cinta en cada paso produce6147 1 s después47 339 970 pasos. Entonces S RTM (6) ≥47 339 970 y Σ RTM (6) ≥6147 .
Es posible generalizar aún más la función de castor ocupado extendiéndola a más de una dimensión.
Asimismo, podríamos definir una función análoga a la Σ para máquinas de registro como el número más grande que puede estar presente en cualquier registro al detenerse, para un número dado de instrucciones.
Valores exactos y límites inferiores
La siguiente tabla enumera los valores exactos y algunos límites inferiores conocidos para S ( n , m ) y Σ ( n , m ) para los problemas generalizados de castores ocupados. Nota: entradas enumeradas como "?" están delimitados desde abajo por el máximo de todas las entradas a la izquierda y arriba. Estas máquinas no han sido investigadas o fueron posteriormente superadas por una máquina más pequeña.
Las máquinas de Turing que alcanzan estos valores están disponibles en la página web de Pascal Michel . Cada uno de estos sitios web también contiene algún análisis de las máquinas de Turing y referencias a las pruebas de los valores exactos.
Valores de S ( n , m ) nortemetro2 estados 3 estados 4 estados 5 estados 6 estados 7 estados 2 símbolos 6 21 107 47 176 870 ? > 7,4 × 10 36 534 > 10 10 10 1018 705 353 3-símbolo 38 ≥ 119 112 334 170 342 540 > 1,0 × 10 14 072 ? ? ? 4 símbolos ≥ 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5-símbolo > 1,9 × 10 704 ? ? ? ? ? 6-símbolo > 2,4 × 10 9866 ? ? ? ? ? Valores de Σ ( n , m ) nortemetro2 estados 3 estados 4 estados 5 estados 6 estados 7 estados 2 símbolos 4 6 13 4098 ? > 3,5 × 10 18 267 > 10 10 10 1018 705 353 3-símbolo 9 ≥ 374 676 383 > 1,3 × 10 7036 ? ? ? 4 símbolos ≥ 2050 > 3,7 × 10 6518 ? ? ? ? 5-símbolo > 1,7 × 10 352 ? ? ? ? ? 6-símbolo > 1,9 × 10 4933 ? ? ? ? ?
Máquinas de Turing no deterministas
| pag | pasos | estados |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
El problema se puede extender a las máquinas de Turing no deterministas buscando el sistema con la mayor cantidad de estados en todas las ramas o la rama con la mayor cantidad de pasos. La cuestión de si un NDTM dado se detendrá sigue siendo computacionalmente irreducible, y el cálculo requerido para encontrar un castor ocupado con NDTM es significativamente mayor que en el caso determinista, ya que hay múltiples ramas que deben tenerse en cuenta. Para un sistema de 2 estados y 2 colores con p casos o reglas, la tabla de la derecha proporciona el número máximo de pasos antes de detenerse y el número máximo de estados únicos creados por el NDTM.
Aplicaciones
Además de plantear un juego matemático bastante desafiante , las ocupadas funciones Beaver ofrecen un enfoque completamente nuevo para resolver problemas de matemáticas puras. Muchos problemas abiertos en matemáticas podrían resolverse en teoría, pero no en la práctica, de manera sistemática dado el valor de S ( n ) para una n suficientemente grande .
Considere cualquier conjetura que pueda refutarse mediante un contraejemplo entre un número contable de casos (por ejemplo, la conjetura de Goldbach ). Escriba un programa de computadora que compruebe secuencialmente esta conjetura en busca de valores crecientes. En el caso de la conjetura de Goldbach, consideraríamos cada número par ≥ 4 secuencialmente y probaríamos si es o no la suma de dos números primos. Suponga que este programa se simula en una máquina de Turing de n estados. Si encuentra un contraejemplo (un número par ≥ 4 que no es la suma de dos primos en nuestro ejemplo), se detiene e indica eso. Sin embargo, si la conjetura es cierta, nuestro programa nunca se detendrá. (Este programa se detiene solo si encuentra un contraejemplo).
Ahora, este programa es simulado por una máquina de Turing de n estados, por lo que si conocemos S ( n ) podemos decidir (en una cantidad finita de tiempo) si se detendrá o no simplemente ejecutando la máquina tantos pasos. Y si, después de S ( n ) pasos, la máquina no se detiene, sabemos que nunca lo hará y, por lo tanto, no hay contraejemplos para la conjetura dada (es decir, no hay números pares que no sean la suma de dos primos). Esto probaría que la conjetura es cierta.
Por lo tanto, los valores específicos (o límites superiores) para S ( n ) podrían usarse para resolver sistemáticamente muchos problemas abiertos en matemáticas (en teoría). Sin embargo, los resultados actuales sobre el problema del castor ocupado sugieren que esto no será práctico por dos razones:
- Es extremadamente difícil probar los valores para la función de castor ocupado (y la función de cambio máximo). Solo se ha probado para máquinas extremadamente pequeñas con menos de cinco estados, mientras que presumiblemente se necesitarían al menos 20-50 estados para hacer una máquina útil. Además, cada valor exacto conocido de S ( n ) fue probado enumerando cada máquina de Turing de n estados y probando si cada una se detiene o no. Habría que calcular S ( n ) por algún método menos directo para que sea realmente útil.
- Pero incluso si uno encontrara una mejor manera de calcular S ( n ), los valores de la función de castor ocupado (y la función de cambio máximo) se vuelven muy grandes, muy rápido. S (6)> 1036 534 ya requiere una aceleración especial basada en patrones para poder simular hasta su finalización. Del mismo modo, sabemos que S (10)> Σ (10)> 3 ↑↑↑ 3 es un número gigantesco y S (17)> Σ (17)> G, donde G es el número de Graham, un número enorme. Por lo tanto, incluso si supiéramos, digamos, S (30), es completamente irrazonable ejecutar cualquier máquina ese número de pasos. No hay suficiente capacidad computacional en la parte conocida del universo para haber realizado inclusooperaciones S (6) directamente.
Instancias notables
Se ha construido una máquina de Turing binaria de 748 estados que se detiene si ZFC es inconsistente. Se ha construido una máquina de Turing de 744 estados que se detiene si la hipótesis de Riemann es falsa. Se ha construido una máquina de Turing de 43 estados que se detiene si la conjetura de Goldbach es falsa, y se ha propuesto una máquina de 27 estados para esa conjetura, pero aún no se ha verificado.
Se ha construido una máquina de Turing de 15 estados que se detiene si la siguiente conjetura formulada por Paul Erdős en 1979 es falsa: para todo n> 8 hay al menos un dígito 2 en la representación de base 3 de 2 n .
Ejemplos de
Estas son tablas de reglas para las máquinas de Turing que generan Σ (1) y S (1), Σ (2) y S (2), Σ (3) (pero no S (3)), Σ (4) y S (4) y el límite inferior más conocido para Σ (5) y S (5), y Σ (6) y S (6). Para otras visualizaciones,
En las tablas, las columnas representan el estado actual y las filas representan el símbolo actual leído de la cinta. Cada entrada de la tabla es una cadena de tres caracteres, que indica el símbolo a escribir en la cinta, la dirección para moverse y el nuevo estado (en ese orden). El estado de detención se muestra como H .
Cada máquina comienza en el estado A con una cinta infinita que contiene todos los ceros. Por tanto, el símbolo inicial leído de la cinta es un 0.
Resultado clave: (comienza en la posición overlined , detenida en la posición subrayados )
Castor ocupado de 1 estado y 2 símbolos A 0 1R H 1 (no utilizado)
Resultado: 0 0 1 0 0 (1 paso, un "1" en total)
Castor ocupado de 2 estados y 2 símbolos A B 0 1R B 1L A 1 1L B 1R H
Resultado: 0 0 1 1 1 1 0 0 (6 pasos, cuatro "1" en total)
Castor ocupado de 3 estados y 2 símbolos A B C 0 1R B 0R C 1L C 1 1R H 1R B 1L A
Resultado: 0 0 1 1 1 1 1 1 0 0 (14 pasos, seis "1" en total).
A diferencia de las máquinas anteriores, éste es un castor ocupado sólo por Σ, pero no para S . ( S (3) = 21.)
Castor ocupado de 4 estados y 2 símbolos A B C D 0 1R B 1L A 1R H 1R D 1 1L B 0L C 1L D 0R A
Resultado: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 pasos, trece "1" en total)
Mejor contendiente actual de 5 estados y 2 símbolos (posible castor ocupado) A B C D mi 0 1R B 1R C 1R D 1L A 1R H 1 1L C 1R B 0L E 1L D 0L A
Resultado: 4098 "1" s con 8191 "0" s intercalados en 47,176,870 pasos.
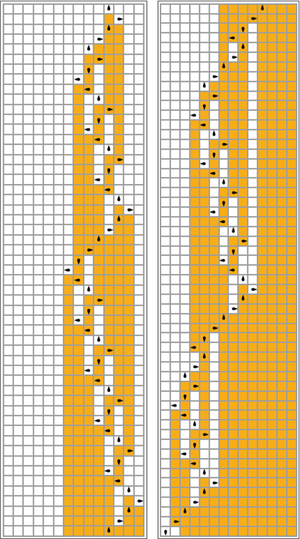
Observe en la imagen de la derecha cómo esta solución es cualitativamente similar a la evolución de algunos autómatas celulares .
Mejor contendiente actual de 6 estados y 2 símbolos A B C D mi F 0 1R B 1R C 1L D 1R E 1L A 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
Resultado: ≈3,515 × 10 18267 "1" s en ≈7,412 × 10 36534 pasos.
Visualizaciones
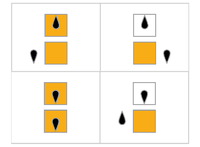
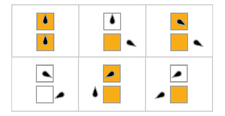
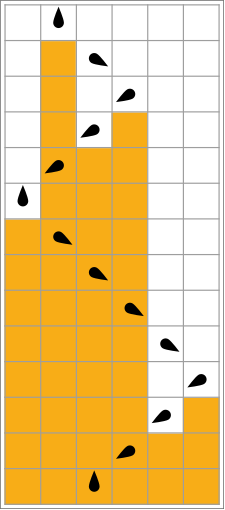
En la siguiente tabla, las reglas para cada castor ocupado (maximizando Σ) se representan visualmente, con cuadrados naranjas correspondientes a un "1" en la cinta, y blancos correspondientes a "0". La posición de la cabeza está indicada por el ovoide negro, y la orientación de la cabeza representa el estado. Las cintas individuales se colocan horizontalmente, con el tiempo progresando verticalmente. El estado de detención está representado por una regla que asigna un estado a sí mismo (la cabeza no se mueve).
Ver también
Notas
- ↑ a b Radó, Tibor (mayo de 1962). "Sobre funciones no computables" (PDF) . Revista técnica de Bell System . 41 (3): 877–884. doi : 10.1002 / j.1538-7305.1962.tb00480.x .
- ^ Chaitin (1987)
- ^ Adam Yedidia y Scott Aaronson (mayo de 2016). Una máquina de Turing relativamente pequeña cuyo comportamiento es independiente de la teoría de conjuntos (Informe técnico). MIT. arXiv : 1605.04343 . Código bibliográfico : 2016arXiv160504343Y .
- ^ Aron, Jacob. "Esta máquina de Turing debería funcionar para siempre a menos que las matemáticas estén mal" . Consultado el 25 de septiembre de 2016 .
- ^ a b La versión del 3 de mayo contenía 7918 estados: "El número 8000th Busy Beaver elude la teoría de conjuntos ZF" . Blog optimizado para Shtetl . 2016-05-03 . Consultado el 25 de septiembre de 2016 .
- ^ a b c "Tres anuncios" . Blog optimizado para Shtetl . 2016-05-03 . Consultado el 27 de abril de 2018 .
- ^ "GitHub - sorear / metamath-turing-machines: enumeradores a prueba de Metamath y otras cosas" . 2019-02-13.
- ^ "La frontera de los castores ocupados" (PDF) .
- ^ "Página de Skelet para el problema de Busy Beaver" . skelet.ludost.net .
- ^ Turing: un proyecto para terminar Busy Beaver de 5
- ^ "El problema del castor ocupado: un nuevo ataque del milenio" .
- ↑ a b Wolfram, Stephen (4 de febrero de 2021). "Máquinas de Turing de múltiples vías" . www.wolframphysics.org .
- ^ Chaitin 1987
- ^ Lloyd 2001. Capacidad computacional del universo .
- ↑ a b c Pavlus, John (10 de diciembre de 2020). "Cómo los programas informáticos más lentos iluminan los límites fundamentales de las matemáticas" . Revista Quanta . Consultado el 11 de diciembre de 2020 .
- ^ Tristan Stérin y Damien Woods (julio de 2021). Sobre la dureza de conocer los valores de los castores ocupados BB (15) y BB (5,4) (Informe técnico). Universidad de Maynooth. arXiv : 2107.12475 .
- ^ Erdõs, Paul (1979). "Algunos problemas no convencionales en teoría de números" . Matemáticas. revista 52 (2): 67–70. doi : 10.1080 / 0025570X.1979.11976756 .
- ^ Lin, Shen; Rado, Tibor (abril de 1965). "Estudios informáticos de problemas de la máquina de Turing" . Revista de la ACM . 12 (2): 196–212. doi : 10.1145 / 321264.321270 . S2CID 17789208 .
Referencias
-
Radó, Tibor (mayo de 1962). "Sobre funciones no computables" (PDF) . Revista técnica de Bell System . 41 (3): 877–884. doi : 10.1002 / j.1538-7305.1962.tb00480.x .
- Aquí es donde Radó definió por primera vez el problema de los castores ocupados y demostró que era incuestionable y crecía más rápido que cualquier función computable.
-
Lin, Shen; Radó, Tibor (abril de 1965). "Estudios informáticos de problemas de la máquina de Turing" . Revista de la ACM . 12 (2): 196–212. doi : 10.1145 / 321264.321270 . S2CID 17789208 .
- Los resultados de este artículo ya habían aparecido en parte en la tesis doctoral de Lin de 1963, bajo la dirección de Radó. Lin y Radó prueban que Σ (3) = 6 y S (3) = 21 al demostrar que todas las Máquinas de Turing de 3 estados y 2 símbolos que no se detienen en 21 pasos nunca se detendrán. (La mayoría se prueban automáticamente mediante un programa de computadora, sin embargo, 40 se prueban mediante inspección humana).
-
Brady, Allen H. (abril de 1983). "La determinación del valor de la función no computable de Rado Σ ( k ) para máquinas de Turing de cuatro estados" . Matemáticas de la Computación . 40 (162): 647–665. doi : 10.1090 / S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Brady demuestra que Σ (4) = 13 y S (4) = 107. Brady define dos nuevas categorías para las Máquinas de Turing de 3 estados y 2 símbolos que no se detienen: árboles de Navidad y contadores. Él usa un programa de computadora para demostrar que todas las máquinas excepto 27 que ejecutan 107 pasos son variantes de árboles de Navidad y contadores que se puede probar que funcionan infinitamente. Las últimas 27 máquinas (denominadas holdouts) han sido probadas por inspección personal por el propio Brady para no detenerse.
-
Machlin, Rona; Stout, Quentin F. (junio de 1990). "El comportamiento complejo de las máquinas simples" . Physica D: Fenómenos no lineales . 42 (1–3): 85–98. Código Bibliográfico : 1990PhyD ... 42 ... 85M . doi : 10.1016 / 0167-2789 (90) 90068-Z . hdl : 2027,42 / 28528 .
- Machlin y Stout describen el problema de los castores ocupados y muchas técnicas utilizadas para encontrar castores ocupados (que aplican a las Máquinas de Turing con 4 estados y 2 símbolos, verificando así la prueba de Brady). Sugieren cómo estimar una variante de la probabilidad de detención de Chaitin (Ω).
-
Marxen, Heiner; Buntrock, Jürgen (febrero de 1990). "Atacando al Busy Beaver 5" . Boletín de la EATCS . 40 : 247-251. Archivado desde el original el 9 de octubre de 2006 . Consultado el 19 de enero de 2020 .
- Marxen y Buntrock demuestran que Σ (5) ≥ 4098 y S (5) ≥ 47 176 870 y describen en detalle el método que utilizaron para encontrar estas máquinas y demostrar que muchas otras nunca se detendrán.
-
Green, Milton W. (1964). Un límite inferior en la función Sigma de Rado para máquinas de Turing binarias . 1964 Actas del Quinto Simposio Anual sobre Teoría de Circuitos de Conmutación y Diseño Lógico . págs. 91–94. doi : 10.1109 / SWCT.1964.3 .
- Green construye máquinas de forma recursiva para cualquier número de estados y proporciona la función recursiva que calcula su puntuación (calcula σ), proporcionando así un límite inferior para Σ. El crecimiento de esta función es comparable al de la función de Ackermann .
-
Dewdney, Alexander K. (1984). "Una trampa de computadora para el castor ocupado, la máquina de Turing más trabajadora". Scientific American . 251 (2): 10–17.
- Alexander Dewdney describe los programas de los castores ocupados en Scientific American , agosto de 1984, páginas 19–23, también marzo de 1985, p. 23 y abril de 1985 p. 30 .
- Chaitin, Gregory J. (1987). "Computación de la función Busy Beaver" (PDF) . En Portada, TM; Gopinath, B. (eds.). Problemas abiertos en comunicación y computación . Saltador. págs. 108–112. ISBN 978-0-387-96621-2.
-
Brady, Allen H. (1995). "El juego del castor ocupado y el significado de la vida". En Herken, Rolf (ed.). La máquina universal de Turing: una encuesta de medio siglo (2ª ed.). Viena, Nueva York: Springer-Verlag. págs. 237-254. ISBN 978-3-211-82637-9.
- Donde Brady (de fama de 4 estados) describe algo de la historia de la bestia y llama a su búsqueda "El juego del castor ocupado". Describe otros juegos (por ejemplo, autómatas celulares y Game of Life de Conway ). De particular interés es "El juego del castor ocupado en dos dimensiones" (p. 247). Con 19 referencias.
-
Booth, Taylor L. (1967). Máquinas secuenciales y teoría de los autómatas . Nueva York: Wiley. ISBN 978-0-471-08848-6.
- Cfr. Capítulo 9, Máquinas de Turing. Un libro difícil, destinado a ingenieros eléctricos y especialistas técnicos. Discute la recursividad, recursividad parcial con referencia a las máquinas de Turing, problema de detención. Una referencia en Booth atribuye a Rado un castor ocupado. Booth también define el problema de los castores ocupados de Rado en "problemas domésticos" 3, 4, 5, 6 del Capítulo 9, p. 396. El problema 3 es "mostrar que el problema del castor ocupado no tiene solución ... para todos los valores de n".
-
Ben-Amram, AM; Julstrom, BA; Zwick, U. (1996). "Una nota sobre los castores ocupados y otras criaturas" . Teoría de sistemas matemáticos . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007 / BF01192693 . S2CID 30937913 .
- Límites entre las funciones Σ y S .
-
Ben-Amram, AM; Petersen, H. (2002). "Límites mejorados para funciones relacionadas con los castores ocupados". Teoría de los sistemas informáticos . 35 : 1-11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007 / s00224-001-1052-0 . S2CID 10429773 .
- Límites mejorados.
-
Lafitte, G .; Papazian, C. (junio de 2007). "El tejido de las pequeñas máquinas de Turing". Computación y lógica en el mundo real, Actas de la Tercera Conferencia sobre Computabilidad en Europa . págs. 219-227. CiteSeerX 10.1.1.104.3021 .
- Este artículo contiene una clasificación completa de las máquinas de Turing de 2 estados y 3 símbolos y, por lo tanto, una prueba del castor ocupado (2, 3): Σ (2, 3) = 9 y S (2, 3) = 38.
- Boolos, George S .; Burgess, John P .; Jeffrey, Richard C. (2007). Computabilidad y lógica (Quinta ed.). Prensa de la Universidad de Cambridge. ISBN 978-0-521-87752-7.
-
Kropitz, Pavel (2010). Problém Busy Beaver (tesis de licenciatura) (en eslovaco). Universidad Charles de Praga.
- Esta es la descripción de las ideas, de los algoritmos y su implementación, con la descripción de los experimentos que examinan máquinas de Turing de 5 y 6 estados mediante ejecución en paralelo en 31 computadoras de 4 núcleos y, finalmente, los mejores resultados para la TM de 6 estados.
enlaces externos
- La página de Heiner Marxen , quien, con Jürgen Buntrock, encontró los registros antes mencionados para una máquina de Turing de 5 y 6 estados.
- Estudio histórico de Pascal Michel sobre los resultados de los castores ocupados, que también contiene los mejores resultados y algunos análisis.
- Definición de la clase RTM - Reversal Turing Machines, subclase simple y fuerte de las TM.
- El " Ataque del Milenio " en el Laboratorio RAIR de Rensselaer sobre el ajetreado problema de los castores. Este esfuerzo encontró varios registros nuevos y estableció varios valores para la formalización cuádruple.
- Archivo y foro del sitio web de Daniel Briggs para resolver el problema del castor ocupado de 5 estados y 2 símbolos, según la lista de máquinas no regulares de Skelet (Georgi Georgiev).
- Aaronson, Scott (1999), ¿Quién puede nombrar el número más grande?
- Weisstein, Eric W. "Busy Beaver" . MathWorld .
- Busy Beaver Turing Machines - Computerphile
- Pascal Michel. La competencia Busy Beaver: un estudio histórico . 70 páginas. 2017. <hal-00396880v5>