Ábaco Abacus

El ábaco ( plural ábacos o ábacos ), también llamado un marco de cuenta , es una herramienta de cálculo que se ha utilizado desde tiempos antiguos . Se usó en el antiguo Cercano Oriente , Europa , China y Rusia , siglos antes de la adopción del sistema de numeración arábiga . El origen exacto del ábaco aún no se ha descubierto. Consiste en hileras de cuentas móviles u objetos similares, ensartados en un alambre. Representan dígitos. Se configura uno de los dos números y las cuentas se manipulan para realizar una operación como la suma, o incluso una raíz cuadrada o cúbica.
En sus primeros diseños, las filas de cuentas podían estar sueltas sobre una superficie plana o deslizarse en ranuras. Más tarde, las cuentas se hicieron deslizar sobre varillas y se construyeron en un marco, lo que permitió una manipulación más rápida. Los ábacos todavía se fabrican, a menudo como un marco de bambú con cuentas que se deslizan sobre cables. En el mundo antiguo, particularmente antes de la introducción de la notación posicional , los ábacos eran una herramienta práctica de cálculo. El ábaco todavía se usa para enseñar los fundamentos de las matemáticas a algunos niños, por ejemplo, en los estados postsoviéticos .
Se han utilizado diseños como el soroban japonés para cálculos prácticos de números de hasta varios dígitos. Cualquier diseño de ábaco en particular admite múltiples métodos para realizar cálculos, incluidas las cuatro operaciones básicas y las raíces cuadradas y cúbicas . Algunos de estos métodos funcionan con números no naturales (números como 1,5 y 3 ⁄ 4 ).
Aunque hoy en día se utilizan comúnmente calculadoras y computadoras en lugar de ábacos, los ábacos siguen siendo de uso diario en algunos países. Los comerciantes, comerciantes y empleados en algunas partes de Europa del Este , Rusia , China y África usan ábaco. El ábaco sigue siendo de uso común como sistema de puntuación en juegos de mesa no electrónicos. Otros pueden usar un ábaco debido a una discapacidad visual que impide el uso de una calculadora.
Etimología
La palabra ábaco se remonta al menos a 1387 d.C., cuando una obra en inglés medio tomó prestada la palabra del latín que describía un ábaco de arena. La palabra latina se deriva del griego antiguo ἄβαξ ( abax ) que significa algo sin base, y coloquialmente, cualquier pieza de material rectangular. Alternativamente, sin hacer referencia a textos antiguos sobre etimología, se ha sugerido que significa "una tablilla cuadrada cubierta de polvo", o "tablero de dibujo cubierto de polvo (para el uso de las matemáticas)" (la forma exacta del latín quizás refleja el genitivo de la palabra griega, ἄβακoς ( Abakos ). Mientras que la mesa llena con la definición de polvo es muy popular, hay quienes sostienen la evidencia es insuficiente para esa conclusión. griega ἄβαξ probablemente tomado de una lengua semítica del noroeste como fenicia , evidenciado por un cognado con la palabra hebrea ʾābāq ( אבק ), o "polvo" (en el sentido posbíblico "arena usada como superficie para escribir").
Ambos ábacos y abaci (blando o duro "c") se utilizan como plurales. El usuario de un ábaco se llama abacista .
Historia
Mesopotamia
El ábaco sumerio apareció entre el 2700 y el 2300 a. C. Tenía una tabla de columnas sucesivas que delimitaban los sucesivos órdenes de magnitud de su sistema numérico sexagesimal (base 60).
Algunos eruditos señalan un carácter en cuneiforme babilónico que puede haber sido derivado de una representación del ábaco. Es la creencia de los eruditos del Antiguo Babilónico, como Ettore Carruccio, que los Antiguos Babilonios "pueden haber usado el ábaco para las operaciones de suma y resta; sin embargo, este dispositivo primitivo resultó difícil de usar para cálculos más complejos".
Egipto
El historiador griego Herodoto mencionó el ábaco en el Antiguo Egipto . Escribió que los egipcios manipulaban los guijarros de derecha a izquierda, en dirección opuesta al método griego de izquierda a derecha. Los arqueólogos han encontrado discos antiguos de varios tamaños que se cree que se utilizaron como contadores. Sin embargo, aún no se han descubierto las representaciones de este instrumento en las paredes.
Persia
Alrededor del 600 a. C., los persas comenzaron a usar el ábaco durante el Imperio aqueménida . Bajo los imperios parto , sasánida e iraní , los académicos se concentraron en intercambiar conocimientos e invenciones con los países que los rodeaban ( India , China y el Imperio Romano) , que es la forma en que el ábaco puede haber sido exportado a otros países.
Grecia
La evidencia arqueológica más temprana del uso del ábaco griego data del siglo V a. C. Demóstenes (384 a. C.-322 a. C.) se quejó de que la necesidad de utilizar guijarros para los cálculos era demasiado difícil. Una obra de Alexis del siglo IV a. C. menciona un ábaco y guijarros para la contabilidad, y tanto Diógenes como Polibio utilizan el ábaco como metáfora del comportamiento humano, afirmando "que los hombres que a veces representaban más y otras menos" como los guijarros de un ábaco. El ábaco griego era una mesa de madera o mármol, preestablecida con pequeños contadores de madera o metal para cálculos matemáticos. Este ábaco griego se utilizó en la Persia aqueménida, la civilización etrusca , la antigua Roma y el mundo cristiano occidental hasta la Revolución Francesa .
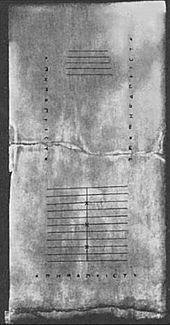
Una tablilla encontrada en la isla griega de Salamina en 1846 d.C. (la tablilla de Salamina ) data del 300 a.C., lo que la convierte en la tabla de conteo más antigua descubierta hasta ahora. Es una losa de mármol blanco de 149 cm (59 pulgadas) de largo, 75 cm (30 pulgadas) de ancho y 4,5 cm (2 pulgadas) de espesor, en la que hay 5 grupos de marcas. En el centro de la tableta hay un conjunto de 5 líneas paralelas divididas igualmente por una línea vertical, rematadas con un semicírculo en la intersección de la línea horizontal más inferior y la línea vertical única. Debajo de estas líneas hay un espacio amplio con una grieta horizontal que lo divide. Debajo de esta grieta hay otro grupo de once líneas paralelas, nuevamente divididas en dos secciones por una línea perpendicular a ellas, pero con el semicírculo en la parte superior de la intersección; la tercera, sexta y novena de estas líneas están marcadas con una cruz donde se cruzan con la línea vertical. También de este período de tiempo, el Vaso Darius fue desenterrado en 1851. Estaba cubierto de imágenes, incluido un "tesorero" que sostenía una tableta de cera en una mano mientras manipulaba los contadores de una mesa con la otra.
porcelana

| Ábaco | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chino tradicional | 算盤 | ||||||||||||||||||||||
| Chino simplificado | 算盘 | ||||||||||||||||||||||
| Significado literal | "bandeja de cálculo" | ||||||||||||||||||||||
| |||||||||||||||||||||||
La documentación escrita más antigua conocida del ábaco chino data del siglo II a. C.
El ábaco chino, también conocido como suanpan (算盤 / 算盘, literalmente "bandeja de cálculo"), mide típicamente 20 cm (8 pulgadas) de alto y viene en varios anchos, dependiendo del operador. Suele tener más de siete varillas. Hay dos cuentas en cada varilla en la cubierta superior y cinco cuentas en la inferior. Las cuentas suelen ser redondeadas y de madera dura . Las cuentas se cuentan moviéndolas hacia arriba o hacia abajo hacia la viga; las cuentas que se mueven hacia la viga se cuentan, mientras que las que se alejan de ella no. Una de las cuentas superiores es 5, mientras que una de las inferiores es 1. Cada varilla tiene un número debajo, que muestra el valor posicional. El suanpan se puede restablecer a la posición inicial instantáneamente mediante un movimiento rápido a lo largo del eje horizontal para hacer girar todas las cuentas lejos de la viga horizontal en el centro.
El prototipo del ábaco chino apareció durante la dinastía Han , y las cuentas son ovaladas. La dinastía Song y antes usaban el tipo 1: 4 o ábaco de cuatro cuentas similar al ábaco moderno, incluida la forma de las cuentas comúnmente conocidas como ábaco de estilo japonés.
A principios de la dinastía Ming , el ábaco comenzó a aparecer en una proporción de 1: 5. La cubierta superior tenía una cuenta y la inferior tenía cinco cuentas. A finales de la dinastía Ming, los estilos de ábaco aparecieron en una proporción de 2: 5. La cubierta superior tenía dos cuentas y la inferior cinco.
Se idearon varias técnicas de cálculo para Suanpan que permiten cálculos eficientes. Algunas escuelas enseñan a los estudiantes cómo usarlo.
En el largo pergamino A lo largo del río Durante el Festival Qingming pintado por Zhang Zeduan durante la dinastía Song (960-1297), un suanpan es claramente visible junto a un libro de cuentas y recetas médicas en el mostrador de un boticario (Feibao).
La similitud del ábaco romano con el chino sugiere que uno podría haber inspirado al otro, dada la evidencia de una relación comercial entre el Imperio Romano y China. Sin embargo, no se ha demostrado una conexión directa, y la similitud de los ábacos puede ser una coincidencia, ya que ambos surgen en última instancia de contar con cinco dedos por mano. Donde el modelo romano (como la mayoría de los coreanos y japoneses modernos ) tiene 4 más 1 cuenta por lugar decimal, el suanpan estándar tiene 5 más 2. Por cierto, esto permite su uso con un sistema numérico hexadecimal (o cualquier base hasta 18) que puede tener Se ha utilizado para las medidas de peso tradicionales chinas. (En lugar de funcionar con cables como en los modelos chino, coreano y japonés, el modelo romano usó ranuras, presumiblemente haciendo los cálculos aritméticos mucho más lentos).
Otra posible fuente del suanpan son las varillas de conteo chinas , que funcionaban con un sistema decimal pero carecían del concepto de cero como marcador de posición. El cero probablemente se introdujo a los chinos en la dinastía Tang (618-907) cuando viajar por el Océano Índico y el Medio Oriente les habría proporcionado un contacto directo con India , lo que les permitió adquirir el concepto de cero y el punto decimal de los comerciantes indios. y matemáticos.
Roma

El método normal de cálculo en la antigua Roma, como en Grecia, era mover contadores sobre una mesa lisa. Originalmente se usaban guijarros ( cálculos ). Posteriormente, y en la Europa medieval, se fabricaron jetons . Las líneas marcadas indicaban unidades, cinco, diez, etc., como en el sistema de números romanos . Este sistema de "contracasting" continuó en el Imperio Romano tardío y en la Europa medieval y persistió en un uso limitado hasta el siglo XIX. Debido a la reintroducción del ábaco por el Papa Silvestre II con modificaciones, volvió a ser ampliamente utilizado en Europa durante el siglo XI. movido más fácilmente.
Escribiendo en el siglo I a.C., Horacio se refiere al ábaco de cera, un tablero cubierto con una fina capa de cera negra en la que se inscribieron columnas y figuras con un lápiz.
Un ejemplo de evidencia arqueológica del ábaco romano , que se muestra cerca en una reconstrucción, data del siglo I d.C. Tiene ocho ranuras largas que contienen hasta cinco cuentas en cada una y ocho ranuras más cortas que tienen una o ninguna cuenta en cada una. La ranura marcada con I indica unidades, X decenas y así sucesivamente hasta millones. Las cuentas en las ranuras más cortas denotan cinco, cinco unidades, cinco decenas, etc., esencialmente en un sistema decimal codificado bi-quinario , relacionado con los números romanos . Es posible que las ranuras cortas de la derecha se hayan utilizado para marcar "onzas" romanas (es decir, fracciones).
India
El Abhidharmakośabhāṣya de Vasubandhu (316-396), una obra sánscrita sobre filosofía budista , dice que el filósofo Vasumitra del siglo II d.C. dijo que "colocar una mecha (sánscrito vartikā ) en el número uno ( ekāṅka ) significa que es uno mientras se coloca la mecha en el número cien significa que se llama cien, y en el número mil significa que es mil ". No está claro exactamente cuál pudo haber sido este arreglo. Alrededor del siglo V, los escribanos indios ya estaban encontrando nuevas formas de registrar el contenido del ábaco. Los textos hindúes utilizaron el término śūnya (cero) para indicar la columna vacía en el ábaco.
Japón
En Japón, el ábaco se llama soroban (算盤, そ ろ ば ん, lit. "bandeja de conteo"). Fue importado de China en el siglo XIV. Probablemente estaba en uso por la clase trabajadora un siglo o más antes de que la clase dominante lo adoptara, ya que la estructura de clases obstruía tales cambios. El ábaco 1: 4, que elimina la segunda y la quinta cuenta, que rara vez se usan, se hizo popular en la década de 1940.
El ábaco japonés de hoy es un ábaco de cuatro cuentas de tipo 1: 4, introducido desde China en la era Muromachi . Adopta la forma de la cubierta superior una cuenta y la inferior cuatro cuentas. La cuenta superior en la cubierta superior era igual a cinco y la inferior es similar al ábaco chino o coreano, y el número decimal se puede expresar, por lo que el ábaco está diseñado como un dispositivo de uno: cuatro. Las cuentas siempre tienen forma de diamante. Por lo general, se utiliza la división del cociente en lugar del método de división; al mismo tiempo, para hacer que los dígitos de la multiplicación y la división utilicen consistentemente la multiplicación de la división. Más tarde, Japón tuvo un ábaco 3: 5 llamado 天 三 算盤, que ahora se encuentra en la colección Ize Rongji de Shansi Village en la ciudad de Yamagata . Japón también usó un ábaco tipo 2: 5.
El ábaco de cuatro cuentas se extendió y se volvió común en todo el mundo. Las mejoras al ábaco japonés surgieron en varios lugares. En China se utilizó un ábaco de cuentas de plástico con estructura de aluminio. La lima está al lado de las cuatro cuentas, y presionando el botón de "limpieza" coloque la cuenta superior en la posición superior y la cuenta inferior en la posición inferior.
El ábaco todavía se fabrica en Japón incluso con la proliferación, practicidad y asequibilidad de las calculadoras electrónicas de bolsillo . El uso del soroban todavía se enseña en las escuelas primarias japonesas como parte de las matemáticas , principalmente como una ayuda para un cálculo mental más rápido. El uso de imágenes visuales puede completar un cálculo tan rápido como un instrumento físico.
Corea
El ábaco chino emigró de China a Corea alrededor del 1400 d.C. Los coreanos lo llaman jupan ( 주판 ), supan (수판) o jusan (주산). El ábaco de cuatro cuentas (1: 4) se introdujo durante la dinastía Goryeo . El ábaco 5: 1 se introdujo en Corea desde China durante la dinastía Ming.
América nativa

Algunas fuentes mencionan el uso de un ábaco llamado nepohualtzintzin en la antigua cultura azteca . Este ábaco mesoamericano utilizó un sistema de base 20 de 5 dígitos. La palabra Nepōhualtzintzin[nepoːwaɬˈt͡sint͡sin] proviene del náhuatl , formado por las raíces; Ne - personal -; pōhual o pōhualli [ˈPoːwalːi] - la cuenta -; y tzintzin [ˈT͡sint͡sin] - pequeños elementos similares. Su significado completo se tomó como: contar con pequeños elementos similares. Su uso fue enseñado en el Calmecac al temalpouhqueh [temaɬˈpoʍkeʔ] , quienes fueron estudiantes dedicados a tomar las cuentas de los cielos, desde la infancia.
El Nepōhualtzintzin se dividió en dos partes principales separadas por una barra o cordón intermedio. En la parte izquierda había cuatro cuentas. Las cuentas de la primera fila tienen valores unitarios (1, 2, 3 y 4), y en el lado derecho, tres cuentas tienen valores de 5, 10 y 15, respectivamente. Para conocer el valor de las respectivas cuentas de las filas superiores, basta con multiplicar por 20 (por cada fila), el valor del recuento correspondiente en la primera fila.
El dispositivo presentaba 13 filas con 7 cuentas, 91 en total. Este fue un número básico para esta cultura. Tenía una estrecha relación con los fenómenos naturales, el inframundo y los ciclos de los cielos. Un Nepōhualtzintzin (91) representó el número de días que dura una estación del año, dos Nepōhualtzitzin (182) es el número de días del ciclo del maíz, desde su siembra hasta su cosecha, tres Nepōhualtzintzin (273) es el número de días de la gestación de un bebé, y cuatro Nepōhualtzintzin (364) completaron un ciclo y se aproximaron a un año. Cuando se tradujo a la aritmética informática moderna, el Nepōhualtzintzin ascendió al rango de 10 a 18 en punto flotante , que calculaba con precisión cantidades grandes y pequeñas, aunque no se permitía el redondeo.
El redescubrimiento del Nepōhualtzintzin se debió al ingeniero mexicano David Esparza Hidalgo, quien en sus viajes por México encontró diversos grabados y pinturas de este instrumento y reconstruyó varios de ellos en oro, jade, incrustaciones de concha, etc. Se atribuyen Nepōhualtzintzin muy antiguos. a la cultura olmeca , y algunas pulseras de origen maya , así como diversidad de formas y materiales en otras culturas.
Sánchez escribió en Aritmética en maya que se había encontrado otro ábaco de base 5, base 4 en la península de Yucatán que también computaba datos de calendario. Este era un ábaco de dedo, por un lado, se usaban 0, 1, 2, 3 y 4; y por otro lado se utilizaron 0, 1, 2 y 3. Tenga en cuenta el uso de cero al principio y al final de los dos ciclos.
El quipu de los incas era un sistema de cuerdas anudadas de colores que se usaban para registrar datos numéricos, como palos de conteo avanzados , pero que no se usaban para realizar cálculos. Los cálculos se realizaron utilizando una yupana ( quechua para "herramienta de contar"; ver figura) que todavía estaba en uso después de la conquista del Perú. Se desconoce el principio de funcionamiento de una yupana, pero en 2001 el matemático italiano De Pasquale propuso una explicación. Al comparar la forma de varias yupanas, los investigadores encontraron que los cálculos se basaban en la secuencia de Fibonacci 1, 1, 2, 3, 5 y potencias de 10, 20 y 40 como valores de lugar para los diferentes campos del instrumento. El uso de la secuencia de Fibonacci mantendría al mínimo el número de granos dentro de cualquier campo.
Rusia
El ábaco ruso, el schoty ( ruso : счёты , plural del ruso : счёт , contando), por lo general tiene una sola plataforma inclinada, con diez cuentas en cada alambre (excepto un alambre con cuatro cuentas para fracciones de cuarto de rublo ). Los modelos más antiguos tienen otro alambre de 4 cuentas para cuartos de kopeks , que se acuñaron hasta 1916. El ábaco ruso se usa a menudo verticalmente, con cada alambre en posición horizontal. Los alambres generalmente se arquean hacia arriba en el centro, para mantener las cuentas clavadas a ambos lados. Se borra cuando todas las cuentas se mueven hacia la derecha. Durante la manipulación, las cuentas se mueven hacia la izquierda. Para facilitar la visualización, las 2 cuentas del medio de cada cable (la quinta y la sexta cuenta) suelen ser de un color diferente de las otras ocho. Del mismo modo, el cordón izquierdo del alambre de miles (y el alambre de millón, si está presente) pueden tener un color diferente.
El ábaco ruso se usó en tiendas y mercados en toda la antigua Unión Soviética , y su uso se enseñó en la mayoría de las escuelas hasta la década de 1990. Incluso la invención de 1874 de la calculadora mecánica , el aritmómetro Odhner , no los había reemplazado en Rusia ; según Yakov Perelman . Se sabía que algunos hombres de negocios que intentaban importar calculadoras al Imperio Ruso se marchaban desesperados después de ver a un hábil operador de ábaco. Asimismo, la producción en masa de aritmómetros Felix desde 1924 no redujo significativamente el uso del ábaco en la Unión Soviética . El ábaco ruso comenzó a perder popularidad solo después de la producción en masa de microcalculadoras domésticas en 1974.
El ábaco ruso fue llevado a Francia alrededor de 1820 por el matemático Jean-Victor Poncelet , que había servido en el ejército de Napoleón y había sido prisionero de guerra en Rusia. El ábaco había dejado de utilizarse en Europa occidental en el siglo XVI con el auge de la notación decimal y los métodos algorítmicos . Para los contemporáneos franceses de Poncelet, era algo nuevo. Poncelet lo usó, no para ningún propósito aplicado, sino como una ayuda para la enseñanza y la demostración. Los turcos y los armenios usaban ábacos similares al schoty ruso. Fue nombrado coulba por los turcos y choreb por los armenios.
Ábaco de la escuela
En todo el mundo, los ábacos se han utilizado en preescolares y escuelas primarias como ayuda para enseñar el sistema numérico y la aritmética .
En los países occidentales, es común un marco de cuentas similar al ábaco ruso pero con alambres rectos y un marco vertical (ver imagen).
La estructura alámbrica se puede usar con notación posicional como otros ábacos (por lo tanto, la versión de 10 cables puede representar números hasta 9,999,999,999), o cada cuenta puede representar una unidad (por ejemplo, 74 se puede representar cambiando todas las cuentas en 7 cables y 4 cuentas en el octavo cable, por lo que se pueden representar números hasta 100). En el marco de cuentas que se muestra, el espacio entre el quinto y el sexto cable, correspondiente al cambio de color entre el quinto y el sexto cordón de cada cable, sugiere el último uso. La enseñanza de la multiplicación, por ejemplo, 6 por 7, puede representarse desplazando 7 cuentas en 6 alambres.
El ábaco rojo y blanco se utiliza en las escuelas primarias contemporáneas para una amplia gama de lecciones relacionadas con los números. La versión de veinte cuentas, a la que se hace referencia por su nombre holandés rekenrek ("marco de cálculo"), se utiliza a menudo, ya sea en una cadena de cuentas o en un marco rígido.
Feynman contra el ábaco
El físico Richard Feynman se destacó por su facilidad en los cálculos matemáticos. Escribió sobre un encuentro en Brasil con un experto en ábaco japonés, quien lo desafió a acelerar los concursos entre el lápiz y el papel de Feynman y el ábaco. El ábaco era mucho más rápido para la suma, algo más rápido para la multiplicación, pero Feynman era más rápido en la división. Cuando se utilizó el ábaco para un desafío realmente difícil, es decir, raíces cúbicas, Feynman ganó fácilmente. Sin embargo, el número elegido al azar estaba cerca de un número que Feynman sabía que era un cubo exacto, lo que le permitía usar métodos aproximados.
Análisis neurológico
Aprender a calcular con el ábaco puede mejorar la capacidad de cálculo mental. El cálculo mental basado en el ábaco (AMC), que se derivó del ábaco, es el acto de realizar cálculos, incluidas sumas, restas, multiplicaciones y divisiones, en la mente mediante la manipulación de un ábaco imaginario. Es una habilidad cognitiva de alto nivel que ejecuta cálculos con un algoritmo eficaz. Las personas que realizan entrenamiento AMC a largo plazo muestran una mayor capacidad de memoria numérica y experimentan vías neuronales conectadas de manera más efectiva. Son capaces de recuperar la memoria para hacer frente a procesos complejos. AMC implica un procesamiento visuoespacial y visuomotor que genera el ábaco visual y mueve las cuentas imaginarias. Dado que solo requiere que se recuerde la posición final de las cuentas, se necesita menos memoria y menos tiempo de cálculo.
Ábacos renacentistas
Ábaco binario
El ábaco binario se usa para explicar cómo las computadoras manipulan los números. El ábaco muestra cómo se pueden almacenar números, letras y signos en un sistema binario en una computadora o mediante ASCII . El dispositivo consta de una serie de cuentas en alambres paralelos dispuestos en tres filas separadas. Las cuentas representan un interruptor en la computadora en una posición de "encendido" o "apagado".
Usuarios con discapacidad visual
Un ábaco adaptado, inventado por Tim Cranmer, y llamado ábaco de Cranmer, es comúnmente utilizado por usuarios con discapacidad visual. Se coloca un trozo de tela suave o goma detrás de las cuentas, manteniéndolas en su lugar mientras los usuarios las manipulan. Luego, el dispositivo se utiliza para realizar las funciones matemáticas de multiplicación, división, suma, resta, raíz cuadrada y raíz cúbica.
Aunque los estudiantes ciegos se han beneficiado de las calculadoras parlantes, el ábaco a menudo se les enseña a estos estudiantes en los primeros grados. Los estudiantes ciegos también pueden completar tareas matemáticas usando un escritor braille y código Nemeth (un tipo de código braille para matemáticas) pero los problemas de multiplicación y división largas son tediosos. El ábaco les da a estos estudiantes una herramienta para calcular problemas matemáticos que iguala la velocidad y el conocimiento matemático requerido por sus compañeros videntes usando lápiz y papel. Muchas personas ciegas consideran que esta máquina numérica es una herramienta útil durante toda su vida.
Ver también
- Zhusuan chino
- Chisanbop
- Ábaco lógico
- Ábaco mental
- Huesos de Napier
- Mesa de arena
- Regla de cálculo
- Soroban
- Suanpan
Notas
Notas al pie
Referencias
- Aimi, Antonio; De Pasquale, Nicolino (2005). "Calculadoras Andinas" (PDF) . traducido por Del Bianco, Franca. Archivado (PDF) desde el original el 3 de mayo de 2015 . Consultado el 31 de julio de 2014 .
- Albree, Joe (2000). Hessenbruch, Arne (ed.). Guía del lector de historia de la ciencia . Londres, Reino Unido: Fitzroy Dearborn Publishers. ISBN 978-1-884964-29-9.
- Anon (12 de septiembre de 2002). "Edad media del ábaco, región de origen Oriente Medio" . Proyecto de Historia de la Computación . Archivado desde el original el 9 de mayo de 2014 . Consultado el 31 de julio de 2014 .
- Anon (2004). "Nepohualtzintzin, La computadora prehispánica" . Iberamia 2004 . Archivado desde el original el 3 de mayo de 2015 . Consultado el 31 de julio de 2014 .
- Anon (2013). 주판[Ábaco]. enc.daum.net (en coreano). Archivado desde el original el 7 de julio de 2012 . Consultado el 31 de julio de 2014 .
- Boyer, Carl B .; Merzbach, Uta C. (1991). Una historia de las matemáticas (2ª ed.). John Wiley & Sons, Inc. ISBN 978-0-471-54397-8.
- Brown, Lesley, ed. (1993). "ábaco" . Diccionario Oxford Inglés más corto sobre principios históricos . 2: AK (5ª ed.). Oxford, Reino Unido: Oxford University Press. ISBN 978-0-19-860575-1.
- Brown, Nancy Marie (2010). El ábaco y la cruz: la historia del Papa que llevó la luz de la ciencia a la Edad Media . Filadelfia, PA: Basic Books. ISBN 978-0-465-00950-3.
- Brown, Nancy Marie (2 de enero de 2011). "Todo lo que crees que sabes sobre la Edad Media es incorrecto" . rd magazine (Entrevista). USC Annenberg. Archivado desde el original el 8 de agosto de 2014.
- Burnett, Charles; Ryan, WF (1998). "Ábaco (occidental)". En Bud, Robert; Warner, Deborah Jean (eds.). Instrumentos de ciencia: una enciclopedia histórica . Enciclopedias Garland en la Historia de la Ciencia. Nueva York, NY: Garland Publishing, Inc. págs. 5-7. ISBN 978-0-8153-1561-2.
- Carr, Karen (2014). "Matemáticas de Asia occidental" . Kidipede . ¡Historia para niños !. Archivado desde el original el 3 de julio de 2014 . Consultado el 19 de junio de 2014 .
- Carruccio, Ettore (2006). Matemáticas y lógica en la historia y en el pensamiento contemporáneo . traducido por Quigly, Isabel. Transacción Aldine. ISBN 978-0-202-30850-0.
- Crump, Thomas (1992). El juego de los números japoneses: el uso y la comprensión de los números en el Japón moderno . Serie de estudios japoneses del Instituto Nissan / Routledge. Routledge. ISBN 978-0-415-05609-0.
- de Stefani, Aloysius, ed. (1909). Etymologicum Gudianum quod vocatur; recensuit et apparatum criticum indicesque adiecit . Yo . Leipzig, Alemania: Teubner. LCCN 23016143 .
- Fernandes, Luis (27 de noviembre de 2003). "Una breve introducción al ábaco" . ee.ryerson.ca . Archivado desde el original el 26 de diciembre de 2014 . Consultado el 31 de julio de 2014 .
- Flegg, Graham (1983). Números: su historia y significado . Libros de Dover sobre matemáticas. Mineola, NY: Publicaciones de Courier Dover. ISBN 978-0-233-97516-0.
- Gaisford, Thomas, ed. (1962) [1848]. Etymologicon Magnum seu verius Lexicon Saepissime vocabulorum origines indagans ex pluribus lexicis scholiastis et grammaticis anonymi cuiusdam opera concinnatum [ El gran Etymologicon: que contiene los orígenes del léxico de palabras de un gran número o más bien con una gran cantidad de investigación junto con Connexis Scholiastis por las Obras de Gramáticos Anónimos ] (en latín). Amsterdam, Países Bajos: Adolf M. Hakkert.
- Good Jr., Robert C. (otoño de 1985). "El ábaco binario: una herramienta útil para explicar las operaciones de la computadora". Revista de informática en la enseñanza de las matemáticas y las ciencias . 5 (1): 34–37.
- Gove, Philip Babcock, ed. (1976). "abacista". Tercer nuevo diccionario internacional de Websters (17ª ed.). Springfield, MA: G. & C. Merriam Company. ISBN 978-0-87779-101-0.
- Gullberg, Jan (1997). Matemáticas: desde el nacimiento de los números . Ilustrado por Pär Gullberg. Nueva York, NY: WW Norton & Company. ISBN 978-0-393-04002-9.
- Hidalgo, David Esparza (1977). Nepohualtzintzin: Computador Prehispánico en Vigencia [ El Nepohualtzintzin: Un eficaz Prehispánica Computer ] (en español). Tlacoquemécatl, México: Editorial Diana.
- Hudgins, Sharon (2004). El otro lado de Rusia: una parte de la vida en Siberia y el Lejano Oriente ruso . Eugenia & Hugh M. Stewart '26 Series sobre Europa del Este. Prensa de la Universidad de Texas A&M. ISBN 978-1-58544-404-5.
- Huehnergard, John, ed. (2011). "Apéndice de raíces semíticas, bajo la raíz ʾbq .". Diccionario de la herencia americana de la lengua inglesa (5ª ed.). Comercio de Houghton Mifflin Harcourt. ISBN 978-0-547-04101-8.
- Huff, Toby E. (1993). El ascenso de la ciencia moderna temprana: Islam, China y Occidente (1ª ed.). Cambridge, Reino Unido: Cambridge University Press. ISBN 978-0-521-43496-6.
- Ifrah, Georges (2001). La historia universal de la informática: del ábaco a la computadora cuántica . Nueva York, NY: John Wiley & Sons, Inc. ISBN 978-0-471-39671-0.
- Jami, Catherine (1998). "Ábaco (oriental)". En Bud, Robert; Warner, Deborah Jean (eds.). Instrumentos de la ciencia: una enciclopedia histórica . Nueva York, NY: Garland Publishing, Inc. ISBN 978-0-8153-1561-2.
- Klein, Ernest, ed. (1966). "ábaco". Un diccionario etimológico completo del idioma inglés . YO: AK. Amsterdam: Compañía editorial de Elsevier.
- Körner, Thomas William (1996). Los placeres de contar . Cambridge, Reino Unido: Cambridge University Press. ISBN 978-0-521-56823-4.
- Lasserre, Franciscus; Livadaras, Nicolaus, eds. (1976). Etymologicum Magnum Genuinum: Symeonis Etymologicum: Una Cum Magna Grammatica (en griego y latín). Primum: α - άμωσϒέπωϛ. Roma, Italia: Edizioni dell'Ateneo. LCCN 77467964 .
- Leushina, AM (1991). El desarrollo de conceptos matemáticos elementales en niños en edad preescolar . Consejo Nacional de Profesores de Matemáticas. ISBN 978-0-87353-299-0.
- Melville, Duncan J. (30 de mayo de 2001). "Cronología de las matemáticas mesopotámicas" . Universidad de St. Lawrence . It.stlawu.edu. Archivado desde el original el 12 de enero de 2014 . Consultado el 19 de junio de 2014 .
- Mish, Frederick C., ed. (2003). "ábaco" . Diccionario colegiado de Merriam-Webster (11ª ed.). Merriam-Webster, Inc. ISBN 978-0-87779-809-5.
- Mollin, Richard Anthony (septiembre de 1998). Teoría fundamental de números con aplicaciones . Matemáticas discretas y sus aplicaciones. Boca Raton, FL: CRC Press . ISBN 978-0-8493-3987-5.
- Murray, Geoffrey (20 de julio de 1982). "La calculadora antigua es un éxito con la generación más nueva de Japón" . El Monitor de la Ciencia Cristiana . CSMonitor.com. Archivado desde el original el 2 de diciembre de 2013 . Consultado el 31 de julio de 2014 .
- Cebollas, CT; Friedrichsen, GWS; Burchfield, RW, eds. (1967). "ábaco". El Diccionario Oxford de Etimología Inglesa . Oxford, Reino Unido: Oxford en Clarendon Press.
- Presley, Ike; D'Andrea, Frances Mary (2009). Tecnología de asistencia para estudiantes ciegos o con deficiencias visuales: una guía para la evaluación . Fundación Americana para Ciegos. pag. 61. ISBN 978-0-89128-890-9.
- Pullan, JM (1968). La historia del ábaco . Nueva York, NY: Frederick A. Praeger, Inc., Publishers. ISBN 978-0-09-089410-9. LCCN 72075113 .
- Reilly, Edwin D., ed. (2004). Enciclopedia Concisa de Ciencias de la Computación . Nueva York, NY: John Wiley and Sons, Inc. ISBN 978-0-470-09095-4.
- Sanyal, Amitava (6 de julio de 2008). "Aprendiendo por perlas". Tiempos del Hindustan .
- Smith, David Eugene (1958). Historia de las Matemáticas . Libros de Dover sobre matemáticas. 2: Temas especiales de matemáticas elementales. Publicaciones de Courier Dover. ISBN 978-0-486-20430-7.
- Stearns, Peter N .; Langer, William Leonard, eds. (2001). "La enciclopedia de la historia mundial: antigua, medieval y moderna, ordenada cronológicamente". La enciclopedia de la historia mundial (6ª ed.). Nueva York, NY: Houghton Mifflin Harcourt. ISBN 978-0-395-65237-4.
- Terlau, Terrie; Gissoni, Fred (marzo de 2005). "Ábaco = lápiz y papel al calcular" . Noticias APH . Imprenta americana para ciegos. Archivado desde el original el 2 de diciembre de 2013.
- Trogeman, Georg; Ernst, Wolfgang (2001). Trogeman, Georg; Nitussov, Alexander Y .; Ernst, Wolfgang (eds.). Informática en Rusia: se revela la historia de los dispositivos informáticos y la tecnología de la información . Braunschweig / Wiesbaden: Vieweg + Teubner Verlag. ISBN 978-3-528-05757-2.
- West, Jessica F. (2011). Rutinas de sentido numérico: desarrollo de la alfabetización numérica todos los días en los grados K-3 . Portland, Me .: Stenhouse Publishers. ISBN 978-1-57110-790-9.
- Williams, Michael R. (1997). Baltes, Cheryl (ed.). Una historia de la tecnología informática (2ª ed.). Los Alamitos, CA: IEEE Computer Society Press. ISBN 978-0-8186-7739-7. LCCN 96045232 .
- Yoke, Ho Peng (2000). Li, Qi y Shu: Introducción a la ciencia y la civilización en China . Libros de ciencia de Dover. Publicaciones de Courier Dover. ISBN 978-0-486-41445-4.
Leer
- Fernandes, Luis (2013). "El ábaco: una breve historia" . ee.ryerson.ca . Archivado desde el original el 2 de julio de 2014 . Consultado el 31 de julio de 2014 .
- Menninger, Karl W. (1969), Palabras numéricas y símbolos numéricos: una historia cultural de los números , MIT Press, ISBN 978-0-262-13040-0
- Kojima, Takashi (1954), El ábaco japonés: su uso y teoría , Tokio: Charles E. Tuttle Co., Inc., ISBN 978-0-8048-0278-9
- Kojima, Takashi (1963), Ábaco avanzado: teoría y práctica japonesas , Tokio: Charles E. Tuttle Co., Inc., ISBN 978-0-8048-0003-7
- Stephenson, Stephen Kent (7 de julio de 2010), Ancient Computers , IEEE Global History Network, arXiv : 1206.4349 , Bibcode : 2012arXiv1206.4349S , consultado el 2 de julio de 2011
- Stephenson, Stephen Kent (2013), Computadoras antiguas, Parte I - Redescubrimiento (2a ed.), ISBN 978-1-4909-6437-9
enlaces externos
-
 Textos en Wikisource:
Textos en Wikisource:
- " Ábaco ". Encyclopædia Britannica (11ª ed.). 1911.
- " Abacus ", de A Dictionary of Greek and Roman Antiquities , 3ª ed., 1890.
Tutoriales
- Heffelfinger, Totton & Gary Flom, Abacus: Mystery of the Bead - un manual de Abacus
- Mínimo multimedia
- Stephenson, Stephen Kent (2009), Cómo usar un ábaco de tablero de conteo